模型车轮胎侧偏刚度的参数辨识方法

李 玲，马 力，牟 宇，徐 超，李文茹，施树明

(吉林大学交通学院, 长春 130022)

模型车轮胎侧偏刚度的参数辨识方法

李 玲，马 力，牟 宇，徐 超，李文茹，施树明

(吉林大学交通学院, 长春 130022)

鉴于高速转弯等极限工况下，采用实车实验法研究车辆的稳定性存在极大的危险性，采用模型车代替实车进行车辆稳定性实验。研究车辆的动力学特性，须先获取轮胎参数，特别是轮胎的侧偏刚度。本文中首先基于2自由度车辆模型，推导了轮胎侧偏刚度的参数辨识模型，并采用低速圆周实验法测定了轮胎线性区域的侧偏刚度。然后，根据测得的轮胎侧偏刚度，一方面通过计算前轮转角并和利用Ackermann转向几何学得到的前轮转角进行对比，直接验证了参数辨识法测定轮胎侧偏刚度的准确性；另一方面通过计算轮胎魔术公式系数，间接验证了参数辨识法测定轮胎侧偏刚度的准确性。

2自由度车辆模型；侧偏刚度；参数辨识；Ackermann转向几何；轮胎魔术公式

前言

目前在汽车动力学领域，汽车操纵稳定性的理论发展已经相对成熟，并取得了很多好的理论成果。其中文献[1]中提出了以车身侧偏角和车身侧偏角变化率为变量的相平面分析方法，并确定了系统的带状稳定区域。文献[2]中利用李雅普诺夫第二方法，分析了直线行驶时，恒定速度下汽车的侧向稳定性。文献[3]中提出的引入纵向速度的3自由度模型，揭示了汽车操纵稳定性的本质特征是非线性动力学系统的混沌运动。文献[4]中为评价汽车安全辅助驾驶系统的有效性，提出了一种基于3自由度车辆模型的驾驶稳定区域的计算方法。文献[5]中在3自由度模型的基础上，引入驱动建立的5自由度模型，揭示了驱动对汽车操纵稳定性的影响。这些结论和成果为汽车操纵稳定性集成控制技术提供了动力学理论依据，但这些研究都只是限于理论分析，缺乏实验验证。

在高速转弯等极限工况下，采用实车实验法验证车辆的稳定性存在极大的危险性，因此考虑采用模型车代替实车进行车辆稳定性实验。轮胎侧偏刚度作为车辆动力学模型的基本参数，是进行模型仿真和车辆动力学分析的基础。因此，为研究车辆系统的动力学特性，开展车辆操纵稳定性实验分析和验证，首先需要获取轮胎侧偏刚度。

目前车辆轮胎侧偏刚度的获取主要通过2种方式：实验测定方法和参数估计法。由于轮胎实验台架等实验设备的购买和保养维修费用昂贵，因此有关轮胎侧偏刚度的估计方法应运而生。这些估计方法大体上可分为2类：侧偏角与侧偏刚度的联合估计和不含侧偏角的侧偏刚度估计法(又称beta-less方法)。

一种联合估计的方法是将侧偏角估计模型作为侧偏刚度估计器的一个输入量，同时将侧偏刚度的估计值用于更新车辆系统的线性模型[6]。文献[7]中采用GPS天线构建了类似结构的估计器。文献[8]中以某半钢子午线轮胎为研究对象，建立基于有限元软件 ABAQUS的复杂花纹轮胎侧偏特性分析有限元模型。基于显式有限元方法分析了不同侧偏角下轮胎侧向力的时间历程，获得该轮胎的侧偏刚度。文献[9]和文献[10]中提出一种EKF观测器实现对轮胎侧偏角和轮胎侧偏刚度的估计。这种联合估计方法由于其复杂性很难在汽车领域应用。因此，着重考虑不含侧偏角的侧偏刚度估计法，文献[11]中分别采用时域和频域法实现对轮胎侧偏刚度的有效估计，结果表明了beta-less方法在实施方面的巨大潜力。文献[12]中设计了一个滑模观测器来估计轮胎侧偏刚度。文献[13]中提出一种新的不包含轮胎侧偏角的侧偏刚度估计方法，该方法通过测定车辆左前轮和右前轮侧向力的差值来估计轮胎侧偏刚度。文献[14]中提出一种在线的轮胎侧偏刚度估计方法，该方法基于车辆系统2自由度线性模型，采用RLS方法估计得到前后轮的轮胎侧偏刚度。但这些方法计算过程复杂，通常会给估计器造成很大的负担。

基于上述研究，本文中为实现对模型车轮胎侧偏刚度的测定，基于2自由度车辆模型，推导了轮胎侧偏刚度的参数辨识模型，相应地设计了一种低速圆周运动实验。在测定模型车基本参数的基础上，采用GPS和INS相结合的方法获取车辆低速圆周运动的状态参数，利用参数辨识法辨识得到轮胎侧偏刚度。并分别通过前轮转角和魔术公式实现对测定的轮胎侧偏刚度准确性进行验证。

1 侧向-横摆联合法

假定左右轮胎侧偏角相等且前轮的转向角很小，并忽略侧倾运动，则可认为前后轴的左右轮胎分别被等价集中于车辆的前后轴与x轴的交点处，如图1所示。这样，一个四轮车辆被简化成了一个两轮车辆，使车辆运动分析变得更为简单。根据简化后的单轨车辆模型，本文中采用侧向-横摆联合法测定轮胎的侧偏刚度，采用车辆2自由度基本操纵模型[15]进行计算分析：

(1)

式中：m为模型车质量；a为前轴到质心的距离；b为后轴到质心的距离；Iz为绕z轴的转动惯量；Cf和Cr为前后轮侧偏刚度；δf为前轮转角；u为模型车纵向速度；v为模型车侧向速度；ω为横摆角速度。

图1 单轨车辆转向模型

因模型车前轮转角δf无法直接获取，故设法消去前轮转角。模型车4个车轮相同，即Cf=Cr。因此推导得到轮胎侧偏刚度的参数辨识模型：

Q=P·Cr

(2)

其中

(3)

式中：P为过程的输入量；Q为相应观测到的输出量；Cr为待辨识参数；L为轴距。

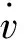
2 模型车基本参数的测定

采用在结构和性能上与实车相似的模型车作为实验车，该模型车型号为LosiMINIWRC1/5 4WD汽油动力拉力赛车，装备有29mL汽油发动机、频谱2.4GHz无线电系统和主动控制车辆(AVC)技术。该模型车采用四轮独立悬架，动力传动系统为具有三甲基硅油差速离心式离合器的4WD，轮胎类型为拉力TrekkA/T。

采用拉力计测定模型车的质量m。根据动量矩定理，采用实验法测定模型车的转动惯量。

(4)

式中：M为转矩；F为拉力。

图2 模型车转动惯量实验平台

实验得到的横摆角加速度与转动力矩的数据点如图3所示。采用最小二乘法计算得到对应的转动惯量Iz=2.41 kg·m2。模型车基本参数见表1。

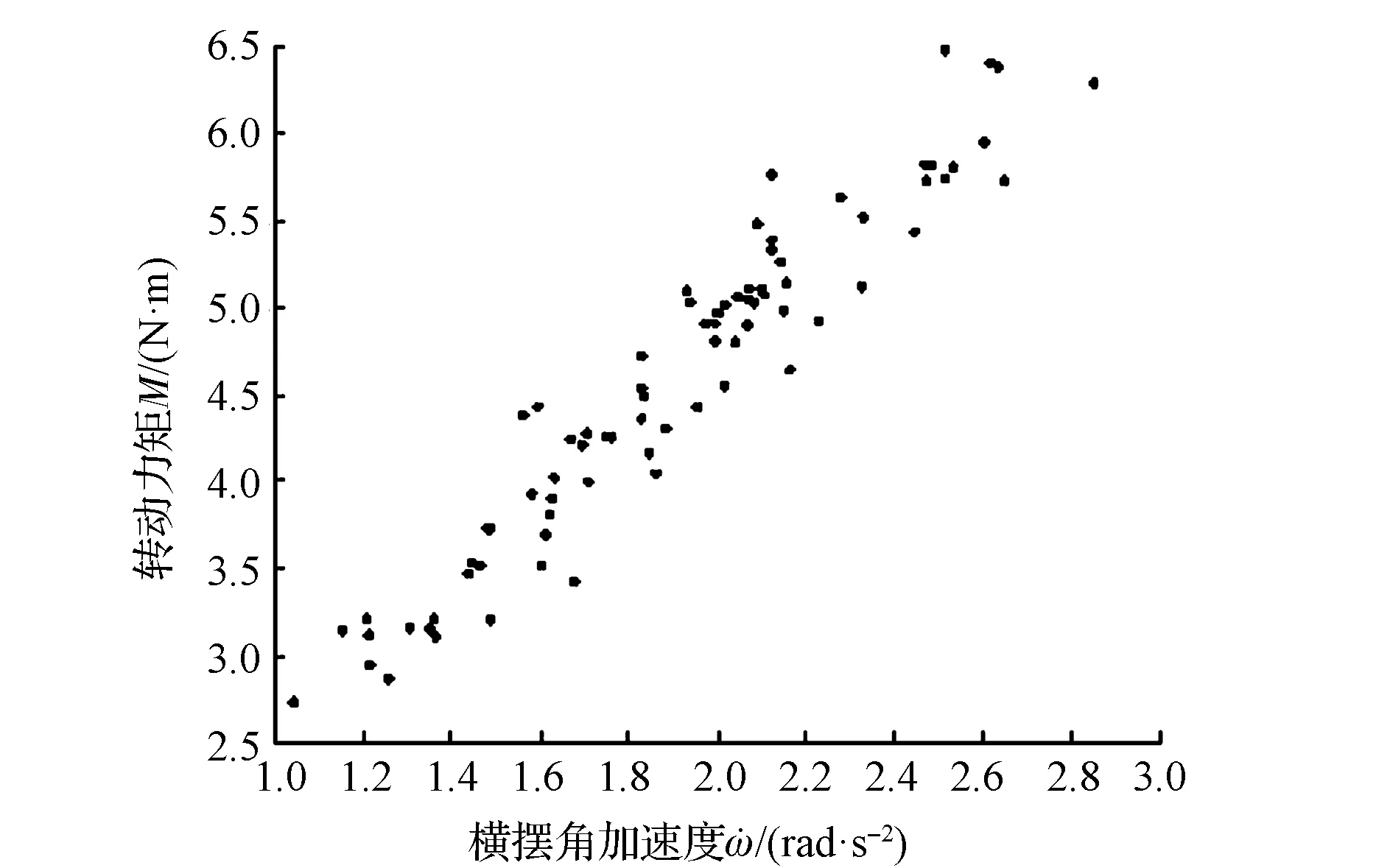
图3 横摆角加速度与转动力矩的数据点

表1 模型车基本参数

m/kga/mb/mL/mIz/(kg·m2)2243028033061241

3 实验法测定模型车状态变量

为获取模型车运行时的状态变量，进行低速圆周运动实验。为提高实验精度，采用了GPS差分系统。系统包括BDS/GPS双频卫星接收机XW-GNSS1060和MEMS惯性/卫星组合导航系统XW-GI-5651，能够实时获取车辆状态信息。实验场地如图4所示，实验路面为干燥的沥青路面。采用接收机XW-GNSS1060对试验场地所在地理位置进行标定后，模型车开始沿圆形试验场地(转盘)做低速圆周运动，转盘内径30m。差分基站接收机XW-GNSS1060安放位置如图5所示。导航系统XW-GI-5651和数据传输模块安装在模型车质心位置，前后天线分别固定在模型车的前后两端，如图6所示。利用车载导航系统XW-GI-5651实时采集模型车运动状态参数，数据采集频率为10Hz。导航系统XW-GI-5651采用RTK差分技术，能够在基站辅助下实时得到厘米级的定位精度。

图4 实验场地

图5 BDS/GPS双频卫星接收机XW-GNSS1060

图6 车载MEMS惯性/卫星组合导航系统XW-GI-5651

导航系统XW-GI-5651采集到的可利用数据包括：北向(X轴)速度和加速度、东向(Y轴)速度和加速度、绕Z轴的角速度、经纬度、偏航角和时间。这里X，Y和Z轴形成的坐标系为大地坐标系，偏航角以北向为0°(360°)，东向为90°，按顺时针方向计算。

模型车起始点的方向为北向，绕转盘逆时针行驶1圈后将测量得到的车辆的经纬度信息转化后得到车辆的运动轨迹图，如图7所示。在模型车逆时针行驶1圈的过程中，对应的车辆偏航角的变化如图8所示，图9为对应的北向速度Vn、东向速度Ve和车速V的变化。

图7 车辆的运动轨迹

由于导航系统XW-GI-5651采集的数据均是大地坐标系(X-O-Y)下的车辆状态参数，为得到车辆坐标系(x-o-y)下模型车实时运行的状态变量，须进行大地坐标系到车辆坐标系的坐标转换，如图10所示。

图8 模型车偏航角的时间序列

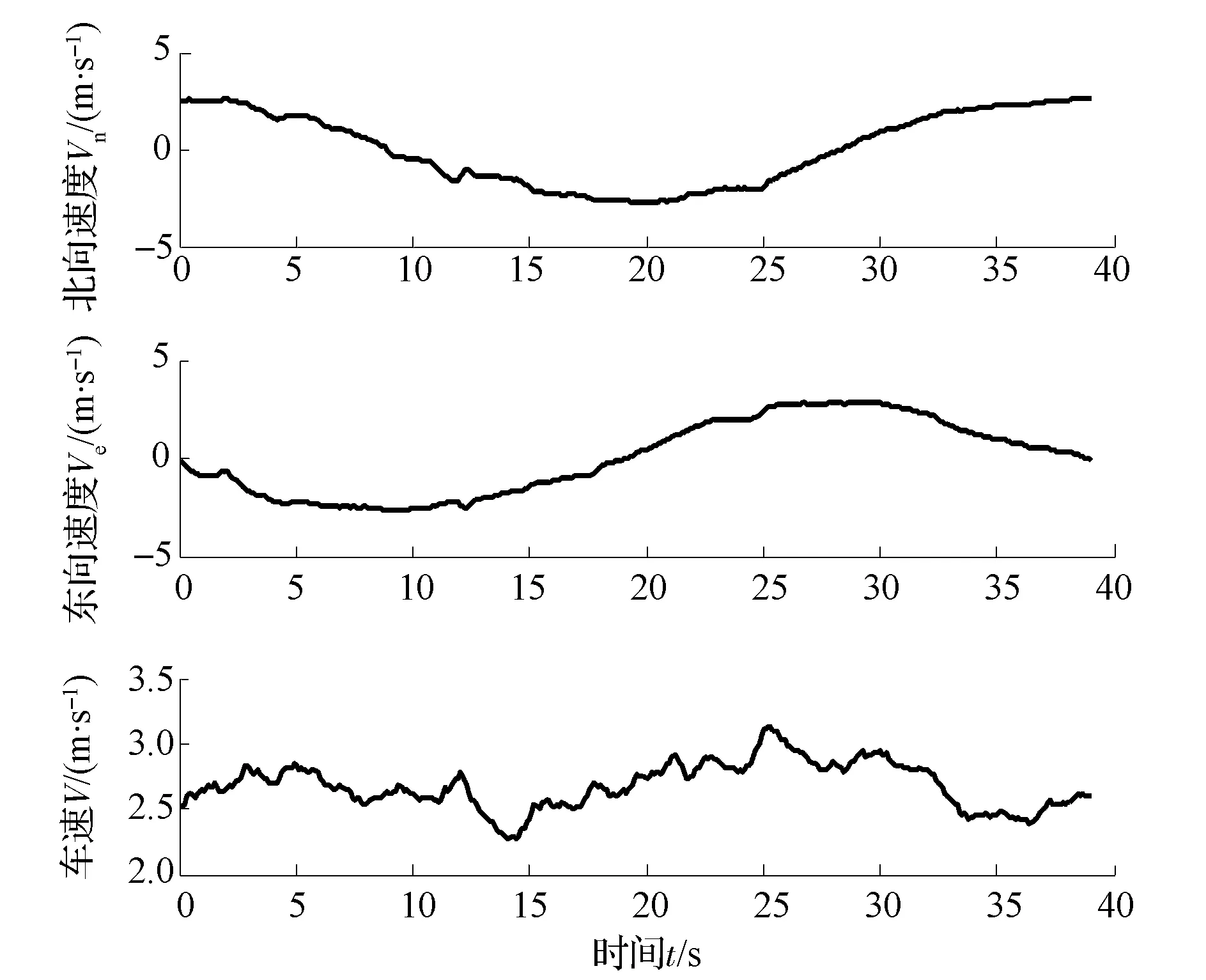
图9 模型车速度时间序列

图10 大地坐标系与车辆坐标系的转换

为得到车辆坐标系下模型车的纵向速度u和侧向速度v，需要知道模型车的横摆角ψ或质心侧偏角β。由于车辆的横摆角速度可以采集，因此考虑通过计算横摆角ψ实现车辆速度由大地坐标系向车辆坐标系的转换，且规定横摆角ψ以北向为0°(360°)，按逆时针方向计算。

实验中模型车起始点方向为北向，绕转盘逆时针行驶1圈。由图10可知，在整个行驶过程中，车辆的横摆角ψ、质心侧偏角β和偏航角φ3个角度之间存在如下关系：

ψ=2π-β-φ

(5)

因起始点时车辆的质心侧偏角很小，故假设β0=0，车辆的初始横摆角ψ0=2π-φ0。采用车辆横摆角速度求积分的方法计算整个行驶过程中车辆的横摆角ψ和车辆坐标系下模型车的纵、侧向速度u和v：

(6)

(7)

图11为与图8对应的模型车横摆角时间序列，图12为模型车横摆角速度时间序列和计算得到的纵、侧向速度时间序列。

图11 模型车横摆角的时间序列

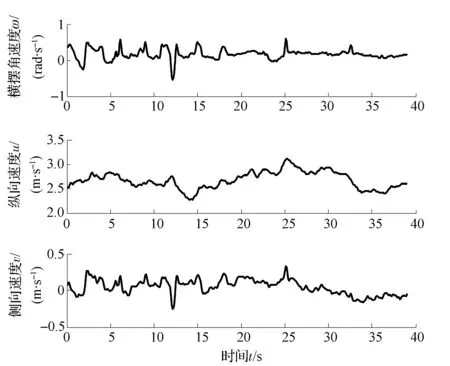
图12 模型车状态变量时间序列

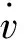
(8)

4 参数辨识法确定轮胎侧偏刚度

按照上述实验方案进行20次低速圆周运动，即模型车逆时针绕转盘行驶20圈。结合第2节测定的车辆基本参数和第3节获取的车辆运行时的各状态变量，采用参数辨识的方法确定轮胎侧偏刚度。

由式(2)可知待辨识的参数为Cr，采用准则函数：

J=∑(Q-P·Cr)2

(9)

利用最小二乘法求J的最小值Jmin，即求J对Cr的偏导数并令其为0：

(10)

整理后得

(11)

令BQ=∑Q，AP=∑P，20次实验结果得到的AP和BQ散点图如图13所示。最终得到的后轮侧偏刚度为Cr=1.5499kN/rad。

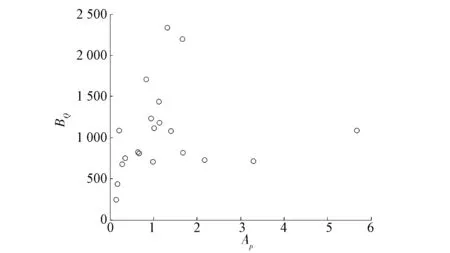
图13 实验得到的AP和BQ数据点

5 轮胎侧偏刚度的准确性验证

5.1 通过前轮转角验证轮胎侧偏刚度

由于模型车前轮转角无法采用车载系统直接获取，这里采用车辆2自由度基本操纵模型推导得到前轮转角的动力学公式：

(12)

将第4节得到的轮胎侧偏刚度作为已知参数代入式(12)，计算前轮转角δf1。通过验证计算得到的前轮转角δf1的准确性来实现对轮胎侧偏刚度的准确性检验。

模型车在车速较低的情况下几乎不涉及车辆的动态响应问题，车辆的运动简单地服从所谓“Ackermann几何关系”。即汽车轨迹曲率ρ与前轮转角δf成正比，因此前轮转角可采用式(13)计算[16]：

δf≈L/R=Lρ

(13)

其中车辆的转向半径为R，轨迹曲率ρ可根据图7中的车辆运动轨迹和图8中偏航角的变化采用式(14)计算：

(14)

图14对比了一次实验中采用车辆2自由度模型得到的前轮转角和通过Ackermann转向几何学得到的前轮转角，图15为其对应的差值。由图可知，除了个别的异常点外，通过车辆2自由度模型的动力学公式计算得到的前轮转角δf1与通过Ackermann转向几何关系计算得到的前轮转角δf相对接近，从而验证了上述轮胎侧偏刚度的准确性。

图14 前轮转角时间序列

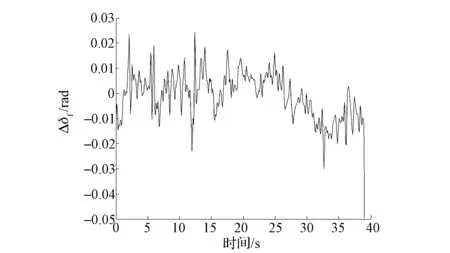
图15 两种方法得到的前轮转角的差值

5.2 利用魔术公式验证轮胎侧偏刚度的准确性

为进一步验证轮胎侧偏刚度的准确性，将轮胎侧偏刚度引入由文献[17]提出的“魔术公式”轮胎模型中。通过计算魔术公式的参数，验证轮胎侧偏刚度的准确性。

“魔术公式”是以三角函数组合的形式来拟合轮胎实验数据，得出了一套形式相同并可同时表达纵向力、侧向力和回正力矩的轮胎模型，其形式为

y=Dsin(Carctan(Bx-E(Bx-arctanBx)))

(15)

“魔术公式”中的系数由图16说明，图中所示的曲线可以是纵向力、侧向力或回正力矩关系曲线[18-19]。其中，D=yp为曲线峰值(C≥1时)；C为曲线形状系数，它控制了“魔术公式”中正弦函数的范围，决定了所得曲线的形状，其值可由曲线峰值yp以及稳定值ys决定，其计算式如式(16)所示。系数B，C和D的乘积对应于曲线在原点(x=y=0)处的斜率，即BCD=tanθ；当C和D决定后，即可根据式(17)求得刚度系数B；系数E用来控制曲线峰值处的曲率，其计算式如式(18)所示，其中滑移曲线在纵侧向滑移范围内达到峰值的位置xp可用式(19)计算[20-21]。

(16)

(17)

(18)

(19)

图16 “魔术公式”中各参数的轮胎特性曲线

(20)

(21)

表2 轮胎参数取值

将表2中的参数分别代入式(15)魔术公式，计算得到的前后轮侧偏角和侧向力如图17所示。该仿真结果符合“魔术公式”的正弦曲线形状，且模型车前轮侧向力在侧偏角为9.2°时达到峰值，后轮侧向力在侧偏角为8°时达到峰值，验证了轮胎侧偏刚度的准确性。

图17 模型车前后轮侧向力与侧偏角拟合结果

6 结论

为测定1/5模型车的轮胎侧偏刚度，本文中设计了低速圆周运动实验。首先搭建模型车转动实验台测定模型车的基本参数，然后采用GPS和INS相结合的方法实现车辆运动参数的测定，根据侧向横摆联合法和参数辨识法，测得轮胎侧偏刚度为1.549 9kN/rad。并分别通过前轮转角和魔术公式验证实验得到的轮胎侧偏刚度的准确性。结果表明，采用低速圆周实验法和参数辨识法能准确方便地实现对模型车轮胎侧偏刚度的测定，为极限工况下车辆操纵稳定性的实验验证提供支持。

[1] INAGAKI S, KUSHIRO I, YAMAMOTO M. Analysis on vehicle stability in critical cornering using phase-plane method[C]. SAE Paper 9438411.

[2] JOHNSON D B, HUSTON J C. Nonlinear lateral stability analysis of road vehicles using Lyapunov’s second method[C]. SAE Paper 841057.

[3] 刘丽. 车辆三自由度平面运动稳定性的非线性分析及控制策略评价[D].长春：吉林大学，2010.

[4] HORIUCHI Shinichiro. Evaluation of chassis control method through optimisation-based controllability region computation [J]. Vehicle System Dynamics，2012,50(2):19-31.

[5] WANG Xianbin, SHI Shuming, LIU Li, et al. Analysis of driving mode effect on vehicle stability[J]. International Journal of Automotive Technology, 2013, 14(3): 363-373.

[6] FUJIMOTO H, TAKAHASHI N, TSUMASAKA A, et al. Motion control of electric vehicle based on cornering stiffness estimation with yaw-moment observer[C].Advanced Motion Control, 2006. 9th IEEE International Workshop on. IEEE, 2006: 206-211.

[7] ANDERSON R, BEVLY D M. Estimation of tire cornering stiffness using GPS to improve model based estimation of vehicle states[C].Intelligent Vehicles Symposium, 2005. Proceedings. IEEE. IEEE, 2005: 801-806.

[8] 姜明磊, 周涛, 叶树斌, 等. 轮胎侧偏刚度有限元仿真研究[J]. 机械设计与制造工程, 2015, 44(9): 15-19.

[9] BAFFET G, CHARARA A, LECHNER D. Estimation of vehicle sideslip, tire force and wheel cornering stiffness[J]. Control Engineering Practice, 2009, 17(11): 1255-1264.

[10] BAFFET G, CHARARA A, LECHNER D, et al. Experimental evaluation of observers for tire-road forces, sideslip angle and wheel cornering stiffness[J]. Vehicle System Dynamics, 2008, 46(6): 501-520.

[11] SIERRA C, TSENG E, JAIN A, et al. Cornering stiffness estimation based on vehicle lateral dynamics[J]. Vehicle System Dynamics, 2006, 44(sup1): 24-38.

[12] WANG R, WANG J. Tire-road friction coefficient and tire cornering stiffness estimation based on longitudinal tire force difference generation[J]. Control Engineering Practice, 2013, 21(1): 65-75.

[13] NGUYEN B M, NAM K, FUJIMOTO H, et al. Proposal of cornering stiffness estimation without vehicle side slip angle using lateral force sensor[J]. IIC, 2011, 11: 140.

[14] LEI Z, YU L, NING P, et al. Vehicle direct yaw moment control based on tire cornering stiffness estimation[C].ASME 2014 Dynamic Systems and Control Conference. 2014: V003T49A004.

[15] 喻凡, 林逸. 汽车系统动力学[M]. 北京：机械工业出版社, 2005.

[16] 郭孔辉.汽车操纵动力学[M]. 长春：吉林科学技术出版社, 1991.

[17] PACEJKA H. Tire and vehicle dynamics[M]. Elsevier, 2005.

[18] BRAGHIN F, SABBIONI E. A dynamic tire model for ABS maneuver simulations[J]. Tire Science and Technology, 2010, 38(2): 137-154.

[19] SCHMID MARKUS. Tire modeling for multibody dynamics applications[D].Madison:University of Wisconsin-Madison, 2011.

[20] Automotive TNO. MF-Tyre/MF-Swift 6.1.1 Help manual[M]. TNO Automotive, The Netherlands, 2009.

[21] Automotive TNO. Tyre models user manual[M]. Using the MF-MC Tyre Model (May 2002), 2002.

Parameter Identification Method for the Tire Cornering Stiffness of Model Vehicle

Li Ling, Ma Li, Mu Yu, Xu Chao, Li Wenru & Shi Shuming

TrafficCollege,JilinUniversity,Changchun130022

In view of the high danger when conducting real vehicle test to study vehicle stability in extreme condition such as high-speed turn, model vehicle is used instead to perform stability experiment. The study on the dynamic characteristics of vehicle requires tire parameters, in particular, tire cornering stiffness to be know in advance. In this paper, firstly a parameter identification model for tire cornering stiffness is derived based on 2 DOF vehicle model, and the tire cornering stiffness in linear segment is measured by low-speed circle test. Then according to the tire cornering stiffness measured, the turning angle of front wheel is calculated and compared with that determined by Ackermann steering geometry, so directly verifying the measurement correctness of cornering stiffness by parameter identification on one hand; while the coefficients in tire magic formulae are calculated, with the measurement correctness of cornering stiffness by parameter identification indirectly verified on the other hand.

2 DOF vehicle model; tire cornering stiffness; parameter identification; Ackermann steering geometry; tire magic formula

*国家自然科学基金(51475199)资助。

2016238

原稿收到日期为2016年4月12日。