整车风洞射流对声传播路径影响的试验研究*

沈 哲，王毅刚，杨志刚，李方旭

(1.同济大学汽车学院，上海 201804； 2.同济大学，上海地面交通工具风洞中心，上海 201804)

整车风洞射流对声传播路径影响的试验研究*

沈 哲，王毅刚，杨志刚，李方旭

(1.同济大学汽车学院，上海 201804； 2.同济大学，上海地面交通工具风洞中心，上海 201804)

对整车风洞射流结构对声传播路径的影响进行了试验研究。设计了翼型音箱，用传声器阵列进行声源定位，测量了全尺寸3/4开口式风洞中多种参数条件下的声漂移量。结果表明，射流速度和声源位置的影响较大，而声源的种类与高度和测量点位置的影响可以忽略。用试验数据拟合出了整车声学风洞中声漂移量的预测公式并验证了其精度和适用范围。

风洞；射流；声漂移;传声器阵列

前言

射流是流体由于压力差等原因，从喷口射出，与喷口外相对静止的流体急剧混合的流动。射流结构包括：在喷口下游一定区域形成与喷口内速度基本相等的势流核心区；不受射流影响的静止流体区；在核心区与静止区之间有速度梯度的剪切层区。

开口式整车声学风洞中气流从喷口进入测试段的过程是典型的射流。射流结构的存在使得声从流场内向流场外传播的过程变得复杂，声传播路径发生改变。近年来传声器阵列声源识别系统的技术发展很快，在整车气动声学风洞试验中也逐渐普及，成为风洞中对整车外气动噪声测试的重要技术手段。传声器阵列测量必须在流场外静止区进行，由于射流结构的存在，流场外测量无法对声源准确定位，是准确了解噪声源进而进一步优化的重要技术障碍。

国外很早就开始对射流中的声传播问题进行研究，其中比较有影响的是利用几何声学原理，研究流体对声的折射影响[1-5]。而这类研究主要针对航空气动声学中出现的问题，试验也是在对航空问题进行研究的小尺寸(喷口面积1～2m2)全开口式声学风洞中进行的[4-6]。国际上主流的整车气动声学风洞，如同济大学、斯图加特大学、奥迪公司等气动声学风洞的喷口面积均在10m2以上，且为带有地面的3/4开口式，与航空风洞差别较大，因此有必要对汽车风洞的声传播问题进行研究和验证。

本文中主要通过试验的方法对整车声学风洞中的声漂移量进行研究。设计对射流流动影响极小的翼型音箱，控制流场内产生的声源，用相位传声器阵列进行声源定位，获得声源由于射流结构产生的声漂移量。试验结果表明，声漂移主要受射流速度和声源在风洞平面内的几何位置影响，并给出应用于开口式大尺寸低速风洞中预测声漂移的公式。

1 风洞中的声漂移

本文中研究声传播路径变化是通过如图1所示声源识别设备测量得到的声源位置与实际声源位置即喇叭所在的位置的坐标差，得到声源位置由于射流结构存在而产生的变化量，即声漂移量d。

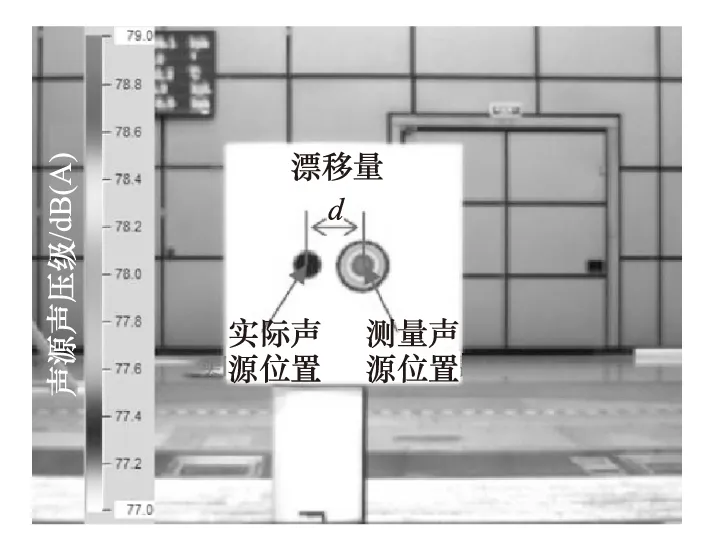
图1 由于射流结构产生的声漂移现象

1.1 射流中的声传播

参照传统的几何声学[4-5]，将声传播的方向用波阵面的法线表示，剪切层简化为无限薄后，风洞射流内的声波向流场外传播的过程如图2所示。

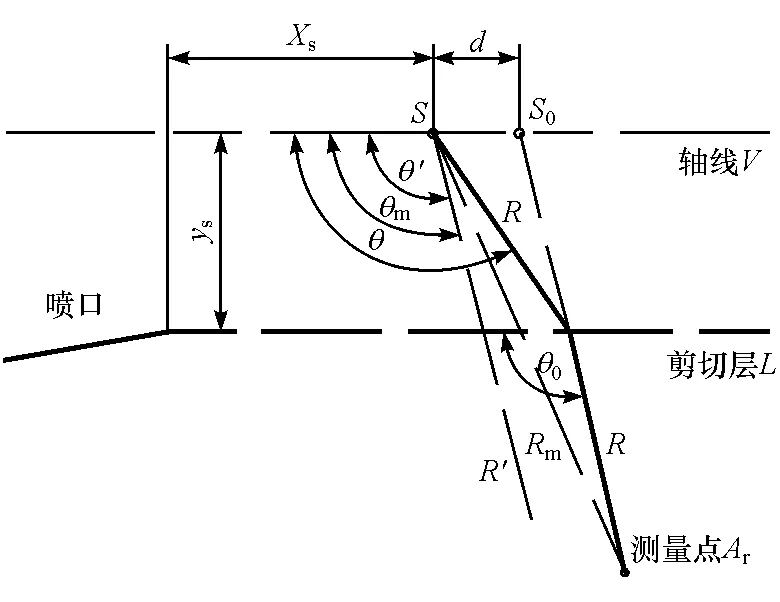
图2 射流中声传播的基本模型

图中：S表示实际声源，S0表示测量点处观测到的假定声源，S至S0的距离即为声漂移量d；Ar表示测量点；V表示经过声源S并与喷口平面垂直的一条直线，在此模型中认为剪切层L与V平行；xs表示声源到喷口的距离，ys表示声源到剪切层的距离；R′表示声在静止空气中传播经过的路径，θ′表示R′与V的夹角；R表示声实际传播经过的路径，在流场内，由于射流的存在，声的传播方向会向射流的流动方向偏转一定的角度，θ表示R在流场内与V的夹角；声经过剪切层时，由于剪切层的作用会产生折射，θ0表示R在流场外与V的夹角；Rm表示实际声源S与测量点Ar的连线，θm表示Rm和V的夹角。

1.2 几何声学求解声漂移

传统的几何声学的理论对射流中声传播的求解如下[4]。

势流核心区中由于波对流产生的从θ′到θ的偏转关系为

(1)

式中M为射流的马赫数。

声通过剪切层时折射产生的θ0和θ′的Snell声折射定理关系为

(2)

式中c0和ct分别为剪切层内外的声速，在本场合，c0/ct=1。

其他几何关系有

Rmcosθm=yscotθ+(Rmsinθm-ys)cotθ0

(3)

dsinθ0=Rmsin(θm-θ0)

(4)

联立式(1)～式(4)即可求解漂移量d，其中M，Rm，θm，ys和θ′为已知的输入条件。

以上几何声学的理论虽然在一定程度上解决了射流中声传播路径的问题，但由于这部分的研究进行得较早，并且都是在小尺寸航空声学中进行试验验证，因而在整车声学风洞中应用有较多的局限性：

(1) 之前研究的马赫数较高，一般在0.2～0.7，而整车试验风速一般不超过300km/h，即马赫数小于0.3；

(2) 3/4开口结构的整车风洞的地面对声传播路径是否影响未进行研究；

(3) 早期的主要研究都没有考虑剪切层的厚度随着射流轴向距离xs的变化对声传播路径影响的差异，而类似本研究中的整车风洞尺寸较大，在常规的测试位置即距喷口5m左右，剪切层厚度已超过0.4m，大于1 000Hz声的波长，剪切层厚度的影响必须考虑；

(4) 最重要的一点是，上述式(1)～式(4)方程组在θm=θ′=90°时是无解的，并且在θm和θ′接近90°时解的误差也很大，而整车声学试验中，传声器阵列一般都是正对测量目标，即θm≈90°，此情况下用几何声学求解出来的声漂移量与实际测量值相差很大。

综上所述，几何声学在整车声学风洞中预测传声器阵列测量得到的声漂移量的局限性较大，其方法还有待进一步发展。而声漂移的确定是风洞试验迫切需要解决的问题，因此本文中采用试验的方法研究声漂移量与各个参数的关系。

2 试验研究

2.1 声源设计

为了试验研究风洞中的声传播，需要在风洞势流核心区安置一个声源，该声源需满足如下条件：(1)声源表面流动的速度梯度要尽量小；(2)放入流场后对流场影响比较小；(3)为简化之后的研究，流动在一定的高度范围内呈二维相似；(4)自身低气动噪声；(5)产生的声信号可控；(6)在高度方向可调整。

为满足上述条件，采用了喇叭外加导流罩的翼型音箱，外接功放和信号源组成试验所需的声源。

此声源的设计难点在于翼型音箱的导流罩外形设计，在设计导流罩的过程中，以数值仿真为主要手段，围绕上述(1)～(4)点的要求，反复设计优化导流罩的外形，最终确定如图3所示的导流罩外形。

图3 导流罩表面附近流线分布

该导流罩采用NACA0008对称翼型为基础，通过沿高度方向z拉伸、修角、倒圆、截尾等方法形成，翼型音箱部分长1 000mm，宽96mm，高1 000mm，喇叭安装在前后方向x离头部280mm，高度z为对称中心处；翼型柱支撑件为分段式，可调声源的高度。

图中的线条为距表面10mm截面流线数值仿真结果，为了更清晰地显示，仅画出喇叭(高度中心位置)及以下部分的流线，可以看到导流罩尤其是喇叭口附近流线非常平顺。从以上数值仿真结果看，此导流罩能满足声源设计要求。

2.2 风洞试验平台、测试设备

试验在同济大学上海地面交通工具风洞中心整车气动声学风洞中完成。该风洞是3/4开口回流风洞；喷口尺寸(宽×高)为6.5m×4.25m；驻室尺寸为22m×17m×12m。试验最大风速可达250km/h，试验段自由场空间的低频截止频率为50Hz，在160km/h风速下背景噪声低于61dB(A)，静压梯度小于0.001/m。

试验所用声源为HEAD Acoustics Artemis软件生成的各种标准声信号，通过电脑回放，经B&K 2716功放后在翼型音箱发出的声信号。

试验中采用的测量设备为德国Gfai公司的相位传声器阵列声源识别系统，如图4所示，其具体参数如下：阵列，适合于整车气动声学风洞流场外进行声源识别的平面螺旋形阵列，尺寸为1.8m×1.8m；传感器，GRAS公司1/4英寸阵列专用压力型传声器，120套；数采系统，120通道高精度数采，单通道采样率192kHz；软件系统，基于波束成型算法的声源识别软件NoiseImage。

图4 相位传声器阵列声源识别系统

2.3 试验内容和试验方法

试验中主要研究的内容为射流结构特性、声源信号的种类和所处的位置对整个声传播过程的影响。为此，在试验中改变喷口射流速度和声源信号的频率成分、强度、位置与测量点的位置，获得相应结果。

图5为试验中声源和阵列的几何位置示意图，声源3个位置分别为A(3.9，2.7)，B(3.9，4)和C(5.5，2.7)，括号内坐标为到喷口下角的距离，即(xs，ys)。阵列位置有中心正对声源和向y+方向移动1m两种。阵列始终与喷口轴线保持平行。

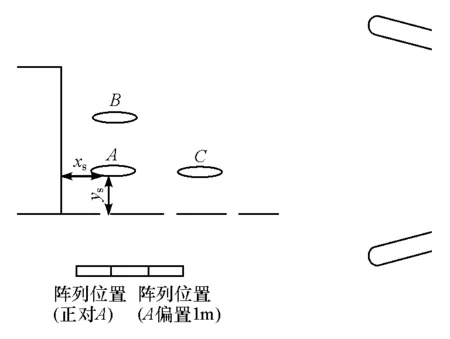
图5 声源和传声器阵列在风洞中的位置

本文中除有指明外，测试条件均为声源位于A点，高度1.1m，阵列正对声源。

3 试验结果和分析

3.1 不同声信号的影响

试验时测量了多种声信号，包括了按1/3倍频程给出200～5 000Hz的纯音信号、以1kHz为中心频率的宽频噪声以及频率范围为10Hz～20kHz的白噪声信号。

处理测试结果时发现，测量频率越高，声漂移量的稳定性越好。对于低于800Hz声信号源的位置识别结果精度较差，计算出来的声源覆盖范围大、中心位置与实际偏差较大。分析原因有如下两点：(1)由于低频声的波长较大，所以对低频信号的识别精度较差；(2)在气流中翼型音箱后部由涡脱落产生的气动噪声的频率也在低频，这部分气动声与喇叭、箱体产生的声位置很接近，混合在一起产生了更大的区域声源。因此之后都只给出800Hz以上频率的结果。

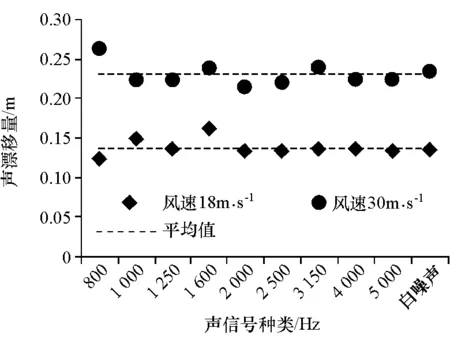
图6 18和30m/s两种风速下不同频率单频声信号的漂移量

图6为18和30m/s两种风速下，按1/3倍频程给出800～5 000Hz不同频率单频声信号的漂移量，包含白噪声的漂移量作为参考。结果显示，不同频率信号漂移量虽然有一定的上下波动，且低频部分的波动范围大一些，但始终围绕在平均值附近，可以认为波动主要是测量误差，不同频率信号对声漂移量没有直接的影响。

图7为18和30m/s两种风速下，以1kHz为中心频率，逐渐加宽频率带的范围的声信号(1 000Hz纯音、900～1 111Hz，800～1 250Hz和700～1 428Hz)的漂移量，包含白噪声和粉红噪声的漂移量作为参考。结果显示，不同带宽信号漂移量虽然有一定的上下波动，但始终围绕在平均值附近，可以认为波动主要是测量误差，不同带宽信号对声漂移量没有直接的影响。

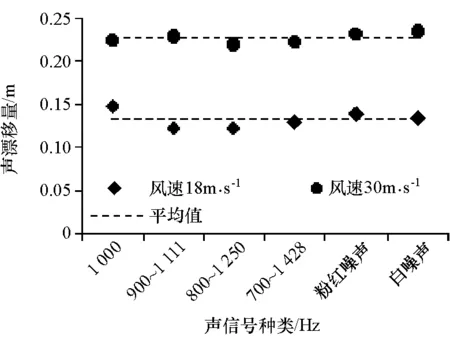
图7 18和30m/s两种风速下不同频率宽度声信号的漂移量

综上所述，漂移量与声频率高低和频带的宽度没有直接的关系，这与之前的研究结果相符[5]。

3.2 声源高度的影响

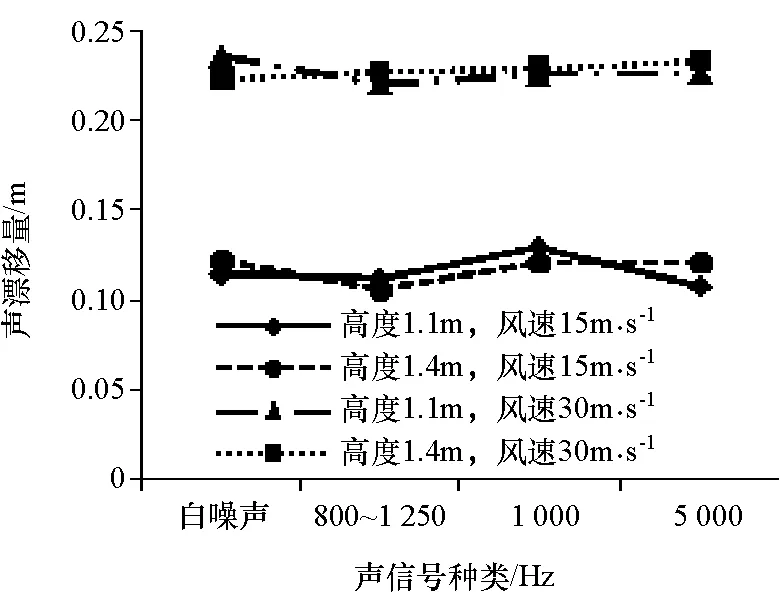
图8 1.1和1.4m两种高度下15和30m/s两种风速声漂移量

整车风洞的地面是与全开口航空风洞较为不同的地方，本文中通过改变声源高度研究地面是否对声漂移量有影响，图8为两种不同声源高度在两种风速下4种声信号的漂移量，从结果看两种声源高度的漂移量始终非常接近，声源高度对声漂移量没有明显的影响，进而得到在离地面一定高度以上，声漂移量不受地面的影响。

3.3 射流速度的影响

射流速度对声漂移量的影响最直接，图9和图10分别给出不同射流速度下1kHz纯音、白噪声两种声信号声漂移量。

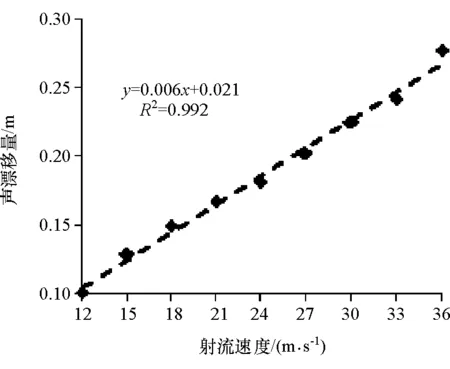
图9 1kHz纯音声漂移量随射流速度的变化

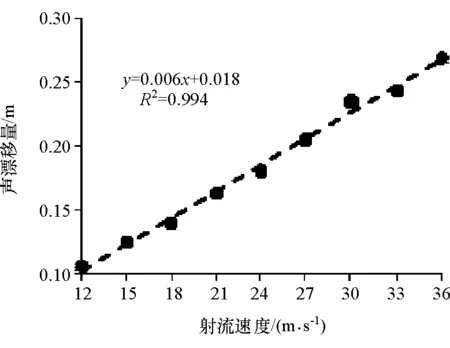
图10 白噪声漂移量随射流速度的变化

由图9和图10可见：声漂移量d与射流速度U线性拟合的R2值都大于0.99，说明两者呈线性关系；且两种声信号斜率基本相同，余项值也非常小，进一步验证了第3.1节中声信号种类对漂移量没有直接影响的结论。

3.4 几何位置的影响

(1) 测量点位置

图11为正对声源和偏置两种阵列位置测量的两种风速下4种声信号的漂移量。结果显示，两种阵列位置的结果始终非常接近，可以认为这两种测量点的位置对声漂移量基本没有影响。从原理上，声阵列测量的是一个范围内接受的声信号，只要声传播方向还在阵列的测量范围内，漂移量就不会变化。

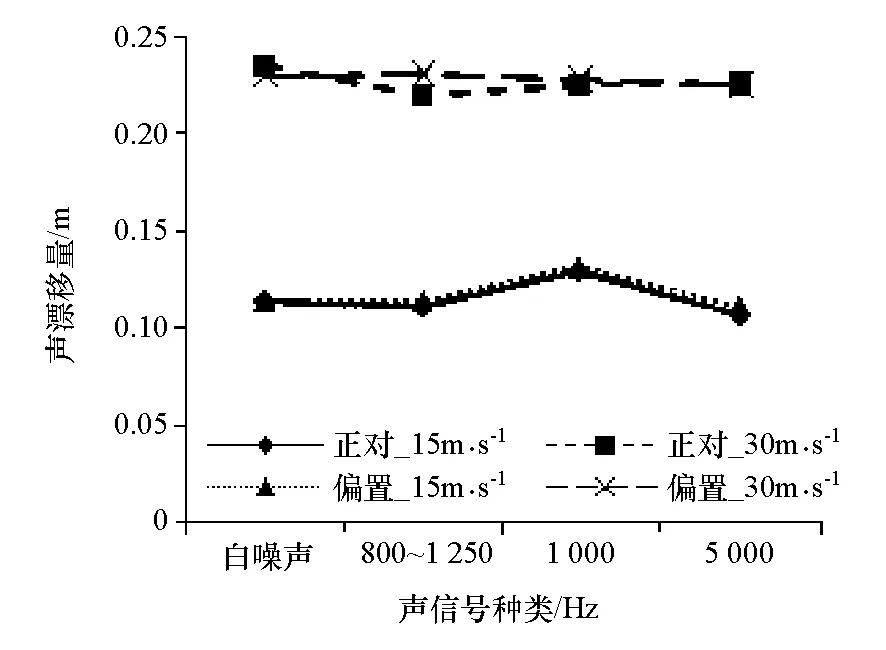
图11 两种风速下阵列不同位置对漂移量的影响

(2) 射流中传播距离

从第1.2节可知，由于波对流效应，声在势流核心区经过的距离越长，声波阵面偏转的距离就越大。图12为声源在射流中不同传播距离ys的两个声源位置A和B在两种风速下两种声信号的漂移量。

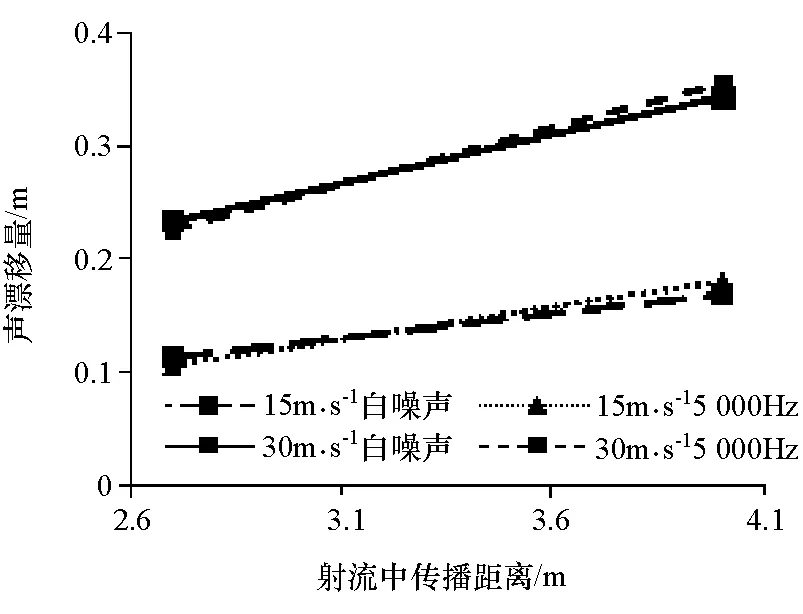
图12 射流中传播距离ys对漂移量的影响

结果显示随着ys的增大，声漂移量d也明显增大。经计算，ys与d基本成正比。

(3) 轴向位置

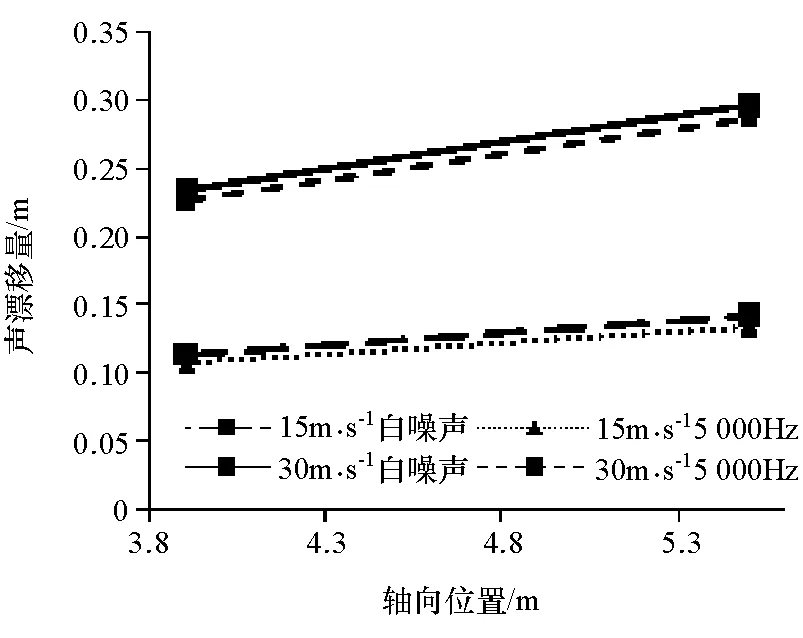
图13 轴向位置xs对漂移量的影响

射流中剪切层的厚度与轴向位置xs接近成正比[7]，剪切层厚度影响声折射的角度，继而对漂移量产生影响。图13为声源在射流中不同传播距离xs的两个声源位置A和C在两种风速下两种声信号的漂移量。

结果显示，随着xs的增大，声漂移量d也明显增加，两者呈线性关系，但不成正比。

4 声漂移预测公式

第3节的结果显示，U，ys和xs对漂移量d都有影响，本节根据A，B和C3个测试位置的结果，拟合出d与U，ys和xs之间的关系。

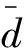
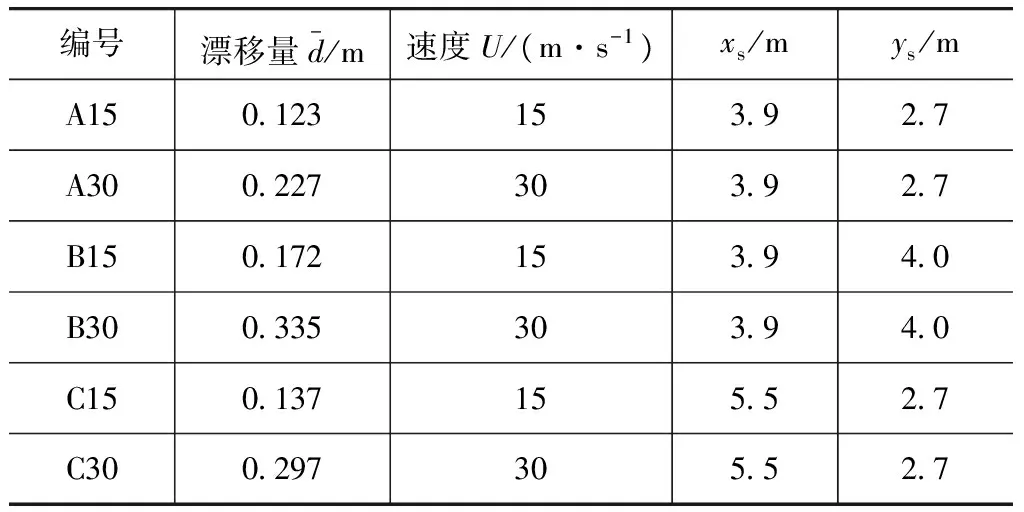
表1 漂移量与速度位置关系

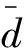
综上建立如下关系式：

d′=U×ys×(α+βxs)

(5)

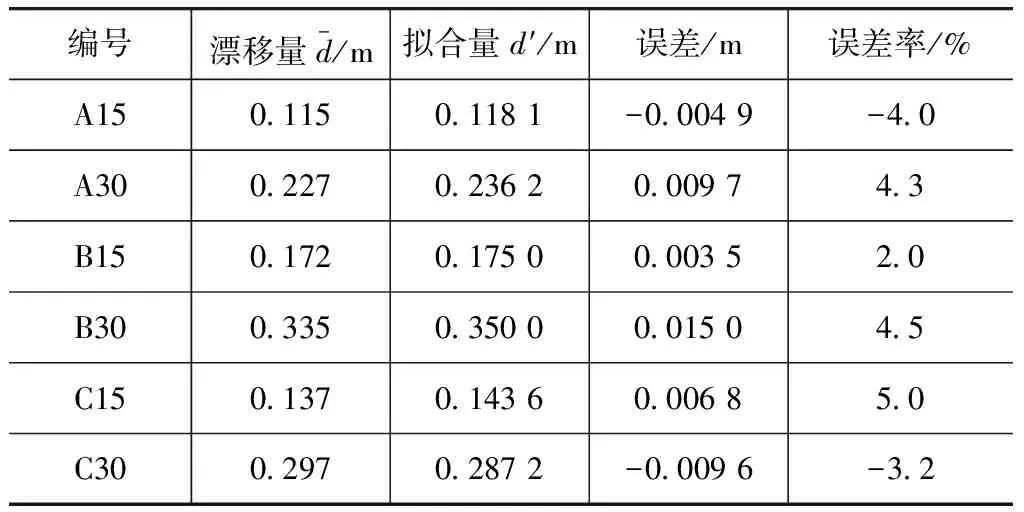
表2 拟合误差

根据情况保留3位有效数字，最终的声漂移量预测公式为

d′=U×ys×(0.00146+0.000391xs)

(6)

用第3.3节中数据对式(6)进行验证，结果如表3所示。

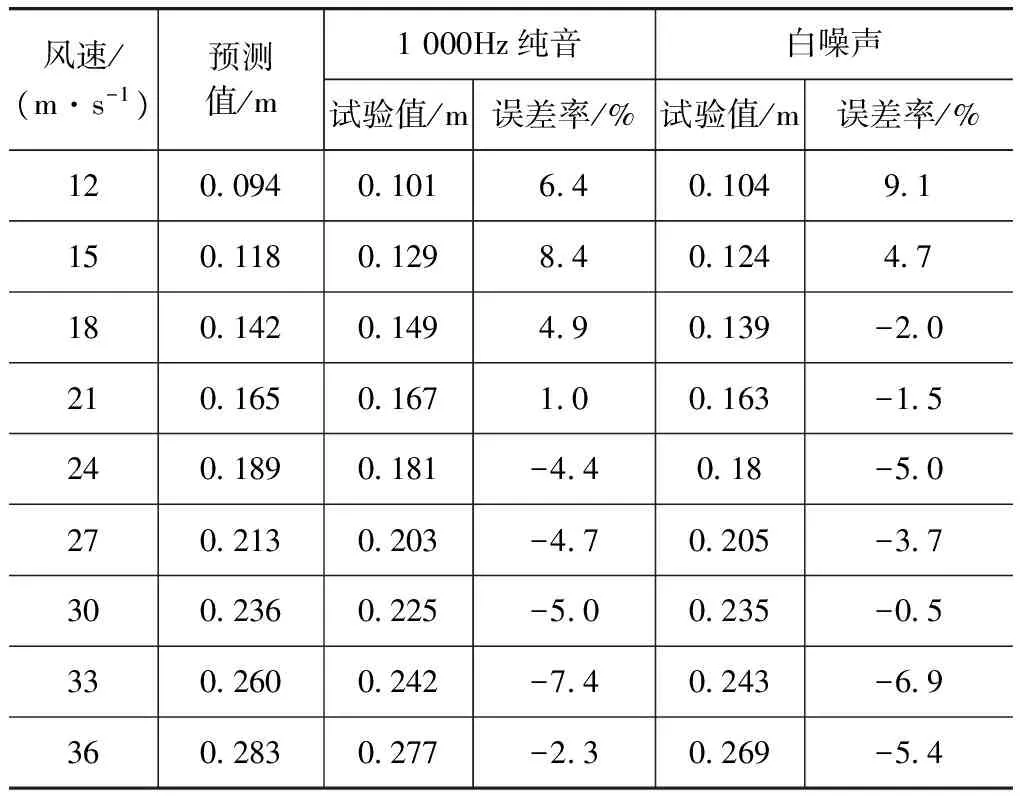
表3 预测公式对更多风速的拟合误差

对所有风速的声漂移量预测，其误差率均小于10%，考虑到声漂移量试验也有一定的误差，证明此预测公式有较好的准确性和适应性，可用于风洞试验中的声源漂移量预测与修正。

5 结论

本文中首先介绍了几何声学求解射流声传播路径的方法及其在整车风洞试验应用的不足之处。然后设计翼型声源，用传声器阵列进行声源定位，改变射流速度、声源信号、声源位置和测量点等多种参数，通过试验研究整车声学风洞中的声漂移现象。结果显示，在大尺寸3/4开口式喷口、低马赫数情况下：(1)声信号的频率与带宽、声源的高度位置和测量阵列的位置对声漂移量没有直接的影响；(2)声漂移量与射流的速度成正比；(3)声漂移量与声源在射流中径向距离基本成正比；(4)受剪切层厚度的影响，声漂移量随着轴向距离一起增大。最后，拟合出整车风洞中声漂移量的预测公式d′=U×ys×(0.00085+0.0005xs)，并验证了其精度和适用范围。

[1] BALSA T F. Refraction and shielding of sound from a source in a jet[J]. Journal of Fluid Mechanics,1976,76(76):443-456.

[2] AMIET R K. Refraction of sound by a shear layer[J]. Journal of Sound & Vibration,1976,1(4):467-482.

[3] AMIET R K. Correction of open jet wind tunnel measurements for shear layer refraction[C]. AIAA Conference on the Exploration of the Outer Planets,1975,75-532.

[4] MUELLER T J. (ED). Aero-acoustic measurement[M]. Germany: Springer,2002:34-41.

[5] SCHLINKER R H, AMIET R K. Refraction and scattering of sound by a shear layer[J]. Journal of the Acoustical Society of America,1981,70(6):1797-1799.

[6] SANFORD J. Acoustic refraction: a three dimensional shear layer correction for microphone measurements in an open-jet acoustic wind tunnel[J]. Journal of Undergraduate Research,2008,10(1):1-12.

[7] 贾青,杨志刚,李启良.汽车风洞试验段流场的试验研究[J].实验流体力学,2011,12(6):33-37.

An Experimental Study on the Effects of Jet Flow in Wind Tunnel forFull-scale Vehicle on Sound Propagation Path

Shen Zhe, Wang Yigang, Yang Zhigang & Li Fangxu

1.SchoolofAutomotiveStudies,TongjiUniversity,Shanghai201804;2.TongjiUniversity,ShanghaiAutomotiveWindTunnelCenter,Shanghai201804

An experimental study on the effects of the jet structure of the wind tunnel for full-scale vehicle on sound propagation path is conducted. Airfoil speaker is designed with a microphone array used to locate sound source, and the sound drift in full scale 3/4 open-jet wind tunnel under various parameter conditions are measured. Test results show that jet flow velocity and sound source location are more influential, while the effects of the type and height of sound source and measuring point location are ignorable. A prediction equation of sound drift in the wind tunnel for full-scale vehicle is fitted out based on test data, with its accuracy and application scope verified.

wind tunnel；jet flow；sound drift; microphone array

*国家自然科学基金(51375342)资助。

2016227

原稿收到日期为2015年10月30日，修改稿收到日期为2015年12月24日。