计及运动副间隙的独立悬架汽车摆振动力学建模与分析*

张 磊,卢剑伟,姜俊昭,燕培磊,李 磊

(1.合肥工业大学机械与汽车工程学院，合肥 230009； 2.江淮汽车股份有限公司技术中心，合肥 230601)

计及运动副间隙的独立悬架汽车摆振动力学建模与分析*

张 磊1,卢剑伟1,姜俊昭1,燕培磊1,李 磊2

(1.合肥工业大学机械与汽车工程学院，合肥 230009； 2.江淮汽车股份有限公司技术中心，合肥 230601)

以采用麦弗逊式独立悬架和齿轮齿条转向器的车辆为对象，计及转向系运动副间隙的影响，应用拉格朗日方程建立了8自由度车辆摆振系统动力学模型。接着基于非线性动力学分析方法，通过数值仿真，分析了车速、间隙和簧下质量对前轮摆振幅度的影响。结果表明，在某些特定车速范围，前轮会发生较为严重的自激摆振，与试验结果基本吻合，验证了模型的正确性。

独立悬架汽车; 前轮自激摆振; 运动副间隙; 动力学建模

前言

前轮摆振是汽车普遍存在的一个现象，表现为转向轮绕主销的持续振动和转向盘的抖动等。摆振不仅和汽车操纵稳定性密切相关，而且由摆振引起的转向盘的持续振动会降低驾驶体验甚至导致驾驶疲劳，影响行车安全。前轮摆振总体上可分为强迫振动和自激振动两种。由于自激型摆振与轮胎的迟滞阻尼特性、轮胎定位参数、转向系、前悬架的结构参数和系统内部非线性因素等密切相关，而强迫振动只是在其基础上施加外部激励，故从汽车正向设计的角度来看，研究自激型摆振显得更有意义[1-4]。

20世纪90年代以前，学者们主要关注非独立悬架车辆的摆振问题，建立了考虑悬架因素的3自由度摆振模型，用于分析车辆摆振的机理[5]。90年代以后，独立悬架汽车保有量快速增加，尤其以麦弗逊式前独立悬架和齿轮齿条式转向机构的乘用车为甚，部分学者开始考虑独立悬架汽车的摆振问题[6]，但是相关研究对于独立悬架中复杂定位参数等因素的考虑还不够全面。

先前的研究发现，非独立悬架车辆转向系的运动副对车辆摆振动力学响应有显著影响[7]。此外，某车型的市场反馈显示：该车型使用一段时间后，在中低车速段，车辆转向系自激摆振现象加剧。本文中针对此现象，以该车型参数为基础，采用麦弗逊式独立悬架和齿轮齿条式转向器，建立了计及转向系运动副间隙的8自由度摆振动力学模型，并进行针对相关参数的分析。通过算例，考察了车速、间隙和簧下质量对前轮摆振响应的影响，相关结果与实际情况基本吻合，可为独立悬架在役车辆摆振动力学分析提供借鉴。

1 动力学模型的简化

因前轮摆振涉及的车辆系统较为复杂，故结合麦弗逊独立悬架车辆特征进行必要的简化，以确保结论可信的前提下降低建模难度。整个模型分为3个子系统：悬架与定位参数、转向机构和轮胎。简化后的系统包含8个自由度：左、右前轮转角θL和θR，左、右前悬架下摆臂转角ψL和ψR，左、右转向拉杆转动自由度φ4和φ3以及左、右转向拉杆与转向齿条共有的平动自由度xr和转向齿轮转动自由度θp。据此列出总系统的动能、势能和耗散能，利用拉格朗日方程得出动力学模型。

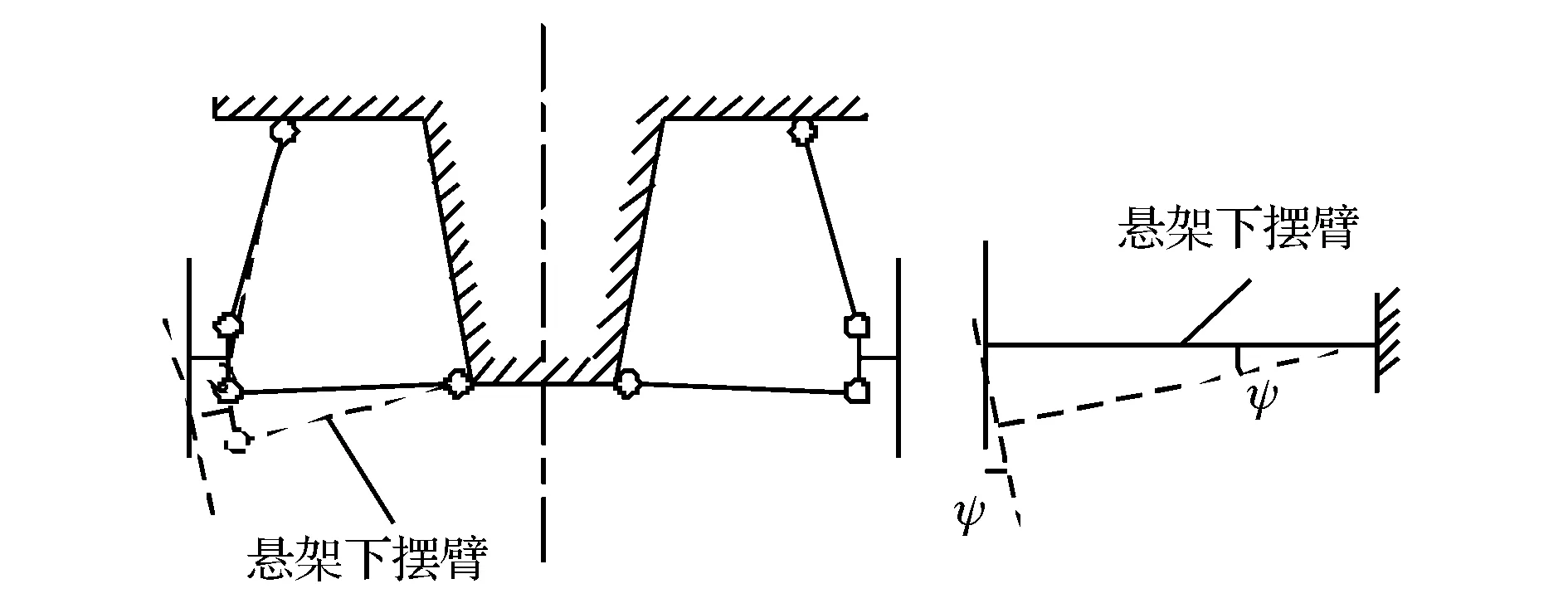
图1 麦弗逊式悬架简化示意图

假设汽车在平坦路面上以匀速v直线行驶，忽略风阻，不考虑簧上的车身自由度和路面与动力总成振动对轮胎的激励。独立悬架断开式车轴的设计，有别于非独立悬架，它降低了与转向系动力学耦合的影响，因此在悬架上仅考虑下摆臂绕其与副车架联结处轴线的旋转自由度，将悬架简化为仅在下摆臂外端运动方向上的弹簧阻尼机构，如图1所示。横向稳定杆只考虑其扭转刚度，并等效成一根无质量的扭转弹簧；前轮定位参数中,只考虑对摆振影响较大的主销后倾角和内倾角。充分考虑麦弗逊式独立悬架变化的虚拟主销轴线对前轮定位参数的影响，如图2所示。

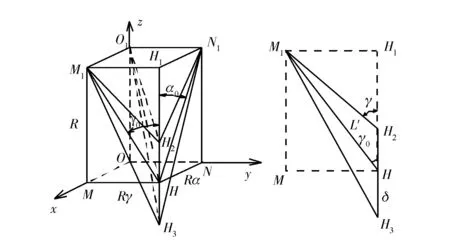
图2 主销轴线变化示意图

图2中，O1点为筒式减振器上铰链中心，H点为下摆臂外端的球铰链中心，O1H所在轴线即为虚拟的主销轴线，L为其长度，L′为其在x轴方向上投影的长度，γ0为初始主销后倾角，α0为初始主销内倾角，O1H2和O1H3可视为下摆臂发生微小角度位移ψ时主销轴线的变化，δ为下摆臂外端球铰链中心在垂直方向上的位移，可认为δ=Bψ,其中B为下摆臂与副车架联接处轴线与车轮纵向中心平面的距离。由此可得随下摆臂参数而变化的主销内倾角和后倾角为

(1)

(2)

假定转向盘固定不动，从转向齿轮到转向盘简化成为弹簧阻尼机构。将转向梯形机构看成平面五杆机构,且视为垂向受约束的刚体。考虑左、右转向节臂分别与左、右转向拉杆之间球铰的间隙和齿轮齿条的啮合侧隙，均采用“二状态”模型来描述含间隙运动副的动力学特性[8]。考虑到摆振的幅度很小，导致使齿轮齿条机构运动的幅度也很小，故为简化模型，不考虑齿形误差带来的内部激励，且用平均啮合刚度代替时变啮合刚度，简化后的转向系如图3所示。当汽车直线行驶，不发生摆振现象时，θL=θR=0，由图3转向梯形的几何关系可得φ1=Φ+θR，φ2=π-Φ+θL，其中Φ=1.5rad，为转向梯形的初始底角，即左、右转向节臂在不发生转向时和x方向所夹之锐角，由该型车辆参数决定。φ1～φ4为描述4根杆件角位移的广义坐标，均定义为与x方向逆时针所夹的角度。

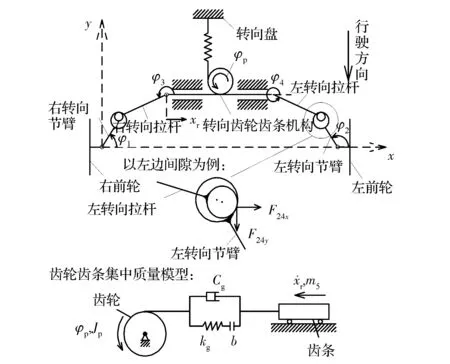
图3 转向系简化示意图

轮胎只考虑纯侧偏工况，无侧向滑移，且各轮胎侧偏特性相同。选用魔术公式模型模拟轮胎动态侧偏力变化：

FL=Sy+D0sin{C0arctan[B0(αL-Sx)·

(1-E0)+E0arctanB0(αL-Sx)]}

(3)

FR=Sy+D0sin{C0arctan[B0(αR-Sx)·

(1-E0)+E0arctanB0(αR-Sx)}

(4)

式中：FL和FR分别为左、右车轮所受侧偏力；αL和αR分别为左、右车轮的侧偏角；Sx，Sy，B0，C0，D0和E0均为魔术公式参数。利用文献[9]中所给参数值：Sx=0，Sy=0，B0=9.032rad-1，C0=1.29，D0=-5.25kN，E0=-0.801，可得到轮胎纯侧偏工况下侧偏力与侧偏角的关系。

根据文献[10]可建立轮胎滚动时车轮摆角和侧偏角之间的关系为

(5)

式中：σ为轮胎的松弛长度；a为轮胎的接地印记长度。

2 系统动力学方程的建立

系统的动能为

(6)

式中：IS为前轮总成换算到主销的转动惯量；Ia为下摆臂绕其与副车架联接点轴线的转动惯量；Ib为半轴绕其近端万向节转动惯量；m4和m3分别为左、右转向拉杆的质量；J4s和J3s分别为左、右转向拉杆的绕其质心转动惯量；m5为齿条所在杆件的质量；Jp为齿轮及其与转向盘之间转向柱绕其旋转轴的等效转动惯量；D为下摆臂在汽车横向轴线上的投影长度；A为汽车半轴前后万向节之间的长度。

系统的势能为

(7)

式中:kz为轮胎的垂向刚度；Lp和Lq分别为主销轴线与地面的交点至车轮与地面接触点的纵向距离和横向距离；α和γ分别为时变的主销内倾角和后倾角；kx为悬架弹簧在下摆臂运动方向上的刚度；kw为小齿轮到转向盘的等效刚度；ky为轮胎的侧向刚度；kb为横向稳定杆换算至下摆臂位移上的等效扭转刚度；R为车轮的滚动半径。

系统的耗散能为

(8)

式中：CS为车轮总成换算到主销的当量阻尼系数；Cx为悬架减振器在下摆臂位移上的阻尼系数。

对应于上述系统的8个自由度，可依次得出8个广义力分别为

F24x[l2sin(Φ-θL)+e24y+R4sinβ24]-

F24y[l2cos(Φ-θL)-e24x-R4cosβ24]

(9)

式中:Iy为车轮绕自身旋转轴的转动惯量；e为轮胎拖距；F24x和F24y分别为左间隙(左转事拉杆与左转向节臂之间球铰副的间隙)处的碰撞力在x和y方向上分量；l2为左转向节臂的长度；e24x和e24y分别为左间隙处偏心距在x和y方向上分量；β24为左间隙处的接触角；R4为左球头销的半径。

F13x[l1sin(Φ+θR)+R3sinβ13]-

F13y[l1cos(Φ+θR)+R3cosβ13]

(10)

式中:F13x和F13y分别为右间隙(右转向拉杆与右转向节臂之间球铰副的间隙)处的碰撞力在x和y方向上分量；l1为右转向节臂的长度；β13为右间隙处的接触角；R3为右球头销的半径。

(11)

(12)

Q5=-F24x(-l4sinφ4-R4sinβ24)-

F24y(l4cosφ4+R4cosβ24)

(13)

式中l4为左转向拉杆的长度。

Q6=F13x(-l3sinφ3-e13y-R3sinβ13)-

F13y(-l3cosφ3-e13x-R3cosβ13)

(14)

式中：l3为右转向拉杆的长度；e13x和e13y分别为右间隙处偏心距在x和y方向上分量。

(15)

(16)

式中：kg和Cg分别为齿轮齿条的平均啮合刚度和啮合阻尼；rp为转向齿轮分度圆半径；f(x)为描述含有齿轮侧隙的齿轮啮合力的非线性函数。设齿轮齿条的啮合侧隙为2b，则函数f(x)为

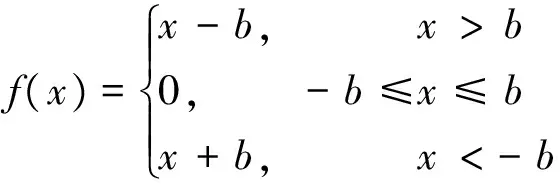
(17)

基于上述分析，应用第二类拉格朗日方程则可得出系统的动力学微分方程为

F24x[l2sin(Φ-θL)+e24y+R4sinβ24]+

F24y[l2cos(Φ-θL)-e24x-R4cosβ24]=

0

(18)

F13x[-l1sin(Φ+θR)+R3sinβ13]+

F13y[l1cos(Φ+θR)+R3cosβ13]=0

(19)

(kzB2+kxB2+kyR2+kb)ψL-kbψR+

kzB(Lpγ-Lqα)θL+FLR=0

(20)

(kzB2+kxB2+kyR2+kb)ψR-kbψL+

kzB(Lpγ-Lqα)θR-FRR=0

(21)

F24x(-l4sinφ4-R4sinβ24)+

F24y(l4cosφ4+R4cosβ24)=0

(22)

F13x(-l3sinφ3-e13y-R3sinβ13)+

F13y(-l3cosφ3-e13x-R3cosβ13)=0

(23)

(24)

kwθp=0

(25)

3 算例分析与讨论

该车型以往的试车结果发现，车辆在中、低速时会发生较为明显的摆振现象，可以此为依据定性验证所建动力学模型的正确性，从而运用该动力学模型对车辆摆振响应进行分析。该车型主要参数见表1，运用2阶改进的Rosenbrock算法进行数值求解。

图4为左轮摆角的最大值随车速的变化曲线，车速范围为10-130km/h，假设车轮受到路面不平的冲击，造成左前轮的转角θL的初值为0.001rad,运动副间隙可根据实际工程经验取值，其中球铰链间隙为0.5mm,齿轮齿条啮合侧隙取值为0.2mm。可以看出，在整个较大的中低速范围内，车辆都会发生摆振现象，尤其在40-70km/h的范围内程度相对剧烈，和实际情况基本吻合。

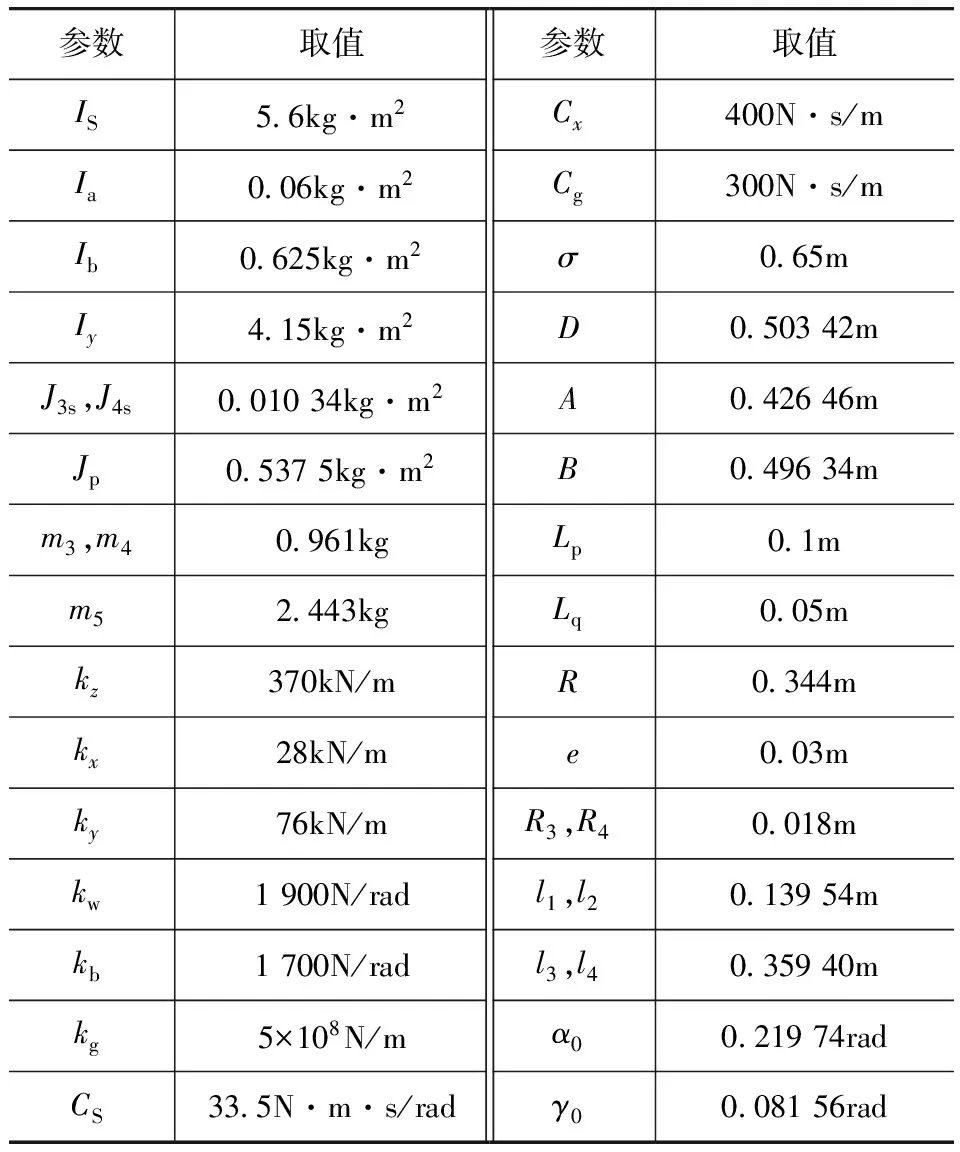
表1 某独立悬架汽车摆振模型参数

图4 左轮摆角最大值随车速变化曲线

其中，车速为50km/h时的动力学响应如图5所示。车轮在受到初始激励后，会在较短的时间内达到稳定状态持续振动，为一典型的自激振动现象。此时运动形态为拟周期运动向混沌运动的过渡阶段，形态较为复杂，不利于工程控制。

图5 车速为50km/h时左轮摆角动力学响应

图6为球铰间隙r、齿轮侧隙b均为0.5mm和球铰间隙r、齿轮侧隙b均为0.2mm两种情况下左轮摆角最大值随车速的变化曲线对比，可以看出间隙大小在摆振车速范围内的影响较为敏感。随着车辆使用时间的增加，转向系运动副不可避免地会因磨损出现间隙，而间隙对摆角的幅值有着较大的影响，故在车辆摆振动力学建模分析中计及运动副间隙有重要意义。

图6 两种间隙下左轮摆角最大值随车速变化曲线对比

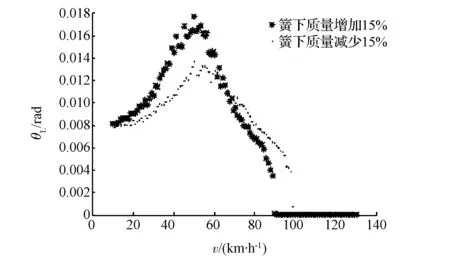
图7 两种簧下质量下左轮摆角最大值随车速变化曲线对比

在轮胎总成不变的情况下，悬架结构很大程度上决定了簧下质量的大小。因此对于探求悬架因素与转向机构因素耦合下的摆振动力学模型，有必要考察簧下质量因素的影响。图7为簧下质量的变化对摆振幅度的影响。其中球铰间隙为0.5mm，齿轮侧隙为0.2mm，实心点线为簧下各部件质量相对原值均匀地减少15%；星点线为均匀地增加15%。可以看出：簧下质量的大小对摆振的区间和幅值大小均有一定的影响，簧下质量减小会使整个曲线右移，体现在发生摆振最大值的车速升高，且发生摆振的车速范围会向高车速方向扩大；而增加簧下质量的结果则相反，虽会缩短摆振发生的车速区间长度，但在发生摆振现象较为剧烈的车速段，即40-70km/h，其摆角幅值要明显大于减小簧下质量的情况。

4 结论

本文中利用拉格朗日方程建立了考虑转向系运动副间隙的麦弗逊式独立悬架汽车8自由度动力学模型，并应用数值算例分析了车速、间隙和簧下质量对摆振幅度的影响，得出如下结论。

(1)通过所建模型计算车轮摆角最大值随车速的变化曲线，确定了自激摆振发生的速度区间和发展趋势，相关结论与该车型实际试车情况基本吻合，从而验证了模型的准确性。

(2)计及转向系运动副间隙时，某一固定车速下的车轮摆振运动形态较为复杂，为拟周期运动向混沌运动的过渡阶段，不易于工程控制。

(3)通过计算两种间隙下和两种簧下质量下的车轮摆角随车速的变化曲线表明：间隙因素和悬架因素对摆振的影响不容忽视，将这两种因素纳入摆振动力学建模中对工程实际的指导有着重要意义。

[1] PACEJKA H B. Analysis of the shimmy phenomenon[J].Proceedings of the Institution of Mechanical Engineers Automobile Division, 1965, 180(1965):251-268.

[2] LINDSLEY N J. A new tire model for aircraft landing gear dynamics[D].Ohio:University of Akron, 1999.

[3] 宋健.导向轮轮胎和定位参数对汽车摆振的影响及整车横向动力学优化分析[D].北京：清华大学，1987.

[4] DEMIC M. Analysis of influence of design parameters on steered wheels shimmy of heavy vehicle[J]. Vehicle System Dynamic, 1996，26(5)：343-362.

[5] 管迪华,何泽民,肖田元.汽车转向轮摆振的仿真计算研究[J].汽车工程, 1982,4(1):33-38.

[6] 贺丽娟,焦志勇.麦弗逊悬架优化设计及其对摆振的影响[J]. 天津科技大学学报, 2009, 24(5):50-53.

[7] LU Jianwei, GU Jue, LIU Mengjun. Modeling of the vehicle shimmy system with consideration of clearance of the steering mechanism[J]. Meccanica, 2010, 45(1):53-61.

[8] 杨义勇,金德闻.机械系统动力学[M].北京:清华大学出版社,2009.

[9] 林逸,李胜.非独立悬架汽车转向轮自激型摆振的分岔特性分析[J].机械工程学报,2004,40(12):187-191.

[10] GERHARD S. Shimmy analysis of a simple aircraft nose landing gear model using different mathematical method[J]. Aerospace Science and Technology, 1997, 1(8): 545-555.

Dynamics Modeling and Analysis on Shimmy in Independent Suspension Vehicle with Consideration of Clearances in Kinematic Pairs

Zhang Lei1, Lu Jianwei1, Jiang Junzhao1, Yan Peilei1& Li Lei2

1．SchoolofMechanicalandAutomotiveEngineering,HefeiUniversityofTechnology,Hefei230009;2.PassengerCarofResearchCenter,AuhuiJianghuaiAutomobileCo.,Ltd.,Hefei230601

Taking a vehicle with McPherson independent suspension and rack/pinion steering mechanism as objective, with consideration of the effects of clearances in the kinematic pairs of steering system, an eight DOF dynamics model for vehicle shimmy is established by applying Lagrange equation. Then based on nonlinear dynamics analysis, a numerical simulation is conducted on the model to analyze the effects of vehicle speed, clearances and unsprung mass on the shimmy amplitude of front wheels. The results show that rather serious self-excited shimmy may happen on front wheels at some specific speed ranges, which basically well agree with test results, verifying the correctness of the model built.

independent suspension vehicle; front wheel self-excited shimmy; clearances in kinematic pairs; dynamics modeling

*国家自然科学基金(50975071)、教育部新世纪优秀人才支持计划(NCET-10-0358)和安徽省高等学校省级自然科学研究重大项目(KJ2014ZD06)资助。

2016233

原稿收到日期为2015年9月25日，修改稿收到日期为2015年12月24日。