并网逆变器死区效应消去补偿方法研究

贾学瑞，粟时平，刘桂英，吕 超，张 意



并网逆变器死区效应消去补偿方法研究

贾学瑞，粟时平，刘桂英，吕 超，张 意

(智能电网运行与控制湖南省重点实验室(长沙理工大学)，湖南 长沙 410004)

针对并网逆变器死区效应问题，在充分分析并网逆变器工作特点及零电流箝位现象的基础上，提出了一种新颖的逆变器死区效应消去补偿方法。该方法在非过零区域依据并网电流的方向选择有效开关管，屏蔽无效开关，在过零区域根据并网电流的大小进行前馈补偿。与传统死区消去和补偿方法相比，该方法充分考虑了零电流箝位现象，能够更好地抑制电流过零处逆变器输出电压波形畸变，有效消除了死区效应的影响，降低输出电压谐波含量，从而改善并网电流质量。利用Matlab/Simulink仿真软件进行了仿真验证，仿真结果证明了逆变器死区效应消去补偿方法的有效性和正确性。

并网逆变器；死区效应；零电流箝位；消去；补偿

0 引言

分布式并网发电是可再生能源利用的主要方式之一[1]。并网逆变器是分布式电源与电网的接口装置[2]，它将分布式电源产生的电能转换为电网可以接受的电能。因此，逆变器并网已成为当前的研究热点[3]。但是并网发电会产生谐波污染，降低电能质量。理想状况下，并网逆变器输出电流包含开关频次及其整数倍的谐波，这部分高次谐波可以通过滤波器滤除[4]。然而，在实际应用中，开关器件存在开通延迟和关断延迟，为了防止同一桥臂的“直通”现象，通常将开通信号延迟一个死区时间后发出，这将导致输出电压畸变，基波电压减小，造成并网电流谐波含量增大。由于分布式电源容量所占比例不断扩大，逆变器谐波电流会对多逆变器系统与电网在公共连接点处形成的分布式阻抗网络激励而使其发生交互作用，这对系统的稳定运行构成了潜在威胁[5]。近年来，逆变器死区效应问题得到了广泛的研究并提出了不同方法。这些方法主要包括：脉冲宽度调整法[6-7]、死区时间补偿方法[7-10]、死区时间消去方法[11-13]。脉冲宽度调整法，实现起来较为复杂，会占用控制器大量计算资源。对于死区时间补偿方法，由于死区效应和开关器件都具有非线性的特点，这类补偿方法很难完全消除死区效应。死区消去方法，其主要特征是将一相桥臂分解为两个部分，每一部分包括一个可控开关管及一个二极管，根据电流极性选择工作部分。因此，死区消去策略的主要问题是准确获得电流极性及开关状态。然而，由于纹波电流和采样精度、采样延时的影响，逆变器在过零区域电流极性很难准确检测。其中文献[11]提出了一种采用检测二极管导通状态判断电流极性，进行死区时间插入的方法，但是该方法需要增加额外硬件电路投资。文献[12]提出了一种通过电流空间矢量所在的区域判断相电流极性，插入无效死区时间的方法，但并未考虑零电流箝位现象。文献[13]提出了一种并网逆变器死区效应消去补偿方法，该方法未能充分考虑零电流箝位现象，在过零区域的每个载波周期均补偿一个死区时间的误差电压，补偿不够准确。在电机控制中，文献[14]提出了一种设置夹断区间，在过零区域和非过零区域分别进行补偿的方法，但是该方法将过零区域完全采用线性补偿，补偿不够准确。

针对逆变器设定死区时间产生的死区效应问题，本文在详细分析逆变器死区效应及零电流箝位现象的基础上，提出了一种逆变器死区效应消去补偿方法。该方法采用并网电流定向，为降低开关损耗，在非过零区域屏蔽无效开关，无需插入死区时间；将过零区域分为线性补偿区域及无误差区域，仅在线性区域进行补偿，从而更好地减小死区效应的影响。所提方法无需增加硬件设备，实现简单方便，较好地消去死区效应影响并在Matlab/Simulink软件中进行了仿真验证，仿结果证明所提方法是有效的。

1  并网逆变器死区效应分析

理想情况下，逆变器同一桥臂的上下开关管总是互补开通关断，由于开关器件的非理想特性，器件的开通和关断都需要一定的时间，且一般关断时间大于开通时间。为了防止同一桥臂两个开关管直通现象，通常在上下开关控制信号之间插入死区时间如图1。阴影部分为逆变器死区时间。

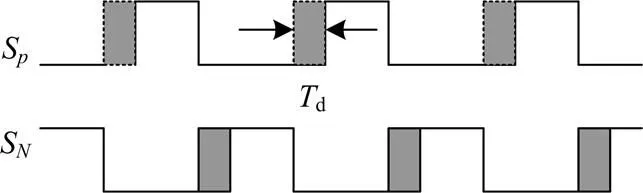
图1 插入死区时间的控制序列

为了表述方便，以单相并网逆变器为例说明死区效应的影响。

单相并网逆变器的主电路如图2所示，主要包括滤波电感12，滤波电容，开关器件T1—T4，反并联二极管VD1—VD4。V为直流侧电压，1为机侧电流，2为网侧电流，u为电网电压。

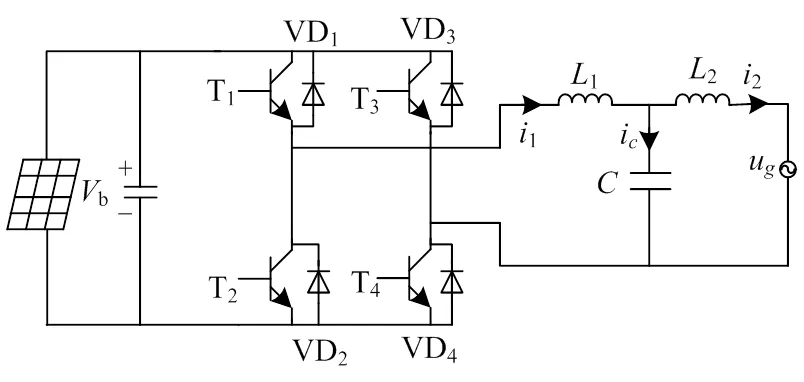
图2 单相光伏并网逆变器主电路图

设定电流1流向电网侧为正，流向逆变器侧为负。图3(a)所示1>0时，在死区时间内电流通过二极管VD2、VD3续流，输出电压被箝位在-V；图3(b)所示1<0时在死区时间内，电流通过VD1、VD4续流，输出电压被箝位在V。图3中14、23表示T1、T4和T2、T3的理想控制信号，表示逆变器理想输出电压；14R、23R表示T1、T4和T2、T3的实际控制信号，R表示逆变器实际输出电压，Δ表示逆变器一个载波周期T输出误差电压。

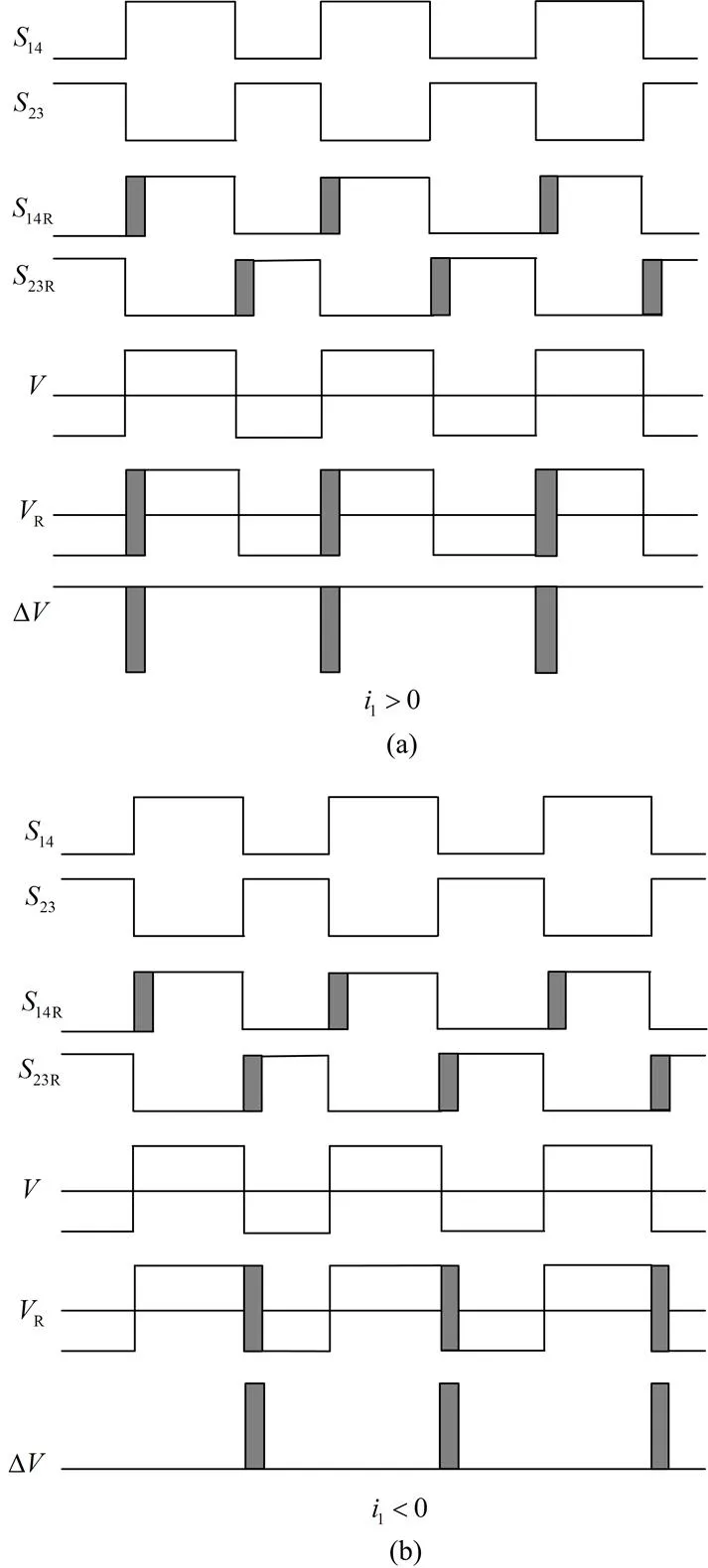
图3 死区时间对逆变器输出电压的影响

以上分析表明输出误差电压Δ取决于电流1的方向，误差电压为

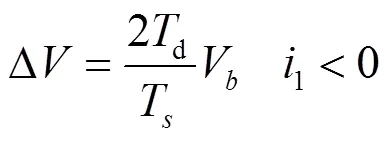
(2)

从以上分析可以看出,误差电压呈周期方波特性，将导致逆变器输出电压畸变，基波幅值跌落，从而影响并网电流质量。

2  并网逆变器零电流箝位现象分析

逆变器工作过程中，理想情况下，在电流过零点附近，电感电流随开关占空比的减小而逐渐减小到0，电流在过零点附近不会出现零电流箝位现象。由于死区时间的插入，在过零点附近，当dTdT>d才会退出零电流区域，这种现象就是零电流箝位现象。由于零电流箝位现象的存在，致使在过零区域逆变器输出误差电压不再是幅值为2V，持续时间为d的方波电压。因此，为了更好地消去死区效应的影响，需要考虑零电流箝位现象，以下为零电流箝位现象的详细分析。

在死区时间内，所有开关管均关断，电感电流通过二极管续流。为讨论零电流箝位现象，首先应分析二极管续流模式，所有的二极管续流包含三种模式[15]，如图4所示。

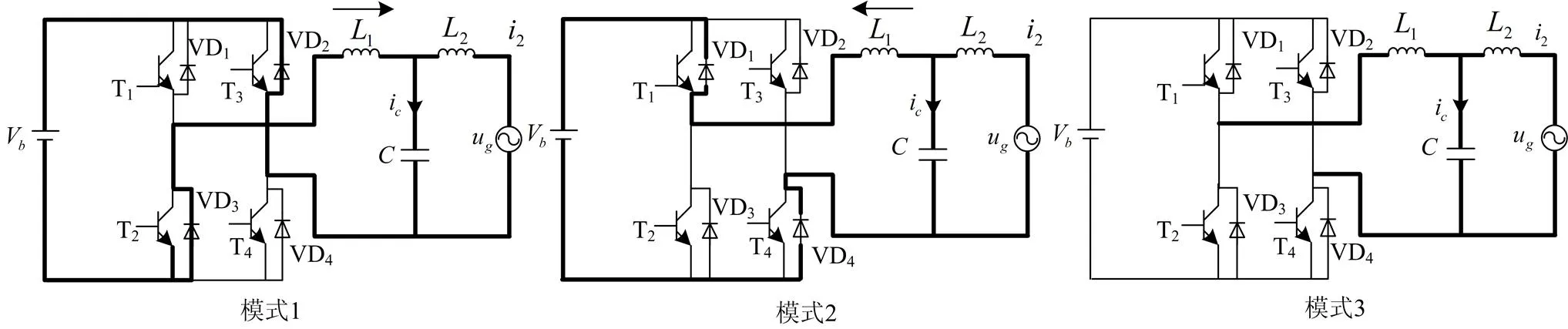
图4 死区时间内二极管工作模式

模式1，电感电流为正，二极管VD2VD3导通续流，此时逆变器桥臂输出电压为-V。

模式2，电感电流为负，二极管VD1VD4导通续流，此时逆变器桥臂输出电压为V。

模式3，电感电流为零。此时逆变器桥臂输出电压为0。

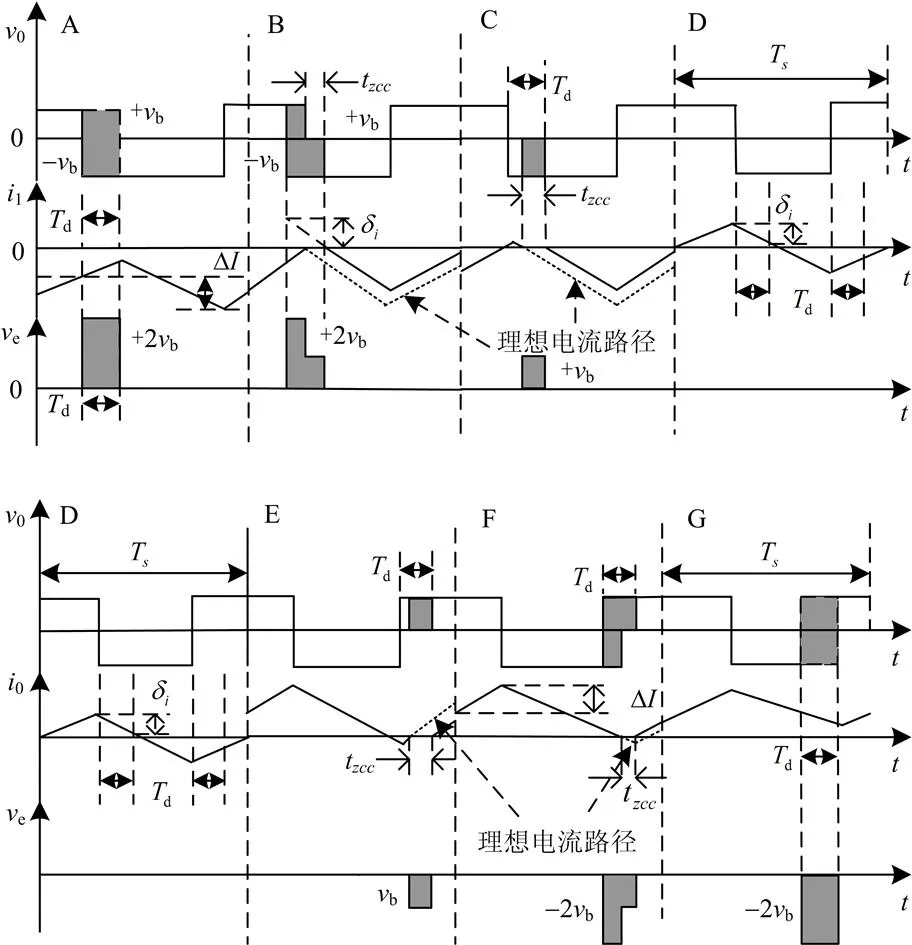
图5 零电流箝位现象分析

图5以电感电流由负向正变化为例，对零电流箝位现象进行了详细的分析。从图中可以看出，开关管有7种工作模式，零电流箝位现象出现在B、C，E、F模式中。

图中A，实际电感电流为负，不存在零电流箝位现象，逆变器桥臂输出误差电压e的幅值为2 V，持续时间为d。

图中B，实际电感电流为负，存在零电流箝位现象，逆变器桥臂输出误差电压e由两部分组成，其中一部分是幅值为2V，持续时间为d-t的误差量；另一部分是幅值为V，持续时间为t的误差量。

图中C，实际电流为负，存在零电流箝位现象，逆变器桥臂输出误差电压e的幅值为V，持续时间为t。

图中D，实际电感电流过零区域，不存在零电流箝位现象，逆变器桥臂输出误差电压为零。

图中E，实际电感电流为正，存在零电流箝位现象，逆变器输出误差电压e的幅值为-V，持续时间为t。

图中F，实际输出电压为正，存在零电流箝位现象，逆变器输出误差电压e由两部分组成，其中一部分是幅值为-2 V，持续时间为d-t的误差量；另一部分是幅值为-V，持续时间为t的误差量。

图中G，实际输出电压为正，不存在零电流箝位现象，逆变器输出误差电压e的幅值为-2V，持续时间为d。

如上分析，所有可能的电压误差如表1所示。

表1 死区电压误差

3  逆变器死区消去补偿方法

如图6所示逆变器一相桥臂示意图，当1＞0时，在TP开通阶段，电感电流流过TP；在TP关断阶段，电感电流通过DN续流。而在整个开关周期开关管TN和DP均无电流流过。因此，开关管TN和二极管DP可以屏蔽，此时单桥臂可以等效为P型开关单元(如图6)，在单相并网逆变器中，相当于T2、T3(控制信号相同)为无效开关管。同理，当1＜0时，在TN开通阶段，电感电流流过TN；在TN关断阶段，电感电流通过DP续流。而在整个开关周期开关管TN和DP均无电流流过。因此，开关管TN和二极管DP可以屏蔽，此时单桥臂可以等效为N型开关单元(如图6)，在单相并网逆变器中，相当于T1、T4(控制信号相同)为无效开关管。实际上单相桥臂根据电流方向的不同，可以拆分成P型开关单元和N型开关单元，由于每个桥臂均由一个开关管和一个二极管组成，因此只要屏蔽相应的无效开关管，则死区效应可以被完全消除。

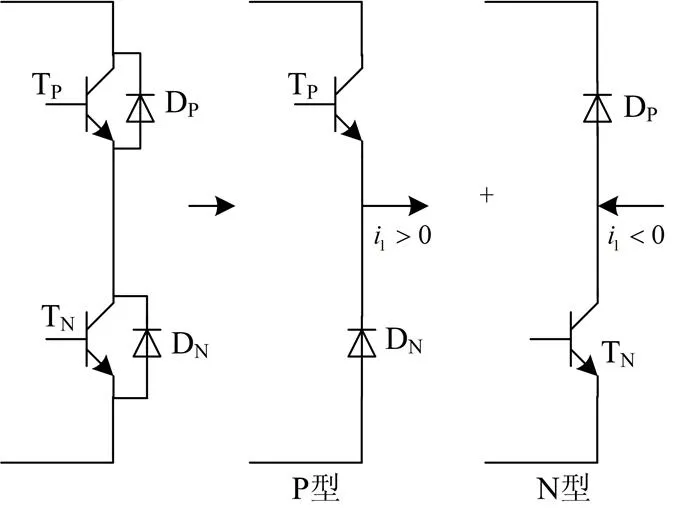
图6 等效桥臂分解单元结构

然而由于电感纹波电流的影响以及采样精度和采样延时等原因，在过零区域电感电流方向难以准确测量，因此上述方法不再适用。结合图5在A、G模式下，采用屏蔽无效开关的方法，可以较好地消去死区效应的影响；B、C和E、F模式下，则采用前馈补偿方式消去死区效应的影响；D模式插入死区时间不影响逆变器输出电压，不需要进行补偿。

由以上分析可知，确定逆变器不同的运行模式并采用相应的消去补偿方法可以较好地消除死区效应，得到以下消去补偿策略。

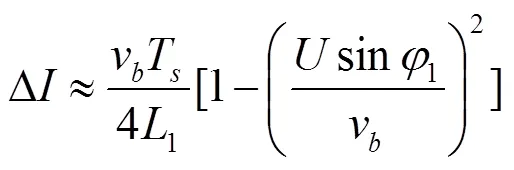
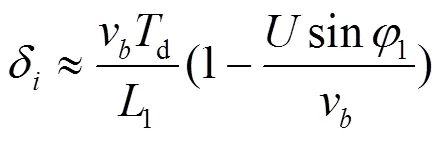
(5)

在E、F模式下，电感电流的取值范围为Δ-δ<1<Δ，补偿的电压为

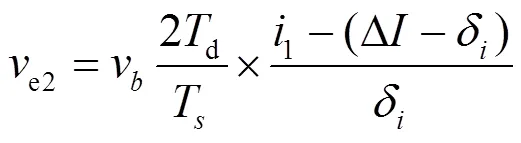
因此，整个控制策略流程图如图7所示。图中ref为占空比参数，com为补偿量。com计算如下所示。

(7)

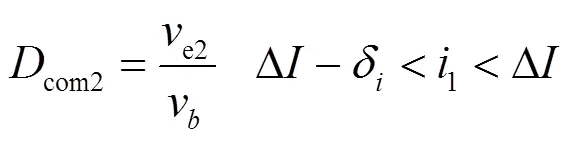
4  仿真验证

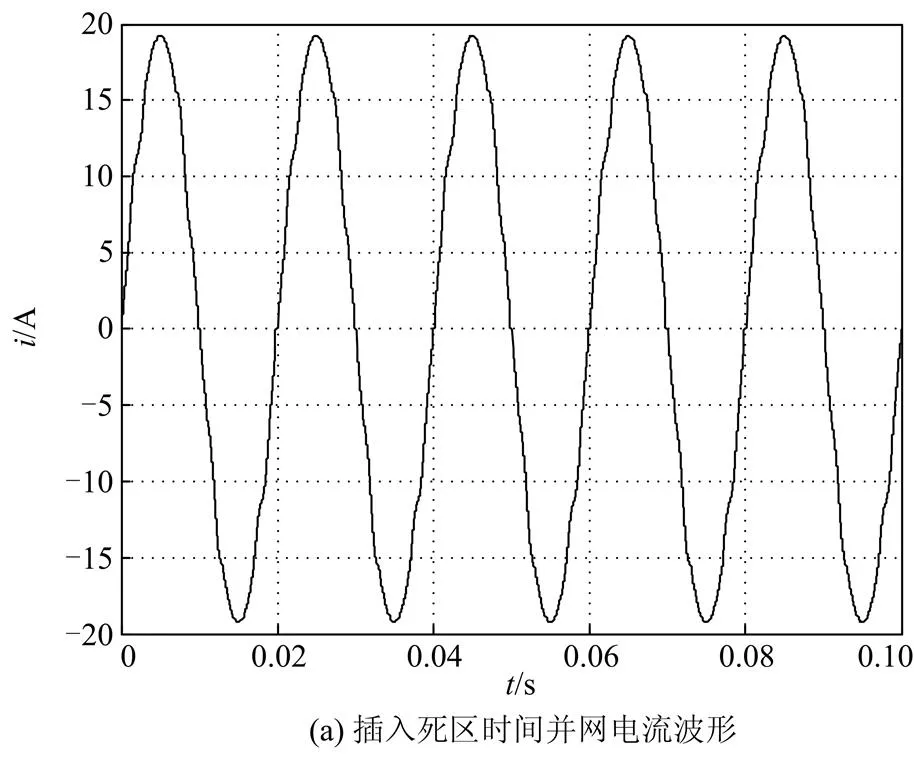
为了验证本文所提的控制方法，以图1所示主电路建立仿真模型，其中滤波电感1=0.6 mH，2=0.15 mH，滤波电容=10 μF，直流电压360 V，电网电压220 V，开关频率10 kHz，采用双极性调制，死区时间设为2 μs。仿真波形如图8所示。

图8(a)分别为逆变器插入2 μs死区时间，从图中可以看出，插入死区时间后，并网电流波形发生明显的畸变，并网电流畸变率=3.39%。

图8(b)采用文献[14]所提方法并网电流的波形图，此时并网电流总谐波畸变率反而升高(= 4.26%)。这是由于过零区域中无误差区域的误补偿电压，导致含LCL滤波器的阻抗网络发生谐振，使得并网电流总谐波畸变率升高。

5  结论

本文通过详细分析并网逆变器桥臂工作特点及零电流箝位现象，提出了一种新颖的并网逆变器死区效应消去补偿方法。与传统方法相比，该方法能充分考虑零电流箝位现象，更好地消除逆变器死区效应的影响，降低并网电流总谐波畸变率，且方法简单不需要增加额外的硬件设备。

[1] BLAABJERG F, TEODORESCU R, LISERRE M. Overview of control and grid synchronization for distributed power generation and grid synchronization for distributed power generation system[J]. IEEE Transactions on Industrial Electronics, 2006, 53(5): 1398-1409.

[2] 雷亚雄, 李建文, 李永刚. 基于准PR调节器电流双闭环LCL三相并网逆变器控制[J]. 电力系统保护与控制, 2014, 42(12): 44-50.

LEI Yaxiong, LI Jianwen, LI Yonggang. Control strategy of three-phase LCL grid-connected inverter based on quasi-PR adjuster[J]. Power System Protection and Control, 2014, 42(12): 44-50.

[3] 黄东东, 吴在军, 窦晓波, 等. 光伏规模化并网的电能质量复合控制策略研究[J]. 电力系统保护与控制, 2015, 43(3): 107-112.

HUANG Dongdong, WU Zaijun, DOU Xiaobo, et al. A power quality composite control strategy based on large-scale grid-connected photovoltaic power generation[J]. Power System Protection and Control, 2015, 43(3): 107-112.

[4] 胡雪峰, 王璐, 龚春英, 等. 并网逆变器的补偿控制技术[J]. 高电压技术, 2010, 36(12): 3084-3089.

HU Xuefeng, WANG Lu, GONG Chunying, et al. Compensation technique of grid-connected inverter[J]. High Voltage Engineering, 2010, 36(12): 3084-3089.

[5] 许德志, 汪飞, 毛华龙, 等. 多并网逆变器与电网的谐波交互建模分析[J]. 中国电机工程学报, 2013, 33(12): 64-71.

XU Dezhi, WANG Fei, MAO Hualong, et al. Modeling and analysis of harmonic interaction between multiple grid-connected inverters and the utility grid[J]. Proceedings of the CSEE, 2013, 33(12): 64-71.

[6] 袁佳歆, 薛刚, 赵震, 等. 三相逆变器无死区最优矢量控制研究[J]. 电力系统保护与控制, 2014, 42(24): 18-24.

YUAN Jiaxin, XUE Gang, ZHAO Zhen, et al. New optimal dead-time elimination for three-phase voltage source inverters[J]. Power System Protection and Control, 2014, 42(24): 18-24.

[7] KYU M, WON S, YOUNG T, et al. A novel switching strategy for pulse width modulation power converters[J]. IEEE Transactions on Industrial Electronics, 2007, 54(1): 330-337.

[8] JONG-WOO C, SEUNG-KI S. Inverter output voltage synthesis using novel dead time compensation[J]. IEEE Transactions on Power Electronics, 1996, 11(2): 221-227.

[9]  NAOMITSU U, TOMONOBU S, TOSHIHIHISA F. Adaptive dead-time compensation strategy for permanent magnet synchronous motor drive[J]. IEEE Transactions on Energy Conversion, 2007, 22(2): 271-280.

[10]赵耀, 赵庚申, 郭天勇, 等. 基于SVPWM低谐波死区算法的研究应用[J]. 电力系统保护与控制, 2012, 40(8): 58-63.

ZHAO Yao, ZHAO Gengshen, GUO Tianyong, et al. Research and application of low harmonics dead-time injection based on SVPWM[J]. Power System Protection and Control, 2012, 40(8): 58-63.

[11] CHEN Lihua, FANG Zhengpeng. Dead-time elimination for voltage source inverters[J]. IEEE Transactions on Power Electronics, 2008, 23(2): 574-580.

[12]于兆凯, 颜钢锋, 林志赟, 等. 电压源逆变器死区效应的分析与消除[J]. 控制工程, 2012, 19(6): 1081-1084.

YU Zhaokai, YAN Gangfeng, LIN Zhiyun, et al. Dead-time effects analysis and elimination for voltage source inverter[J]. Control Engineering of China, 2012, 19(6): 1081-1084.

[13] WANG Yong, GAO Qiang, CAI Xu. Mixed PWM for dead-time elimination and compensation in a grid-tied inverter[J]. IEEE Transactions on Industrial Electronics, 2011, 58(10): 4797-4803.

[14]潘海鸥, 陈斌, 陈琳, 等. 考虑零电流箝位的永磁同步电机死区效应补偿方法[J]. 电机与控制应用, 2010, 37(10): 1-5.

PAN Haiou, CHEN Bin, CHEN Lin, et al. Dead-time compensation strategy for permanent magnet synchronous motor drive taking zero current clamp into account[J]. Electric Machines & Control Application, 2010, 37(10): 1-5.

[15] WANG Hongliang, PEI Xuehua, CHEN Yu, et al. An adaptive dead-time compensation method for sinusoidal PWM-controlled voltage source inverter with output LC filter[C] // Applied Power Electronics Conference and Exposition, Fort Worth, TX, 2011: 778-785.

[16] SCHELLEKENS J M, BIERBOOMS R A M, J DUART E. Dead time compensation for PWM amplifiers using simple feed-forward techniques[C] // International Conference on Electrical Machines, Rome, 2010: 1-6.

(编辑 周金梅)

A novel strategy of dead-time elimination and compensation for grid-tied inverters

JIA Xuerui, SU Shiping, LIU Guiying, LÜ Chao, ZHANG Yi

(Hunan Province Key Laboratory of Smart Grids Operation and Control (Changsha University of Science and Technology), Changsha 410004, China )

A novel dead-time elimination and compensation method based on full analysis of the feature of the grid-tied inverter and zero-current clamping phenomenon is presented to eliminate the dead-time effect of grid-tied inverter. The effective switch transistor is chosen according to the direction of grid current in the non-zero current zone and the control strategy is feed-forward compensation in the zero current zone. In comparison with traditional dead-time elimination and compensation methods, the proposed method can better restrain the output distortion in the zero current zone, effectively eliminate the dead-zone effect, reduce THD, and thereby improve grid-connected current quality due to full consideration of zero-current clamping phenomenon. The Matlab/Simulink simulation results demonstrate the effectiveness and validity of the proposed method.

grid-tied inverter; dead-time effect; zero-current clamping; elimination; compensation

10.7667/PSPC150870

2015-05-24；

2015-11-27

贾学瑞(1989-)，男，硕士研究生，研究方向为分布式电源并网技术；E-mail: 1606040986@qq.com 粟时平(1963-)，男，出站博士后，教授，主要研究方向为新能源发电，电力系统电能质量治理；E-mail: suship@ 126.com 刘桂英(1964-)，女，副教授，主要研究方向为分布式电源并网发电，电能质量监控及无功补偿。