基于遗传算法的有源电力滤波器滑模控制

张栋梁，谢业华，刘 娟，黄 开



基于遗传算法的有源电力滤波器滑模控制

张栋梁，谢业华，刘 娟，黄 开

(中国矿业大学信电学院，江苏 徐州 221008)

为改善滑模控制方式有源电力滤波器在高频处抖动的缺陷，提出用遗传算法对控制器参数进行优化，提高了控制器性能。简要说明了三相三线有源电力滤波器的工作原理，根据补偿电流和指令电流的误差构建滑模变结构控制器。详细给出了用遗传算法对控制器参数的优化过程，得到了控制器参数的确切值。通过对传统PI控制方式和优化后滑模控制方式进行仿真实验，结果表明，所提出的滑模控制方式响应速度快，算法简单，较好地抑制抖动，鲁棒性强，达到了优化的目的。

有源电力滤波器；滑模控制；遗传算法；参数优化；鲁棒性

0 引言

随着供电系统越来越复杂，各种电力电子装置被广泛应用，在低压配电网中电能质量问题日益突出，给电力设备正常运行带来了严重的影响。电能质量问题主要包括：电压闪变、三相不平衡和电流畸变等问题。营造一个“绿色”电网是十分必要的，一方面使电力系统安全、稳定运行，另一方面可以保障用电设备正常工作[1]。并联型有源电力滤波器(APF)利用PWM整流器拓扑结构，具有电流源特性，向电网注入补偿电流，以减小电源电流的畸变率，既能有效抑制谐波电流，还能起到无功补偿的目的，使网侧电流呈现正弦波[2]。谐波检测方法和电流控制策略，决定了APF抑制谐波电流效果的好坏。滞环控制方式、三角波控制方式、无差拍控制方式、空间矢量调制等，是目前常用的电流控制方法。滞环控制中，开关频率要随着电网电压峰值波动进行相应的波动。无差拍控制对系统模型的精确性要求高，在扰动下稳定性差。三角载波控制受到电力电子器件开关频率的限制，在高频段，控制性能低。空间矢量调制控制策略能保证电流的稳定性，但也存在控制算法复杂、运算时间长、系统实时性低等缺点[3]。

滑模控制能够跟踪系统状态，对系统参数变化和扰动不灵敏，稳定性好，响应快速。有源滤波器的主电路为电压型逆变器，通过控制开关器件的通断来控制电流的方向，其结构本身不断变化。基于上述特点，滑模控制在有源滤波器中能得到很好的应用[4]。

本文在并联有源电力滤波器时域分析的基础上，建立了滑模控制器模型。在建立好的模型基础上用改进的遗传算法对控制器进行参数优化。与经典双闭环矢量控制相比，仿真实验波形表明，改进后滑模控制器能获得更好的稳态性能和动态性能。

1 APF基本结构和数学模型

忽略线路阻抗，对理想并联型三相有源电力滤波器进行研究，建立时域下的数学模型。其结构原理如图1。

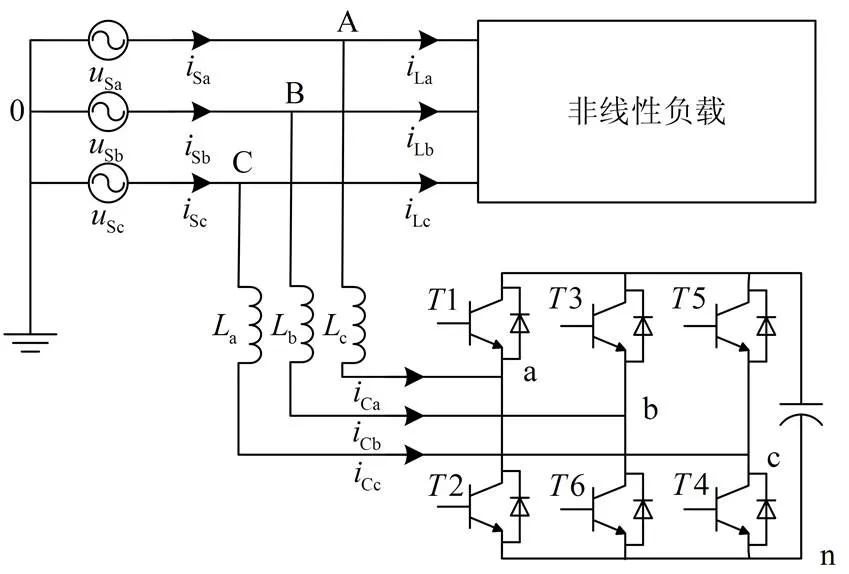
图1 APF系统结构图

设单极性二值逻辑开关函数为

在三相静止坐标下，基于基尔霍夫电压定律写出系统方程：

(2)

对于一个三相对称系统，有：

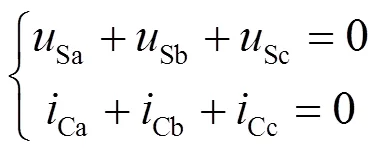
联立式(1)—式(3)，可以得到

(4)

2 滑模控制器设计

设计滑模变结构控制包括两个相对的部分：1) 设计合适的滑模面，产生稳定的滑模动态；2) 设计控制函数，在切换面上形成滑动模态区，使正常接近段的运动品质得到提高。函数和一旦设计好，就能建立起滑模变结构控制系统[6]。

在三相对称系统中，取a相进行分析。令状态变量：

可得状态方程为

(6)

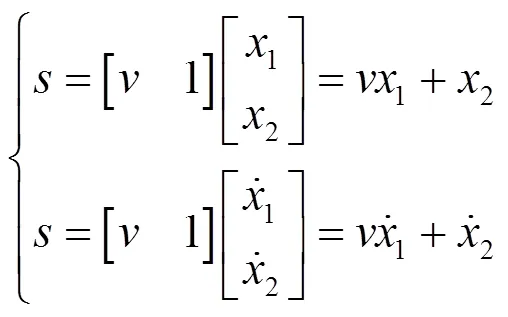
式中，为常数。

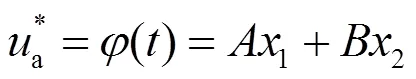
由可达性条件

(9)

推导出：

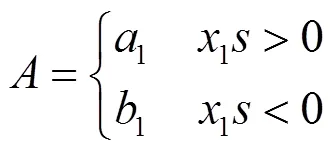
(10)

推导出控制函数参数应满足：

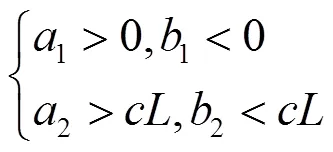
3 遗传算法优化控制器参数

在理想的情况下，滑模控制的状态点才会沿着滑模面滑动。一般在建模时，高频部分被忽略。开关切换容易引起系统抖动，抖动可能进一步激发在建模中被忽略的高频动态。高频抖动会对传感器造成影响，造成系统结构破坏或者控制失稳。本文通过遗传算法对滑模控制器参数进行优化确定，理论性强，减少传统试凑法确定参数花费的时间，提高效率，对控制效果也有提升。

3.1 遗传算法的优点

与传统的优化方法相比，遗传算法具有收敛性好，计算时间少，鲁棒性好等优点，在工程研究领域得到广泛应用。该算法搜索空间大，全局搜索能力强，可以快速得出全体解，搜索过程不易陷入局部最优解的快速下降陷阱[7]。

3.2 遗传算法的构造与改进

适应度函数值大的个体将有更多的机会生成新种群，得到函数值的最大解，然而电流控制器参数优化是寻找目标函数的极小值[8]。因此在个体适应度为时，构造适应度函数。为了取得最优的动态特性，将电流误差绝对值对时间的积分定义为目标函数，根据目标函数的最小值来选择参数。定义目标函数

本文结合退火算法，将适应度函数适当扩展，在后期增大个体间差异，避免产生过早收敛，解决遗传算法在局部搜索能力方面的不足。该算法采用如下的拉伸方法。

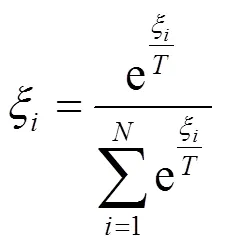
(14)

遗传算法能够很好地维持搜索深度和搜索广度之间的平衡。选择机制来深度搜索积累的信息，遗传算子来广度搜索解空间中新的区域。

对于选择机制，本文将竞争选择和轮盘赌选择结合，将高适应度的染色体进行繁殖，然后采用轮盘赌选出染色体对，将其中具有高适应值的个体带入新种群，直到满足新种群数量为止。随算法运行精英个体数量得以保证，在提高收敛速度的同时能有效防止算法陷入局部最优[9]。

遗传算子包括交叉算子和变异算子。交叉算子的性能很大程度上决定了遗传系统性能，将种群中个体的每个字符都作为潜在的交叉点进行选择[10]。而变异算子通常被用作次要算子，能改善遗传算法的局部搜索能力[11]。

3.3 控制器设计结果

取30个样本，式(15)中30为进化代数；0.8为交叉算子；0.1为变异算子。

测试函数经过30代遗传后，仿真结果如图2所示。仿真结果显示在经过遗传算法30代迭代后，在(4.9989,4.9865)处取得函数最小值-25.6876，也就是最大适应度，非常接近全局最优解的理论值，表明构造的遗传算法是可行的。

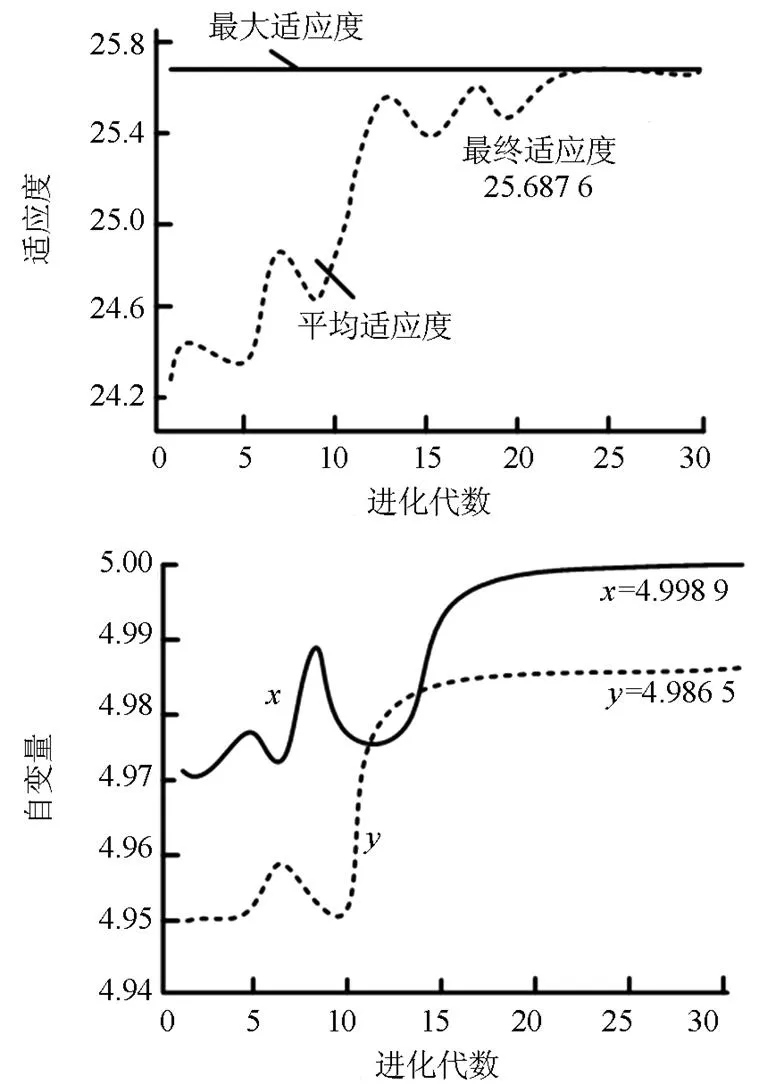
图2 测试函数仿真结果

4 实验分析

4.1 系统仿真

对三相并联型APF进行Matlab/Simulink仿真实验。实验条件为：电网线电压380 V，=50 Hz；交流侧电感a=b=c=20 mH；取三相整流电路为非线性负载，电阻=15 Ω，电感=3 mH。在控制参数相似的条件下将基于遗传算法的滑模控制器和传统的PI控制进行实验验证，分析其动态响应和稳态性能。以A相电流为例，仿真实验负载电流波形及频谱分析如图3，负载电流中含有大量次谐波，总的谐波畸变率()为28.83%。

使用滑模控制时，并联型有源滤波器动态性能明显改善，而且也取得了良好的补偿性能，跟踪性能好，电流毛刺比较小。系统稳定时，网侧电流接近理想正弦波形，滑模控制具有明显的优越性。

图4是传统PI控制方式和基于遗传算法优化后的滑模控制方式补偿后的电源电流波形，从波形的对比中可以看出，两种控制方式均可实现谐波电流补偿功能。传统PI控制方式在波峰与波谷电流变化率较小的点抖振现象严重，高次谐波大，波峰处最大抖振幅值达0.5 A，补偿后电源波形仍存在较明显畸变；而基于遗传算法优化后的滑模控制方式在波峰处最大抖振幅值小于0.2 A，有效削弱了抖振，补偿后电流波形正弦度较高。

图4 两种方式控制A相电源电流波形对比

图5所示为两种方案补偿后电源电流频谱分析。传统PI控制方式为4.58%，优化后的滑模控制方式为2.36%，均达到国标要求。但在相同条件下，后者补偿后电流低次谐波含量少，能有效降低畸变率，补偿效果更优。

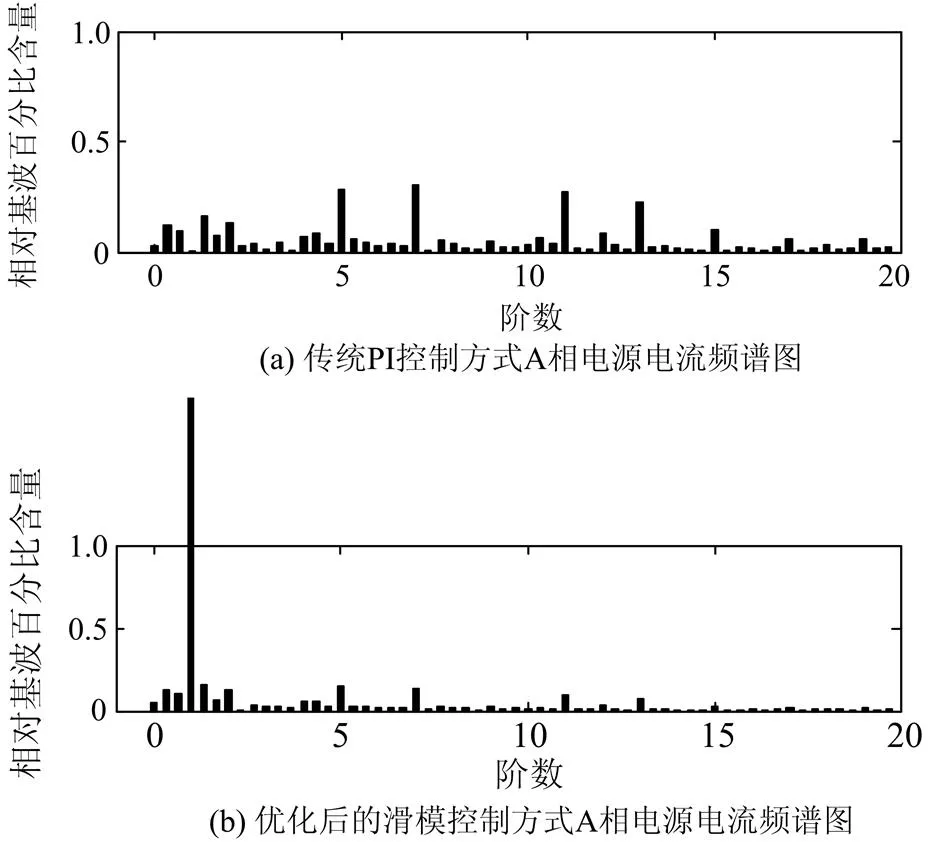
图5 两种方法控制A相电源电流频谱对比

采用优化后的滑模控制方式跟踪补偿谐波电流，在0.1 s时刻负载突变，补偿后的电源电流如图6所示，新的控制方式也能保证较快的动态响应。

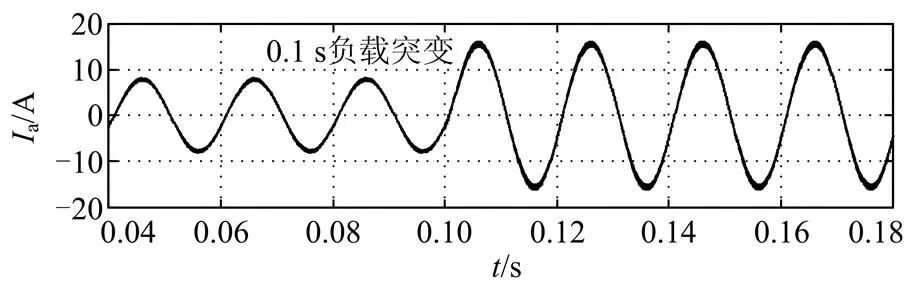
图6 负载突变优化后的滑模控制方式的A相电源电流波形

4.2 实验验证

为验证设计效果，以实验室低压三相并联型有源电力滤波器试验台为基础，以TMS320F28335为主控芯片，开关频率为10 kHz，实验主要参数和仿真参数基本相同。图7为A相负载电流波形与采用遗传算法优化的滑模变结构控制后的A相电源电流波形，补偿后近似成正弦波，证明所设计控制器对于谐波有较好的跟踪补偿效果[12]。

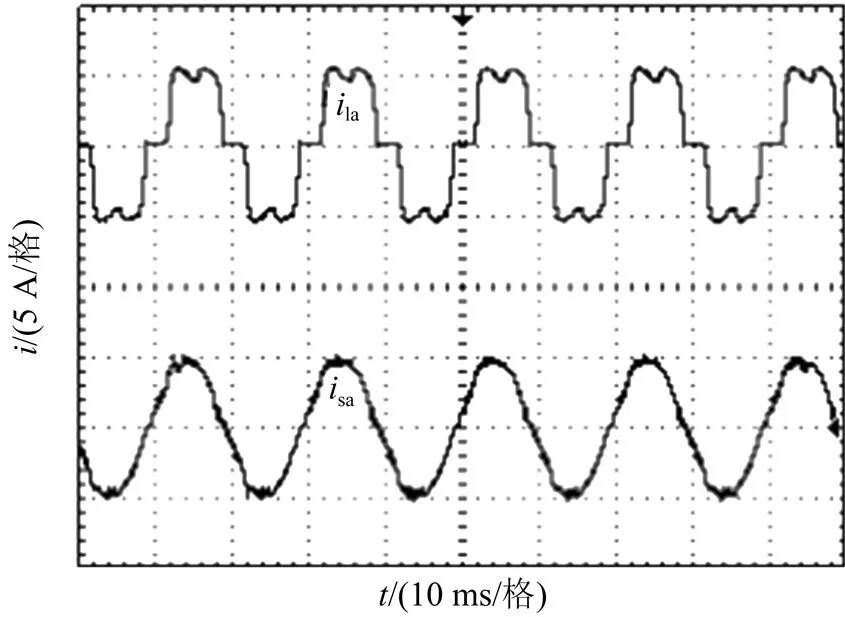
图7 A相负载电流波形与补偿后A相电源电流波形

为验证控制器动态性能，系统运行过程中出现负载突变。如图8所示，结果与仿真分析相同，系统经过短暂的波动后即进入新的稳态，暂态过程中电流未出现突变，控制效果较优。

图8 突变负载A相电流波形与补偿后A相电源电流波形

从实验结果看出，采用优化后的滑模控制时，并联型有源滤波器动态性能明显改善，而且也取得了良好的补偿性能，跟踪性能好，电流毛刺比较小。系统稳定时，网侧电流接近理想正弦波形。

5 结论

为改善有源电力滤波器在高频处抖动、系统响应时间以及抗扰动性能，本文提出一种基于遗传算法的滑模控制方式有源电力滤波器。运用遗传算法对控制器进行参数优化，理论性强，弥补了滑模控制参数试凑费时费力的缺陷。传统PI控制器与优化后的滑模控制器的对比实验表明，优化后的滑模控制器更能满足有源电力滤波器在快速性、鲁棒性方面的要求。所提出的控制策略是可行的，具有较好的理论和实用价值。

[1] 王兆安, 黄俊. 电力电子技术[M]. 北京: 机械工业出版社, 2005.

[2] 刘建华, 朱蓓蓓, 张亚健, 等. 有源电力滤波器相电流互感器容错控制[J]. 电力系统保护与控制, 2015, 43(20): 90-96.

LIU Jianhua, ZHU Beibei, ZHANG Yajian, et al. Fault-tolerant control of phase current transformer for active power filter[J]. Power System Protection and Control, 2015, 43(20): 90-96.

[3] 王玲, 冯宇, 邱进, 等. 电压互感器谐波特性测量用可控谐波电压源的构建[J]. 电力系统保护与控制, 2015, 43(16): 106-111.

WANG Ling, FENG Yu, QIU Jin, et al. Construction of controllable harmonic voltage source for harmonic characteristic measurement[J]. Power System Protection and Control, 2015, 43(16): 106-111.

[4] 高为炳. 变结构控制的理论及设计方法[M]. 北京: 科学出版社, 1998.

[5] 王烨, 牟宪民, 齐琛. 三相电流源型STATCOM的无锁相环控制策略[J]. 电力系统保护与控制, 2015, 43(14): 131-136.

WANG Ye, MU Xianmin, QI Chen. A control strategy of three-phase current source converter based STATCOM without PLL[J]. Power System Protection and Control, 2015, 43(14): 131-136.

[6] 曹武, 刘康礼, 赵剑锋. 有源滤波输出限幅的需求分析和实现策略[J]. 电工技术学报, 2015, 30(14): 405-411.

CAO Wu, LIU Kangli, ZHAO Jianfeng. The analysis of the conditions in which APF need output-limitation and its implementation scheme[J]. Transactions of China Electrotechnical Society, 2015, 30(14): 405-411.

[7] 王文, 罗安, 黎燕. 三相四开关并联有源电力滤波器的控制方法[J]. 电工技术学报, 2014, 29(10): 183-190.

WANG Wen, LUO An, LI Yan. Control method of three-phase four-switch shunt active power filter[J]. Transactions of China Electrotechnical Society, 2014, 29(10): 183-190.

[8] 李锰, 王志刚, 王寅, 等. 无谐波检测环节的并联型有源电力滤波器研究[J]. 高压电器, 2014, 50(10): 22-28.

LI Meng, WANG Zhigang, WANG Yin, et al. Shunt active power filter based on non-harmonic detection technology[J].High Voltage Apparatus, 2014, 50(10): 22-28.

[9] 侯睿, 武健, 徐殿国. 并联有源滤波器LCL滤波器特性分析及设计方法[J]. 电工技术学报, 2014, 29(10): 191-198.

HOU Rui, WU Jian, XU Dianguo.Characteristics and design methods of LCL filter in shunt active power filter[J]. Transactions of China Electrotechnical Society, 2014, 29(10): 191-198.

[10] KIM Y J, AHN S J, HWANG P I, et al. Coordinated control of a DG and voltage control devices using a dynamic programming algorithm[J]. IEEE Transactions on Power Systems, 2013, 28(1): 42-51.

[11] 王亮, 王志新, 陆斌锋, 等. 基于LCL滤波器的单相光伏并网逆变控制器设计[J]. 电网与清洁能源, 2014, 30(12): 114-118.

WANG Liang, WANG Zhixin, LU Binfeng, et al. Design of the controller of the single phase PV grid-connected inverter with LCL filter[J].Power System and Clean Energy, 2014, 30(12): 114-118.

[12] 游力, 陶骞, 代少君, 等. 一种应用于高压系统的有源电力滤波器的研究[J]. 电力电子技术, 2013, 47(9): 52-54.

YOU Li, TAO Qian, DAI Shaojun, et al. Research on the active power filter applied into high-voltage system[J]. Power Electronics, 2013, 47(9): 52-54.

(编辑 周金梅)

Sliding mode control of active power filters based on genetic algorithm

ZHANG Dongliang, XIE Yehua, LIU Juan, HUANG Kai

(School of Information and Electrical Engineering, China University of Mining and Technology, Xuzhou 221008, China)

The parameters of the controller are optimized by genetic algorithm, in order to improve the control method of active power filter in defects at the high frequency chattering of the sliding mode and the controller performance. The principle of three-phase three wire active power filter is introduced and the design of the optimization of controller parameters of genetic algorithm is analyzed in detail. The exact values of the parameters of the controller are achieved. According to the error of the compensation current and instruction current, sliding mode variable structure controller is obtained. Though the simulation of experiment of the traditional PI control method and the optimized sliding mode control, the results demonstrate that the proposed method can obtain quick response, simple algorithm and better jitter suppression and robustness. This work is supported by Natural Science Foundation of Jiangsu Province (No. BK20130187).

active power filter; sliding mode control; genetic algorithm;parameter optimization;robustness

10.7667/PSPC150764

江苏省自然科学基金青年基金(BK20130187)

2015-05-08；

2015-11-05

张栋梁(1974-)，男，博士,副教授，研究方向为电气安全、电能质量控制及有源滤波器等；谢业华(1989-)，男，通信作者，硕士在读，研究方向为电能质量；E-mail: 969460929@qq.com 刘娟(1989-)，女，硕士在读，研究方向为电气安全和城市轨道交通研究。