基于希尔伯特黄变换的频分编码声信号识别算法
中北大学信息探测与处理技术研究所 李 凯 郑长海
基于希尔伯特黄变换的频分编码声信号识别算法
中北大学信息探测与处理技术研究所 李 凯 郑长海
【摘要】在声定位系统中信源的识别是需要解决的一个问题,对此提出了一种频分编码方式。该编码由特征信号段和信源标识信号段。信号编码的长度固定,特征信号的频率及长度固定,同时在编码中的位置固定。那么针对这种频分编码,提出了一种基于希尔伯特黄变换的识别算法。通过对实际采样信号的分析处理已验证该方法能准确的分辨声源,同时能比较准确的定位信号的位置从而减小盲区。
【关键词】频分编码;声定位;希尔伯特-黄变换
0 引言
目前,声定位技术主要应用于水声定位和近地炸点定位。其基本都是采用时差法进行定位。而目前还缺乏利用固定声源对各声传感器的位置进行定位的应用研究,虽然在陆地上可以利用GPS进行定位,但是一般的GPS定位精度低,对于高精度的GPS定位需要在地面建立基站,成本大[1]。在爆炸试验中,冲击波传感器的节点很多。为此设计出一套定位系统。该系统以喇叭作为发声源,在进行试验时把声接收装置分布在冲击波传感器及炸点所在的位置,从而通过一定的算法来确定冲击波传感器和炸点的位置。而本算法是为了解决定位系统中信源的识别,同时减小盲区。根据信源(喇叭)发声的实际特性,提出频分编码方式[2],同时给出了具体的识别算法。
1 声信号的编码
本文给出的编码方式是由两部分组成:特征信号段和信源标识信号段。编码的时间长度是固定的,特征信号段的时间长度和在编码中的位置是固定的。具体信号编码的特征如图1所示。
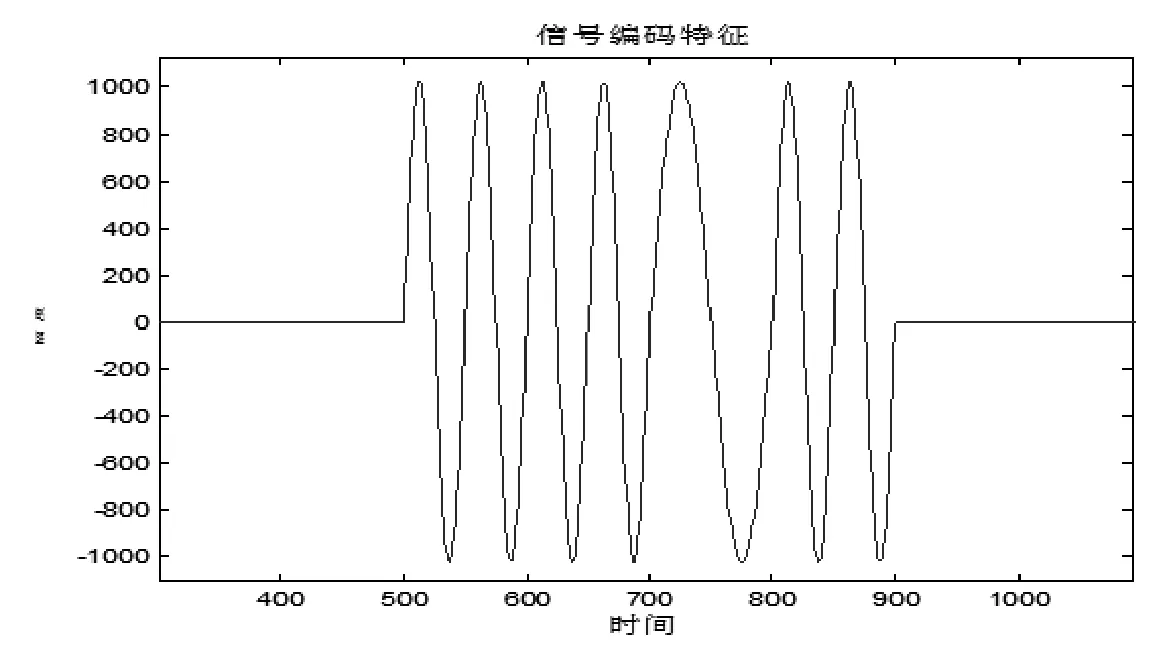
图1 信号编码特征
2 HHT在编码声信号识别中的应用
HHT是一种通过计算信号的瞬时频率来分析信号的计算方法,它是通过先对非线性非平稳信号进行EMD分解得到瞬时频率有实际物理意义(Physical Meaningful)且逐级分布、能反映信号内部震动模式的一组单一分量IMF,然后对分解获得的IMF进行希尔伯特变换,最终利用变换的结果来分析信号。
因此本算法第一步,是对采集的编码声信号进行EMD分解。EMD过程的合理性和有效性是基于以下两点。
EMD是 HHT 的关键步骤,可以视为获取IMF的筛选过程(Sifting Processing)。EMD过程的合理性、有效性基于以下两点:
(1)任何复杂信号 s(t)都可以表示成n个瞬时频率有实际物理意义、可非正弦波信号的单分量imfk(t)的叠加,即:

其中imfk(t),k=1,2,...,n,是否满足线性性并不做要求,rn(t)为残余分量
(2)筛选的终止条件:该信号相对于局部零均值线对称,且极值点与零穿越点有相同的数目。
EMD分解的步骤如下[3]:
1)找出s (t)的所有极大值点Maximum-set和极小值点Minimum-set。
2)用Maximum-set拟合s(t)的上包络u(t),用Minimum-set拟合s(t)的下包络 l(t)。
3)计算 s(t)局部均值 m(t) = (u(t) + l(t))/2。
4)去均值: h(t) = s(t) − m(t)。
5)判断h(t)是否满足IMF定义?,如果不满足,s(t)=h(t),返回步骤1,如果满足,记imfi(t)=h(t),i=1,2,3,...,n,判断是否满足rn(t)为一个单调函数,不再能筛选出任何IMF分量?如果不满足,s(t)=s(t)-imfi(t),返回步骤1,如果满足,结束。
第二步,得到一组IMF分量之后,对IMF分量进行希尔伯特变换,其计算方法如下[4]:
对于任意给定一个时间序列信号X(t),总是可以得到它的 HT 结果 Y(t),如下:
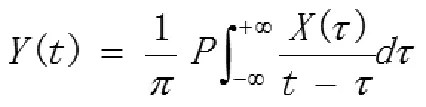
其中P 表示柯西主值(Cauchy Principal Value),HT对于所有Lp类函数都存在。通过这个定义,将 X(t)、Y (t)形成一个复数共轭对,来定义一个解析信号 Z(t):
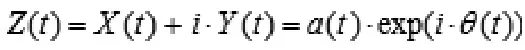
于是可以推出如下的瞬时频率计算公式:

通过以上的计算我们就可以得到每个单模式分量信号的瞬时频率和幅值。

图2 实验采集信号

图3 EMD分解结果
第三步,通过比较每个信号分量瞬时频率的幅值,以幅值最大确定瞬时频率。然后给定一个频率区间对瞬时频率进行量化,通过量化后的时频分布图来确定信号的类型,根据量化后但频率信号连续持续的长短来确定信号的位置。这样就可以识别信源,同时本算法由于对信号的定位比较准确。
3 实验数据分析
下面我们以实际所采信号为例验证该算法的可行性。
实际信号如图2所示。
实验采样信号中包括两个信号,信源标识频率依次是3.072k、4.608k,两组信号距离大致相差10ms,对采集信号进行EMD分解后的结果如图3所示。
采样信号时频分布图及量化结果如图4所示。

图4 时频分布及量化结果图
从图4中可以看出信源标识段的频率总体分布在一个信号标识频率附近,在信源标识段中存在一些频率跳跃点,为了缩小量化频率所需的频率带宽,因此需要对时频分布图进行平滑处理,消除这些跳跃点。在消除跳跃点后对信号进行量化。量化后可以看出信源标识段的频率的时间长度比非信号区明显宽,两段不同频率的信号可以明显的区分出来,因此本算法能很好的识别不同信源,同时能减小因为信号太近而产生盲区。
4 结论
由实验结果可知,基于希尔伯特黄变换的频分编码声信号识别算法,实现简单,能够比较准确的识别信源。完全能满足定位系统的要求,具有很高的应用价值。
参考文献
[1]Rycroft.M.J.Understanding GPS,Principles and Applications[J].Journal of Atmospheric and Solar-Terrestrial Physics,1997;59(5):598-599
[2]戴萧嫣,韩焱.基于频分模式的水声自主定位[J].微计算机信息,2008,01:286-287+309.
[3]徐晓刚,徐冠雷,王孝通,秦绪佳.经验模式分解(EMD)及其应用[J].电子学报,2009,03:581-585.
[4]王宏宇.基于希尔伯特—黄变换的语音识别特征提取方法研究[D].华南理工大学,2012.

