电镍导电棒斜辊矫直机设计

童　切，孙东明，吴　琼，金　岩

(1.昆明理工大学 机电工程学院，云南 昆明 650500；2.金川集团股份有限公司 镍冶炼厂，甘肃 金昌 737100)



电镍导电棒斜辊矫直机设计

童切1，孙东明1，吴琼2，金岩2

(1.昆明理工大学 机电工程学院，云南 昆明 650500；2.金川集团股份有限公司 镍冶炼厂，甘肃 金昌 737100)

摘要：根据矫直理论，确定了电镍导电棒斜辊矫直机的相关参数，着重研究了斜辊矫直机的辊系和辊型。应用DEFORM软件进行了有限元数值模拟分析，比较了矫直前、后导电棒的波浪度，确定了较优压下量为0.5 mm。根据试验所得矫直效果(导电棒矫后波浪度均<1%)，验证了设计的可靠性。

关键词：导电棒；矫直；斜辊；DEFORM

由于镍的导电性比铜弱，某企业在镍的电解精炼过程中，采用紫铜圆管(尺寸为φ36 mm×3 mm×1 350 mm)作为导电棒，有效加强了与吊耳的接触。但是，导电棒会因为长期使用或受外力作用而变弯扭曲，从而直接影响镍的实际生产。过去依靠人工对其进行矫正，效率低，效果差，噪声大，劳动强度也大，并且大量的导电棒由于变形严重而被报废处理，造成了经济上的损失。

针对导电棒采用紫铜圆管，决定采用斜辊矫直机。斜辊与平行辊相比，能矫直各方位的纵向剖面弯曲，避免了因导电棒自转而产生的螺旋形弯曲[1]。设计适用的矫直机，不仅可以减小劳动强度，实现生产自动化，而且能提高导电棒重复利用率，产生一定的经济效益。

1矫直机设计

实际生产过程中导电棒的弯曲往往集中在中间部位，而且有可能是多方位弯曲，因此， 本文采用六辊辊系(见图1a)。六辊同时绕OO′轴旋转，可以实现导电棒各方位的交错压弯，达到矫直的目的；另外，六辊辊系克服了传统辊系各辊之间存在的速度差缺陷。与老式222辊系相比， 采用中间对辊交错布置可以适当延长塑性变形区。由于镍电解精炼过程中对导电棒的精度要求并不是特别高，而新式222辊系中间凸凹辊用力大，易产生过载压弯现象，也不予采用。

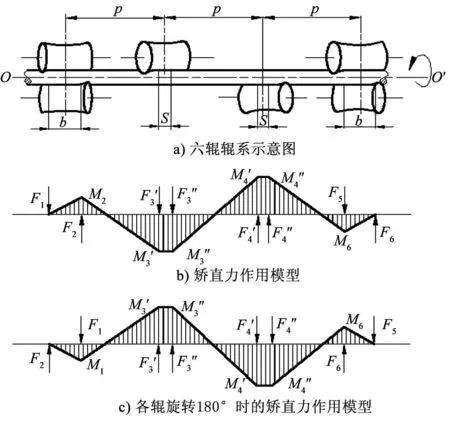
图1　斜辊矫直机辊系

当矫直机各辊处于图1a所示的位置时，矫直力作用模型如图1b所示；而当矫直机各辊旋转180°时，矫直力作用模型如图1c所示。其中，p为辊距，b为固端区长度，S为等弯矩区长度。以图1c为例，矫直力计算公式如下：

本文研究的紫铜圆管尺寸较小，故采用小规格的矫直机就能满足要求。导电棒与斜辊的关系模型如图2所示。辊腰直径Dg、辊长L、辊子斜角α、辊距p、矫直速度v和压下量y为矫直机的基本参数，对矫直效果、能耗和结构尺寸等均有影响(由于椭圆度对导电棒影响较小，先不重点考虑压扁量的作用)。

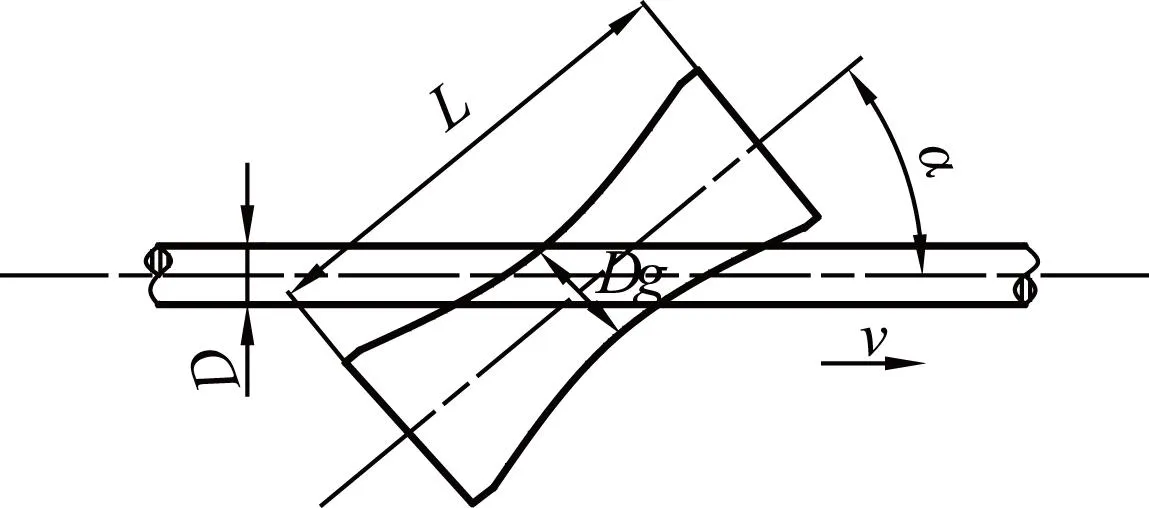
图2　导电棒与斜辊的关系模型

辊腰直径Dg≥(2～3)D(D是导电棒直径)，辊子全长L=(1.5～2.5)Dg；辊子工作部分长度Lg=(0.8～0.9)L；辊距p=(1.5～2.5)L；压下量y=(0.64～0.77)σtl2/6ED[2-3](σt是规定总延伸强度；l是矫直辊的支承距离l=2p；E是弹性模量)。

导电棒材料为紫铜，弹性模量E=125 GPa，规定总延伸强度σt=100 MPa，因此，取辊腰直径Dg=2D=72 mm，辊长L=2Dg=144 mm，辊子工作部分长度Lg=0.85L=122.4 mm，辊距p=1.5L=216 mm，辊子斜角α=40°。考虑到企业生产效率、矫直机工作稳定性以及动载荷的影响，选取矫直速度v=1 000 mm/s。

在斜辊矫直机的设计中，矫直辊辊型曲线是重要参数，影响着矫直效果。合理的辊型能对导电棒具有良好的包裹性，实现近似的完全接触，保证矫直过程中导电棒受力均匀、运转稳定。导电棒直径D、辊腰直径Dg和辊子斜角α决定了辊型曲线。当被矫件直径发生变化时，通过调整辊子斜角α来实现更好的接触。目前，国内外学者对于辊型设计做了大量研究，其中，较为常见的一类设计思想是假设被矫件为理想的平直管材。另一种设计考虑了实际情况中被矫件存在弹塑性弯曲，这种设计方法得到的辊型更贴合实际，矫直效果更好；但是，过多依靠实践经验，公式复杂，难以求证，在工程中运用较为困难[4]。考虑到该型矫直机压弯量不大，决定采用基于理想条件下的解析法。赵炳利推导出的辊型计算公式为[5]：

(1)

式中，r0是管材半径；c0=r0+R0；R0是辊腰半径；ci=zitanα，zi是辊型曲线上某一点与矫直辊对称中心的轴向距离，对应的矫直辊半径为Ri。

式1经过适当修正，得到辊型曲线坐标(见表1)。

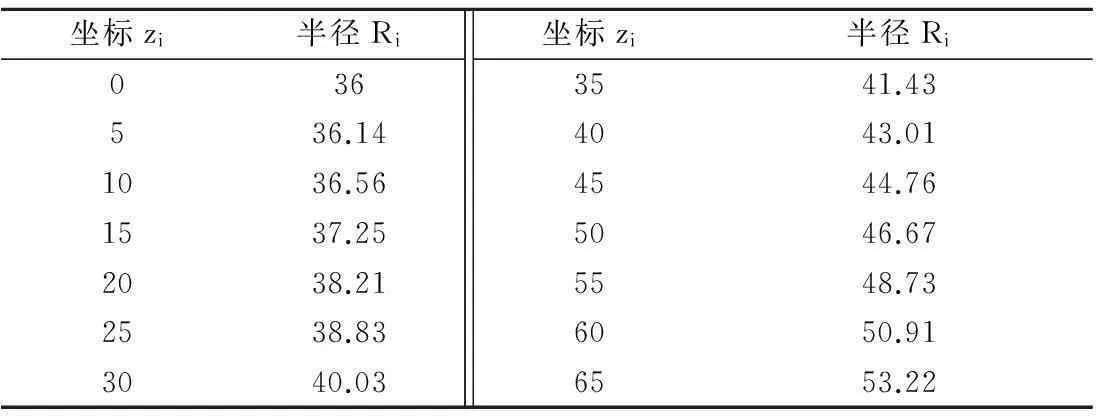
表1　矫直辊辊型曲线坐标　(mm)

2数值模拟分析

由于紫铜没有明显的屈服平台，存在加工硬化现象，故将导电棒视为理想的弹塑性材料。矫直辊相对导电棒刚度较大，将其视为理想的刚性材料。建模时，导电棒长度为1 350 mm，引入初始弯曲挠度为30 mm，即波浪度Δ=H/L×100%=30/1 350×100%=2.22%。按照上述结果设置矫直机参数，建立的模型如图3所示，中间2辊分别引入0.5、0.75和1 mm等3种压下量进行比较，其中，平行辊起到输送和粗矫的作用。

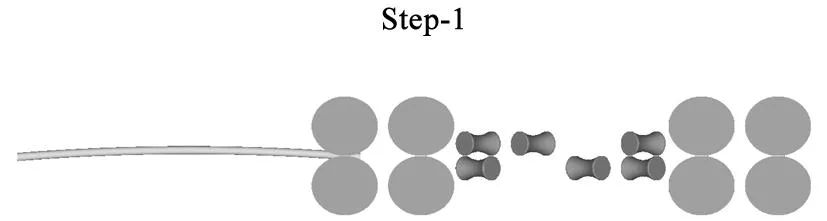
图3　有限元模型

以压下量0.75 mm为例，斜辊对导电棒的咬入、稳定矫直、抛出和矫后情况如图4所示。从图4可以看出，导电棒塑性变形主要发生在稳定矫直阶段，且变形区主要集中在导电棒中间部分，两端存在矫直盲区，与实际相符，验证了理论。通过对比导电棒矫前和矫后发现，弯曲程度得到明显改善。

图4　矫直各阶段的等效应力图和矫后效果图

矫直后，横向导电棒最上方均匀布置的10个节点的坐标如图5所示。

图5　不同压下量时的节点坐标

根据波浪度Δ=(H/L)×100%=(L4/L1)×100%计算得到：当压下量为0.5 mm时，Δ=0.093%；当压下量为0.75 mm时，Δ=0.219%；当压下量为1 mm时，Δ=0.239%；均满足精度要求。其中当压下量为0.5 mm时，矫直效果最好。

3实际矫直效果分析

通过矫直理论，设计出矫直机相关参数，再利用数值模拟分析，得到相对较优压下量；但工程实际情况相比理论更为复杂，能否在实际加工中获得好的矫直质量是设计的根本。在现有斜辊矫直机的基础上，进行适当改造，使其符合设计要求。再对导电棒进行矫直试验，对比分析矫直前、后的波浪度和表面压痕、磨损，评估矫直效果，验证设计是否可靠。

随机抽取100根导电棒，分10组进行试验。利用直尺和工作平台测量导电棒矫直前、后的弦高H和弦长L，计算得到弯曲曲率ρ=8H/(L2+H2)和波浪度Δ=H/L×100%。各组矫直前、后弯曲曲率和波浪度均值如图6所示。

从图6可以看出，矫直前、后导电棒弯曲曲率和波浪度存在明显变化，矫后波浪度均<1%，能够满足生产需求。矫后导电棒的椭圆度改变不大，表面压痕、磨损等对实际生产也影响甚微，证明该设计是合理的。而试验得到的波浪度较模拟仿真结果大，主要有两方面原因：1)导电棒使用时间长，已不是理想材料，弹性发生变化；2)机器精密度、施工条件存在差异性，测量也有一定误差[6]。

图6　矫直前、后弯曲曲率和波浪度均值

4结语

根据上述分析，可以得到下述结论。

1)根据实际导电棒的弯曲特点和生产中对其精度的要求，采用了新式矫直机辊系。与以往辊系相比，克服了存在速度差等缺陷，更符合电镍导电棒实际矫直需求，更贴合实际。

2)针对矫直该型导电棒所需压下量较小的情况，基于理想条件设计了矫直辊辊型曲线。但在实际生产中，使用该方法得到的辊型曲线过弯，在进行适当修正后，能与导电棒更好接触。

3)在有限元数值模拟分析中，使用理论设计参数设置矫直机。当压下量为0.5 mm时，矫后波浪度为0.093%；当压下量为0.75 mm时，矫后波浪度为0.219%；当压下量为1 mm时，矫后波浪度为0.239%。压下量为0.5 mm时的矫直效果相对更佳。

4)通过试验样机得到导电棒矫后波浪度均<1%，证明设计可靠。但试验得到的波浪度比数值模拟的大，主要是因为导电棒长期使用，弹性降低以及试验条件与理论存在差异。

参考文献

[1] 崔甫.矫直原理与矫直机械[M].北京:冶金工业出版社,2002.

[2] 李连进.六辊斜轧无缝钢管矫直机的压下量研究[J].锻压技术, 2008,33(5):82-84.

[3] 杨晓臻,赵志毅,孙林. 8mm厚高强钢板矫直策略的模拟仿真研究[J].新技术新工艺, 2015(7): 106-109.

[4] 郑焕平.大口径钢管斜辊矫直的工艺理论及数值仿真研究[D].秦皇岛:燕山大学, 2011.

[5] 赵炳利,徐燕,于敏之.管材矫直机的辊形设计[J].一重技术,1996(1):39-41.

[6] 潘东亮.电铜导电棒矫直工艺参数研究及矫直效果分析[D].昆明:昆明理工大学, 2014.

责任编辑郑练

Design of Cross-roller Straightening Machine for Electrolytic Nickel Conducting Bar

TONG Qie1, SUN Dongming1, WU Qiong2, JIN Yan2

(1.Faculty of Mechanical and Electrical Engineering, Kunming University of Science and Technology, Kunming

650500, China; 2.Nickel Smelter, Jinchuan Group Co., Ltd., Jinchang 737100, China)

Abstract：Based on the straightening theory, design the relevant parameters of cross-roller straightening machine for electrolytic nickel conducting bar. It focuses on the roller system and roller shape. Take finite element numerical simulation analysis by using DEFORM software, get the wave of conducting bar after straightening, then determine the optimal reduction. Finally, verify the reliability of the design according to the straightening effect from experiments.

Key words:conducting bar, straightening, cross-roller, DEFORM

收稿日期：2015-08-31

作者简介：童切(1988-)，男，硕士研究生，主要从事机电产品开发与创新等方面的研究。

中图分类号：TG 333.2+3；TH 12

文献标志码:A