某型发动机任务备件需求研究
苗 磊
(海军91049部队,山东 青岛 266102)
某型发动机任务备件需求研究
苗磊
(海军91049部队,山东 青岛 266102)
摘要:针对备件短缺影响发动机完好率的问题,在分析发动机可靠性的基础上建立了非齐次泊松过程的备件需求计算模型。通过算例分析,对某型发动机备件数量进行了计算。结果表明,该模型能够对发动机备件需求的数量进行准确计算,对执行任务的该型飞机所需携带备件数量具有较好的实际指导作用。
关键词:发动机;备件需求;非齐次泊松过程
在外场维护时,发动机部件发生故障后能否及时得到替换对于提高发动机的完好率是非常重要的。经常执行远洋护航任务的某型飞机发动机,每架次任务飞行时间约为100 h,那么,每次执行任务时,该型发动机应该配备多少备件才能保证飞机具备较高的战备完好率,是一个需要研究解决的重要问题。本文在分析某型发动机故障规律的基础上,针对某型直升机经常随舰出海执行任务的特点,对所需携带发动机备件进行定量研究,为部队圆满完成任务提供决策支持。
1发动机故障规律分析
对于修复性维修所需备件,目前比较常用的方法是利用泊松过程的原理进行数量确定。满足泊松过程应符合3个条件[1]:1)产品故障数量与时间起点无关,只与时间长短有关;2)产品在很短的时间内发生2次以上的故障事件的概率几乎为零;3)产品发生的不同故障是相互独立的。发动机备件数量的确定应满足上述条件,因此,可以利用泊松过程原理对发动机备件数量进行确定。
发动机是可修复系统,由于发动机发生故障的时刻是随机出现的,可以把它看成是时间轴上依次出现的随机点,所以,可用随机点过程来描述发动机的故障过程。用于描述可修复系统的随机点过程模型通常有3种:齐次泊松过程、由齐次泊松过程推广的更新过程和非齐次泊松过程。
齐次泊松过程是基于故障强度函数等于常数的假设,对发动机而言,由于部附件劣化等原因,这一假设显然不适合发动机故障过程。更新过程只可用于描述“修后如新”的可修系统的运行特征,而大多数发动机维修只涉及到更换一小部分系统的零件,即使维修使系统功能恢复到原来的水平,但系统的可靠度并没有更新。非齐次泊松过程先后被称为“最小维修”和“修后如旧”,“修后如旧”是指机器产品修复后恢复了正常功能,但其状态与新产品并不完全一样。发动机的可靠度在维修后和故障前基本是一样的,非齐次泊松过程可作为发动机故障过程的可靠性模型;因此,本文采用非齐次泊松过程来对发动机所需备件数量进行建模计算。
目前,国家军用标准和各种文献中提供的备件数量确定方法是根据产品的故障率来计算的[2]。本文采用非齐次泊松过程模型结合发动机部附件故障率来计算发动机在任务期间所需备件数量。
2基于非齐次泊松过程的备件需求计算模型
2.1非齐次泊松过程简介
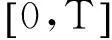
对于事件累积强度函数Λ(t)有如下的形式:
(1)
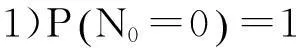

3)有独立增量。
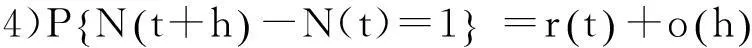


(2)
期望的事件数为:

(3)
2.2备件需求的计算模型
在应用非齐次泊松过程计算发动机备件需求量时,由于备件需求问题涉及因素众多,本文对此问题进行相应的简化与假设:主要研究在平稳状态下基层级备件的需求问题,并且不考虑飞机之间的串件修理对备件需求量的影响;所有故障都在外场使用过程中发生,故障件在外场可用备件更换;备件的缺货将导致发动机停飞;各部件的故障与备件的缺货的过程相互独立;发动机的保障率与备件的储备量相关。
在上述假设给定的前提条件下,本文建立了基于非齐次泊松过程的备件需求计算模型。备件需求量可采用随机点过程中的非齐次泊松过程,利用该方法不仅可以进行故障发生时间点以及时间间隔模拟,而且可以计算一定时间内故障次数的期望。
(4)
式中,α的值根据多年的数据统计经验来确定,也称其为保障率,其变化范围一般取85%~92%。
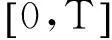

(5)
(6)
计算出来的n是根据故障率计算出来的航空装备的故障数。对于不可修件,是备件的需求量;对于可修件,是维修方式为最小维修时发生的故障次数。本文中,由于舰上不具备维修发动机部附件的条件,发动机所有件均作不可修件处理。
3备件需求算例分析
计算得出的起动电磁活门故障服从威布尔分布,故障率函数式为:
(7)
在护航时4台发动机总工作时间400 h、保障率为92%的条件下,由式6可计算出起动电磁活门的备件需求量。
由式1代入数据,得:
(8)
(9)
根据式8、式9,得到起动电磁活门备件需求个数随工作时间变化情况如图1所示。

图1 92%保障率下起动电磁活门备件需求量
从图1可以看出,发动机工作400 h所需起动电磁活门备件数为3个。按同样的方法,计算起动电磁活门在保障率为89%条件下的备件需求数(见图2)。

图2 89%保障率下起动电磁活门备件需求量
对比图1和图2发现,在保障率分别为89%和92%的条件下,所需备件数量几乎无差别,故统一采用92%的保障率计算其他备件的需求量。
磁性屑末检测器的故障时间服从正态分布,故障率函数表达式为:
(10)
磁性屑末检测器的备件需求量如图3所示。

图3 磁性屑末检测器备件需求量
放气活门的故障时间服从指数分布,故障率函数表达式为:
(11)
放气活门的备件需求量如图4所示。

图4 放气活门备件需求量
按此方法对发动机其他部附件的备件需求进行研究,计算出2架直升机执行任务时发动机总工作400 h所需备件数(见表1)。
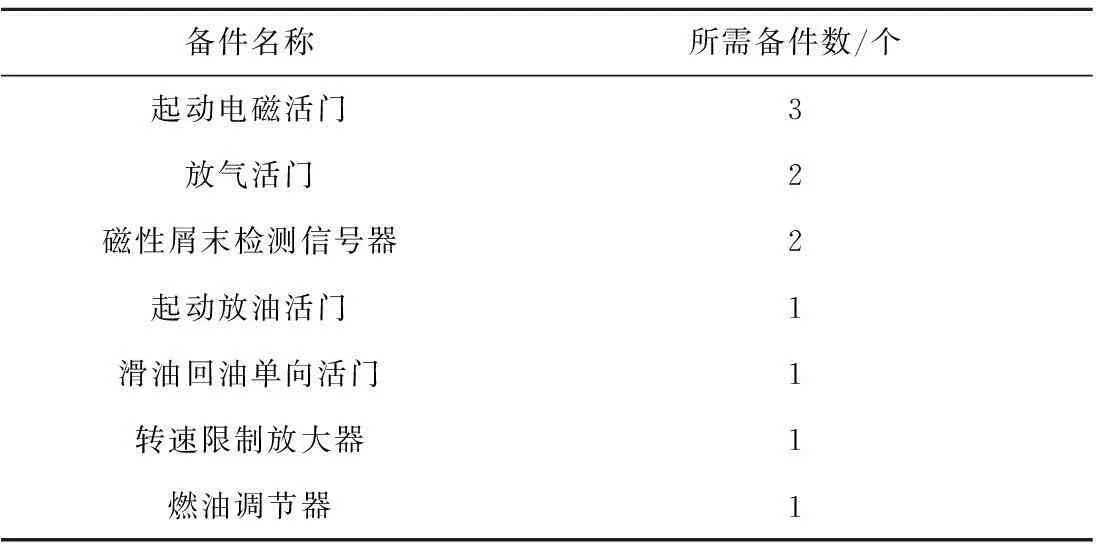
表1 发动机备件需求
4结语
本文通过分析发现发动机的故障发生时间服从非齐次泊松过程,基于此特性设计了一种基于非齐次泊松过程的备件需求计算模型,通过对起动电磁活门、磁性屑末检测器和放气活门的算例分析表明,该模型能够对发动机备件需求数量进行准确计算,可以应用于实际工作中。
参考文献
[1] 单志伟,刘福胜.备品备件需求确定方法探讨[J].装甲兵工程学院学报,2005,19(3):1-4.
[2] 陈凤腾,左洪福,王华伟,等.基于非齐次泊松过程的航空备件需求研究和应用[J].系统工程与电子技术,2007,29(9):1585-1588.
责任编辑郑练

The Investigation of Requirement of the Run Short of Spare Part for Certain Engineer
MIAO Lei
(Navy 91049 Unite, Qingdao 266102, China)
Abstract:According to the whole probability of certain engineer because of the run short of spare part question, the non-uniform Possion processing compute model of the run short of spare parts is founded based on reliability analysis of certain engineer. Through the analysis, the numbers of the run short of spare parts are computed. Through the results, we can find that this model can exactly compute the number of the run short of spare parts, this can provide preferable practice application value for practice with numbers of certain plane.
Key words:engineers, the run short of spare, non-uniform Possion processing
收稿日期:2015-08-31
作者简介:苗磊(1982-),男,大学本科,工程师,主要从事导弹发动机等方面的研究。
中图分类号:V 235.13
文献标志码:A

