基于角动量空间的SGCMGs姿态控制策略

梁金金，张小柯，宋效正，吕 旺

(上海航天技术研究院上海卫星工程研究所，上海201109)

基于角动量空间的SGCMGs姿态控制策略

梁金金，张小柯，宋效正，吕 旺

(上海航天技术研究院上海卫星工程研究所，上海201109)

针对单框架控制力矩陀螺(SGCMGs)的奇异问题，旨在建立一种基于角动量空间而非力矩空间的SGCMGs姿态控制策略，从根源上解决SGCMGs的操纵奇异，且不失其敏捷特性.由于此控制方案的动量管理环节需要另外一套动量交换机构参与，故引入反作用飞轮(RWs)组成混合执行机构，同时RWs可在机动末端用于高精度姿态稳定.针对双平行SGCMGs，采用特征轴时间最优路径进行角速度规划，并基于角动量空间设计控制策略.同时，针对一个陀螺失效的情况设计了相似的角动量控制算法.仿真结果表明，采用角动量控制律不涉及奇异问题，且敏捷性与稳定性良好.

操纵奇异;角动量空间;特征轴旋转;角动量管理

0 引言

目前SGCMGs奇异问题的解决主要基于两种思路，一是对陀螺群力矩矩阵的伪逆下功夫以寻求准确、可解的输出力矩，如添加零运动［1］、添加物理约束［2］、鲁棒伪逆［3］、奇异值分解［4］、混合操纵律［5］等方法，但伪逆解往往难以平衡准确性与可解性;二是引入其他执行机构补偿奇异方向力矩，如文献［6］用动量轮输出奇异方向力矩，但此方法需要在线进行奇异值分解，且没有完全利用SGCMGs的机动能力.

注意到以往的操纵律一般是围绕力矩指令的伪逆求解，而本文的控制算法只产生陀螺群角动量指令，再基于某种最优准则映射到SGCMGs框架角，就可以得到框架转速指令.可以证明(根据角动量体是框架向量的连续函数)，除非SGCMGs角动量体内存在空洞，否则不会出现奇异问题.

1 控制逻辑概述

本文总体控制思路如图1所示.

姿态控制分SGCMGs和RWs两条线，且两条线并行运作.机动阶段，SGCMGs提供机动所需的角动量，RWs进行整星的角动量管理(角动量管理使得星体角速度与SGCMGs角动量成比例关系);稳定阶段，将SGCMGs的角动量归零使其不影响飞轮姿控，最后利用RWs进行高精度姿态稳定.

姿态机动遵循特征轴最优时间路径，特征轴旋转为两个姿态间的最短角路径，而时间最优通过当前姿态下卫星可实现的绕特征轴最大角速度实现.

2 构型分析与角动量范数

本文控制算法宜用欧拉向量θ描述姿态运动，它是姿态阵特征值为1的特征向量［7］，其与四元数矢部关系为θ=q·θ/sin(θ/2)，θ为绕欧拉轴转角［8］.

经过角动量管理后角速度只由SGCMGs的角动量决定，当姿态误差为θ时，－θ方向的最大角速度与SGCMGs在Jθ方向的最大角动量相对应.为了表示陀螺群在任意方向下的最大角动量，引入角动量范数［9］定义(可以验证其满足向量范数三公理)

式中，u代表任意三维向量，HMax(u)是u方向上的最大角动量.角动量范数因构型而异，对于双平行构型其有解析表达式.

图2中，ObXbYbZb为星体坐标系，gi、si、ti(i= 1，2，3，4)分别为SGCMGs框架轴向、转子轴向及转子横向方向向量，三向量与框架坐标系三轴指向重合，且满足gi×si=ti.设陀螺转子标称角动量为Hw，可得图2角动量体.

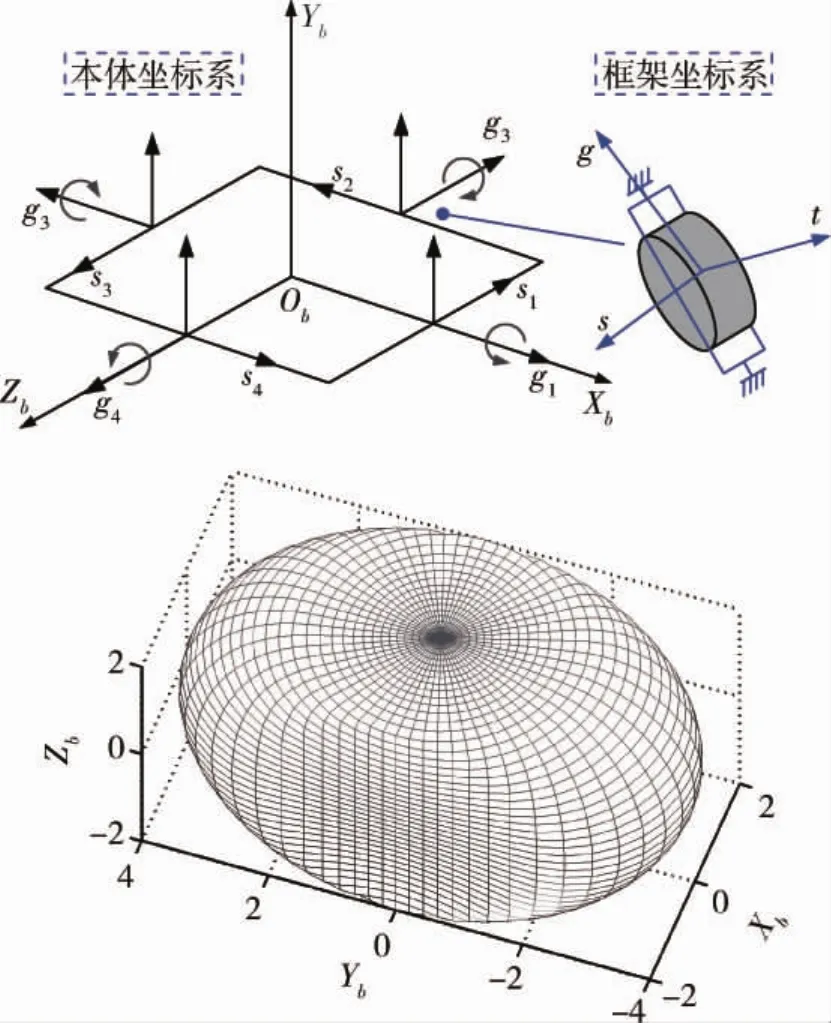
图2 双平行SGCMGs构型及角动量体Fig.2 Double parallel SGCMGs configuration and angular momentum-bounding envelope

由图2可知，陀螺2和4产生XbYb平面的角动量hxy;陀螺1和3产生YbZb平面的角动量hyz.两者最大值皆为2Hw.图2包络面分为平面部分和曲面部分，u的方向决定了HMax(u)是属于哪一部分.

包络面的平面部分指向±Xb与±Zb方向，原点与四个平面圆可构成四个圆锥，u在圆锥面内时其分量须满足≤－，此时角动量在Xb或Zb上分量达到饱和值2Hw，且由hxy或hyz提供，故有

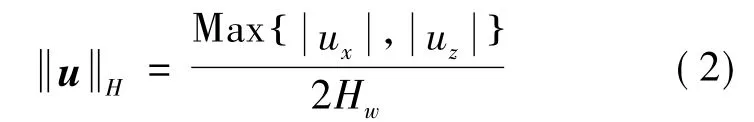
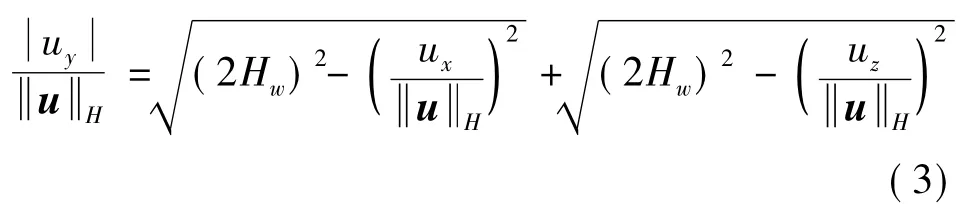
由上式可解出uH表达式.

综上，双平行SGCMGs的角动量范数表达式为

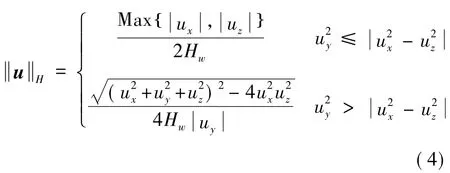
3SGCMGs控制策略

3.1 角速度规划

姿态为θ时可实现的最大角速度为

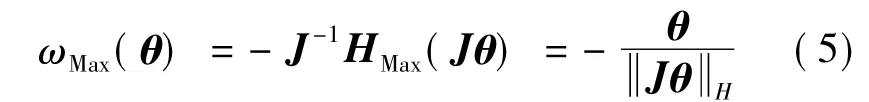
式中，JθH由式(4)定义.加速过程角速度曲线与框架角状态有关，没有统一表达式，故加速与匀速过程的参考角速度都是最大角速度.

关键是减速过程制动曲线的设计，须保证快和准.双平行构型的优势在于，每对陀螺在“剪刀式”运动过程中，双平行SGCMGs系统能以最短时间从最大角动量减至零动量，且保持方向不变.制动时，其角动量按框架角的余弦变化，即有

式中，ωR表示参考角速度，为最大框架转速，为0时制动开始，为π/2时制动结束角动量归零，对上式积分有

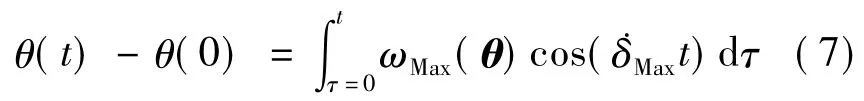
代入姿态归零边界条件，可得

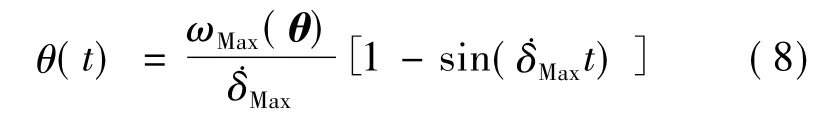
联立式(6)和式(8)，并代入式(5)结果有

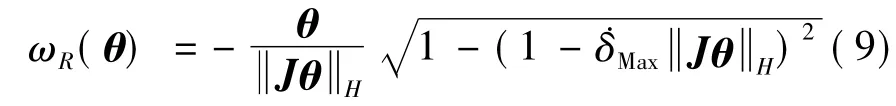
综上，绕特征轴旋转的角速度规划函数为

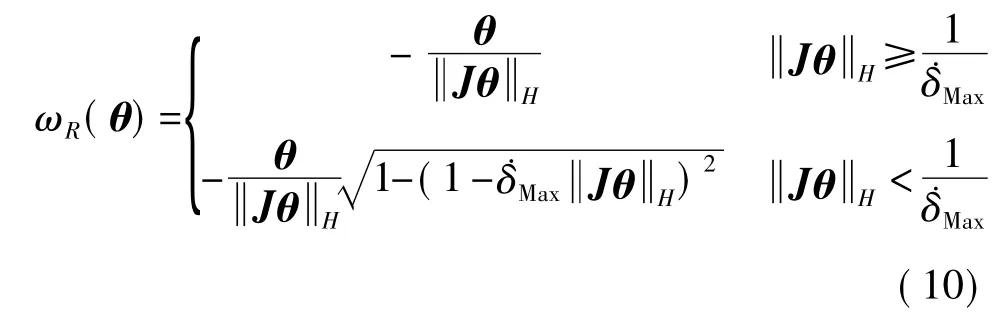
3.2 角动量分配

此节给出角速度规划值与陀螺框架角的映射关系.首先由HR=－JωR得出SGCMGs所需角动量，再按包络性质分配到hxy和hyz上，分配示意图如图3所示.

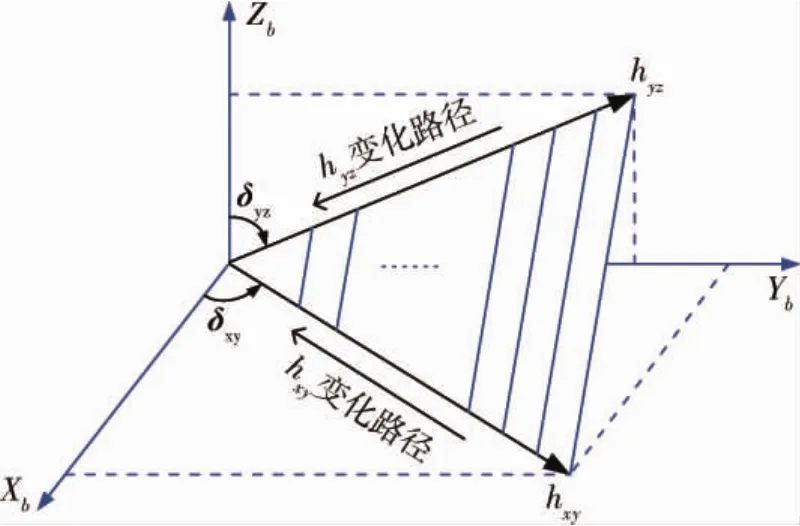
图3 角动量分配示意图Fig.3 Angular momentum distribution

图3中，δxy为hxy与Xb轴夹角，δyz为hyz与Zb轴夹角.hxy和hyz在制动过程中方向不变，全部能力都用于减少角动量，这也体现了特征轴最优时间制动原理.

当HR在包络面上时(加匀速阶段)，hxy和hyz是唯一确定的，设HR=［HxHyHz］T，其分布如第2节所述有两种类型.

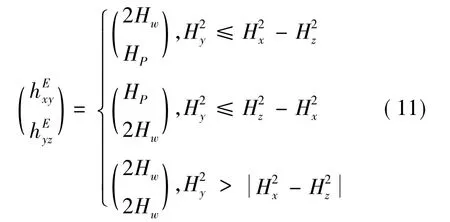
式中，上标E表示包络，HP=为平面包络部分的非饱和分量.

当HR在动量体内部时(减速阶段)，hxy和hyz的分配不再唯一，但基于特征轴最优时间制动则可唯一确定其分配关系，即令hxy和hyz等比例缩短，而比例系数正是HR H.

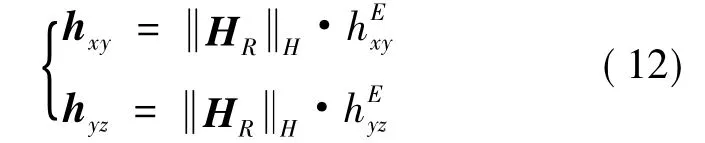
确定平面角动量大小后，其方向δxy、δyz可根据分量关系确定如下:

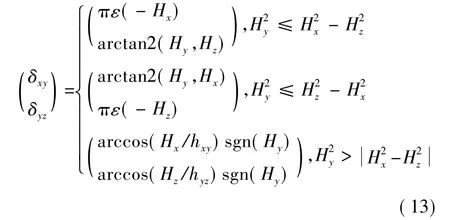
式中，ε(·)为单位阶跃函数，sgn(·)为符号函数.

由hxy和hyz可确定框架角向量:

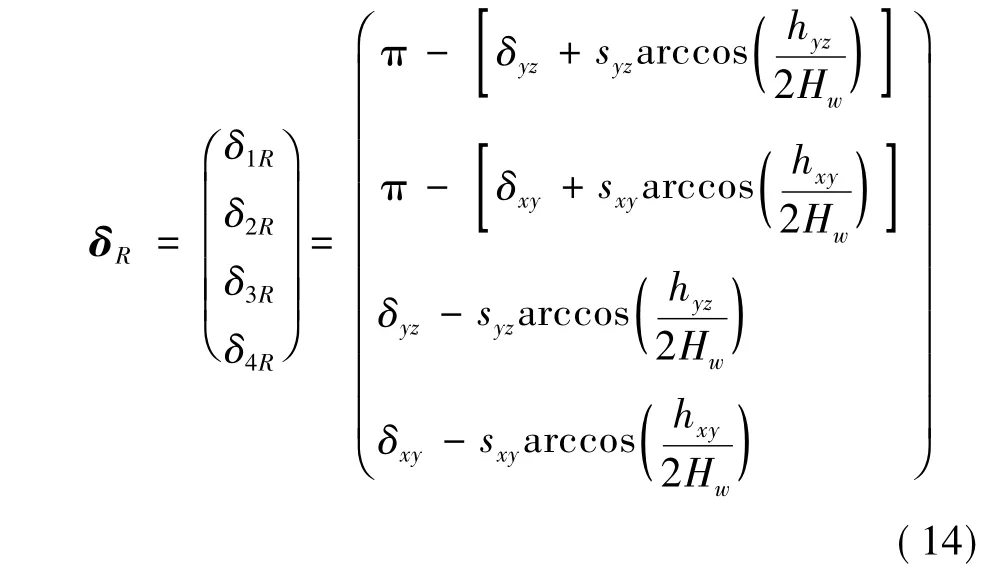
式中sxy，syz=±1，根据陀螺当前位置到下一位置改变最小而定.

3.3 框架角跟踪

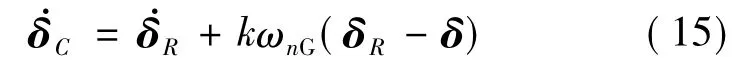
通过角动量分配得到参考框架角向量后，须根据δR确定陀螺框架伺服电机的输入指令，以实现准确跟踪及协调运动的要求.转速指令定义如下:式中，ωnG是正的误差增益;k在框架转速非饱和时为1，饱和时从0到1取值以满足C∞=δMax;δ为当前框架角向量;δR采用向后差分法求解.注意到

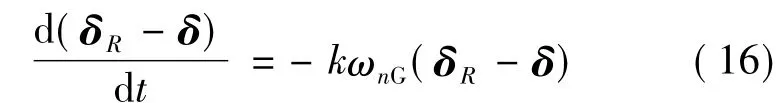
故tlim(δR－δ)=0，即δ对δR的跟踪是渐进稳定的.

3.4 角动量归零

首先确定归零条件.已知制动时间与姿态误差的关系由式(8)表示，而归零时间应与表征系统响应时间的1/ωnG成正比，故有归零条件式

式中，τ为归零控制提前因子.归零条件经监测满足后须启动归零控制，令平面角动量hxy，hyz=0得到参考框架角，框架转速指令依然按3.3节方法计算.

4 混合控制策略

4.1 动量管理

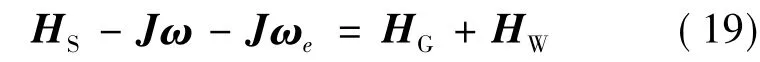
当整星存在角动量偏置时，星体角速度不再满足等式－Jω=HG，此时须使用RWs进行角动量管理，以吸收偏置角动量.积分形式动力学方程为式中，HS为包括执行机构在内的整星角动量，ω为星体相对姿态参考系的角速度，ωe为姿态参考系相对惯性系的角速度，HG、HW分别为陀螺群和飞轮组角动量.不难看出，若施加控制使得HW满足

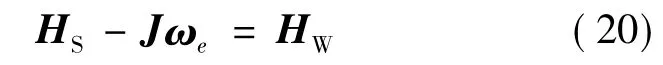
则ω仅由HCMG决定.设飞轮安装矩阵C非奇异，用伪逆解分配飞轮角动量如下:

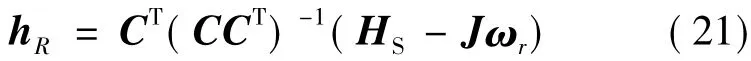
与框架角跟踪类似，取飞轮组角动量跟踪控制律为

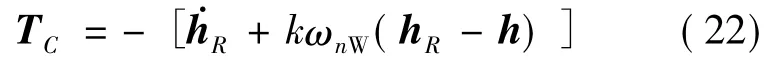
式中，TC为控制力矩，其受限于飞轮额定力矩TLim.TC计算方法与3.3节类似，不再赘述.

4.2 控制切换条件

原则上RWs独立姿控应在SGCMGs角动量归零之后，但实际控制切换不可能等到完全归零后才开始，一是因为陀螺群角动量不可能绝对归零，造成判断条件不现实;二是不利于实现快速稳定，会延误RWs姿控时长，故需设置归零程度系数，最终本文切换条件如下:

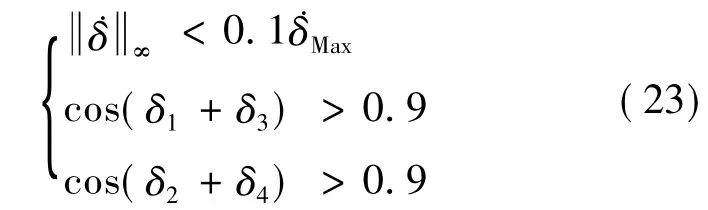
不同归零程度系数决定了RWs独立姿控开始时姿态误差的大小，取10%误差已足够小.

5 SGCMGs单只失效控制策略

5.1 失效构型分析

假设陀螺3失效，其角动量体如图4所示.

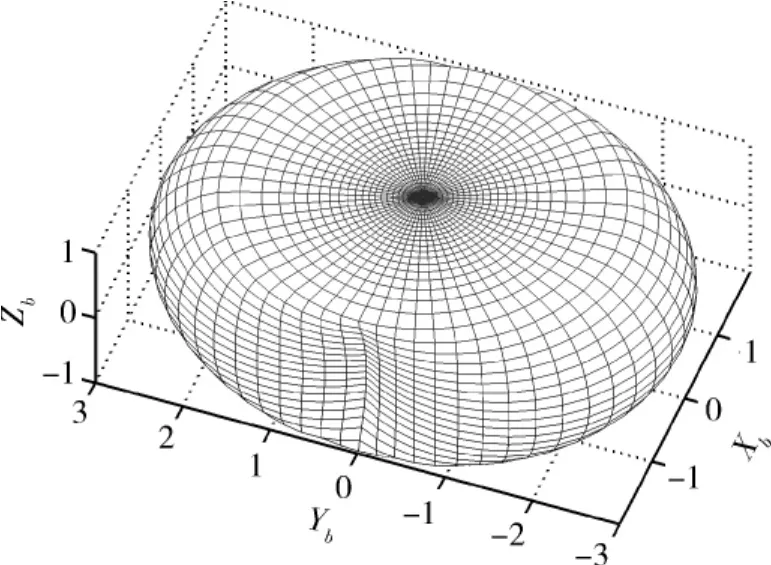
图4 失效构型角动量包络Fig.4 Bounding envelope of single gyro failure

解出uH可得

式中

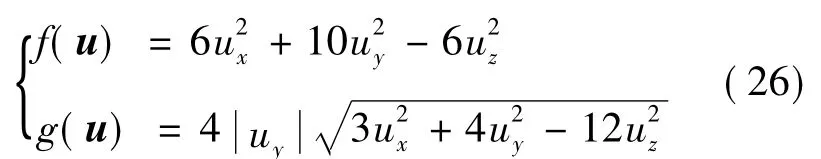
综上，单只陀螺失效的角动量范数表达式为

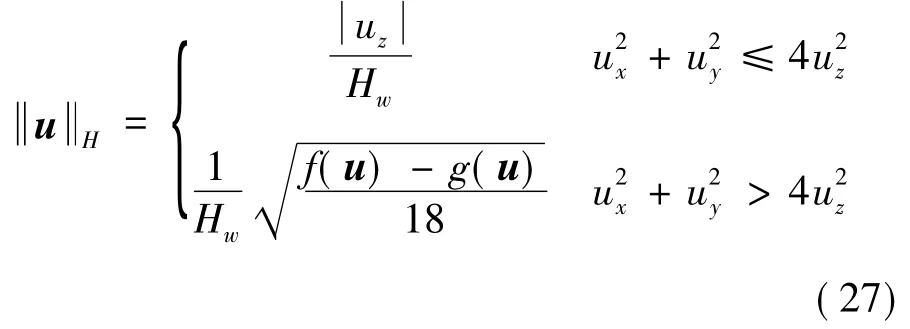
5.2 失效构型角动量分配

3－CMG角动量制动过程中，hxy和hyz端点轨迹为曲线，所以不能以式(12)方法计算，易知hyz大小始终为Hw，而hxy大小按下式计算

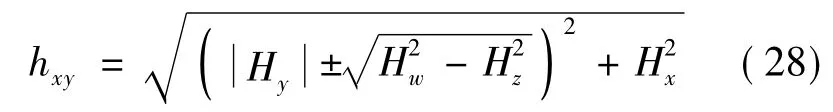
若hxy和hyz在Yb上分量同号则取减，反之取加.

陀螺的具体框架角由下式给出

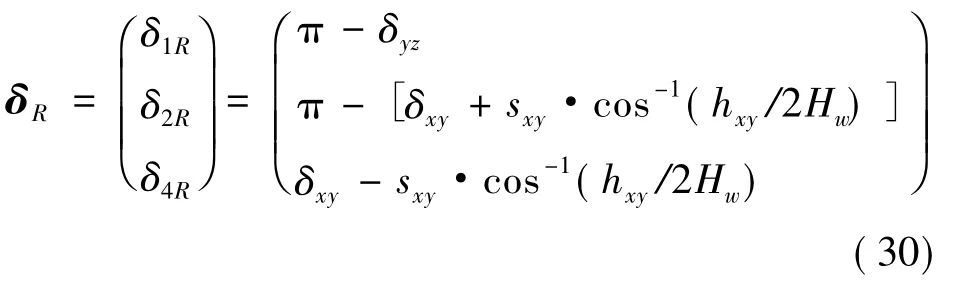
6 仿真校验

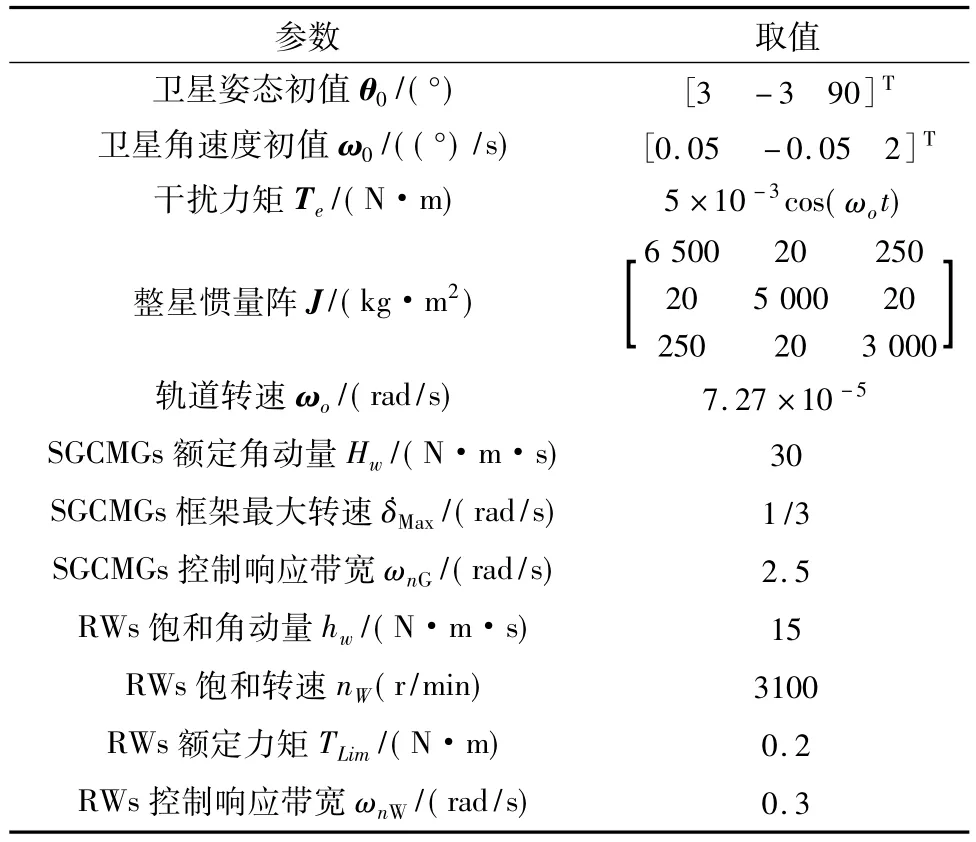
表1 参数设置Tab.1 Parameters setting

4-CMG仿真结果如图5，图5(a)和图5(b)为无角动量偏置情况，图5(c)为加上初始角速度时仿真情况.

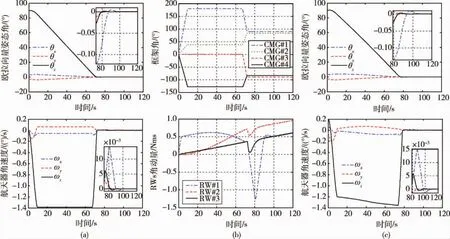
图54-CMG姿态机动Fig.5 Attitude maneuver with 4-CMG

无角动量偏置表示相对惯性系无偏，但相对轨道系有偏置Jx·ωo=6 500×7.27×10－5≈0.5 N·m·s.0～10 s这段时间属于加速阶段，飞轮约5 s内吸收完偏置动量，陀螺框架以最大转速调整到最大角动量构型.10～70 s为匀速和制动阶段，然后SGCMGs角动量归零，转RWs独立姿控，且RWs持续保持偏置吸收.从整个姿控阶段来看，卫星完成绕特征轴90°左右的大角度机动用时约75 s，均速为1.2(°)/s，而绕特征轴最大角速为ωMax=θ0/Jθ0≈1.4(°)/s，表明机动大部分时间卫星都以ωMax旋转.

有初始角速度仿真，前期SGCMGs部分角动量用于抵消偏置，随着偏置逐渐被RWs吸收，卫星角速度也随之逼近ωMax，故整星角动量偏置较大时仅稍微增加机动时间，并不影响姿控策略的正常施行.

失效一个力矩陀螺后，整星相对惯性系无角动量偏置时仿真如图6所示.

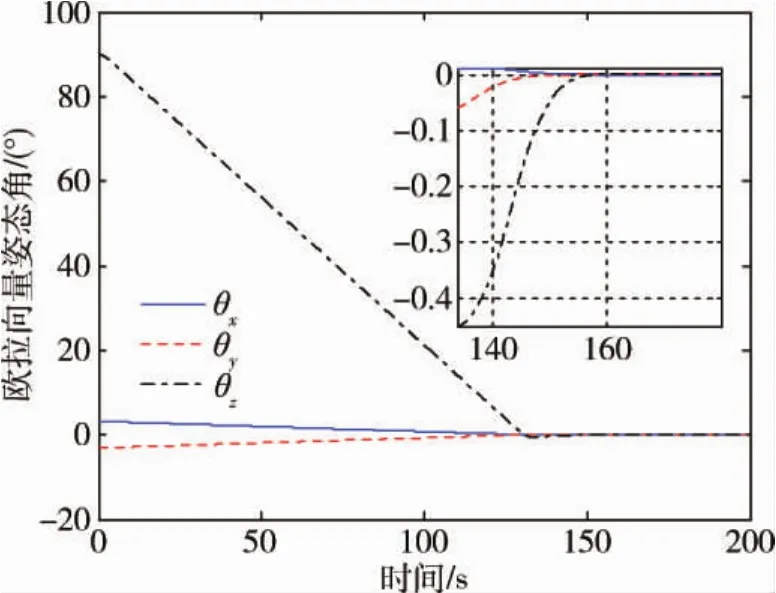
图63-CMG无角动量偏置姿态机动Fig.6 Attitude maneuver based on 3-CMG without bias

从整个控制效果来看，3-CMG依然可以实现此构型下的特征轴最优时间机动，说明失效构型的控制策略依然是有效的.本次SGCMGs控制时长在135s左右，最大角速度约为0.7(°)/s，而失效前控制时间为75s，最大角速度约1.4(°)/s，说明一个陀螺失效后几乎使SGCMGs系统的机动能力降低一半.

7 结论

本文的角动量空间方法整个过程不涉及伪逆求解，故一般不存在操纵奇异.RWs的角动量管理使得SGCMGs角动量与星体角速度成比例关系，从而在角动量域设计控制律成为可能.SGCMGs因其角动量全部用于驱动星体沿最短路径(绕特征轴)旋转故其机动效率逼近全局时间最优.只有双平行等少数解析构型具有其显式表达，如果想在金字塔等其他复杂构型上应用本文算法，需对角动量包络与任意方向向量的关系进行数值拟合.

［1］ BEDROSSIAN N S，PARADISO J，BERGMANN E V，et al.Steering law design for redundant single gimbal control moment gyroscopes［J］.Journal of Guidance，Control，and Dynamic，1990，13(6):1083-1089.

［2］ BROWN D，PECK M A.Scissored-pair control moment gyros:a mechanical constraint saves power［J］.Journal of Guidance，Control，and Dynamic，2008，31(6): 1823-1826.

［3］ WEI B，BAILEY D A，HEIBERG C J.Singularity robust steering logic for redundant single-gimbal control moment gyros［J］.Journal of Guidance Control，and Dynamic，2001，24(5):865-872.

［4］ JIN J，ZHANG J R，LIU Z Z.Error analysis and a new steering law design for spacecraft control system using SGCMGs［J］.Acta Mechanica Sinica，2011，27(5): 803-808.

［5］ 李传江，郭延宁，马广富.单框架控制力矩陀螺的奇异分析及操纵律设计［J］.宇航学报，2010，31 (10):2346-2353.LI C J，GUO Y N，MA G F.Singularity analysis and steering law design for single-gimbal control moment gyroscopes［J］.Journal of Astronautics，2010，31(10): 2346-2353.

［6］ 金磊，徐世杰.采用单框架控制力矩陀螺和动量轮的航天器姿态跟踪控制研究［J］.宇航学报，2008，29(3):916-921.JIN L，XU S J.Attitude tracking control of a spacecraft using single gimbal moment gyros and momentum wheels ［J］.Journal of Astronautics，2008，29(3):916-921.

［7］ 章仁为.卫星轨道姿态动力学与控制［M］.北京:北京航空航天大学出版社，1998:143-145.

［8］ VERBIN D，LAPPAS V J，BEN-ASHER J Z.Time-efficient angular steering laws for rigid satellite［J］.Journal of Guidance，Control，and Dynamics，2011，34 (3):878-892.

［9］ VERBIN D，LAPPAS V J.Rapid rotational maneuvering of rigid satellites with hybrid actuators configuration ［J］.Journal of Guidance，Control，and Dynamics，2013，36(2):532-547.

Attitude Control in Angular Momentum Domain Using SGCMGs

LIANG Jinjin，ZHANG Xiaoke，SONG Xiaozheng，LV Wang
(Shanghai Institute of Satellite Engineering，Shanghai Academy of Spaceflight Technology，Shanghai 201109，China)

A new attitude control method for single gimbal control moment gyros(SGCMGs)that is based on angular momentum domain is presented.In this method，the attitude error is translated to SGCMGs’angular momentum requirement(rather than torque requirement)without having to consider singularities.With double parallel SGCMGs，the SGCMGs are free to perform their eigenaxis time optimal path，when the RWs compensate for the variable unexpected system angular momentum bias.Meanwhile，similar strategy is designed for single gyro failure.Numerical simulations demonstrate that control law in angular momentum domain does not involving singularity，meanwhile with the capability of rapid maneuver and high－level stabilization.

singularities;angular momentum domain;eigenaxis rotation;momentum management

V448.22

A 文章编号:1674-1579(2016)05-0019-06

10.3969/j.issn.1674-1579.2016.05.004

梁金金(1991—)，男，硕士研究生，研究方向为航天器动力学与控制;张小柯(1980—)，男，高级工程师，研究方向为卫星总体设计;宋效正(1980—)，男，高级工程师，研究方向为卫星动力学与控制;吕 旺(1983—)，男，高级工程师，研究方向为卫星动力学与控制.

2016-07-04