一种空间非合作目标的稀疏点云配准算法*
郭瑞科,王 立,吴 云,朱飞虎
(北京控制工程研究,北京100190)
一种空间非合作目标的稀疏点云配准算法*
郭瑞科,王 立,吴 云,朱飞虎
(北京控制工程研究,北京100190)
点云数据配准是三维重构的关键技术之一,为了提高空间非合作目标的稀疏扫描点云数据配准的速度和精度,提出一种改进的基于四点算法的全局配准算法进行初始配准,再使用迭代最近点算法精确配准.针对直接扫描所得到点云数据量大的问题,本文提出一种基于KD-Tree点云均匀采样简化算法,并且对传统基于四点算法中的阈值参数进行了统一,确定了各误差阈值参数和点云密度之间的关系.仿真结果表明,该方法能够快速、有效地实现卫星稀疏点云的配准,改进的四点算法配准耗时仅为几何哈希算法的42.49%.
稀疏点云;点云配准;四点算法;ICP算法
0 引言
空间非合作目标的在轨服务技术可实现对目标航天器的在轨维护,空间垃圾碎片清理、抓捕或破坏敌方军事卫星等,具有很高的民用和军事价值.在这些在轨服务任务中,服务航天器在跟踪、接近和抓捕目标时,需要实现航天器和目标间的相对位置和姿态测量.相比较于传统的合作目标,非合作目标上没有光标线或者角反射器等配合标志,无法提供显著、可靠的参考信息,这就给非合作航天器的准确位姿测量带来了极大的挑战.特别是对于完全未知的空间目标,需要首先在轨建立三维模型,然后利用所重构的三维模型实现六自由度位姿估计和特征识别.因而如何对未知目标进行三维重构,成为了非合作目标在轨服务的一项关键技术.
激光扫描敏感器通过获取目标表面的点云数据,得到目标三维模型,具有精度高、不受光照影响的优点.由于敏感器视场角的限制,要得到目标完整的三维模型,需要从多个视角对目标进行扫描,将不同视角得到的点云数据配准到同一坐标系下.点云配准一般包括全局配准和精确配准两个步骤,全局配准缩小两片点云之间的旋转和平移错位,为精确配准提供比较好的初值.
常用的精确配准算法是Besl和McKay于1991年提出的点到点的ICP算法,可以在比较好初值的情况下实现点云的精确配准[1].
针对任意初始位置点云数据的全局配准问题,学者们做了大量研究.Wolfson等[2]提出了几何哈希算法,用于点云数据的全局配准.作为改进,吴君恺等[3]提出了一种多边形哈希表的配准算法,将点对之间的距离存储在哈希表中,在较低时间复杂度下实现点云数据的自动全局粗配准,但是所需要的内存空间比较大,不适合空间应用.Rusu等[4]提出的FPFH(fast point feature histograms)基于局部几何特征的全局配准方法,计算速度快,但是依赖点云的邻域特征,不适合稀疏点云.谢冬香等[5]采用主元分析法,可较快配准两幅点云,但要求两片点云重叠区域足够大,且二者的主轴形状相差不大.
对于两幅三维点云的配准,至少需要从各自点云中选取对应不共线的三点,才能计算出二者的刚体变换矩阵.若待配准两片点云P、Q分别有m、n个点,在P、Q中选取对应的三点计算旋转平移矩阵,时间复杂度可达 O(m3n3).Irani等[6]采用基于RANSAC(random sample consensus)的方法配准,可以降低复杂度到O(n3logn),然而对于空间应用,时间复杂度还是太高.考虑在P点云中选取更多的共面点(5个或者以上),则在Q点云中能成功选择到正确的对应点集的概率急剧降低,难以实现配准[7].
四点算法是Aiger等人于2008年提出的一种基于RANSAC法则的全局配准算法,通过在点集中选取共面四点,可实现三维点云数据的配准,时间复杂度只有O(n2),并且受噪声影响小[8].但是算法中涉及到的可调阈值参数较多,当配准对象变化或者多幅点云连续配准时,影响配准的效率,仍有改进的空间.
本文针对空间目标需要内存占用小,点云稀疏的特点,采用基于改进四点算法的全局配准算法,具有对噪声鲁棒性好,速度快的优点,可以得到满足精度的初始配准结果.将全局配准的结果作为精确配准算法ICP的初值,可以保证收敛精度的同时,提高配准的效率.仿真实验验证,该方法可以很好的实现卫星稀疏点云数据的配准.
1 点云数据的简化
激光扫描敏感器的测量精度高,尤其是在近距离扫描时,采用高效的李萨茹扫描方式和图1所示,获取的单幅扫描数据点数多达数万到数十万.这样大的数据量对于星载计算机有限的存储空间和计算能力带来了比较大的挑战.图1可知边缘点云密度高于中间部分,而且点云都集中在扫描线上,因而并不是所有的点都可用于配准.其中冗余的点云数据如果都参与配准,不仅会降低计算速度,而且点越多,越难从中找到符合特征的点对,影响配准的精度.
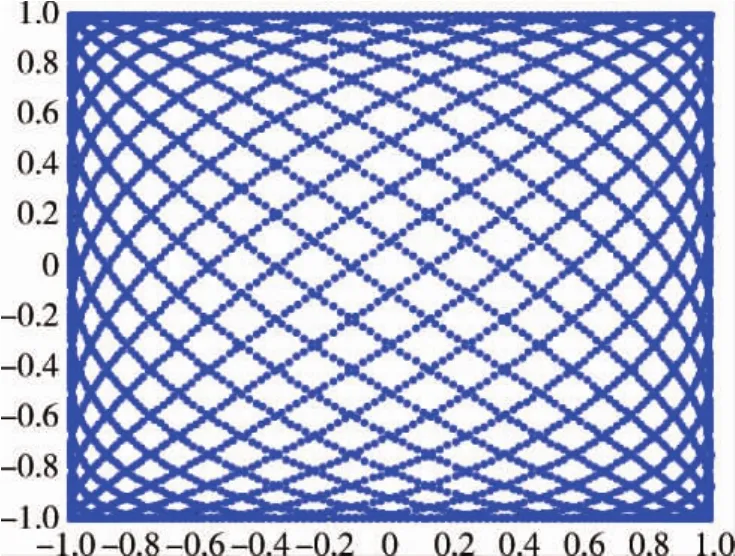
图1 李萨茹扫描方式Fig.1 Lissajous scan pattern
为了解决上述问题,必须对测量的点云数据进行精简,以提高计算速度,减少存储空间,提高配准精度等.考虑到我们所处理的对象为卫星点云,在空间模型重建中对时效性要求较高,本文提出一种基于KD-Tree点云均匀采样算法对点云数据进行精简.
KD-Tree是三维点云数据中常用的一种数据格式,可以快速实现数据点的k邻域搜索[9],也就是在点集中找到k个与该点欧氏距离最近的点.
在基于KD-Tree点云均匀采样算法中,首先利用KD-Tree对待简化点云数据建立空间拓扑结构,搜索点集中每个点的k邻域,然后计算该点与k个最近邻点的重心,用该重心代替这点,最后对所得到的点集均匀采样,可以得到简化的稀疏点云.
图2是从一个视角扫描得到的单幅原始卫星模型点云,包含10171个数据点,采用上述简化算法,k 取4,均匀采样率设置为7%.得到简化后的点云如图3所示,数据点数为710,可以看到数据得到很好的精简,卫星模型的特征也可以比较好的保留.

图2 原始点云Fig.2 Original point cloud
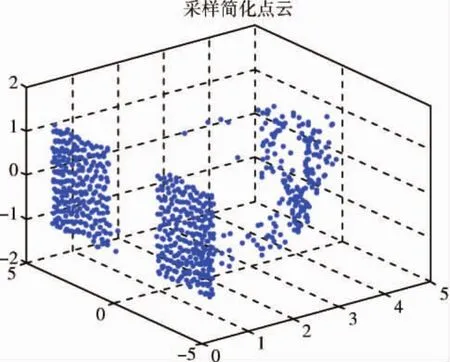
图3 简化后的点云Fig.3 Simplified point cloud
2 基于改进四点算法的全局配准算法
本文针对原始四点算法中阈值参数比较多的情况,通过点云密度对阈值参数进行了统一,简化了多视角点云配准时的阈值参数设置.
2.1 四点算法
四点算法在每次的迭代中,在点集P(data点集)中随机寻找不在同一条直线上的共面四点,根据共面四点的两条对角线交点将线段所分比例r1、r2在刚体变换中的不变性,在点集Q(model点集)中选取对应的共面四点所图5所示,这两对共面四点组成一致共面四点集,利用该一致共面四点集可以计算出旋转矩阵R和平移矩阵T.四点算法不需要计算复杂的几何特征,速度快,对噪声具有比较高的鲁棒性.
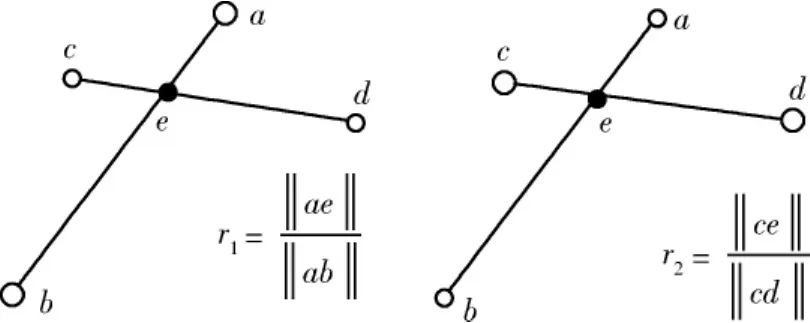
图4 中所选的共面四点[8]Fig.4 Four coplanar points extracted from
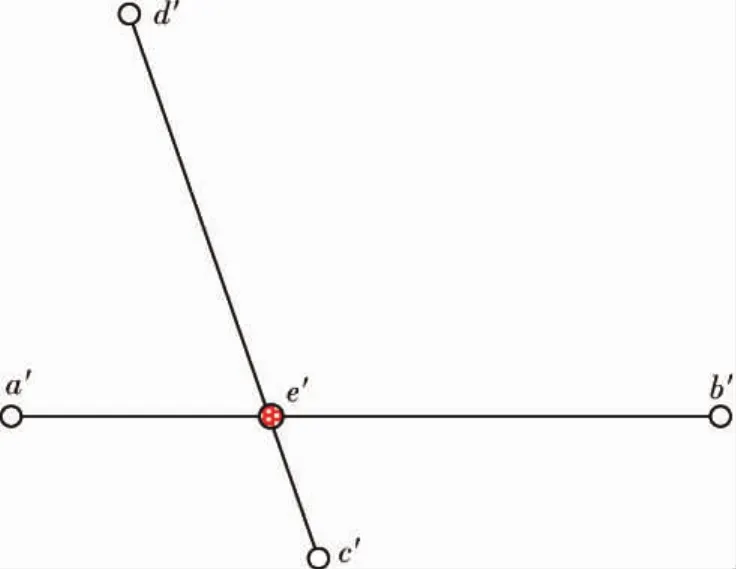
图5 Q中对应的共面一致四点Fig.5 Four affine invariant congruent points extracted from Q
四点算法中,Q点集中候选点对可以用式(1)中共面四点长度来筛选,即满足与线段ab和cd近似相等的点对都是对应候选点对,δ1为该长度的误差阈值;根据不变量r1、r2由式(2)可以确定可能的交点e';近似相等交点所对应的点对即组成Q点集中的共面一致四点.利用点集(a,b,c,d)和(a',b',c',d')可以计算对应的欧式变换矩阵,用所得到的欧式变换矩阵作用于点集P,验证在一定阈值下,P点集中成功配准到Q点集的点数目,即一致性度量.
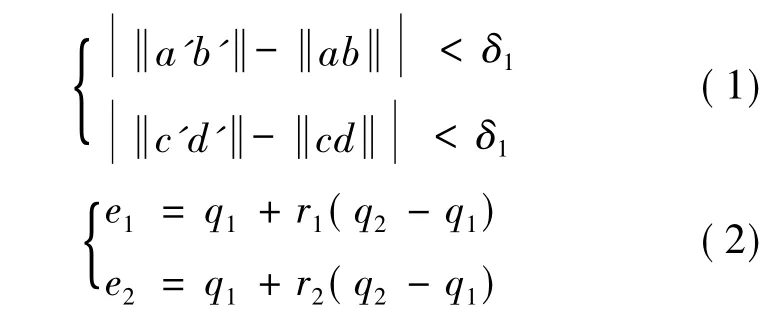
式中,q1、q2是从点集找到的长度符合的候选共面四点集,q1是候选的a'b'点,q2是候选的c'd'点.
2.2 四点算法的阈值参数设置方法
文中所配准的点云数据是从完全非合作目标扫描所得到的,全局配准中没有点云数据的先验知识,同时四点算法中涉及到的误差阈值参数众多,这对算法中的阈值参数设置带来了挑战.在轨模型重建中需要多次点云配准,每次配准的两幅点云特征都有所差别,如果分别设定这些阈值参数,可能会费时费力,甚至会导致不能成功配准.
点云数据密度是稀疏点云的关键几何特征,本文中待配准点云的密度τ,定义为点云中所有点k邻域距离的平均值.一般三维散乱点云的k邻域点数可设置为6,即前后左右上下六个方向,这样可以比较好的保持点云的三维特征,准确确定其它局部几何特征.本文中待配准的点云是经过简化的卫星点云,卫星帆板和本体部分以平面特征为主,因而k邻域点数设置为4,能比较好的保留卫星点云特征,准确估计点云数据密度.本文通过确定点云密度与各误差阈值参数的关系,对误差阈值参数进行了统一.
上述四点算法中涉及到的参数有:在Q点集中筛选候选对应点对时的距离误差阈值δ1;选取近似相等交点时的位置误差阈值,即满足 e1-<δ2可认为二者相等;一致性度量时,若欧氏变换后P点集与Q点集中点对的距离小于误差阈值δ3时,标记为配准成功的点对.
本文通过仿真实验确定了各误差阈值δi与点云密度τ之间的关系,这样当多幅点云数据连续配准时,无需重新调节阈值参数,有效提高了配准算法的稳定性和自动化程度.
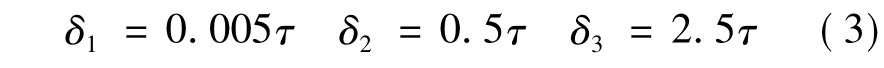
3 基于ICP算法的精确配准算法
ICP算法是在两个点集中搜索最近的点对,以这些最近点对作为控制点来估算旋转变换矩阵和平移变换矩阵,并将这个坐标变换作用到data点集上,迭代地进行这一操作过程,直到某个表示正确匹配的收敛准则得到满足.
由于待配准的两幅点云只有部分区域是重合的,在搜索最近点对的时候,不可避免的会存在错误的匹配点对.为了消除这些错误匹配点对对精确配准结果的影响,需要剔除这些错误匹配点对.点云数据密度是稀疏点云的关键几何特征,初始配准时已经估计过点云的密度.对于部分重叠的两片点云,只有使用重叠区域的最近点对,才能准确计算出两者之间的变换矩阵,而非重叠区域的最近点对距离偏大.本文采取距离阈值的方法来剔除错误匹配点对,即认为搜索的最近点距离大于点云密度一定倍数的点对为错误匹配点对.
多幅点云配准的基础是两幅点云的配准,配准后的两幅点云需要去除掉重叠区域冗余的点云,才能得到两个视角拼接到一起的单幅完整点云,方便用于后续视角的配准拼接.由ICP配准算法的原理可知,配准中最后一次迭代时所搜索到的最近点对,就是两幅点云的重叠区域,对重叠区域的每对点云取坐标的平均值,将平均值作为该区域的新数据,即可实现重叠区域冗余点云的去除.
4 实验仿真
本文仿真实验使用简化后某卫星仿真点云数据,model点云为0°视角卫星点云数据,data点云是30°视角点云数据,数据点数为719,两幅点云有部分重叠.配准误差定义为均方根误差(root mean square error,RMSE)
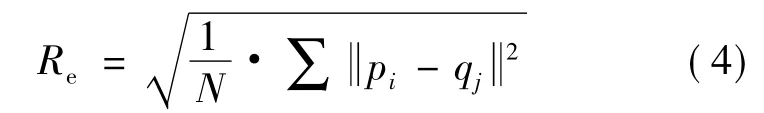
式中,N为欧氏变换后两块待配准点云重叠部分点数目,pi、qj分别为欧氏变换后点云中重叠区域的点.
首先使用基于改进四点算法的全局配准算法进行了配准.图6是待配准的两片点云,圆点为model点云,五角星为data点云.图7是全局配准的结果,可以看到对于两幅初始位置偏差比较远的稀疏点云,全局配准算法能够比较好的实现配准,配准误差为0.1339.从图9所示的全局配准点云在OYZ平面上的投影,可以看到沿X轴方向仍有滚转的误差,需要精确配准算法的进一步优化.
精确配准使用全局配准点云的结果作为初始值,配准过程中通过距离阈值去除掉错误匹配.图8是精确配准后的点云,可以看到两个视角的点云已经很好的配准到一起,配准误差降低到0.0908.图10是精确配准的点云在OYZ平面的投影,相比于图9,滚转误差已经消除.从图11的误差曲线可以看到迭代15次时,已经收敛.
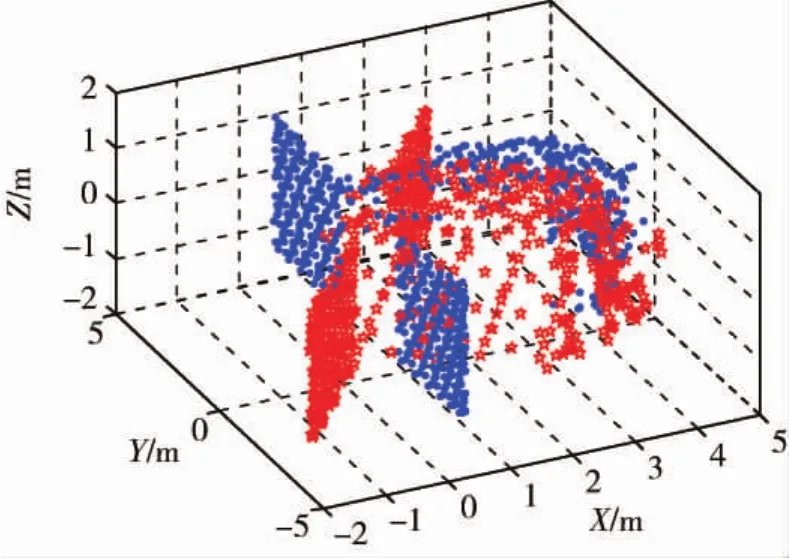
图6 待配准点云Fig.6 Model and Data point cloud
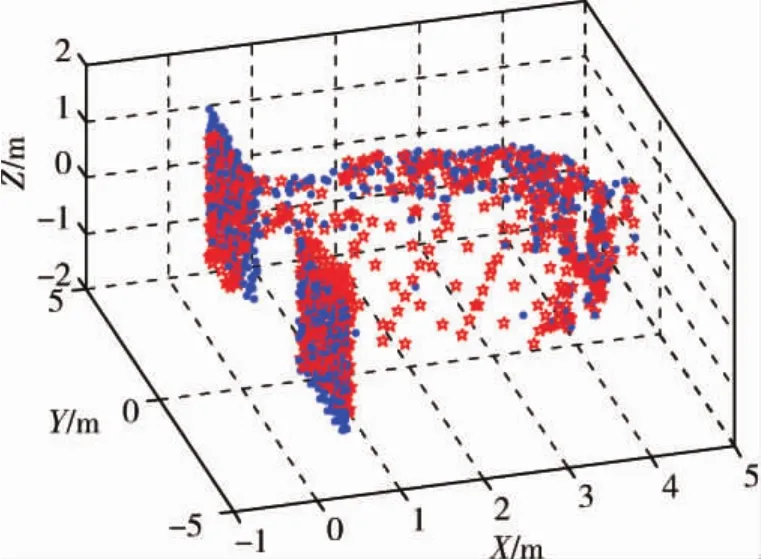
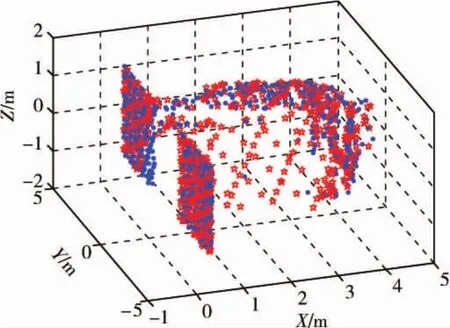
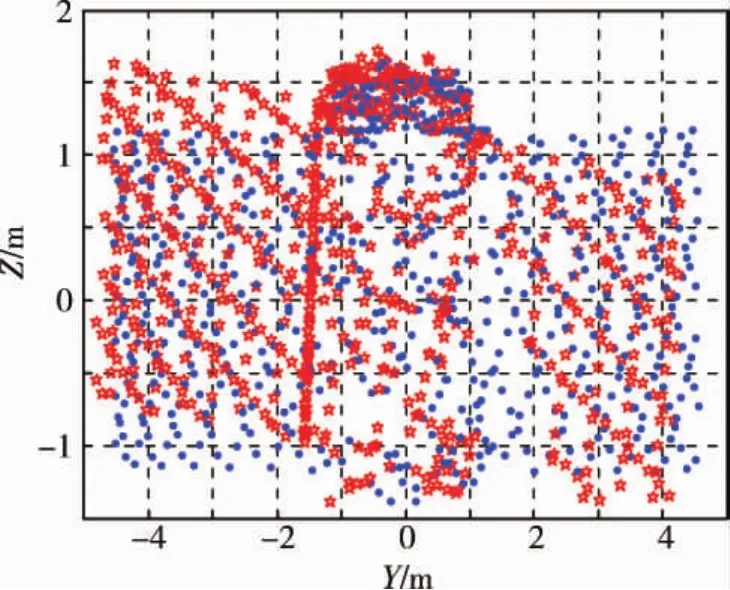
图9 全局配准点云在OYZ平面投影Fig.9 Projection of coarse registration in OYZ
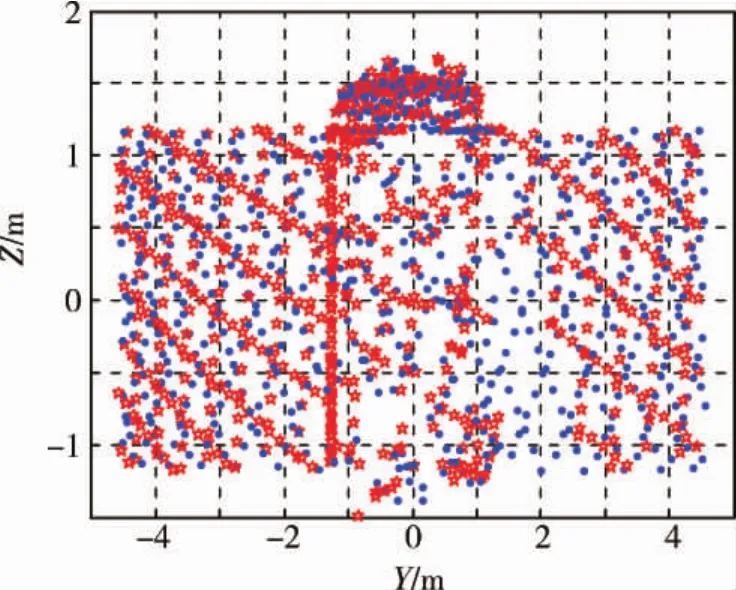
图10 精确配准点云在OYZ平面投影Fig.10 Projection of fine registration in OYZ
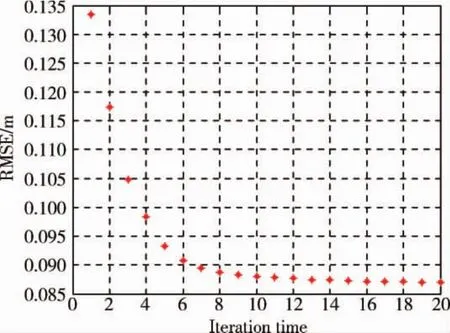
图11 均方差变化曲线Fig.11 Variation of RMSE
图12所示是去除掉重合部分冗余点云,所得到的拼接在一起的两个视角的点云.圆点是两个视角的重叠部分,五角星是仅在data点集中的点云,十字是仅在model中的点云.
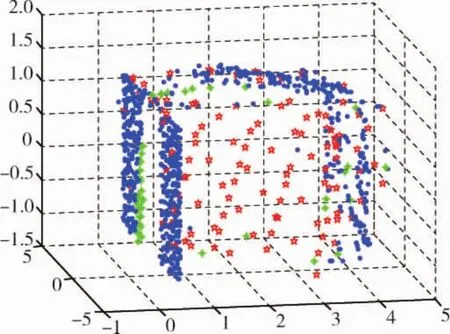
图12 拼接在一起的两幅点云Fig.12 Spliced point cloud
传统的几何哈希算法需要先离线建立哈希表,再搜索配准,从表1可以看到,文中的全局配准算法用时小于几何哈希算法配准,配准速度得到提高,二者精度相差不大.
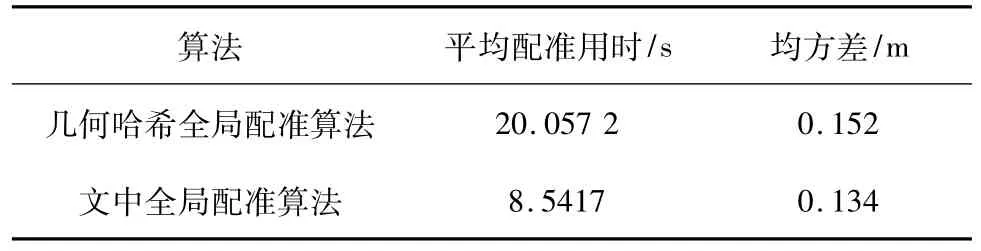
表1 文中配准算法与几何哈希配准算法对比Tab.1 The comparison with Geometric Hashing
5 结论
两幅点云的配准是多幅点云配准的基础和关键,空间应用中,点云的配准算法要兼顾精确性、快速性和内存占用大小等因素.本文针对卫星扫描点云数据,提出基于KD-Tree点云均匀采样简化算法,在保持卫星特征的情况下比较好的实现点云简化.对于卫星稀疏点云数据,使用基于改进四点算法进行初始配准,将初始配准结果作为精确ICP配准的初值,实现了点云数据的精确配准.对于四点算法中误差阈值参数多的情况,给出了误差阈值参数与点云数据密度之间的关系,有效提高算法的稳定性.作为多幅点云的配准基础,研究了两幅点云配准之后重叠区域的去除,以方便未来实现多幅点云的配准.
[1] FISHLER M A,BOLLES R C.Random sample consensus:a paradigm for model fitting with applications to image analysis and automated cartography[J].Communications of the ACM.1981,24(6):381-395.
[2] WOLFSON H,RIGOUTSOS I.Geometric Hashing:an Overview[J].IEEE Computer Science and Engineering,1997:10-21.
[3] 吴君恺,杨光.基于点云配准的空间目标定位技术的补偿问题研究[C]//全国射线数字成像与CT新技术研讨会,厦门,2014:20-28.WU J K,YANG G.Compensation in space targeting technology based on point cloud registration[C]//The X-ray Digital Imaging and CT New Technology Conference,Xiamen,2014:20-28.
[4] RUSU R B.Fast Point Feature Histograms(FPFH)for 3D Registration[C]//In Robotics and Automation,2009.ICRA 09.IEEE International Conference.New York:IEEE,2009:3212-3217.
[5] 谢冬香,刘先勇.一种快速的三维点云自动配准方法[J].微型机与应用,2013,32(6):47-49.XIE D X,LIU X Y.A robust and automatic registration of 3D point sets[J].Microcomputer&its Applications,2013,32(6):47-49.
[6] IRANI S,RAGHAVAN P.Combinatorial and experimental results for randomized point matching algorithms [J].Computational Geometry,1999,12(1-2):17-31.
[7] YAO L,RUGGERI M R,TADDEI P,et al.Robust surface registration using N-points approximate congruent sets[J].EURASIP Journal on Advances in Signal Processing,2011:72.
[8] AIGER D,NILOY M J.4-Points Congruent Sets for Robust Pairwise Surface Registration[J]ACM Transactions on Graphics(TOG),2008,27(3):85-94.
[9] BENTLEY J L.Multidimensional binary search trees used for associative searching[J].Communications of the ACM,1975,18(9):509-517.
A Sparse Point Cloud Registration Algorithm of Non-Cooperative Spacecraft
GUO Ruike,WANG Li,WU Yun,ZHU Feihu
(Beijing Institute of Control Engineering,Beijing 100190)
The point cloud data registration is one of the key technologies of three-dimensional reconstruction.To solve the registration issue of sparse point cloud scanned from the non-cooperative spacecraft,we propose a improved 4-points congruent sets(4PCS)algorithm to obtain the preliminary registration result,and optimize the final alignment with the improved iterated closest points(ICP)algorithm.Then,a novel point cloud simplification algorithm using uniform sampling is proposed based on KD-Tree.The uniform relation of the threshold parameters is established via the density of the point cloud.The results show that the proposed algorithm can effectively achieve good alignments of the sparse point cloud of the satellite,and the consuming time is decreased to 42.49%compared with the Geometric Hashing algorithm.
non-cooperative target;sparse point cloud;point cloud registration;4PCS algorithm;ICP algorithm
TP391
A 文章编号:1674-1579(2016)05-0031-06
10.3969/j.issn.1674-1579.2016.05.006
郭瑞科(1989—),男,硕士研究生,研究方向为模式识别与智能系统;王 立(1977—),男,研究员,研究方向为视觉导航;吴 云(1985—),男,工程师,研究方向为激光雷达;朱飞虎(1985—),男,高级工程师,研究方向为激光雷达.
*国家重点基础研究发展计划(973)资助项目(2013CB733100).
2016-04-06

