城市轨道交通火灾疏散预动作时间计算
林 铭, 徐汇川, 金 华
(中国人民公安大学 警务信息工程学院, 北京 102600)
城市轨道交通火灾疏散预动作时间计算
林铭, 徐汇川, 金华
(中国人民公安大学 警务信息工程学院, 北京102600)
摘要:针对国内外城市轨道交通火灾事故频发的现状,对城市轨道交通火灾疏散预动作时间与乘客人群密度之间的关系进行研究.使用Anylogic软件进行Agent建模,将乘客分为两类,彼此之间进行灾情信息交流.在仿真实验中改变人群密度大小,观察预动作时间的不同.结果表明,在人群密度为0.08~1.04人/m2时,预动作时间变化较小;而在人群密度为1.04~2.40人/m2时,预动作时间增大.
关键词:城市轨道交通; 预动作时间; 人群密度; 火灾; 疏散
近年来,城市轨道交通发展迅速,北京的城市轨道交通在2013年的日均客流量就已经突破千万人次.面对如此庞大的客流量,城市轨道交通运营工作的重点之一就是要保障乘客的人身安全,避免由突发事件造成的不良后果.城市轨道交通运营过程中常见的突发事件一般可以分为三类:运营生产类、公共安全类、自然灾害类[1].在公共安全类突发事件中,火灾事故是发生频率高、危害大、后果严重的事故.从20世纪80年代至今,国际上发生的有严重影响后果的城市轨道交通火灾事故至少有13起以上[2].同时,由于城市轨道交通往往采取地下或高架形式,具有封闭性强、运行速度高、起停频繁、客流量大且来源复杂、乘客自助乘车、应急疏散难度大等固有特点,火灾一旦发生,不仅会造成设备设施的损坏,更会造成乘客伤亡的严重事件[3].因此,本文对城市轨道交通中火灾疏散的预动作时间进行了研究,为火灾疏散提供有益的参考.
1疏散时间组成
目前,美国国家标准技术研究所建筑与火灾研究室提出的ASET(Available Safe Egress Time)和RSET(Required Safe Egress Time)是衡量人群在面对火灾事故能否安全疏散的一个重要时间标准.其中ASET是可用安全疏散时间,RSET是必须安全疏散时间,如果必须安全疏散时间小于可用安全疏散时间时,即可判断人群能够进行安全疏散,反之,则不能.必须安全疏散时间与可用安全疏散时间的关系如图1所示.
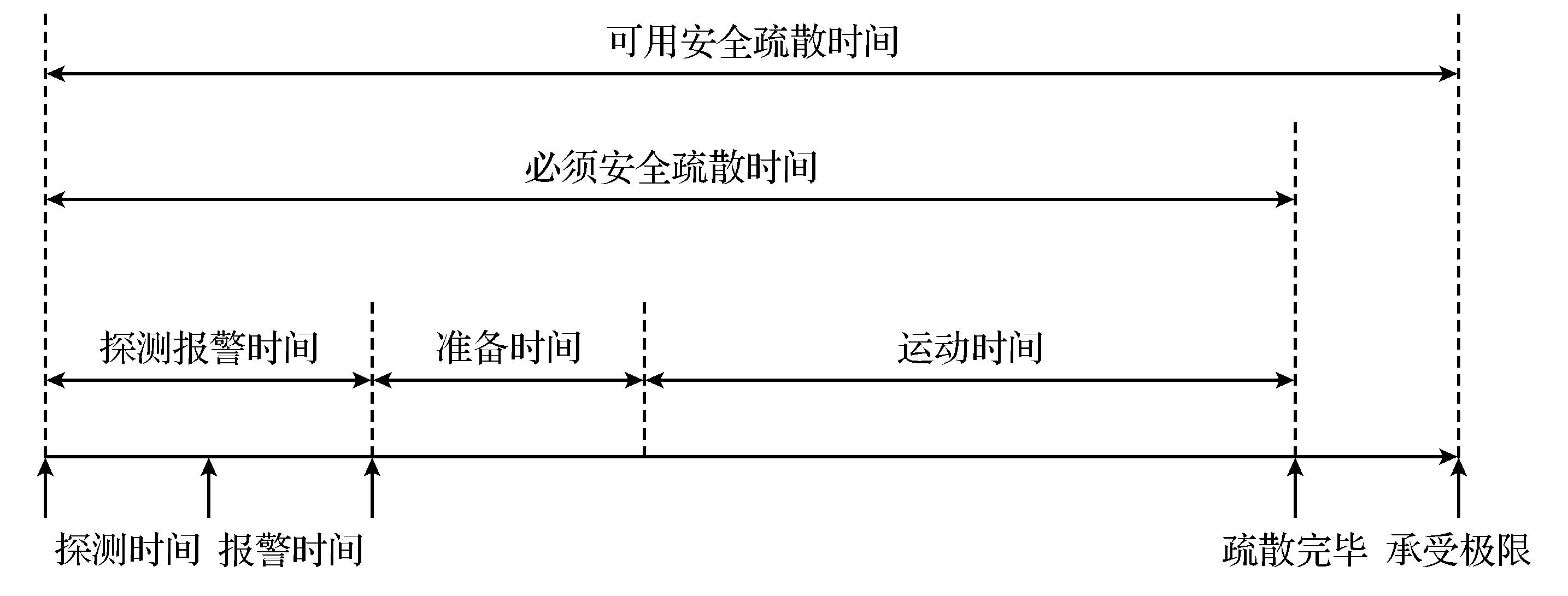
图1 必须安全疏散时间与可用安全疏散时间的关系
从图1可以看出,必须安全疏散时间由三部分组成, 即探测报警时间、准备时间、运动时间[4]. 探测报警时间是城市轨道交通站点发现火灾事故并用相应的广播设施或工作人员对灾情进行传播,引导疏散所花费的时间. 准备时间表示人群从发现险情到开始疏散所经历的时间, 也就是本文所要研究的预动作时间. 运动时间是全部人员疏散完毕所经历的时间. 这三个阶段是城市轨道交通发生火灾事故时,乘客需要经历的疏散过程,三者总和为“必须安全疏散时间”. 可用安全疏散时间是城市轨道交通站点建筑能承受的极限疏散时间,“必须安全疏散时间”应小于“可用安全疏散时间”. 人们对探测报警时间和运动时间的研究相对较多[5-6],但是对预动作时间的研究较少.这是因为预动作时间涉及到人群中的信息传递, 人群的心理活动、人群的密集程度等众多难以衡量的因素, 很难找到合适的方法对预动作时间进行计算和准确的表达. 并且由于预动作时间通常较短, 在实际应用时往往被人们忽略. 但是在人群高度密集、建筑结构封闭、疏散要求高的城市轨道交通站点中, 不能忽略这一预动作时间, 而需要对必须安全疏散时间进行较为准确的估算, 以便满足疏散要求.本文采用agent建模方法,对不同人群密度下的预动作时间进行研究,分析城市轨道交通不同人群密度对应的火灾疏散预动作时间, 为城市轨道交通中的火灾疏散提供有益的参考.
2实验
2.1模型和仿真工具选择
选择agent模型对人群的预动作时间进行研究.Agent是一种与现实人类行为较为接近,可以在计算机上运行的实体.其包含了知识、信念、承诺等现实人类才具备的能力,因此适用于对人类行为进行仿真,模拟人群之间的信息交互、心理传播以及某些复杂的群体行为[7].
仿真工具使用俄罗斯XJ Technologies公司的复杂系统仿真软件AnyLogic.基于AnyLogic环境可实现agent建模,而且良好的可视化界面使得建模过程变得更加直观快捷[8].本文对城市轨道交通中火灾疏散时预动作时间的研究使用AnyLogic中的agent建模部分.
2.2参数确定和模型建立
本文研究的是局部聚集人数大于等于50人的场所.因为当公共场所聚集人数少于50人的时候,人群分布较为分散,信息在人群中传递没有连续性,对于预动作时间的影响主要在于个人的差异性,与聚集人群的数量关系不大[9].以深圳城市轨道交通站点老街站为例,站厅面积为625 m2,一般高峰期时站厅人数可达到1 500人,人群密度为2.4人/m2.因此,本文研究人群密度为0.08~2.4人/m2时,人群疏散的预动作时间.
使用Anylogic进行agent建模,首先需要构造一种agent类,在agent类里对乘客的行为进行设定.将agent模型分为两类,一类是没有意识到发生火灾的乘客,命名为“无意识的乘客”;另一类是意识到发生火灾的乘客,命名为“有意识的乘客”.在火灾发生初期,通过城市轨道交通的警报广播,少部分“无意识的乘客”迅速转变为“有意识的乘客”.然后,“有意识的乘客”随机向周围的乘客传播发生火灾的信息,逐步所有的“无意识的乘客”都将转变为“有意识的乘客”,这一过程总共需要的时间就是预动作时间.具体状态变迁图如图2所示.
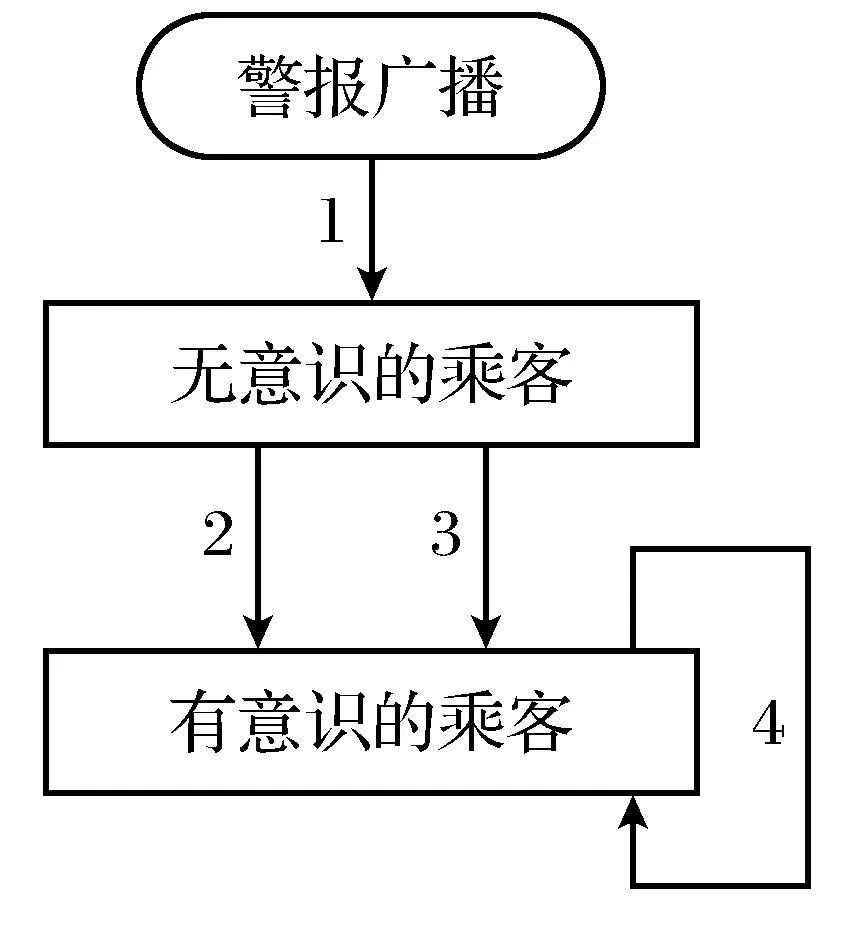
图2 乘客状态变迁图
两个矩形框分别代表了两种不同的agent类,即“无意识的乘客”和“有意识的乘客”.其中“无意识的乘客”可以转变为“有意识的乘客”,但“有意识的乘客”无法转变为“无意识的乘客”,这符合现实中的一般情况.当城市轨道交通站中发生火灾,探测器探测到火灾信号后,通过警报和广播通知乘客,即图中的过程1.部分无意识乘客接收到警报和广播信息后,开始向有意识乘客转变,即图中过程2.根据汪金辉[10]等人的研究结果,我们将最初的“无意识的乘客”转变为“有意识的乘客”的概率设置为0.03,即跃迁概率为0.03.当部分“无意识乘客”转变为“有意识的乘客”后,开始随机对周围人群发布火灾信息,呼吁周围的人群快速撤离.使用Java语言send To Random Connected(“run”)命令控制.此时 “无意识的乘客”接收到“有意识的乘客”发出的“run”的消息以后,得知火灾事故发生,立即转变为“有意识的乘客”,即过程3.同时,“有意识的乘客”也会随机对其周围的有意识人群发出逃跑信号,即过程4.
3仿真实现与结果分析
3.1仿真实现
对人群密度为1.6人/m2情况下进行火灾预动进行仿真,结果如图3所示.图3为乘客数量转变与时间关系图,横轴代表时间,纵轴代表“有意识的乘客”数量.从图3可以看出在火灾事故发生初期,较少的乘客对火灾事故是意识的,随着时间的增加,越来越多的乘客开始变成“有意识的乘客”,即曲线的增速在初期是相对较快的;随着时间的推移,有意识乘客人数的增加速度开始减缓,当有意识乘客人数超过800人后,曲线趋于饱和,即代表全部乘客都转变为“有意识的乘客”.此刻的时间数值,就是该文所要研究的在特定人数下的预动作时间,即全部乘客转变为“有意识的乘客”所用时间.
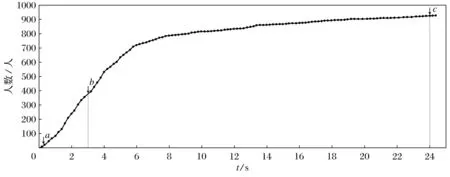
图3 有意识的乘客数量与预动作时间关系图

图4 1.6人/m2下预动作过程仿真结果
根据图3中的对应关系,我们在时间横轴上截取了3个时间点进行研究,为0.2 s、3 s、24 s,对应预动作开始、中期和后期,分别用(a)、(b)、(c)来标注.这三个时间点所对应的仿真结果如图4所示,展示了仿真实验初期、中期以及后期的乘客转变情况.在火灾还未发生的时候,这些乘客都属于“无意识的乘客”.随着火灾事故的发生,警报广播开始通知灾情,少部分反应迅速的乘客开始意识到危险的存在,由“无意识的乘客”转变为“有意识的乘客”.图4(a)为火灾初期模拟仿真结果,可见图中大部分都是小圆圈,极小部分是黑色圆点,这表明了在火灾事故发生初期,大部分乘客都处于“无意识的乘客”的状态,只有少数反应迅速的乘客在听到警报广播后转变为“有意识的乘客”.图4(b)为3 s后的模拟仿真结果,越来越多的小圆圈转变为黑色圆点,这表明了随着火灾事故的演变,越来越多的乘客转变为“有意识的乘客”.图4(c)为24 s后的模拟仿真结果,绝大部分小圆圈都转变为黑色圆点,这表明了在随着火灾事故发展到一定阶段,乘客通过警报广播和自身信息传递的作用,大部分都转变为“有意识的乘客”.
3.2预动作时间仿真数据分析
对乘客人群密度从0.08~2.4人/m2进行仿真.选取8个人群密度值进行仿真,分别是0.08,0.40,0.72,1.04,1.36,1.60,1.92,2.40人/m2.对每一个人群密度都进行25次仿真实验,取平均值为仿真结果.表1为乘客人群密度为0.08人/m2时的仿真实验结果.
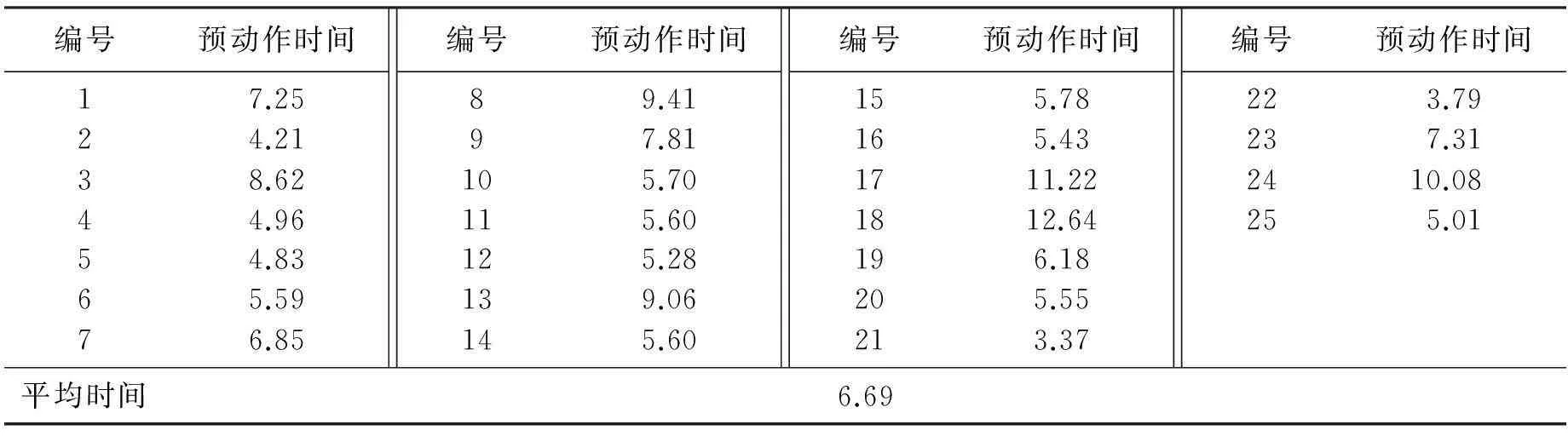
表1 人群密度为0.08人/m2时实验结果
通过表1可以看出,当城市轨道交通站点的人群密度为0.08人/m2时,火灾疏散时的预动作时间均值为6.69 s.其中用时最多的是第18组的12.64 s,用时最少的是21组的3.37 s,标准差为2.26.
采用同样方法,对上述8种人群密度仿真计算,其预动作时间结果如表2所示.

表2 不同人群密度下的预动作时间
根据表2的数据得出的不同人群密度下的预动作时间折线图,如图5所示.
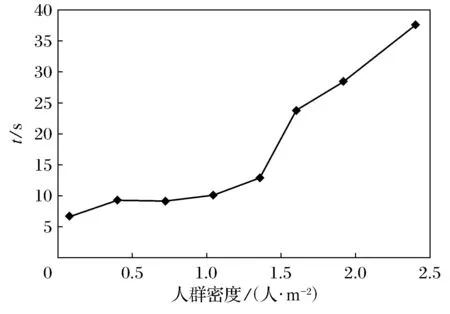
图5 人群密度与预动作时间关系图
由图5可以看出,预动作时间与乘客的人群密度呈正相关.当乘客人群密度从0.08人/m2增加到1.04人/m2时,预动作时间缓慢增加,从6.69 s增加到10.02 s,增幅为52.47%.当人群密度超过1.04人/m2之后,预动作时间迅速增加.当达到1.6人/m2,预动作时间为23.68 s,与人群密度为0.08人/m2时相比,增幅达到253.96%.当人群密度达到1.92人/m2时,预动作时间为28.46 s,是人群密度为0.08人/m2时的4.25倍,远高于人群密度为1.6人/m2时的增幅.
根据图5还可以得出预动作时间曲线的增速不是固定的,当乘客密度处于0.08~1.04人/m2之间的时候,曲线处于一个较为平稳的状态,增幅不明显,预动作时间围绕着10 s上下波动.而0.08~1.04人/m2的人群密度范围,又是城市轨道交通站点常规的人群密度,所以这个数据具有一定参考价值.即在日常乘客数量不多的时候,可以认为乘客的预动作时间即为10 s左右.但是随着乘客密度超过1.04人/m2之后,曲线的增幅明显增加,增速变快.例如当乘客密度为0.08人/m2时,需要的预动作时间为6.69 s,若密度增加至1.04人/m2,预动作时间将会增加至10 s左右,增加的预动作时间约为3 s;但当乘客密度为1.6人/m2时,需要的预动作时间为23.68 s;再将密度增加至2.4人/m2,预动作时间将会增加至37.68 s,增加的预动作时间约为14 s,远大于3 s.这就表示若城市轨道交通站点由于处于高峰时段接待较大流量的客流时,针对火灾事故的预动作时间将会明显增大,所以需要充分考虑预动作时间,在必须安全疏散时间中要进行计算,并预留出充分的疏散时间.
4结论
本文针对城市轨道交通站点火灾事故疏散时的预动作时间进行研究,利用仿真软件Anylogic进行agent建模,模拟城市轨道交通站点乘客在接收到火灾事故警报广播后的预动作情况.对不同的乘客密度进行仿真实验,发现当城市轨道交通站点的乘客人群密度处于0.08~1.04人/m2之间时,所需的预动作时间为10 s.但是人群密度超过1.04人/m2时,预动作时间的增幅较大,此时需要充分考虑准确的预动作时间数值,以便于乘客能安全顺利的进行疏散工作.
参考文献:
[1] 施毓凤,杨晟,孙力彤. 城市轨道交通的安全管理问题[J]. 城市轨道交通研究, 2003(2):26-28.
(SHI Y F, YANG S, SUN L T. Problems in urban mass transit safety management[J]. Urban Mass Transit, 2003(2):26-28.)
[2] 郭光玲,戴国平,马世杰,等. 地铁火灾研究[J]. 都市快轨交通, 2004(S1).
(GUO G L, DAI G P, MA S J, et al. Study on fire in metro[J]. Urban Rapid Rail Transit, 2004(S1).)
[3] 王卓,贾利民,秦勇. 城市轨道交通应急预案分类方案评价研究[J]. 城市轨道交通研究, 2011,14(7):31-35.
(WANG Z, JIA L M, QIN Y. On the classification of emergency disposal plans in urban rail transit[J]. Urban Mass Transit, 2011,14(7):31-35.)
[4] 张凌云. 基于排队理论与社会力模型的地铁人员疏散及安全预警研究[D]. 北京:首都经济贸易大学, 2010.
(ZHANG L Y. Research on the evacuation and safety warning of metro personnel based on queuing theory and social force model [D]. Beijing: Capital University of Economics and Business, 2010.)
[5] 厉剑. 火灾探测信号处理算法及其性能评估方法研究[D]. 大连: 大连理工大学, 2005. DOI:10.7666/d.y965524.
(LI J. Study on fire signal processing algorithms and performance evaluation methods of algorithms[D]. Dalian: Dalian University of Technology, 2005. DOI:10.7666/d.y965524.)
[6] 袁理明,范维澄. 建筑火灾中人员安全疏散时间的预测[J]. 自然灾害学报, 1997(2):28-33.
(YUAN L M, FAN W C. The prediction of safety evacuationin building fires [J]. Journal of Natural Disasters, 1997(2):28-33.)
(XU X L. On modeling and dynamics analysis of social crowd behavior[D]. Tianjin: Nankai University, 2010. DOI:10.7666/d.y1849138.)
[8] LUKE S, BALAN G C, PANAIT L, et al. MASON: A Java multi-agent simulation library[C]∥Proceedings of Agent 2003 Conference on Challenges in Social Simulation. 2003.
[9] 李剑. 多层地下交通枢纽行人疏散分析影响因素研究[D]. 北京: 北京建筑工程学院, 2012.
(LI J. Research on influencing factor of multi-storey underground transport hub evacuation analysis[D]. Beijing: Beijing University of Civil Engineering and Architecture, 2012.)
[10] 汪金辉,金泽阳,田镇纲,等. 学校公众聚集场所火灾中人员疏散预动作时间试验[J]. 科技导报, 2012(11):57-60.
(WANG J H, JIN Z Y, TIAN Z G, et al. Pre-evacuation time experiment in public assembly occupancy of school under the fire[J]. Science & Technology Review, 2012(11):57-60.)
【责任编辑: 王颖】
Calculation about Time of Pre-Action with Fire Evacuation in Urban Rail Transit Station
LinMing,XuHuichuan,JinHua
(Police Information Engineering School, Chinese People’s Public Security University, Beijing 102600, China)
Abstract:With the present situation that fire accident of urban rail transit at home and abroad are frequent, the relationship between the time of pre-action with fire evacuation and the density of passengers’ population is reearched. Anylogic software is used for Agent modeling, the passengers are divided into two categories, and let them communicate about the disaster information with each other. The crowd density is changed in the simulation experiment to observe the different of the pre-action time. The simulation results show that the variation on time of the pre-action is slight when the crowd density is 0.08~1.04人/m2, but the amplification of the pre-action time will increase when the crowd density is 1.04~2.40人/m2.
Key words:urban rail transit; pre-action time; crowd density; fire disaster; evacuation
DOI:[7] 徐旭林. 社会群体行为建模及其动力学分析[D]. 天津: 南开大学, 2010. 10.7666/d.y1849138.
中图分类号:TU 998.1; U 231
文献标志码:A
文章编号:2095-5456(2016)01-0082-05
作者简介:林铭(1990-),男,福建福州人,中国人民公安大学硕士研究生.
基金项目:北京市中央高校共建项目-青年英才计划资助项目(YEPT1367).
收稿日期:2015-07-26

