基于容积卡尔曼滤波的辅助粒子滤波算法

赵　彬，李　炯,曹　艳，赵丹丹

(1.空军工程大学防空反导学院，陕西 西安 710051；

2.陕西师范大学计算机科学学院，陕西 西安 710062)



基于容积卡尔曼滤波的辅助粒子滤波算法

赵彬1，李炯1,曹艳1，赵丹丹2

(1.空军工程大学防空反导学院，陕西 西安 710051；

2.陕西师范大学计算机科学学院，陕西 西安 710062)

摘要:针对非线性系统的状态估计精度较低的问题，提出基于容积卡尔曼滤波(CKF)的辅助粒子滤波(APF)算法—CAPF算法。该算法采用容积数值积分原则计算非线性函数的均值和方差，生成粒子滤波算法的重要性密度函数，获得所需的带权值粒子，进而计算粒子均值，获得系统状态的最小均方误差估计。CAPF算法由于使用最新的量测信息产生粒子，因而提高了对系统状态估计的逼近程度。仿真结果表明，CAPF算法具有更高的滤波精度，验证了算法的可行性和有效性。

关键词:非线性系统；容积卡尔曼滤波；辅助粒子滤波；重要性密度函数

0引言

自1960年，kalman提出卡尔曼滤波算法以来，各种改进的滤波算法层出不穷，研究热点也从线性高斯问题向非线性非高斯问题转移。由于现实世界里，非线性滤波问题更为普遍，对于该问题的研究具有更大的应用价值。当前，在众多的应用领域中，目标跟踪一直是研究的热点，基于经典卡尔曼的改进算法，如解决非线性滤波的扩展卡尔曼滤波算法(EKF)[1]，无迹卡尔曼滤波(UKF)[2]，容积卡尔曼滤波算法(CKF)[3]，这些算法在视频跟踪和雷达跟踪中都取得了较好的应用效果，基于此的改进算法还在不断被推演，但本质上都是卡尔曼滤波思想。另一种解决非线性滤波问题的著名方法是序贯蒙特卡罗方法(SMC)，即粒子滤波算法(PF)，该方法是用一组离散随机采样点(粒子)来近似系统随机变量的概率密度函数，使用这一近似的表示来估计非线性系统的状态。对于粒子滤波的研究，主要在于有效地解决粒子退化的问题，以期达到较好的滤波效果。文献[4]提出一种基于扩展Η∞滤波(EHF)产生重要性函数的粒子滤波算法，由其产生的重要性函数更接近于系统状态的真实后验概率分布。文献[5]对典型的四种改进的粒子滤波算法做了比较，分析了各自的优缺点，其中辅助粒子滤波算法(APF)在高误差的影响下改善效果虽然不如不敏粒子滤波算法(UPF)，但是由于其使用两次加权操作，产生的粒子权值比采样重要再采样(SIR)滤波产生的粒子权值变化更稳定，得到的估计结果也更准确。

上述算法对粒子退化只是进行了单一方面的改善，不能较好地改善粒子退化问题，本文针对此问题，提出基于CKF 的APF算法-CAPF算法。

1CKF算法

CKF是一种滤波精度高，不需微分的滤波算法，采用一组等权值的Cubature点集来解决贝叶斯滤波的积分问题，它使用的容积点的个数少，运行时间短，比传统的UKF和EKF算法具有更好的非线性逼近功能、数值精度以及滤波稳定性[6]。

CKF滤波的具体步骤如下：

1)状态更新

计算容积点：

(1)

传播求容积点：

(2)

状态预测：

(3)

状态预测协方差矩阵：

(4)

2)量测更新

计算求容积点：

(5)

传播求容积点：

Zi,k|k-1=h(Xi,k|k-1)

(6)

计算观测预测值：

(7)

计算观测预测协方差矩阵：

(8)

计算互协方差矩阵：

(9)

计算卡尔曼增益：

Kk=Pxz,k|k-1P-1zz,k|k-1

(10)

状态更新：

(11)

状态协方差矩阵更新：

(12)

2APF算法及其改进算法

2.1APF算法

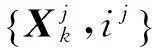
p(Xk,i|Zk)∝p(Zk|Xk)p(Xk,i|Zk-1)=

(13)

(14)

q(X,i|Zk)=q(i|Zk)q(Xk|i,Zk)

(15)

由式(14)可得

(16)

(17)

与SIR滤波相比，APF的优点在于使用两次加权操作，使生成的粒子权值比通过SIR滤波生成的粒子权值变化更稳定，得到的估计结果更准确。

具体算法步骤[7]如下：

为了实现粒子滤波算法，选择重要性密度函数是关键问题之一，本文采用算法性能比UKF和EKF更好的CKF算法来产生重要性密度函数，获得新的粒子滤波算法——CAPF算法。该算法的描述如下：

1)初始化(k=0)，依据先验条件概率抽样:

(18)

2)对于k=1,2,…，用CKF设计的重要性函数:

(19)

3)重要性采样，当i=1,2,…,N，用CKF更新每个粒子；重新产生粒子：

(20)

依据APF算法中的步骤3)计算权值并进行归一化处理；

5)计算状态估计值：

(21)

(22)

6)根据得到的新粒子状态值、方差阵和模型概率，重复以上步骤进行下一次的滤波计算。

3仿真分析

这里采用一个广泛的算例对CAPF算法在非线性系统中的应用进行仿真分析。其状态模型和观测模型为：

xk=fk(xk-1,k)+wk-1

(23)

(24)

图1　两种算法对目标状态估计Fig.1　Target state estimate of two algorithms

图2　跟踪位置误差对比Fig.2　Error of tracking

图3　APF下粒子权值概率密度Fig.3　particle weight probability density of APF

图4　CAPF下粒子权值概率密度Fig.4　particle weight probability density of CAPF

从图1可以看出，通过APF滤波和CAPF滤波虽然都能逼近真实状态值，但是CAPF滤波算法的逼近程度更好一些。

为了描述本文算法的估计质量，采用状态估计误差标准差(Error Standard Deviation,ESD)来评估，表达式为：

表1　两种滤波算法的平均ESD

根据误差理论[8]，CAPF算法相对APF算法提高的滤波精度可以计算为：

通常选取合适的重要性函数可以减小误差，在这里，使用容积卡尔曼滤波(CKF)算法来产生的重要性密度函数表现了较好的滤波性能。

现有粒子滤波算法几乎都是对所有粒子进行的完全重采样，这种“过渡”重采样极易引起粒子贫化[9]。图3和图4分别为APF下和CAPF下粒子权值概率密度，从两图中可以看出，APF下的粒子退化严重，粒子有效权值的概率密度在重采样后减小，而在CAPF下，由于使用了CKF产生的重要性函数，粒子有效权值的概率密度在重采样后依然保持了较好的状态分布。

4结论

本文提出了基于CKF的辅助粒子滤波算法。该算法将CKF算法与APF算法结合，运用容积数值积分方法产生重要性密度函数，获得所需的带权粒子，结合APF的粒子权值变化的稳定性以及估计结果的准确性的特点。仿真验证表明CAPF算法具有更高的滤波精度。

参考文献:

[1]Doucet A, Johansen A.A tutorial on particle filtering and smoothing: Fifteen years later[M] //Crisan D, Rozovskii B eds. TheOxford Handbook of Nonliner Filtering. New York: Oxford University Press, 2011:656-704.

[2]Sarkka S. Bayesian Filtering and Smoothing[M].Cambridge: Cambridge University Press,2013.

[3]Ienkaran A, Simon H, Robert J E. Discrete-time nonlinear filtering algorithms using Gauss-Hermite quadrature[J]. Proceedings of the IEEE，2007,95(5):953-977.

[4]万洋,王首勇,于兴伟. 一种扩展Η∞粒子滤波方法[J].信号处理,2010,26(6):869-874.

[5]张淼,胡建旺,周云峰,等. 改进粒子滤波算法的比较[J].电光与控制,2009,2(2):30-32.

[6]陈海，单甘霖. 基于IMMCKF的机动目标跟踪算法[J].电光与控制，2011,18(10):1-5.

[7]赵梅，张三同，朱刚. 辅助粒子滤波算法及仿真举例[J].北京交通大学学报，2006,(4):24-28.

欢迎订阅《探测与控制学报》

《探测与控制学报》是由西安机电信息技术研究所、机电动态控制重点实验室、中国兵工学会联合主办的国内外公开发行的学术期刊。1979年创刊，被中文核心期刊要目总览、中国科技核心期刊收录，也是中国科学引文数据库来源刊。本刊是综合性的学术技术刊物，旨在为引信及相关探测与控制技术领域内的科研、生产和教学服务，重点刊载：机、电接触探测，无线电、红外、激光和磁近程探测，信号处理，超小型电源，安全与解除保险装置，测试仿真等方面的学术论文。

《探测与控制学报》为双月刊，每册15元，全年90元。刊号：ISSN 1008-1194；CN 61-1316/TJ，欢迎各单位及读者订阅。

联系人：庞彦波电话：029-88156204邮箱：tcykz@263.net

Auxiliary Particle Filter Based on Cubature Kalman Filter

ZHAO Bin1, LI Jiong1, CAO Yan1, ZHAO Dandan2

(1.Air and Missile Defense College, Air Force Engineering University, Xi’an 710051,China;2.School of Computer Science, Shaanxi Nomal University, Xi’an 710062, China)

Abstract:A new particle filter of APF algorithm based CKF(CAPF) was proposed to improve the low state estimation accuracy for nonlinear systems. The algorithm used the cubature rule based numerical integration method to calculate the mean and covariance, to generate the important density function for the particle filter, and to obtain the required particles with weights. Then the minimum square error state estimation is obtained. CAPF algorithm generates particles using the latest measurements so that the approximation to the system state. Simulation results showed that the algorithm was of higher accuracy of CAPF, and also verified the feasibility and effectiveness of the algorithm.

Key words:nonlinear system; cubature Kalman filters; auxiliary particle filter; important density function

中图分类号:TP391

文献标志码:A

文章编号：1008-1194(2016)01-0109-04

作者简介:赵彬(1988—)，男，河南商丘人，硕士研究生，研究方向：高速高机动目标跟踪算法。E-mail：zhaobinhit@qq.com。

基金项目:航空科学基金项目资助(20130196004)

*收稿日期:2015-09-21