基于贝叶斯诊断理论的航空发动机燃气涡轮机故障原因分析

王晓钢，刘振岗，邹　刚，范　兴，刘治国，郭　刚

(海军航空工程学院青岛校区 航空机械系，山东 青岛 266041)



基于贝叶斯诊断理论的航空发动机燃气涡轮机故障原因分析

王晓钢，刘振岗，邹刚，范兴，刘治国，郭刚

(海军航空工程学院青岛校区 航空机械系，山东 青岛 266041)

摘要：将贝叶斯数值理论应用到航空发动机燃气涡轮机的故障诊断过程中，通过建立燃气涡轮机贝叶斯数值诊断理论模型，计算出系统所表现出的故障征兆对故障成因的概率，利用状态识别极限法则，来判定涡轮机系统所处的工作状态。经过长期实践验证，此方法具有良好的故障诊断、识别效果，有效提高了该型燃气涡轮机故障诊断过程中不确定性信息处理的能力及推理的质量。

关键词：航空发动机；燃气涡轮机；贝叶斯理论；故障诊断

燃气涡轮机是航空发动机最为重要、核心的部件，它在整个发动机系统故障诊断中处于举足轻重的地位。在我海军航空兵外场工程实践中，发动机燃气涡轮机故障诊断主要通过分析所采集到的故障征兆来判断故障原因及相应类型，是一个从征兆到故障成因较为复杂推理之过程[1]。在工程实践中，故障成因与征兆之间并不是一一对应的关系，一种故障成因可产生多种征兆, 而一种征兆也可能同时与几种故障成因相对应[2]。其次，机务人员所获故障信息的质量会受到现场环境及测试条件等多种因素限制，常常需所依据的信息不完整、不确定的情况下进行分析与诊断[3]。某种程度而言，目前我军外场航空涡轮起动机系统故障诊断基本上还是依赖排故人员主观经验的识别。贝叶斯网络是一种基于概率的不确定性推理网络，最早是由Judea Pear于1988年提出，当时主要用来处理人工智能中的不确定性信息[4]。

近年来，贝叶斯网络得到了不断的改进与发展，使它作为不确定性推理的有力工具，己成功应用于计算机智能科学、医疗诊断和工业控制等众多领域[5]。燃气涡轮起动机故障诊断实质上也为一个不确定的推理过程[6]，因此本文将贝叶斯数值理论技术应用到航空发动机燃气涡轮起动机系统的故障诊断分析过程中，判定该系统所处的工作状态。

1贝叶斯数值诊断模型建立

贝叶斯诊断方法是在贝叶斯公式基础上发展起来的一种统计诊断方法。这种方法具有简单易行、效果好的优点，但是所需的预备信息量大，如果积累的统计资料足够，这种方法不失为可靠而有效的方法[7]。

假定机器或系统在运行中可能处于n个(D1、D2、D3…Dn)状态之一，在这些可能的状态中只有一个状态是正常的状态，其余的状态下机器均存在缺陷。在实践中一般假设状态Di与Dj是互相排斥的，即机器或系统在检测时只能处于一种状态，不能同时处于几种状态。如果机器可能处于多种状态，那么还要考虑这些状态的组合Dr+1=D1∧D2……等[8]。

机器处于状态Di的概率是由积累的统计资料或人的经验来决定的，所以称为先验概率。例如，在检测了N台机器后，统计有Ni台机器处于状态Di，那么P(Di)=Ni/N，并且有：

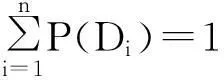
(1)

进一步考虑，当机器处于某个状态Di时可能具有特征P(Kj│Di)(称为条件概率)，这一组条件概率：

P(Kj│D1)，P(Kj│D2)，P(Kj│D3)，…，P(Kj│Dn)

(2)

也是从实际检测机器的运行状况中得到的。例如，当检测Ni台处于Di状态的机器之后，统计到其中有Nj台具有Kj特征，则：

P(Kj│Di)= Nj/ Ni

(3)

这样，机器处于状态Di并且具有特征Kj的复合概率为：

P(DiKj)= P(Di)P(Kj│Di)

(4)

同理：P(DiKj)= P(Kj)P(Di│Kj)

(5)

其中条件概率P(Di│Kj)的意义是“通过检测发现机器或系统具有特征Kj，则机器或系统处于状态Di的概率”。从以上两式中解条件概率P(Di│Kj)得到：

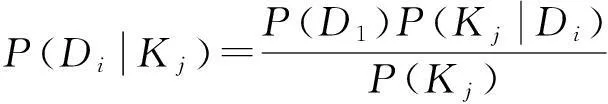
(6)

这里P(Kj)是在所有的机器中(不论这些机器的状态如何)出现特征Kj的概率。如果在总数为N的机器中检测其中有Nj台机器具有特征Kj，则

P(Kj)= Nj/ N

(7)

但是这里的P(Kj)不需要专门通过统计得到。事实上通过全部P(Di)和P(Kj│Di)的值，即可求出P(Kj)

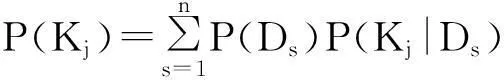
(8)

这是因为特征Kj总是伴随着一个状态，而且只有一个状态Di出现的缘故。代入上面的公式得：

(9)

这里P(Di│Kj)是经过计算得到的，在实验结束可以修正的概率，称为后验概率。贝叶斯公式回答了这样一个问题：当机器或者系统实际上具有特征Kj时，它由先验概率P(Di)表述了后验概率P(Di│Kj)。

一般说来，通过检测所得到的机器特征往往是定量的，例如温度、压力等参数；有时还可能是连续变量，而这里的特征只能是定性的描述。为解决这个矛盾，应该把检测的参数划分为区间。例如，排气温度高于500℃和低于500℃两个区间，当机器的实际排气温度高于500℃，我们说机器出现特征Kj；而当机器的实际排气温度低于500℃时，则认为机器无此特征。

在多数情况下机器同时具有多个特征，并且特征之间往往是互相独立的。即使有的特征之间存在某些相关的联系，仍可把它们当作相互独立的特征来考虑。这时我们可以用特征集合K =(K1，K2，…，Km)来检测机器的状态，可写为

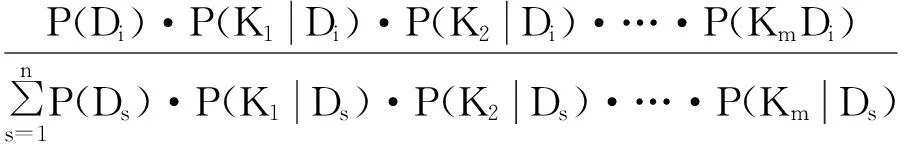
(10)

为了用上式确定机器所处的状态，首先应作出诊断矩阵(见表1)。此诊断矩阵是由累积的统计资料形成的，表中列举了机器处于不同状态时各个特征区间出现的概率。最简单的特征是只在两个区间的有和无。如果特征具有多个区间1，2，…，mj，则应填入状态Di下相应特征区间的概率P(Kj1│Di)，P(Kj2│Di)，…，P(Kjmj│Di)，并且有：

(11)

如表1所示。

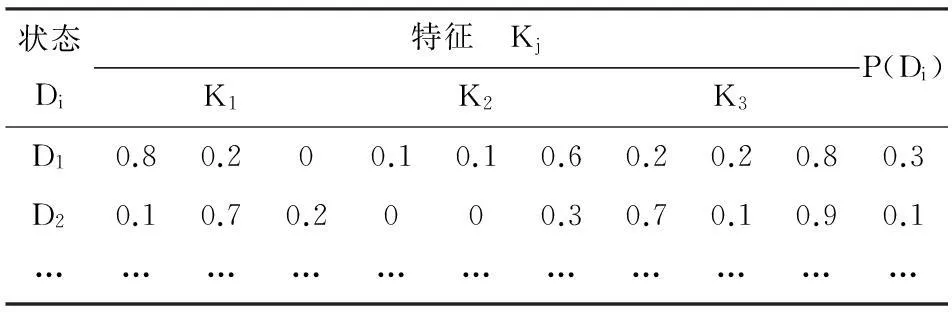
表1　机器状态Di下相应特征区间概率

2贝叶斯数值诊断模型在燃气涡轮机系统故障中识别及应用

自2002年以来，海军航空兵部队机务人员在实际外场工作过程中，经过大量数据统计，该型号发动机的燃气涡轮起动机共计发生故障412次，该燃气涡轮机主要有两个特征：

K1——机器的排气温度高于500℃；

K2——超过最高转速的持续时间大于5秒。

假定对于这种燃气涡轮机而言出现这些特征或者是燃油调节器工作失调(状态D1)，或者是由于机器的径向间隙增加(状态D2)。在正常状态(D3)下特征K1出现的概率为0，特征K2出现的概率为0.05。

在状态D1下特征K1出现的概率为0.2，K2为0.3。在状态D2下K1为0.4，K2为0.5。同时统计资料表明：此类发动机80%在正常状态D3下工作，5%在D1下工作，15%在D2下工作。

首先将已知数据填入诊断矩阵表中，如表2所示。

表2　燃气涡轮机状态Di下相应特征区间概率

下面确定当发动机同时具有两个特征K1和K2的情况下机器处于各种状态的概率。假定两个特征是相互独立的，由(9)得：

=0.09

同理可以求得：

=0.91

=0

=0.12

同样方法求出：

=0.46

=0.41

进一步计算当两个特征均不存在时，机器的状态概率为：

=0.08

并且有：

=0.05

=0.92

在贝叶斯诊断方法中应该如何根据式(8)和(9)所计算出的状态概率来判断机器或系统所处的状态呢？如果通过检测证实机器具有特征K，那么判断机器所处的状态应该以概率最大的状态为机器状态。用数学的方式表达是：

如果P(Di│K)>P(Dj│Ki)，(i，j=1，2，…，n；i≠j)

则有K∈Di

(12)

即特征K应归属于状态Di。显然这种判别方法有一定的错误，为保证诊断结果足够精确，引入一个状态识别限Pi，应保证

P(Di│K)≥Pi

(13)

其中Pi是预先选定的对其状态Di的识别限，并且要求其它状态的概率不能大于1-Pi，一般取Pi≥0.9。反之，如果计算的结果不能满足上述条件，如上例中机器具有特征K2但不具有特征K1的情况，即P(Di│K)

由以上计算看出，当机器同时具有特征K1和K2时，状态D1(即径向间隙增大)的概率为0.91；当机器中的两个特征都不存在时，机器处于正常状态D3的概率为0.92；当机器不具有特征K1但有特征K2时，机器处于D2和D3的概率大致相等。为进一步在这种情况下判断发动机所处的状态，应对海军航空兵近13年燃气涡轮起动机所发生的故障进行分析。

在上述的412次故障中，当燃气涡轮起动机系统同时出现排气温度高于500℃(即特征K1)；与超过最高转速的持续时间大于5秒(即特征K2)时的征兆206起，经过排故人员排查，处于燃油调节器工作失调(状态D1)的次数为175次，概率为0.85，与理论计算值误差为7.7﹪，在误差允许范围之内。

当燃气涡轮机的两个特征，即排气温度高于500℃，与超过最高转速的持续时间大于5秒均无出现时，此时燃气涡轮机基本均处于正常状态，与理论计算概率0.92基本吻相符合。

当燃气涡轮机具备特征K2，但不具备特征K1时，燃气涡轮起动机处于正常状态为186起，而处于径向间隙增加为176起，误差为5.4﹪，基本上比例相当，在误差允许范围之内，与数值理论模型计算相吻合。

3结论

本文主要将贝叶斯数值诊断方法应用到某型航空发动机燃气涡轮机系统故障诊断过程中，通过建立燃气涡轮机贝叶斯数值诊断理论模型，计算出系统所表现出的故障征兆对故障成因的概率，即文中的燃气涡轮机的状态概率或先验概率和全部的条件概率P(K│Di)基础上，来确定和判断P(Di│K)，即在实际检测到机器具有特征K后处于Di状态的概率。即为通过先验概率求出后验概率，利用状态识别极限法则，来判定涡轮机系统所处的工作状态。最后，将理论计算结果与我海军航空兵近13年以来的外场大量数据统计进行对比分析，理论计算与实践检验基本相吻合，误差均在允许的范围之内。贝叶斯数值故障诊断方法经过长期实践验证，此方法具有良好的故障诊断、识别效果，有效提高了该型燃气涡轮机故障诊断过程中对不确定性信息的处理能力及推理的质量，对我海军航空兵航空发动机相关领域故障诊断及排除方面起到积极的推动与促进作用。

参考文献

[1] 史志富，张安.贝叶斯网络理论及其在军事系统中的应用[M].北京:国防工业出版社,2012：35-38.

[2] 程延伟,谢永成,李光升,等.基于贝叶斯网络的车辆电源系统故障诊断方法[J].计算机工程,2011,37(23):251-253.

[3] LI L,SUN Y K,LI Y M.A new fuzzy fault diagnosis method[C]//Proceedings 5th International Conference on Fuzzy Systems and Knowledg Discovery,Shandong,China,2008,3:479-483.

[4] 任佳，高晓光.贝叶斯网络参数学习及对无人机的决策支持[M].北京:国防工业出版社，2012:112-115.

[5] 肖琴琨，高嵩.贝叶斯网络在智能信息处理中的应用[M].北京:国防工业出版社,2012:69-73.

[6] Sala A,Ramirez J C,Tormos B,et al.An optimization approach to fuzzy diagnosis:Oil analysis application[C]//IEEE International Conference on Fuzzy Systems,London,England,2007:1-6.

[7] 王浩，高金吉，江志农，等.基于案例推理的旋转机械故障诊断系统研究[J].科学技术与工程，2012(29)：7585-7591.

[8] 王伟，赵卫强，刘永贤.基于模糊诊断原理的航空液压油泵车故障诊断系统的研究[J].沈阳航空航天大学学报，2012(4)：42-46.

[责任编辑、校对：东艳]

Analysis of Malfunction Causes of Aerial Engine Gas Turbine Based on Bayesian Diagnosis Theory

WANGXiao-gang,LIUZhen-gang,ZOUGang,FANXing,LIUZhi-guo,GUOGang

(Department of Aviation Mechanics,Qingdao Campus,Naval Aeronautical Engineering Institute,Qingdao 266041,China)

Abstract：Bayesian numerical theory is applied to the malfunction diagnosis process of aerial starter motor gas turbine in this text.The numerical theory model of Bayesian malfunction diagnosis of gas turbine is established.The probability of malfunction foreboding that shows to the cause of system is calculated,and the status identification extreme rule is utilized to judge the working status of the turbine engine system.The long-time outfield practice verifies that this method is effective in malfunction diagnosis and identification,and increasing the uncertainly information disposal competence and inferential quality of motor starter gas turbine malfunction diagnose process.

Key words：aerial engine;gas turbine;Bayesian theory;malfunction diagnosis

中图分类号：V263.6

文献标识码：A

文章编号：1008-9233(2016)01-0003-04

作者简介：王晓钢(1979-)，男，吉林榆树人，讲师，从事智能监测与控制、航空飞行器故障诊断研究。

收稿日期：2015-11-03