借助信息技术实现高效课堂的三个“着眼点”

崔玉兰

【关键词】信息技术 高效课堂

着眼点

【中图分类号】G 【文献标识码】A

【文章编号】0450-9889（2016）02A-0006-02

在加快推进教育现代化的今天，信息技术改变了教育、改变了课堂。如何借助信息技术实现高效课堂，已成为当前教育工作者深入探讨的热点问题。为此，笔者主持申报了福建“十二五”教育规划重点课题“信息技术环境下小学数学高效课堂的教学策略的研究”，获得了省教科所的立项。在该课题研究中，笔者针对当前小学数学课堂教学中的“低效”现象进行了归因分析，总结出借助信息技术实现高效课堂的三个“着眼点”。下面结合教学实践谈谈自己的思考。

一、着眼于学生思维的“崎岖处”

在数学学习过程中，学生知识的接受、能力的发展，离不开经验的有力支撑。但仅凭经验，有时还是会力不从心，特别是一些比较抽象的数学知识，往往会存在一些困难。此时，教师要借助多媒体课件，形象直观地对学生思考的维度加以点拨，扶着学生前行，让学生走出思维的“崎岖处”。如人教版小学数学五年级下册《探索图形》一课，要探索出图形中的规律，对于五年级学生而言，极具挑战性。在棱长为2、棱长为3的正方体中，每个小正方体的涂色情况，大部分学生得到个数都是在观察中数出来的，没有意识到每一类涂色的数量存在一定的规律。所以，在探索棱长为4的正方体的涂色情况时，很多学生会对一面涂色和没有涂色的小正方体的个数产生分歧，还有的学生甚至不知从何入手。如果通过动手操作验证，一则拆分之后数量多、零散，不利于空间观念的培养;二则课堂时间有限，将无法完成教学任务。于是，笔者这样展开教学：

先借助课件动态展示每条棱上去掉顶点处的两个三面涂色，每条棱上就剩（4-2）个两面涂色，12条棱就有（4-2）×12=24（个）;

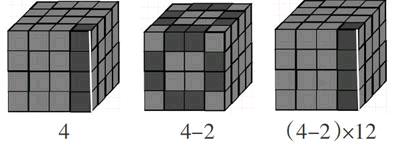
再次动态播放大正方体剥离左右两列，上下两行的课件，使学生清晰地看到每个面上一面涂色的小正方体的个数是（4-2）2个，6个面就有（4-2）2×6=24（个）;

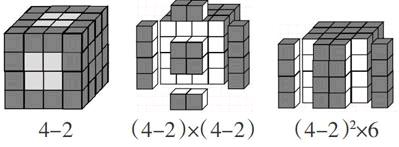
最后根据学生的回答同步播放课件：正方体去掉上下两层，左右两层，前后两层有涂色的小正方体个数，剩下的就是中间没有涂色的个数有（4-2）3=8（个）。

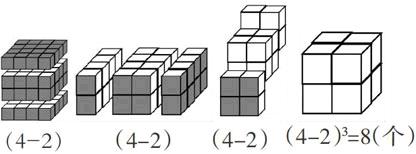
这样教学，既能帮助学生消除疑虑，又为学生探索小正方体的涂色个数的规律提供了思维的“拐杖”。正所谓“数形结合百般好，隔离分家万事休”，教师充分利用课件，从两面涂色的位置特征和求个数来源入手，声情并茂地展现一面涂色和没有涂色的个数的位置及计算方法，借助数形结合的直观性，解释抽象的数学原理和事实，使学生一目了然。学生在经历知识的生成、发展过程中，体会知识的来龙去脉，从直观到抽象，从特殊到一般，从“数”到“算”，发现规律，再利用规律推理出更多更大乃至棱长为n的正方体的涂色情况，初步建立各种涂色情况个数的计算模型，高效完成学习任务。这样教学，不仅培养了学生的推理归纳能力，感悟了数形结合、模型、对应等数学思想，还进一步发展了学生的空间观念，增强了学生的空间想象能力。

二、着眼于学生思维的“拐弯点”

一直以来，静态的数学教材与学生动态的数学生成成为了学习过程中的矛盾。特别是一些相似的数学知识，学生往往容易出现认知上的混淆，一时难以区分。如果仅仅凭借静态的教材呈现和教师的说教，学生常常难以理解或接受。此时，如果能借助现代信息技术手段，加上教师正确的引导，不仅能实现课堂省时、高效，还会让学生的“思维”成功拐弯。如人教版小学数学二年级下册《轴对称》一课，学生认知上的难点是辨别轴对称图形。特别是图形的左右或上下两边完全一样时，很多学生会认为一定是轴对称图形。之所以有这样的错误认识，是因为他们认为只要图形中有完全相同的两部分，这两部分就能完全重合。前期，在我校课题实验阶段性成果汇报时，就以本课内容进行“同课异构”，其中一位老师在这个难点的处理上就恰如其分。教师借助现代信息技术手段，采用现代信息技术——电子书包即一对一教学互动模式，在初步认识轴对称图形的基础上，出示以下一组图片，让学生在电子书包中选一选：哪些是对称图形，哪些不是？

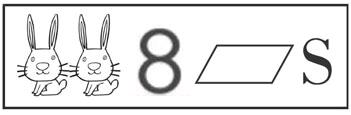
电子书包的自动汇报系统显示第一幅兔子图学生的完成情况，认为是对称图形有34人，认为不是对称图形有16人。当持有这两种不同答案的学生分别说明理由并争执不下时，教师提出：想不想动手折一折？让我们眼见为实。请大家点击电子书包屏幕下方的“对折键”——“①”，仔细观察，你看到什么？学生兴致勃勃地在各自的电子书包上操作，清晰地看到虽然兔子图左右两边完全一样，但对折后不能完全重合，所以不是对称图形。原来认知错误的学生恍然大悟，左右两边完全相同的图形不一定是对称图形。到底怎样才能判断一个图形是不是对称图形呢？教师再次充分利用资源，引导学生思考：怎样才能使兔子图变为对称图形呢？在学生的建议下，教师出示把其中一只兔子的方向调整之后的图形，并引导学生认真观察位置调整后的兔子图是不是对称图形。此时学生都一致认为是对称图形，并在各自的电子书包按“对折键”进行验证。教师再引导学生与之前的兔子图进行了对比，找出异同点，再次澄清了之前的错误认识，形象、直观、真实、高效！学生进一步体会到：判断一个图形是不是对称图形，不能只看左右（或上下）图是不是完全一样，要想象对折之后是不是完全重合，完善对轴对称图形的认识之后，学生再辨别平行四边形是不是对称图形就轻而易举了。

三、着眼于学生思维的“行进地”

数学学习的全过程，是从资源生成到过程生成再到思维拓展的过程。学生在思维拓展的“行进地”，往往也需要借助现代信息技术手段，形象地沟通知识间的联系，延伸知识的内涵，形成清晰化和结构化的认识。在刚刚落幕的第三届闽浙小学数学课堂交流研讨活动中，笔者有幸聆听洪菲菲老师执教的人教版三年级下册《小数的初步认识》一课，在借助“元”“米”初步认识小数的基础上，洪老师设计了“改变‘量再识小数”的环节，巧妙地利用信息技术，直观形象地实现有效教学：首先老师提出问题：“如果现在老师给你一条线段，你能选择一个学过的单位，再用分数、小数表示出来吗？你想选择什么单位？”教师借助Flash软件根据学生的回答在1的后面输入一个“元”字，课件就会在其他的四个括号后面同时出现“元”字，并让学生分别说出每个箭头处所表示的分数、小数各是多少？

接着，教师又提出：还可以选择什么做单位？

课件又出现刚才那条把“1”平均分成10份的线段，根据学生的回答，输入不同的单位，填上不同箭头所指的数。

在此基础上，教师提出质疑：“刚才我们用了不同的单位，把线段上箭头所指的点用分数和小数都表示出来了，那么，第一条线段上的0.4元，能不能放在第二条线段上？”学生把目光再次聚集到课件上，对比三条线段，达成共识：单位不一样，所以不可以。此时，教师把三条线段上的单位名称全部消失之后，学生就异口同声地表示现在就可以了，还发现无论选择哪个单位，只要平均分成10份，其中的几份就可以用零点几来表示，零点几表示的就是十分之几。

然后，洪老师又通过课件动态演示把这三条线段合起来，让学生在这条线段上找到其他的分数和小数。有了形象的经历之后，学生找到其他的分数和小数也就易如反掌了。然而，洪老师并没有就此结束，而是继续追问：0～1之间有多少个这样的小数？一起来数一数。（课件从0.1～0.9逐个闪动）当学生数到9个数时，再次质疑：9个0.1再加一个就变为多少？更出乎大家意料的是，洪老师还继续让学生们在0～1的这条线段上找出自己的身高1.4米。课件再次展现学生的想法：把线段延长并把1～2之间的线段再平均分成10份，1.4是在1和2之间。再引导学生通过想象找3.5，应该在哪两个数之间找？7.4呢？9.8呢？如果老师把这条线段不断延长，上面的小数你能找得完吗？所以就把右端用箭头表示，数轴就这样产生了。

在上述案例中，洪老师充分利用信息技术，使学生对小数的含义有了更深层次的认识。先是通过换上不同的计量单位再找小数、写小数，让学生感悟到变的是“量”，不变的是小数的意义，从有“量”到无“量”提高学生对小数的纵向认识;再借助数轴的直观作用，学生在数小数的过程中，对“十进制”关系有了初步的体验;最后借助数轴的无限延伸的特点，学生在“找小数”的过程中，体会到小数与整数的关系，不仅是对小数认识的横向拓展，也将小数纳入原有的数系之中，沟通了小数与分数、整数之间的联系，渗透数形结合、一一对应、极限和变与不变等数学思想。这样不仅拓宽了学生的思维，完善了知识的建构，也让听课老师见识了高容量、高效率的课堂，彰显教师的高水平！

当然，借助信息技术实现高效课堂，不仅要把握这三个“着眼点”，还需要教师戴好一副“近视镜”去了解学生的真实起点，戴好一副“显微镜”去看清数学的内涵本质，戴好一副“望远镜”望得更高看得更远，做到该出手就出手，只有这样，才能体现其价值，真正实现高效课堂。

注：本文系福建省“十二五”教育规划重点课题《信息技术环境下小学数学高效课堂的教学策略的研究》的研究成果（项目编号：FJJK14-314）。

（责编 林 剑）