基于改进人工蜂群算法的共形阵列波束形成

刘超，樊良慧（合肥工业大学计算机与信息学院，安徽合肥　230009）



基于改进人工蜂群算法的共形阵列波束形成

刘超，樊良慧
（合肥工业大学计算机与信息学院，安徽合肥230009）

摘要：针对共形阵列中主瓣约束下的波束形成问题，文章提出了一种基于改进人工蜂群算法（Improved Artificial Bee Colony algorithm，IABC）的低副瓣方向图综合算法。算法首先将共形阵列的波束形成问题归纳为一个与目标方向图距离最小化的优化问题。通过引入多维邻域搜索策略，改善人工蜂群算法的局部搜索效率，同时通过增加罚函数来抑制副瓣电平，对权值矢量空间进行搜索，寻求最优权值矢量，最终得到与期望逼近的阵列方向图。实验结果表明该算法能够很好地逼近期望方向图，收敛速度快，为实现共形阵列下的波束形成提供了有价值的参考。

关键词：共形阵列；波束形成；主瓣赋形；人工蜂群算法；多维邻域搜索

0　引　言

共形阵列天线能够安装在载体平台的曲面表面，具有节约载体平台空间、不影响载体气动特性、降低雷达散射截面积（radar cross section，RCS）、增强隐蔽性、扩大可用口径和波束扫描范围等优点，能够显著提高载体平台的战斗及生存能力，在车辆、飞机、舰船、导弹乃至卫星上都具有广泛的应用前景［1］，因此也受到学者的广泛关注。但是由于共形阵列中各个天线单元方向图不一致，传统平面阵列下的大多数波束形成算法都不再适用。因此，波束形成问题已经成为共形阵列的一项重要研究内容。近年来，许多共形阵列波束形成的相关技术被提出。阵列波束形成问题本质上都可以归纳为一个权值矢量空间中的最优化问题。基于生物学行为所衍生的智能优化算法具有较强的搜索寻优能力，能够灵活地实现多种约束条件下的目标函数优化，为解决该问题提供了一个可行的思路，许多学者将这一类算法引入到波束形成问题中［2］。文献［3］采用对阵元激励矢量的幅度和相位分别进行8位二进制编码的遗传算法（genetic algorithm，GA），并应用于等间距的线阵和矩形阵的低副瓣方向图综合，但是该算法计算复杂，控制参数也较多，收敛速度慢；文献［4］利用粒子群优化算法（particle swarm optimization，PSO）对N维等间距线阵进行方向图综合，实现低副瓣的方向图分布和零陷的控制，然而该算法在解决多参数问题时过早地收敛，难以保持种群多样性；文献［5］对粒子群算法进行了改进，提高了算法的收敛速度；文献［6］首次将蚁群优化算法（ant colonly optimization，ACO）应用于天线阵波束形成，实现不等间距线阵的低副瓣抑制和零陷控制，由于该算法是通过信息素的正反馈找到问题的最优解，所以在搜索初期信息素匮乏，搜索比较盲目，而且该算法计算量大，收敛速度慢。

上述几种方法主要针对平面阵列，目前已经有学者将智能优化类算法应用于共形阵列的波束形成。文献［7］将遗传算法和粒子群算法相结合，利用粒子群算法进行局部搜索，采用遗传算法进行全局搜索，给出一种方向图的混合优化算法。文献［8］提出一种野草算法和粒子群算法的混合优化算法，实现了共形阵列下的低副瓣方向图综合。文献［9］提出多目标粒子群算法（muti-object particle swarm optimization，MOPSO）实现在阵元激励动态范围约束条件下的共形阵列波束形成；并利用WARP（weighted alternating reverse projection）算法求解初始解，提高了多目标粒子群算法的计算效率。但是共形阵列的波束形成问题仍然存在许多需要改进的地方，目前仍然不断有新的方法提出［10-11］。

人工蜂群算法（artificial bee colony，ABC）是2005年由土耳其学者Karaboga提出的模拟蜜蜂群体寻找优质蜜源的一种仿生智能算法［12］。该算法对不同劳动分工的蜜蜂采用不同的搜索策略或模式，通过相互协作共同完成寻优工作。人工蜂群算法作为一种新兴智能优化算法，由于其控制参数少，计算简洁、易于实现。有研究结果表明蜂群算法解决某些复杂问题的性能要优于GA、 ACO和PSO，其应用前景十分广阔［13-14］。

本文对人工蜂群算法进行改进，并应用于共形阵列的波束形成，以实现主瓣赋形下的低副瓣方向图的波束形成。算法将波束形成问题归纳为一个优化问题，通过在适应度函数中设置罚函数来抑制副瓣电平，同时引入多维邻域搜索策略改善算法的局部搜索效率，最终通过人工蜂群的个体并行寻优行为得到阵元激励的最优解。为了验证本文算法的有效性，仿真实验以圆弧阵列为例，实现了笔形波束、平顶波束和余割平方波束3种典型的赋形波束形成。实验结果表明，改进的人工蜂群算法（Improved Artificial Bee Colony algorithm，IABC）能够很好地实现主瓣赋形情况下的共形阵列低副瓣波束形成，收敛速度较快。

1　人工蜂群算法

人工蜂群算法模拟蜜蜂实际采蜜过程，通过不同角色蜜蜂间的交流、转换和协作来实现群体智能［15］。该群体智能搜索模型包含的基本要素有食物源和人工蜂群，其中人工蜂群又分为3种角色：引领蜂、跟随蜂和侦察蜂。2种最基本的行为：为食物源招募蜜蜂和放弃某个食物源。引领蜂和跟随蜂主要进行食物源搜索，侦察蜂则避免食物源种类过少，确保种群多样性。下面给出人工蜂群算法具体实现步骤。

（1）初始化。按（1）式随机生成M个食物源，每一个食物源对应一个引领蜂，并设引领蜂与跟随蜂个数相等。每个食物源wi＝［wi1，wi2，…，wiN］T对应优化问题的一个解，其中N为问题维数。其中，（wij）max、（wij）min为可行解的上限和下限；Rij为［0，1］之间的随机数。

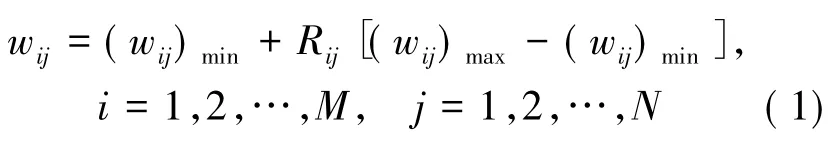
（2）引领蜂。采用“贪婪原则”对相应的食物源按照（2）式进行一次邻域搜索，如果新食物源的食物浓度优于旧食物源，则替换旧食物源，否则保留旧食物源。其中，wkj为随机选择的第k个（k≠i）食物源位置的第j维；rij为［-1，1］上的随机数；vij为更新后的食物源位置。

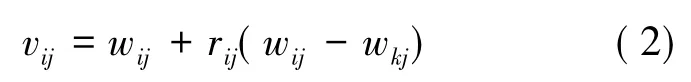
（3）跟随蜂。按照与食物源浓度成正比的概率随机选择一个蜜源，对其进行进一步的邻域搜索，根据食物浓度选择是否替换旧食物源。

（4）侦查蜂。若某食物源的食物浓度连续K次没有被更新，说明该食物源陷入局部最优，放弃该食物源，引领蜂变为侦查蜂，根据（1）式重新生成新的食物源。

（5）结束。记录到目前为止的最优解，重复执行引领蜂、跟随蜂、侦查蜂行为，直到满足结束条件，循环结束。

2　共形阵列波束形成

考虑一个N元共形阵列，其远场方向图可以表示为［10］：

其中，（·）H为矩阵的共轭转置；w＝［w1，w2，…，wN］T为阵元激励矢量；a（θ）为阵列的导向矢量，可以表示为：

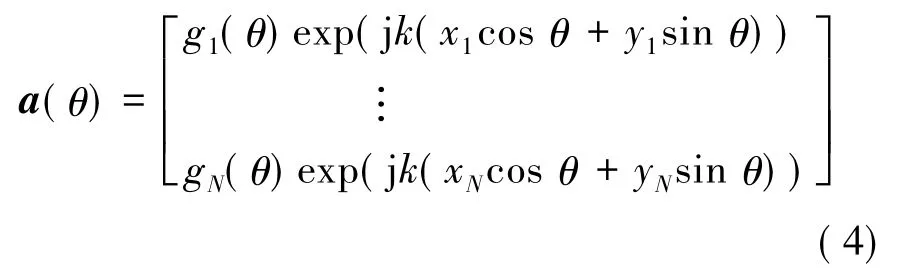
其中，k＝2π/λ为相位常数，λ为波长；gi（θ）为第i个阵元的辐射方向图。

共形阵列的波束形成问题，其本质上是寻求一组合适的阵元激励矢量w使得整个阵列的方向图满足设计的期望。最优的阵元激励矢量可以通过最小化实际方向图与期望方向图之间的误差求得。

假设期望方向图是Ed（θ），那么波束形成问题就可以归纳为期望方向图和实际方向图之间距离最小化的优化问题：

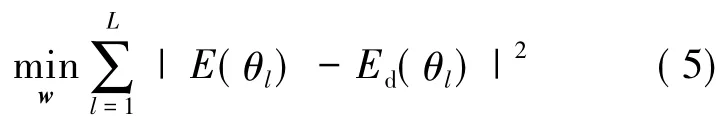
其中，θl为观测角域空间的采样点；L为采样点数。

3　改进人工蜂群算法共形阵列波束形成

在N元共形阵列方向图的优化问题中，食物源的位置相当于阵元激励矢量的一个可行解，食物浓度即为待优化的目标函数。利用人工蜂群算法对可行解空间进行搜索，以得到最优解。

3.1邻域搜索

由（2）式可以看到，每次对一个可行解个体进行邻域搜索，得到的新个体相比于原来的个体只有一个分量更新。共形阵列中，阵元的数目通常较多，考虑到激励为复数，每个可行解个体应该是一个2N维的矢量，因此采用原算法的搜索策略效率不高。针对这个问题，本文对邻域搜索策略进行改进，给出如下的多维搜索策略：

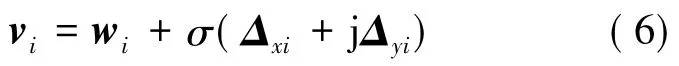
其中，vi为搜索得到的新个体；Δxi、Δyi均为［-1，1］上均匀分布的N维随机矢量；σ为一个较小的正数，用来控制邻域搜索的范围。

3.2适应度函数

适应度函数是用来衡量个体优劣程度的性能指标，直接关系到算法收敛的方向和速度。为了实现赋形波束下的低副瓣方向图，将期望方向图和目标方向图之间的距离作为优化目标。同时为了尽可能压低副瓣电平，将最大副瓣电平作为罚函数引入到适应度函数中。第i个个体的适应度函数为：

其中，SLLmax为最大副瓣电平；α为罚函数系数。

3.3选择算子

常见的选择策略有轮盘赌和锦标赛2种方法，轮盘赌一般用于最大值寻优问题。这里是最小值寻优问题，因此采用锦标赛方法。在种群中随机选择2个个体，比较两者的适应度值，适应度较优（这里是适应度值较小）的个体即为当前选择的个体。

3.4算法步骤

原算法中，侦查蜂行为用来判断某个个体是否陷入局部最优。但实际上，该个体也可能是全局最优。

为了避免全局最优解被丢弃，在侦查蜂行为之前先记录当前最优解，以避免上述情况。具体算法步骤如下：

（1）初始化。确定最大迭代次数Imax、种群规模M、可行解的上下限（wij）max和（wij）min以及控制参数K，根据（1）式产生初始种群。

（2）根据（6）式对每一个个体进行邻域搜索产生新解vi，根据（7）式计算初始解wi和新解vi的适应度函数值并进行比较，如果新解的适应度值优于初始解的适应度值，则用新解vi代替初始解wi，该样本点的搜索次数清零，否则保留初始解wi不变，该个体的搜索次数加1。

（3）采用锦标赛的方法，在种群中随机选择一个个体进行邻域搜索，搜索步骤同步骤（2）。该步骤重复多次，以加强对适应度较高的个体邻域的搜索，提高算法收敛速度。

（4）根据各个个体的适应度值，记录到目前为止的最优解。

（5）判断是否有需要放弃的解。若某个体的搜索次数超过K，那么根据（1）式随机产生一个新的解来替换它。

（6）若循环次数达到最大迭代次数，则终止循环，输出最优解，否则重复步骤（2）～（5）。

4　实验结果分析

仿真实验中采用如图1所示的21元均匀圆弧阵来验证本文算法。整个圆弧对应的圆心角Φ为150°，阵元关于y轴呈对称分布，半径为R＝12λ/π，此时相邻阵元间距大约为λ/2。第n个阵元的方位角为θn，单个阵元的方向图函数为：

在后面的实验中，（7）式中的角域采样间隔取1°，观测角域范围为［0°，180°］，则角域采样点数为L＝181。

图1　均匀分布的N元圆弧形阵列

实验1本文算法与原ABC算法的比较。

主波束宽度为40°，主波束最大值方向θd＝90°，主瓣期望方向图为cos24（θ-θd）。要求主瓣接近期望方向图的同时尽可能压低副瓣电平，由于副瓣不可能无限地被压低，因此在副瓣区域设定一个足够小的期望值来逼近，本实验以及后面的仿真实验中，期望方向图的副瓣电平设为-40 dB。最终得到的阵列方向图的比较结果如图2a所示。

由图2a可以看出，2种方法主瓣都得到了很好的赋形，但副瓣抑制效果不同。原算法和改进算法的最低副瓣电平值分别为-35.563 5 dB和-39.193 0 dB。

图2b所示为收敛曲线比较结果。原ABC算法需要迭代超过2 000次才收敛，而本文给出的IABC算法只需要迭代400次左右就达到收敛。通过本实验可以看出，通过引入多维邻域搜索和罚函数，本文算法在收敛速度上得到了很大的改善，并且副瓣电平的抑制效果也得到进一步改善。

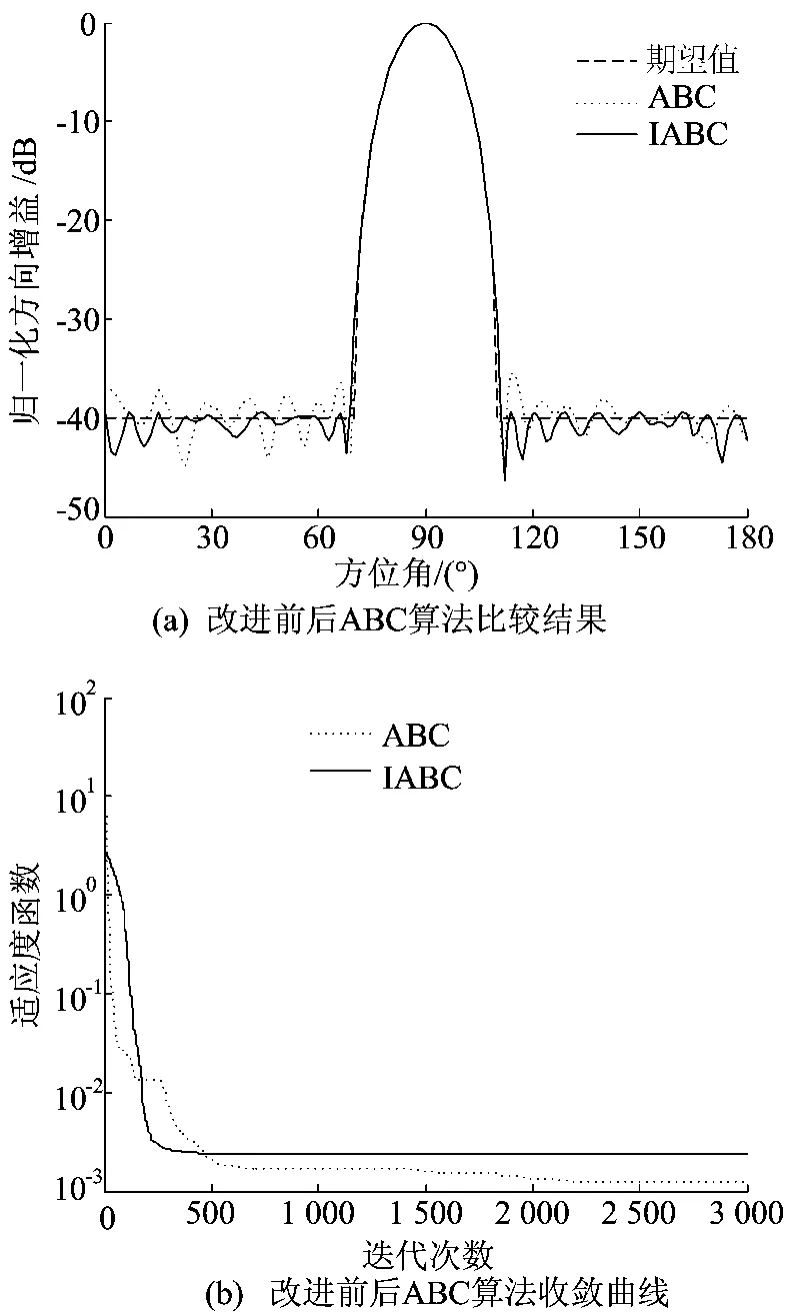
图2　改进前后ABC算法比较结果和收敛曲线

为了进一步验证本文算法的优势，后面的实验选择基于实数编码的GA和标准的PSO作为比较算法，在相同的实验条件下与本文算法进行对比，本文算法简记为IABC。

实验2笔形波束下的低副瓣波束形成。

期望方向图设置同实验1。

蜂群算法具体参数设置：种群规模设为50，控制参数K＝300。算法中步骤（3）重复250次。考虑到GA收敛速度可能较慢，选择最大迭代次数Imax＝3 000。

图3所示为本文算法、PSO和GA的仿真实验结果。

由图3可以看出，在主瓣区域3种算法都能得到较好的赋形结果，而在副瓣区域由IABC得到的方向图的最大副瓣电平比PSO和GA略低一些。

图4所示为3种算法的适应度函数值的收敛曲线，PSO和IABC大概在400次即可达到收敛，而GA要迭代到2 000次才可收敛。

图3　笔形波束方向图

图4　适应度函数收敛曲线

实验3余割平方波束和平顶波束。

余割平方波形和平顶波形也是常用到的波形［16-17］，将期望主瓣波形设为余割平方或者平顶波形，其余实验条件和参数设置与实验1相同。

图5、图6分别给出了3种算法的余割平方波束和平顶波束的低副瓣方向图综合的比较结果。由图中可以看到，虽然3种方法都实现了主瓣波束的赋形，但本文方法能够得到更低副瓣电平。

表1所列为3种算法在笔形波束、余割平方波束和平顶波束的情况下得到的方向图的最高副瓣电平值。可以看到3种情况下，本文给出的IABC算法结果均优于PSO和GA的结果，能够在实现主瓣赋形的同时更好地压低副瓣电平。

表2所列为3种情况下各个算法最终收敛的适应度值。可以看到本文算法最终的搜索得到最终适应度值比PSO和GA的结果更小，因此所得到的权值矢量也更加逼近全局最优解。

图5　余割平方波束方向图

图6　平顶波束方向图

表1　3种算法副瓣电平比较

表2　3种算法的适应度值比较

从以上实验结果可以看出本文给出的算法具有较好的寻优能力，通过对权矢量空间的搜索获得最优权矢量，能够综合出逼近期望方向图的实际方向图。从收敛速度上来看，本文算法与PSO相差不大，比GA收敛速度快。从搜索精度上来看，本文算法最终收敛的适应度值在不同情况下均优于PSO和GA 2种算法，最终得到的方向图的副瓣电平高度也很好地验证了这一点。此外，PSO和GA对种群规模具有一定的要求，种群规模越大越利于寻优的结果，但这会影响算法执行效率，而IABC对种群规模并不敏感。综合来看，本文给出的IABC算法的综合效果优于PSO、GA，能够很好地实现共形阵列下的波束形成。

5　结束语

人工蜂群算法属于新兴的群智能算法，其过程简单，计算量小，易于实现，全局寻优能力强，收敛速度快。本文将人工蜂群算法应用于共形阵列天线的波束形成中，将期望方向图和实际方向图的距离作为目标函数进行优化。为了适应共形阵列下波束形成的特点，对人工蜂群算法进行了改进，通过引入多维邻域搜索策略以改善人工蜂群算法的局部搜索效率；根据期望方向图的需求，构造合适的适应度函数，通过增加罚函数来抑制副瓣电平。最终利用人工蜂群算法在权值矢量空间上搜索，得到阵列的最优权值，使获得的方向图在主瓣逼近期望方向图的同时尽可能地压低副瓣电平。实验结果表明了人工蜂群算法能够有效地实现共形阵列天线方向图的主瓣赋形和副瓣抑制。

［参考文献］

［1］Josefsson L，Persson P.Conformal array antenna theory and design［M］.John Wiley＆Sons，2006：1-46.

［2］张玉洁，龚书喜，王文涛，等.基于改进遗传算法的非规则共形阵列的研究［J］.电波科学学报，2010，25（4）：689-695.

［3］Che X Q，Bian L.Low-side-lobe pattern synthesis of array antennas by genetic algorithm［C］//4th International Conference on Wireless Communications，Networking and Mobile Computing.IEEE，2008：1-4.

［4］Khodier M M，Christodoulou C G.Linear array geometry synthesis with minimum side lobe level and null control using particle swarm optimization［J］.IEEE Transactions on Antennas and Propagation，2005，53（8）：2674-2679.

［5］Li W T，Shi X W，Hei Y Q.An improved particle swarm optimization algorithm for pattern synthesis of phased arrays［J］.Progress in Electromagnetics Research，2008，82：319-332.

［6］Quevedo-Teruel O，Rajo-Iglesias E.Ant colony optimization for array synthesis［C］//IEEE International Symposium on Antennas and Propagation Society，2006：3301-3304.

［7］Li W T，Shi X W，Hei Y Q，et al.A hybrid optimization algorithm and its application for conformal array pattern synthesis ［J］.IEEE Transactions on Antennas and Propagation，2010，58（10）：3401-3406.

［8］Bai Y，Xiao S，Liu C，et al.A hybrid IWO/PSO algorithm for pattern synthesis of conformal phased arrays［J］.IEEE Transactions on Antennas and Propagation，2013，61（4）：2328-2332.

［9］Karimzadeh-Baee R，Forooraghi K，Chamaani S.Conformal array pattern synthesis using a hybrid WARP/2LB-MOPSO algorithm［J］.International Journal of Antennas and Propagation，2012：1-7.

［10］Seong C M，Kang M，Lee C S，et al.Conformal array pattern synthesis on a curved surface with quadratic function using adaptive genetic algorithm［C］//IEEE Asia-Pacific Microwave Conference Proceedings（APMC），2013：167-169.

［11］Li W，Hei Y，Yang J，et al.Optimisation of non-uniform time-modulated conformal arrays using an improved non-dominated sorting genetic-II algorithm［J］.IET Microwaves，Antennas＆Propagation，2014，8（4）：287-294.

［12］Karaboga D.An idea based on honey bee swarm for numerical optimization，Technical report-tr06［R］.Erciyes University，Engineering Faculty，Computer Engineering Department，2005.

［13］Marinaki M，Marinakis Y，Zopounidis C.Honey bees mating optimization algorithm for financial classification problems［J］.Applied Soft Computing，2010，10（3）：806-812.

［14］Dereli T，Das G S.A hybrid‘bee（s）algorithm’for solving container loading problems［J］.Applied Soft Computing，2011，11（2）：2854-2862.

［15］孟妍，吴小瑛.人工蜂群算法综述［J］.信息技术与信息化，2013（4）：46-48.

［16］Mandal D，Bhattacharjee A K.Synthesis of cosec2pattern of circular array antenna using genetic algorithm［C］//IEEE International Conference on Communications，Devices and Intelligent Systems（CODIS），2012：546-548.

［17］Yang S，Liu C，Zheng L，et al.A study on 4D antenna arrays conformed to a cylindrical platform［C］//2013 7th European Conference on Antennas and Propagation（EuCAP）.IEEE，2013：129-131.

（责任编辑张镅）

Conformal array beamforming based on improved artificial bee colony algorithm

LIU Chao，FAN Liang-hui
（School of Computer and Information，Hefei University of Technology，Hefei 230009，China）

Abstract：The beamforming problem of conformal array with the main lobe constraint is studied，and a low sidelobe pattern synthesis algorithm based on the improved artificial bee colony algorithm（IABC）is proposed.First，the problem is formulated as an optimization problem to minimize the distance from the obtained pattern to the desired one.The multi-dimensional neighborhood search strategy is introduced to improve the local search efficiency in the weight vector space，and a penalty function is adopted to suppress the sidelobe level.With the optimal weight vector，the beam pattern can finally approach the desired one.The experimental results show that the proposed algorithm can well realize the main lobe shaping as well as the low sidelobe level，and it has a fast convergence speed.This study offers a valuable reference for the beamforming of conformal array.

Key words：conformal array；beamforming；main lobe shaping；artificial bee colony algorithm；multi-dimensional neighborhood search

作者简介：刘超（1981-），男，湖北荆州人，博士，合肥工业大学讲师，硕士生导师.

基金项目：安徽省自然科学基金资助项目（1208085QF105）；合肥工业大学博士后基金资助项目（20100480680）

收稿日期：2014-12-11；修回日期：2015-01-06

Doi：10.3969/j.issn.1003-5060.2016.01.020

中图分类号：TN821.91

文献标识码：A

文章编号：1003-5060（2016）01-0103-06