应用特征基函数法和增强间隙源模型分析阵列天线的电磁辐射特性

张锦军，杜　平，2，赵泽方（.合肥工业大学电子科学与应用物理学院，安徽合肥　230009；2.东南大学毫米波国家重点实验室，江苏南京　20096）



应用特征基函数法和增强间隙源模型分析阵列天线的电磁辐射特性

张锦军1，杜平1，2，赵泽方1
（1.合肥工业大学电子科学与应用物理学院，安徽合肥230009；2.东南大学毫米波国家重点实验室，江苏南京210096）

摘要：文章采用增强间隙源和特征基函数法（characteristic basis function method，CBFM）分析周期天线阵列的辐射方向图和输入阻抗。与传统间隙源模型相比，增强间隙源模型可克服不稳定性问题。为了测试所提方法的准确性，采用2个数值算例进行验证。数值结果表明，采用增强间隙源模型所得的结果是稳定的，采用CBFM提高了计算效率，并节约了计算资源。

关键词：增强间隙源；特征基函数法；矩量法；辐射方向图；天线阵列

杜平（1979-），男，安徽合肥人，博士，合肥工业大学副教授，硕士生导师.

0　引　言

矩量法（method of moments，MoM）已经在电磁散射与辐射问题的数值计算中得到了广泛的应用。但其产生的矩阵为稠密矩阵，内存占用多。为了解决这一问题，研究者们先后对传统矩量法做了改进，提出多层快速多极子方法（multilevel fast multipole algorithm，MLFMM）［1］、自适应积分法（adaptive integral mothod，AIM）［2］和特征基函数法（characteristic basis function method，CBFM）［3-4］等。CBFM通过将所分析的问题分块来降低矩阵的大小，从而降低了内存需求，同时也减少了CPU时间，是求解电大尺寸散射问题的一种新方法。

用矩量法分析天线时馈电方式［5-6］有传统间隙源模型、同轴线模型、微带线模型以及磁滞电压发生器模型等，它们适用于不同的天线结构。由于传统间隙源模型较为粗糙，所得结果精度不高且稳定性不好。文献［5］提出了一种增强间隙源模型，与传统馈电模型相比，该新模型具有一定的优势。比如馈电间隙电场采用脉冲函数，因此间隙处的表面电流连续，间隙内所有RWG（Rao-Wilton-Gisson）边元［7］均可作为馈电边。该模型既适用于带状馈电间隙，又可用于实心天线结构的馈电间隙。

本文采用CBFM分析平面周期阵列天线，激励源采用增强间隙源模型。

1　特征基函数法

应用矩量法分析电磁辐射问题以理想金属导体（perfect electronic conductor，PEC）电场积分方程为例，处理的矩阵方程［7］如下：

其中，Z为N×N维的阻抗矩阵；I为要求的N×1维的电流向量；V为激励电压源向量；N为未知量的个数。

首先CBFM将分析问题的区域离散成M个子域，然后通过在各个特定子域上构造一系列基函数。特征基函数由本域自作用的“一次基函数”（primary basis functions，PCBF）、域间互作用的“二次基函数”（secondary basis functions，SCBF）以及更高阶SCBF组成［8-10］。

经过CBFM的分析，方程（1）被降阶［10］为：

其中

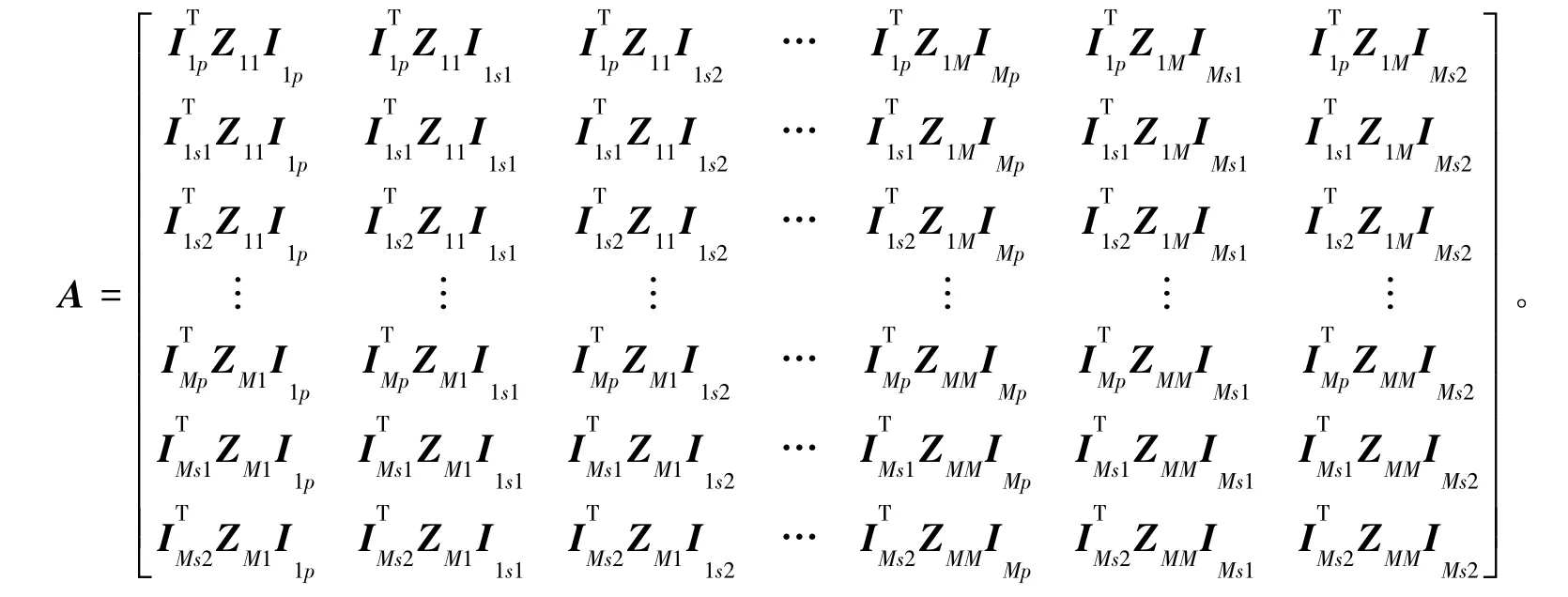
故最终表面感应电流可表示为：

由以上分析可知，采用CBFM后，矩阵的维数由N变为3M，3M远小于N，故极大降低了内存占用，同时矩阵求解的计算时间也进一步减少。

2　增强间隙源模型

本文窄带天线的激励源采用增强间隙源模型，其模型如图1所示。

图1　窄带天线的网格剖分图

对于RWG基函数，表面电流可以表示为：

其中，In和fn分别为RWG边元对应的相关系数和RWG基函数；N为三角剖分后得到的边元个数。

假如电流沿着Z轴穿过RWG边元作为馈电电流，则最简单的馈电边模型（近似为δ函数）可以表示为：

本文采用的电场是脉冲基函数的入射场激励。新得到的增强型源模型入射场激励［5，11］为：其中，zc＋和zc-分别为三角形Tm＋和Tm

-的中心轴方向和ρ分别为三角形和的非公共边对应点到三角形中心的矢量和分别为三角形和的面积；lm为第m条边边长；W为带内间隙的长度；u为阶跃函数。

增强间隙源模型的馈电电流可从任何一个馈电边元激励［5］得到，该激励的表达式为：

相应地，输入阻抗的表达式为：

其中，Is和Vs为对应的馈电电流和馈电电压。

3　数值算例

为了验证本文方法的可行性，分析2个平面周期阵列天线的辐射方向图，并比较输入阻抗的大小。计算环境为2.53 GHz Intel Core i3 CPU，4 GB内存。

算例1 1×8的阵列天线。采用图1所示的单个窄带天线，带长为λ/2，带宽为0.05 m，带内间隙长度为0.012 5 m，频率为75 MHz，天线与天线的间隔为λ/2。网格剖分产生了1 312个三角贴片时，产生了1 304条公共边。采用传统MoM求解时，要对大小为1 312×1 312的阻抗矩阵Z求逆。而采用CBFM时，最后生成的缩减矩阵A 为24×24，使得求解规模极大地降低。2种方法计算的辐射方向图如图2所示，从图2可以看出，采用CBFM或MoM结合增强间隙源计算辐射方向图在XOZ和YOZ平面的结果总体吻合良好。

图2　1×8阵列不同平面的辐射方向图

算例2 3×3的阵列天线。采用图1所示的单个窄带天线，带长为λ/2，带宽为0.05 m，带内间隙长度为0.012 5 m，频率为75 MHz，单元间隔为λ/2。网格剖分产生了1 476个三角贴片时，产生了1 467条公共边。采用传统MoM求解时，要对大小为1 467×1 467的阻抗矩阵Z求逆。而采用CBFM时，最后生成的缩减矩阵A为27×27，使得求解规模极大地降低。

2种方法计算的辐射方向图如图3所示，从图3可以看出，采用CBFM或MoM结合增强间隙源计算的辐射方向图在XOZ平面和YOZ平面结果吻合良好。

图3　3×3阵列不同平面的辐射方向图

MoM和CBFM分析的计算时间见表1所列，由表1可以看出，在相同剖分精度下，CBFM比MoM需要的时间少，单元越复杂，节省的时间越多，同时内存占用相对越少。

表1　MoM与CBFM计算时间的比较　s

对应天线阵列的输入阻抗见表2所列。表2中（i，j）表示第i行第j列天线单元。由表2可以看出，2种方法所得的输入阻抗吻合较好。实部变化很小，误差主要来源于虚部，采用增强间隙源模型求得的输入阻抗虚部比较稳定。

表2　不同天线阵列输入阻抗

4　结束语

本文采用基于区域分解思想的CBFM，结合增强间隙源模型方法分析平面周期天线阵列的辐射方向图和输入阻抗，其结果的精度、稳定性以及效率已用数值算例进行验证。结果表明，增强间隙源模型能够与CBFM结合分析平面周期天线阵列。本文仅分析了平面的周期阵列，用该方法分析媒质中的天线阵列特性将是进一步研究的重点。

［参考文献］

［1］Song J M，Lu C C，Chew W C.Multilevel fast multipole algorithm for electromagnetic scattering by large complex objects ［J］.IEEE Transactions on Antennas and Propagation，1997，45 （10）：1488-1493.

［2］Bleszynski E，Bleszynski M，Jaroszweicz T.AIM：adaptive integral method for solving large-scale electromagnetic scattering and radiation problems［J］.Radio Science，1996，31（5）：1225 -1251.

［3］Prakashs V S，Mittra R.Characteristic basis function method：a new technique for efficient solution of method of moments matrix equations［J］.Microwave and Optical Technology Letters，2003，36（2）：95-100.

［4］Yeo J，Koksoy S，Prakash V V S，et al.Efficient generation of method of moments matrices using the characteristic function method［J］.IEEE Transactions on Antennas and Propagation，2004，52（12）：3405-3410.

［5］Ding W，Liang F，Yuan B.An enhanced gap source model［J］.IEEE Transactions on Antennas and Propagation，2013，61 （3）：1266-1272.

［6］Makarov S.MoM antenna simulations with Matlab：RWG basis functions［J］.Antennas and Propagation Magazine，2001，43 （5）：100-107.

［7］Rao S M，Wilton D R，Glisson A W.Electromagnetic scattering by surfaces of arbitrary shape［J］.IEEE Transactions on Antennas and Propagation，1982，30（3）：409-418.

［8］胡怀宏，孙玉发.一种快速计算阻抗矩阵的有效方法［J］.合肥工业大学学报：自然科学版，2011，34（4）：617-619.

［9］聂在平，徐利明.电磁散射数值分析的特征基函数方法［J］.电波科学学报，2004，19（Z1）：45-49.

［10］Sun Y F，Chan C H，Mittra R，et al.Characteristic basis function method for solving large problems arising in dense medium scattering［C］//IEEE Antennas and Propagation Society International Symposium，Vol 2，2003：1068-1071.

（责任编辑闫杏丽）

Analysis of electromagnetic radiation characteristics of antenna array by using CBFM and enhanced gap source model

ZHANG Jin-jun1，DU Ping1，2，ZHAO Ze-fang1
（1.School of Electronic Science and Applied Physics，Hefei University of Technology，Hefei 230009，China；2.State Key Laboratory of Millimeter Waves，Southeast University，Nanjing 210096，China）

Abstract：In this paper，the characteristic basis function method（CBFM）and the enhanced gap source model are utilized to analyze the radiation pattern and the input impedance of the periodic antenna arrays.Comparing with the conventional gap source model，the enhanced gap source model can overcome the instability.To test the validity of the proposed method，two numerical examples are simulated.It is shown that the results obtained by the enhanced gap source model are stable.Meanwhile，the CBFM can improve the computation efficiency and reduce the memory requirement.

Key words：enhanced gap source；characteristic basis function method（CBFM）；method of moments（MoM）；radiation pattern；antenna array

作者简介：张锦军（1990-），男，湖北黄冈人，合肥工业大学硕士生；

基金项目：高等学校博士学科点专项科研基金资助项目（20130111120025）；国家重点实验室开放课题资助项目（K201507）

收稿日期：2014-12-08；修回日期：2015-02-05

Doi：10.3969/j.issn.1003-5060.2016.01.019

中图分类号：TN011.4

文献标识码：A

文章编号：1003-5060（2016）01-0099-04