基于数据驱动的PID自整定方法的研究

房　耀，董学平，张薛礼（合肥工业大学电气与自动化工程学院，安徽合肥　230009）



基于数据驱动的PID自整定方法的研究

房耀，董学平，张薛礼
（合肥工业大学电气与自动化工程学院，安徽合肥230009）

摘要：传统的PID参数整定依赖于数学模型，通过大量工程实验来确定，这给PID的实际应用带来很大的局限性。文章基于数据驱动理论，提出一种PID参数在线自整定方法，适用于非线性离散系统，该方法无需系统模型的相关信息，且具有PID方法的适应性、抗干扰性、可靠性。通过仿真比较试验结果，验证了这种自适应数据驱动PID参数整定算法的可行性和有效性。

关键词：数据驱动控制；自适应控制；非线性离散系统；PID自整定

董学平（1962-），男，安徽舒城人，博士，合肥工业大学副教授，硕士生导师.

0　引　言

PID是工业过程控制中应用最广泛的控制器之一［1］，而传统的PID控制器很难实现对复杂模型的高精度控制［2］。自适应PID算法通过自动辨识被控过程参数，自动整定控制器参数来适应被控系统参数的变化，从而实现对复杂系统的精确控制。自适应PID算法根据参数设计的原理，可大致分为极点配置自适应、相消原理自适应、基于二次型指标的自适应、神经网络自适应、模糊PID自适应［3］。其中，极点配置自适应算法只适用于二阶及二阶以下系统，控制效果的好坏和极点配置的好坏有很大关系；相消原理自适应对系统模型有较高的要求，限制了策略的使用范围；基于二次型指标的自适应，适用于最小相位系统，很难大规模应用；神经网络虽然能够实现PID的最优控制，但是结构和算法都比较复杂；模糊PID算法的模糊化过程和反模糊过程缺乏科学有效的方法，主要靠经验和试凑，限制了算法在实际工程中的应用［2-4］。

数据驱动算法不需要被控系统的模型，只根据系统的输入输出设计控制器［5-6］。然而算法的鲁棒性是建立在基于模型的条件下，对于数据驱动控制器来说，其鲁棒性的说法和定义都是不严谨的[7]。

本文提出的基于数据驱动控制的PID在线自整定策略，用于可控的非线性离散系统中，利用在线和离线的输入输出数据，使算法可以摆脱控制器对模型的依赖，可实现参数的在线自整定。此策略能简单地确定PID 3个参数，且具有快速性和抗干扰性，效果优于常规的增量式PID算法。

1　控制器设计及参数整定算法

1.1问题描述

对非线性SISO数学模型的描述如下：其中，u（k）∈R，y（k）∈R，分别表示k时刻系统的输入和输出；ny、nu为2个未知的正整数；f（…）：Rny＋nu＋2|→R为未知的非线性函数。为此对系统（1）式提出一些假设。

假设1系统（1）式是输入输出可观测的、可控制的，这是对系统可控的最基本要求。

假设2系统（1）式除有限时刻外，f（…）关于第（ny＋2）个变量的偏导数是连续的。

假设3系统（1）式满足广义Lipschitz的条件，即对任意的k1≠k2，k1，k2≥0和u（k1）≠u（k2）有：

其中，y（ki＋1）＝f（y（ki），…，y（ki-ny），u（ki），…，u（ki-nu）），i＝1，2；b＞0是一个常数。

引理1当非线性系统（1）式满足假设1～假设3，对所有时刻k有Δu（k）≠0成立时，一定存在伪偏导数φ（k），使得：

且|φ（k）|≤b，其中b为一个正常数［8］。

1.2数据驱动控制算法和收敛性分析

设计一个控制器，使得控制器输出跟上系统期望输出，即

根据“使u（k）最优”设计如下的目标函数：

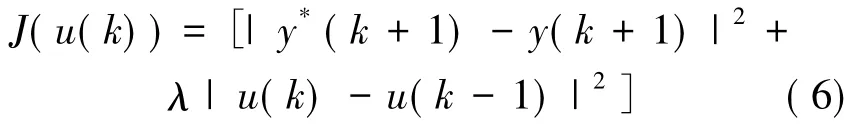
其中，λ＞0为一个权重因子；y*（k＋1）为期望的输出信号。

将（5）式代入（6）式，对u（k）求偏导，并等于0，可得如下控制算法：

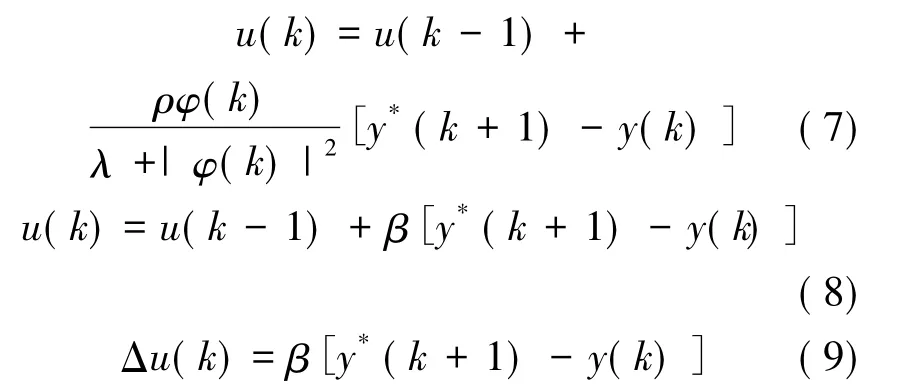
其中，ρ∈（0，1］为步长因子；β＝ρφ（k）/（λ＋|φ（k）|2）为控制器的一个设计参数。由此只需要求出φ（k），便可以求出系统的设计参数。

由于φ（k）为时变参数，需要根据被控对象的I/O数据来求最优解：

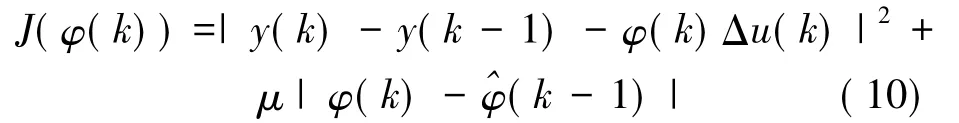
其中，μ＞0为权重因子；^φ（k-1）为上一时刻的估计值。

对（10）式求关于φ（k）的极值，可得：其中，η∈（0，1］为加入的步长因子。

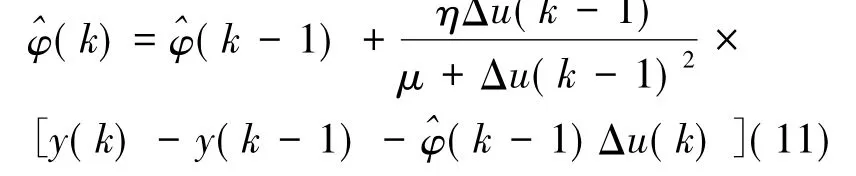
算法中λ用来限制输入量的变化Δu（k），在控制系统中被用来保证控制输入信号具有一定的平滑性；适当选取λ可保证被控系统的稳定性并获取较好的输出性能，且能有效避免控制律中的分母为0的情况；ρ、η使算法更具一般性，一般取值接近1，可获得较好的曲线；μ为对φc（k）估计值的惩罚因子［8］。

假设4对任意时刻k和Δu（k）≠0，系统伪偏导数的符号保持不变，满足φ（k）＞ε＞0或φ（k）＜-ε＜0，其中ε为一个小正数。

引理2针对非线性系统（1）式，在假设1～假设4的前提下，有系统输出跟踪误差是单调收敛的，且|y*-y（k＋1）|＝0［8］。

1.3控制器参数自整定算法

增量式PID的表达式为：

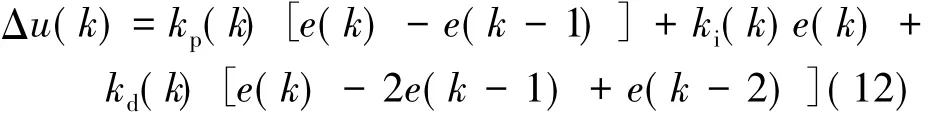
其中，kp（k）、ki（k）、kd（k）为k时刻的PID参数。使（12）式与（9）式相等，则有：

为此，假定任意3个连续的采样时刻k-2、k-1、k 的PID参数固定不变，则有：

得到（14）～（16）式的三元一次方程组，即

简写为：

其中

结论1（18）式中矩阵A，若rank（A）＝3，则方程组必然存在唯一解P＝（A）-1b，就是新的PID参数，而且使得系统能够跟上期望输出。

结论2若rank（A）＜3，则系统可能解不存在或者多解。此时不更新PID值，依旧使用上一时刻的PID值。

如此便实现了PID参数的在线自整定。由引理2可知，给定一个有界的输入u（k）可以得到有界的输出y（k），且能够跟上系统期望输出，则此算法是收敛的。

1.4控制器设计的实现步骤

（2）系统初始条件，u（1）＝u（2）＝0；y（1）＝y（2）＝0；e（k-4）＝e（k-3）＝0。

（3）利用（9）式、（11）式和e（k - 2）＝u（k-1）＋Δu（k）-y（k），求出e（k-2），同理求出e（k-1）。

（4）利用步骤（3）中公式同理求出e（k）。求出A矩阵和b矩阵，若rank（A）＝3，则PID参数矩阵P＝（A）-1b。若rank（A）＜3，则不更新PID参数矩阵；

（5）对步骤（4）进行迭代，更新PID控制器参数。

2　仿真研究

着重对本文提出的基于数据驱动的PID自整定方法进行仿真研究，仿真研究包含2个部分内容：

（1）本文方法的有效性和收敛性研究。

（2）本文方法和增量式PID比较性研究。

这些仿真研究从理论上证明了本算法的优越性和收敛性。

2.1理论证明算法的收敛性和优越性

非线性系统为：

y（i）＝0.8y（i-1）-0.5y（i-2）＋0.5u（i-1），其中i为正整数。

系统的期望输出为：

则系统仿真图如图1所示，可以看出，基于数据驱动的PID自整定能够在有限的时间内完成收敛，并能跟踪上系统的期望输出，且不会出现较大的超调，能得到比较满意的控制效果。其中步长因子ρ＝0.98，η＝0.88；仿真权重λ＝0.97，μ＝0.1。

图1　系统的有效性验证图

2.2本方法与增量式PID方法的对比图

同样，非线性系统为：

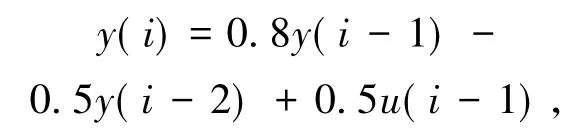
其中，i为正整数。在仿真步骤为170时加入幅值为0.1、持续一个采样间隔的干扰脉冲，系统的期望输出为：

则本方法与增量式PID的比较仿真图如图2所示，自整定算法3个参数变化规律如图3所示。

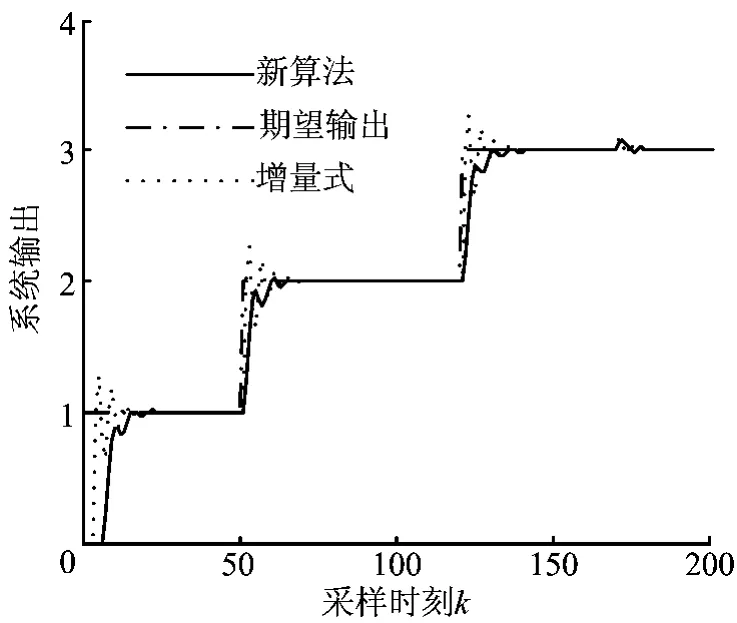
图2　本方法与增量式PID方法的比较仿真结果

图3　自整定PID的参数变化

可以看出本方法的系统跟踪速度比增量式PID更快（误差在5%内认为跟上）。当期望输出变化时，自整定系统跟踪偏差较大，PID 3个参数迅速变化，保证了跟踪曲线的快速性和平滑性；系统跟踪偏差变小，kp、kd相应变化，ki减小并趋于0；最终系统进入稳态时，PID 3个参数保持不变。由于快速性和超调是一对不可调和的矛盾，所以只能保证快速性的同时，尽量保证跟踪曲线不超调。当加入干扰，系统输出紧跟期望输出，PID 3个参数略微调整重新进入稳态。控制器不用通过大量工程整定试验便能得到系统的PID参数，算法和结构简单，可通过系统本身的自学习、自整定，可以有效地解决PID参数难以确定的缺点，并具有一定的抗干扰能力。其中增量式PID的3个参数kp＝0.7，ki＝1.15，kd＝0.2。

3　结束语

本文提出的一种基于数据驱动的PID在线自整定控制策略，其基本思路就是利用系统的期望输入输出计算出此时PID的最优解。此方法有如下优点：①系统响应速度较快；②系统参数整定简单；③系统具有抗干扰性；④系统对于模型的非依赖性。除此之外，本算法不需要通过大量的整定试验来确定PID参数，只需要系统通过自身调整。特别对于复杂系统，当系统参数发生变化导致系统模型变化时，普通的PID很难通过抗干扰性来跟踪系统的输出，而本方法可动态调整PID参数来达到控制系统的设计要求。

［参考文献］

［1］黄友锐，曲立国.PID控制器参数整定与实现［M］.北京：科学出版社，2010：6-100.

［2］孟祥泉.PID自整定方法与控制器研制［D］.大连：大连理工大学，2010.

［3］赵国山，仇性启.自适应PID的发展概况［J］.化工自动化及仪表，2006，3（38）：1-5.

［4］葛锁良，杨旭玮，张亚东.RBF网络自整定PID控制在网络化控制系统中的应用［J］.合肥工业大学学报：自然科学版，2011，34（10）：1489-1491，1550.

［5］王卫红，侯忠生，霍海波.基于数据驱动方法的控制器设计及其参数整定［J］.系统科学与数学，2010，30（6）：792-805.

［6］Leandro S C，Marcelo W P，Sumar R R，et al.Model-free adaptive control design using evolutionary-neural compensator［J］.Expert Systems with Applications，2010，37（1）：499-508.

［7］侯忠生，许建新.数据驱动控制理论及方法的回顾和展望［J］.自动化学报，2009，35（6）：650-667.

［8］侯忠生，金尚泰.无模型自适应控制：理论与应用［M］.北京：科学出版社，2013：23-150.

（责任编辑马国锋）

Research on PID parameter self-tuning based on data-driven control

FANG Yao，DONG Xue-ping，ZHANG Xue-li

（School of Electric Engineering and Automation，Hefei University of Technology，Hefei 230009，China）

Abstract：The traditional PID parameter tuning depends on mathematical model，but also needs a large number of engineering experiments to ensure parameter，which has limited the practical application of PID severely.In this paper，an online PID parameter self-tuning method is proposed based on data-driven control，which has the advantages of strong adaptability，anti-interference，and reliability，and can solve the problem of the dependence of model and realize the online PID parameter self-tuning in discrete nonlinear system.And the feasibility and effectiveness of the proposed PID parameter self-tuning algorithm based on data-driven control are verified by comparative simulation tests.

Key words：data-driven control；adaptive control；discrete nonlinear system；PID self-tuning

作者简介：房耀（1990-），男，安徽亳州人，合肥工业大学硕士生；

基金项目：合肥工业大学产学研校企合作资助项目（H-037）

收稿日期：2014-12-29；修回日期：2015-04-07

Doi：10.3969/j.issn.1003-5060.2016.01.009

中图分类号：TP 273.2

文献标识码：A

文章编号：1003-5060（2016）01-0046-04