混合整数规划性质及其构造的超加性函数

杨孝斌

(凯里学院 数学科学学院， 贵州 凯里 556011)



混合整数规划性质及其构造的超加性函数

杨孝斌

(凯里学院 数学科学学院， 贵州 凯里 556011)

摘要：针对混合整数规划的一般性案例，给出其对应的线性松弛规划表达.用3个具体案例来解读有效不等式在整数规划问题中的使用，引出Gomory整数割平面.构造超加性函数并探寻它和混合整数规划割平面的关系.分析结果表明：当超加性函数中的参数取值不同时，可以获得Gomory整数割平面、混合整数规划的取整割平面及混合整数规划的整数割平面.

关键词：混合整数规划； 超加性函数； 割平面； 线性松弛规划

在整数规划松弛中求解有效不等式，往往可以将那些非整数最优解排除，并且将整数最优解保留下来[1-3].这个区分非整数最优解和整数最优解的位置，称为“割平面”，获得“割平面”的处理也被称之为“取整”[4-6].大量的研究成果证实，“取整”操作是可以在有限次的运算步骤之后获得有效不等式[7-11].在整数割平面的理论基础之上，小数割平面理论也得以建立[12].相关的证明表明：如果获得小数割平面的方法得当，可以通过有限收敛获得小数割平面.通过整数割平面理论和小数割平面理论的结合，混合整数割平面理论也得以建，混合整数割平面的有限次收敛特性也被证实[13].在混合整数规划问题中，获取混合整数集合的有效不等式是一类重要问题，超加性函数是可以获取此类有效不等式的重要方法之一[14-15].本文针对混合整数规划问题展开研究，深入分析混合整数规划的性质，并探寻获取混合整数规划有效不等式的超加性函数方法，进而研究超加性函数中几类割平面的关系.

1混合整数规划的性质

混合整数规划问题为

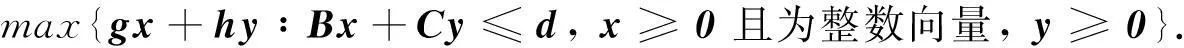
(1)

线性松弛规划问题为

(2)

线性松弛规划问题对应的约束条件形成的凸集为

(3)

式(1)对应的混合整数规划问题中约束凸包所形成的离散混合集合为

(4)

式(4)中: MIP为整数混合规划.

定义1对于混合整数规划问题，要使bx+cy≤d0成为有效不等式，则(x,y)∈QMIP.

定义2要使得bx+cy≤d0成为混合整数规划问题的割平面，必须满足Q∩{(x,y)∈Rn+p∶bx+cy≤d0⊂Q.

2实例

实例1有限容量选址问题的约束模型为

(5)

式(5)中：xi,j≥0；yj∈{0,1}.如果所有可行解都满足xi,j≤djyj，yj∈{0,1}，那么，xi,j≤min{bi,ci}yj为有效不等式.

实例2假设有多个快递公司可以解决第j个电商客户的需求bj，第i个快递公司的快递车辆数量为gi，承载能力为hi，第i个快递公司为第j个电商客户完成运输任务的费用是fi,j，相应的整数规划问题为

(6)

实例3假设一个整数规划问题的集合为

有效不等式为

对不等式左侧执行向上取整操作，即2x1+2x2+x3+x4≥6，其为QIF的有效不等式.

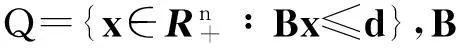
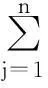
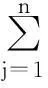
在最优单纯型表的条件下，假设该行的基变量是整数变量，同时满足最优值并不是整数.用一行约束形成割平面，以获得线形松弛问题的最优解，保留所有整数解.假设单纯型表内，行的集合表示为

(7)

设d0∉Z，满足fj=bj-[bj],fj=hj-[hj]，f0=b0-[b0]，那么，式(7)所对应的混合整数割平面为

(8)

因此，式(8)也是QMIP的有效不等式.

3超加性函数的构造及其应用

假设存在一个函数G∶Rm→R1，并且这个函数满足

1) 函数初值为G(0)=0；

2) 对于Rm域上存在的全部p,q，满足G(p)+G(q)≤G(p+q)，

则函数G称之为超加性函数.

当p≤q时，G(p)≤G(q)，超加性函数是非降的.

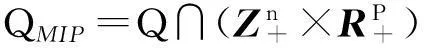
1)函数Gκ表达的也是一个超加性函数，并且这个超加性函数是非降的；

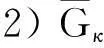
假设一个混合整数规划的线性松弛问题，其中的最优单纯型表的某一行表示为

(9)

式(9)中：N1为整数变量的非基变量的集合；N2为非整数变量的非基变量的集合.

超加性函数中的参数κ的不同取值对应不同规划的割平面.

1) 当κ为max{f,f1,…,fn}时，可以获得Gomory整数割平面；

2) 当κ=f≠0时，可以获得混合整数规划的取整割平面；

3) 当κ为min{f,f1,…,fn}时，可以获得混合整数规划的整数割平面.

参考文献：

[1]ARBOBC,MARINELLIF,VENTURAP.One-dimensionalcuttingstockwithalimitednumberofopenstacks:Boundsandsolutionsfromanewintegerlinearprogrammingmodel[J].InternationalTransactionsinOperationalResearch,2016,23(2):47-63.

[2]PAQUAYC,SCHYNSM,LIMBOURGS.Amixedintegerprogrammingformulationforthethree-dimensionalbinpackingproblemderivingfromanaircargoapplication[J].InternationalTransactionsinOperationalResearch,2016,23(2):187-213.

[3]KAYAO,UREKB.Amixedintegernonlinearprogrammingmodelandheuristicsolutionsforlocation,inventoryandpricingdecisionsinaclosedloopsupplychain[J].ComputersandOperationResearch,2016,65(8):93-103.

[4]董振宇，冯恩民，尹洪超，等.国际原油价格预测的双层随机整数规划模型、算法及应用[J].运筹学学报,2015,19(3):18-25.

[5]张甲江，高岳林，高晨阳.非线性混合整数规划问题的改进量子粒子群算法[J].太原理工大学学报,2015,46(2):196-200.

[6]庄巧莉，戴文战，王寿光.基于混合整数规划的一般Petri网死锁检测方法[J].控制理论与应用,2015,32(3):374-379.

[7]卢敬.一种求解0-1背包问题的整数混沌粒子群优化算法[J].华侨大学学报(自然科学版),2013,34(5):516-520.

[8]BEHIRYSH.Erratum:SolutionofnonlinearFredholmintegro-differentialequationsusingahybridofblockpulsefunctionsandnormalizedBernsteinpolynomials[J].JournalofComputationalandAppliedMathematics,2016,294:446.

[9]张章，汪亚明，郑俊褒，等.混沌遗传算法用于求解混合整数规划问题[J].工业控制计算机,2015,28(4):123-125.

[10]NAVICKAS Z,RAGULSKIS M.Comments on a new algorithm for automatic computation of solitary wave solutions to nonlinear partial differential equations based on the exp-function method[J].Applied Mathematics and Computation,2014,243(11):419-425.

[11]MESAROS A,HEITTOLA T,DIKMEN O,et al.Sound event detection in real life recordings using coupled matrix factorization of spectral representations and class activity annotations[C]∥IEEE International Conference on Acoustics, Speech and Signal Proceeding.Brisbane:ESTA Press,2015：151-155.

[12]李枝勇,马良,张惠珍.整数规划的量子行为蝙蝠算法[J].计算机工程与科学,2014,36(7):1336-1340.

[13]杨明歌,常水珍.求解整数规划的割平面法的研究[J].洛阳师范学院学报,2014,33(5):1-5.

[14]张小玲,李端.整数规划新进展[J].运筹学学报,2014,18(1):39-68.

[15]高海云.非线性混合整数规划的一类罚函数法[J].福州大学学报(自然科学版),2014,42(2):219-225.

(责任编辑： 陈志贤 英文审校： 黄心中)

Properties of Mixed Integer Programming and the Structured of Super Additive Function

YANG Xiaobin

(College of Mathematical Sciences, Kaili University, Kaili 556011, China)

Abstract：To the general case of mixed integer programming, and the corresponding linear relaxation programming is given. By three specific examples to interpret the effective inequality in integer programming problem, and then the Gomory integer cutting plane is introduced. Finally, we construct the super additive function and explore its relation between the cutting plane of the mixed integer programming. Results show that: when the parameters of the super additive functions are respectively chosen different, gomory integer cutting plane, mixed integer linear programming rounding cut plane, mixed integer programming integer cutting plane can be obtained.

Keywords：mixed integer programming; super additive function; cutting plane; linear relaxation programming

中图分类号：O 221.4

文献标志码：A

基金项目：贵州省教育厅优秀科技创新人才科研基金资助项目(2013153)； 凯里学院高层次人才科研启动项目(BS201309)

通信作者：杨孝斌(1979-)，男，副教授，主要从事混合整数规划和超加性函数的研究.E-mail:328880809@qq.com.

收稿日期：2015-12-22

doi:10.11830/ISSN.1000-5013.2016.02.0257

文章编号：1000-5013(2016)02-0257-04