量子Fourier变换在实现Deutsch-Jozsa算法中的应用

张洪涛, 熊红梅, 凃玲英, 舒军

(1. 湖北工业大学 纳米电子技术与微系统实验室, 湖北 武汉 430068;

2. 湖北工业大学 电气与电子工程学院, 湖北 武汉 430068)



量子Fourier变换在实现Deutsch-Jozsa算法中的应用

张洪涛1,2, 熊红梅1,2, 凃玲英1,2, 舒军2

(1. 湖北工业大学 纳米电子技术与微系统实验室, 湖北 武汉 430068;

2. 湖北工业大学 电气与电子工程学院, 湖北 武汉 430068)

摘要：提出利用量子Fourier变换解决Deutsch-Jozsa算法问题的观点.结合量子Fourier变换和Deutsch-Jozsa算法的量子电路，找到一种利用量子Fourier变换解决Deutsch-Jozsa算法新的量子电路，并考察该量子电路中各个线路的量子状态，结合算法对该量子线路的状态进行研究.结果表明：利用量子Fourier变换解决Deutsch问题，能够有效地提高运算速度，节省运算时间.

关键词：Deutsch-Jozsa算法； 量子傅里叶变换； 量子电路； 量子算法

近年来，随着量子计算机研究的发展，人们不断地探索新的实现量子计算机的方案和新的量子算法.Deutsch-Jozsa算法是由Deutsch等[1]在1992年提出的第一个量子计算算法,并由Cleve等[2]在1998年提出改进.1994年，Shor[3]构造了大数质因子分解的量子算法，Shor算法可以在多项式时间内，求解大整数分解和有限域上离散对数问题.1996年，Grover给出了一种量子搜索算法[4]，Grover量子搜索算法可以平方根地加速无序数据库的搜索.自Shor算法和Grover量子搜索算法提出以后，有研究者将量子理论原理与智能计算相结合提出了量子智能计算[5].有关Deutsch-Jozsa算法的研究也一直在继续向前，并取得相当不错的成绩.罗军等[6]在核磁共振量子计算机上实验实现了7位Deutsch-Jozsa算法;Zheng[7]利用腔QED实现了Deutsch-Jozsa算法;Dasgupta等[8]在原子系统中实现了Deutsch-Jozsa算法.量子傅里叶变换[9]作为一种基本量子工具，它在Shor的大数质因子分解算法已经得到了有效的应用,而Deutsch-Jozsa算法提出后,却鲜有人将其与量子傅里叶变换结合.因此，本文从Deutsch-Jozsa算法原理出发，把量子Fourier变换应用于Deutsch-Jozsa算法中.

1Deutsch-Jozsa算法

1.1Deutsch命题

函数f(x)∈{0,1}，要么f(x)对所有的x是常数，即f(x)为常数；要么f(x)是平衡函数，即对x的所有取值，函数取1的概率为1/2，取0的概率也为1/2.A,B两人进行数据传送，A从0到2n-1中选择一个数x，并发送给B，B利用f(x)对数x进行计算，得到结果后告诉A计算结果，A必须用最快的时间，确定B用的是常数还是平衡函数[6].

1.2Deutsch-Jozsa算法的量子线路和算法流程

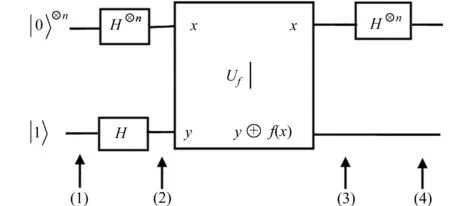
图1　实现一般Deutsch-Jozsa算法的量子线路Fig.1　Quantum circuit of the general Deutsch-Jozsa algorithm

|x,y⊕f(x)〉.

Deutsch-Jozsa算法计算过程有以下5个步骤.

步骤1状态初始化，|0〉⊗n|1〉.

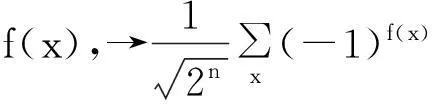
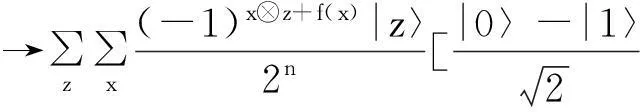
步骤5测量最终输出z，→z.

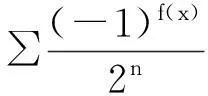
2量子Fourier变换

2.1量子Fourier变换的定义

量子Fourier变换[11]定义:在一组标准正交基|0〉,…,|N-1〉上的一个线性算子,其在基态上的作用，表示为

(1)

对任意状态的作用，可表示为

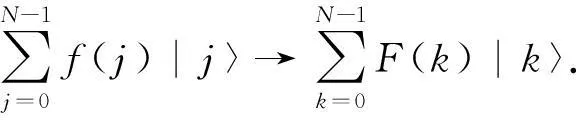
(2)

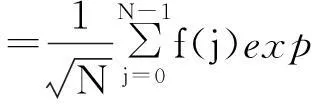
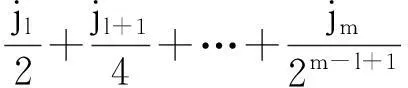
(3)

2.2量子Fourier变换的量子线路和算法流程

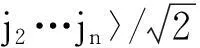
接着，对第二量子比特执行类似过程,产生状态为

对每个量子比特继续这样的操作，导出最终状态

经过交换运算，量子比特状态为

3结合量子Fourier变换的Deutsch-Jozsa算法

3.1算法的实现

在Deutsch-Jozsa算法的经典量子线路(图1)中，过多地使用了Hadamard变换,使计算比较复杂.量子Fourier变换的有效电路,如图2所示.图2中，对输入状态的每一位进行变换，得到输入状态最终的量子Fourier变换.将这两种量子线路结合，利用量子Fourier变换代替Hadamard变换，实现的方法，如图3所示.

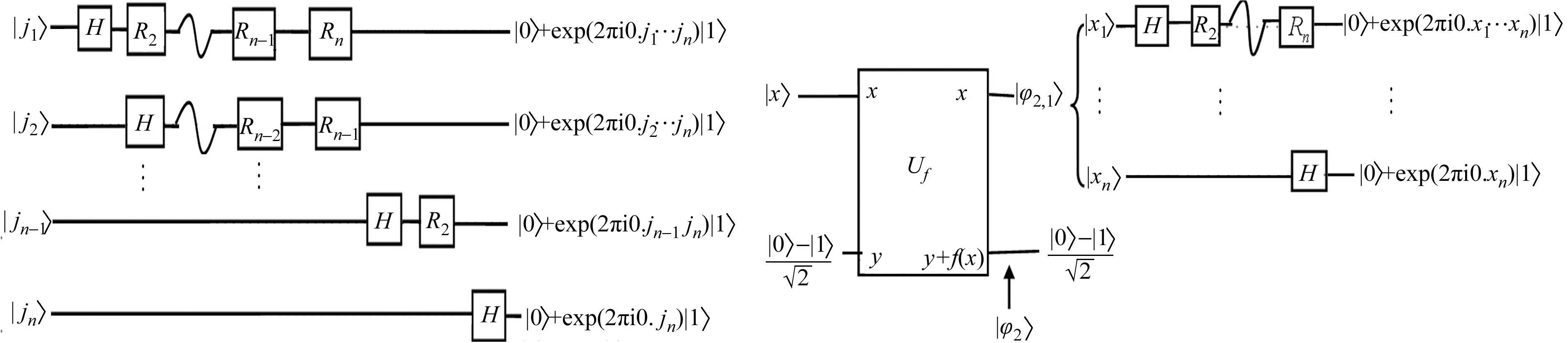
图2　量子Fourier变换的有效电路　　　　　图3　利用量子Fourier变换解决Deutsch问题的有效电路　Fig.2　Efficient circuit of quantum Fig.3　Efficient circuit of Deutsch problem 　　Fourier transform by quantum Fourier transform

3.2量子线路的分析

根据有效电路分析电路状态，初始状态为A选择的数|x〉.

B得到A发送的数|x〉后，对其使用幺正变换Uf:|x,y〉→|x,y⊕f(x)〉，可以得到|φ2〉，即

(4)

由式(4)可知：B的函数计算结果保存在量子比特的幅度中.A得到B的计算结果|φ2〉后，利用量子并行性对状态|φ21〉=(-1)f(x)|x〉进行量子Fourier变换.将状态|x〉写成二进制形式x=x12n-1+x22n-2+…+xn20.图3中，|φ2,1〉的幅值省略没有写出,即

(5)

由量子Fourier变换的定义式(2)，有

(6)

对|φ2,2〉右边部分进行交换运算，可以得到

(7)

最终，可以得到

(8)

由式(1),(3),(20)可以得到

(9)

即得到φ2,1的量子Fourier变换为

(10)

由式(10)可知：如果f(x)是常数函数，φ2，1进行量子Fourier变换后的φ2，4幅值为正数或负数；如果f(x)是平衡函数，对φ2，4的正负幅度贡献抵消，幅度为0.归纳起来，若最终测量结果是0，则函数是平衡函数；否则，函数是常数函数.

3.3算法的分析和比较

在图3的量子线路中，A直接从0到2n-1中选择的数x发送给B，B利用幺正变换Uf:|x,y〉→

|x,y⊕f(x)〉和量子并行性计算f(x)，此处的y由B提供.A得到B计算的结果后，利用量子并行性对前n位量子比特进行量子Fourier变换，再通过适当的测量，确定f(x)是平衡函数还是常数函数.

图4　两种算法的计算时间对比图Fig.4　Comparison of two kinds of algorithm in computation time

对比图1和图3可知：在Deutsch-Jozsa算法中，减少对Hadamard变换的使用，改用量子Fourier变换也一样可以快速地判断出f(x)是平衡函数还是常数函数，而且比使用Hadamard变换更简单、直接、快速.两种Deutsch-Jozsa算法的计算时间对比，如图4所示.图4中：t为时间；B为量子比特.由图4可知：同一个数x分别采用的两种Deutsch-Jozsa算法，利用量子傅里叶变换后的Deutsch-Jozsa算法比Deutsch-Jozsa算法耗时短，能更快地得到判断结果.

4结束语

文中介绍了Deutsch算法、量子线路算法和量子Fourier变换.在此基础上，推导并验证Deutsch-Jozsa算法可结合量子傅里叶变换进行快速计算，为解决Deutsch-Jozsa算法提供了新思路，这对“相对黑盒”指数加速的量子算法[12]的研究提供了新的方案，也为后面进行量子算法和量子计算机[13]的研究起着重要的作用.

参考文献：

[1]DEUTSCH D,JOZSA R.Rapid solution of problems by quantum computation[J].Proceedings:Mathematical and Physical Sciences,1992,439(1907):553-558.

[2]CLEVE R,EKERT A,MACCHIAVELLO C,et al.Quantum algorithms revisited[J].Proceedings of the Royal Society A Mathematical Physical and Enginneering Sciences,1997,454(1969):339-354.

[3]SHOR P W.Algorithms for quantum computation: Discrete logarithm factoring[C]∥Proceedings of the 35th Annual IEEE Symposium on Foundations of Computer Science.Los Alamitos:IEEE Press,1994:181-182.

[4]GROVER L.A fast quantum mechanical algorithm for database search[C]∥Proceedings of the 28th Annual ACM Symposium on the Theory of Computing.New York:ACM,1996:212-219.

[5]王蕴,黄德才,俞攸红.量子计算及量子算法研究进展[J].计算机系统应用,2011,20(6):228-231,237.

[6]魏达秀,杨晓冬,罗军,等.七量子位Deutsch-Jozsa量子算法的核磁共振实验实现[J].原子核物理评论,2002,19(2):278-280.

[7]ZHENG Shibiao.Scheme for implementing the Deutsch-Jozsa algorithm in cavity QED[J].Physical Review A,2004,70(3):034301(1-3).

[8]DASGUPTA S,BISWAS A,AGARWAL G S.Implementing Deutsch-Jozsa algorithm using light shifts and atomic ensembles [J].Physical Review A,2005,71(1):012333(1-8).

[9]NIELSON M A,CHUANG I L.Quantum computation and quantum information[M].Cambridge:Cambridge University Press,2000:32-35,217-219.

[10]BALLHYSA E.A generalization of Deutch-Jozsa algorithm[M].Germany:LAMBERT Academic Publishing,2010:15-20.

[11]付向群,鲍皖苏,王帅.ZN上离散对数量子计算算法[J].计算机学报,2014,37(5):1058-1062.

[12]龙桂鲁.量子计算算法介绍[J].物理,2010,39(12):803-809.

[13]张毅,卢凯,高颖慧.量子算法与量子衍生算法[J].计算机学报,2013,36(9):1835-1842.

(责任编辑： 黄晓楠 英文审校： 吴逢铁)

Application of the Quantum Fourier Transform in Deutsch-Jozsa Algorithm

ZHANG Hongtao1,2, XIONG Hongmei1,2,TU Lingying1,2, SHU Jun2

(1. Nanoelectron technology and microsystem Laboratory, Hubei University of Technology, Wuhan 430068, China;2. School of Electrical and Electronic Engineering, Hubei University of Technology, Wuhan 430068, China)

Abstract：A new method to solve Deutsch-Jozsa algorithm by using quantum Fourier transform was presented. Combine the quantum circuits of quantum Fourier transform and Deutsch-Jozsa algorithm, then a new quantum circuit of solving Deutsch-Jozsa algorithm used quantum Fourier transform was found. And the quantum circuit processes were observed step by step, and states of the circuit was analyzed. The results showed that solving Deutstch problem by quantum Fourier transform can improve the operation speed and save the operation time.

Keywords：Deutsch-Jozsa algorithm; quantum Fourier transform; quantum circuit; quantum algorithms

中图分类号：TP 306

文献标志码：A

基金项目：湖北省武汉市科技局“十城千辆新动力汽车计划”(2013011801010600)

通信作者：张洪涛(1963-)，男，教授，博士，主要从事数字信号处理和数字图像处理、嵌入式系统、纳米器件集成和纳米半导体技术的研究.E-mail:zhanght@mail.hbut.edu.cn.

收稿日期：2015-10-14

doi:10.11830/ISSN.1000-5013.2016.02.0155

文章编号：1000-5013(2016)02-0155-05