改进的自适应最优低秩信道估计算法

刘钰佳, 谭鸽伟

(华侨大学 信息科学与工程学院， 福建 厦门 361021)



改进的自适应最优低秩信道估计算法

刘钰佳, 谭鸽伟

(华侨大学 信息科学与工程学院， 福建 厦门 361021)

摘要：针对正交频分复用系统中线性最小均方误差(LMMSE)信道估计算法计算复杂度高，且存在当信道的统计特性与先验知识不匹配时估计性能恶化的问题，利用信道频域冲激响应的移动平均自相关函数，结合子空间分解、跟踪和序列正交原理，提出一种改进的自适应最优低秩信道估计算法.对比文中算法和LMMSE算法、LS算法和联合AIC(akaike criterion)秩估计准则的自适应低秩信道估计算法，结果表明：文中算法的秩估计更为精确；在插入导频数量较少的情况下，改进的信道估计算法能获得更高的信噪比性能增益.

关键词：正交频分复用; 信道估计; 频率选择性; 时变; 自适应; 低秩; AIC准则

由于无线通信环境中信道受到多径和多普勒频移的影响，在针对正交频分复用(orthogonal frequency division multiplexing，OFDM)系统中，接收端无法准确进行相干检测.因此，实时准确的信道估计是必要的.针对传统的信道估计中存在运算复杂度高的问题，Ozdemir等[1]提出LMMSE(linear minimum mean square error)信道估计算法，对传统MMSE(minimum mean square error)算法做了线性近似，虽然在保证了较好的性能的前提下降低了算法复杂度，但在实际运用中仍然无法实现.樊同亮[2]提出低秩(SVD)估计算法,对LMMSE算法做奇异值分解，降低了算法复杂度，但若不知道信道阶数的情况下，取随机信道阶数值则可能产生能量泄露，导致系统性能下降.石磊等[3]利用信道特性可以由信道自相关矩阵中相关性较高的元素所确定的原理，忽略其他元的作用，以此降低了运算复杂度，克服非重叠分块算法中边缘子载波处误比特率大的缺点，但是只有当信道实际阶数已知的情况下，才能获得较好的误比特率.Houda等[4]提出一种基于SVD的最优低秩信道估计，利用了循环前缀与子载波的关系，从而自适应地求出信道的阶数，该算法不需要知道信道阶数但容易遗漏某些相关信息.因此，在不知道信道阶数的情况下，就需要采取较好的方法来估计信道实际阶数.李双志等[5]提出了一种联合估计信道有效阶数和信道冲激响应的算法，引入赤池信息量准则(akaike criterion,AIC)，降低有效信道阶数估计误差，提高信道估计误比特率性能，但AIC准则对信噪比的变化很敏感.Tomasoni等[6]研究基于AIC准则的对OFDM系统信道阶数估计的算法，并利用Levinson递推算法，降低实际运算量，克服AIC准则在高信噪比时得到过估计阶数的缺点[7].本文提出一种不仅能够有效降低算法复杂度，自适应精确估计出信道阶数，并且只需插入少量导频就能获得更好性能的自适应最优低秩信道估计算法.

1OFDM系统模型

基于导频的OFDM基本模型,如图1所示.原始数据调制后，将其串并变换，插入导频符号，做IFFT(international football friendship tournament)变换信号[8]，最后，添加循环前缀CP，表达式为

(1)

信号经过信道后，表达式为

(2)

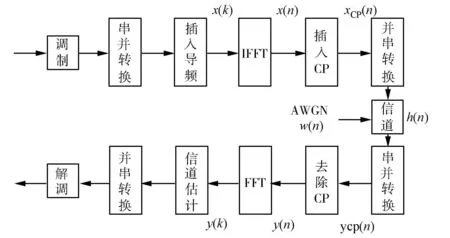
图1　基于导频的OFDM系统模型Fig.1　Model of OFDM based on pilots

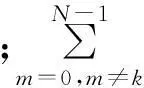
当信道为慢时变时，ICI可以忽略.

2改进的模型估计

2.1最优低秩信道估计模型

最优低秩模型利用LS(least square)算法,粗略估计出初始信道响应，结合子空间分解原理[9]降低信道自相关矩阵维数.

假设在时刻i，接收到的导频位置处的LS信道估计频域冲激响应估计值为HLS[8]，HLS的统计自相关矩阵为

(3)

式(3)中：σ2为噪声方差；IM是维数为M的单位矩.

实际信道冲激响应自相关函数为

将式(3)代入LMMSE信道估计算法，可得

(4)

由于发送信号功率归一化，且当采用QPSK调制手段时，β=1.因此，LMMSE信道估计算法可以化简成

(5)

利用特征值分解原理[10]，化简式(5)，R的表达式为

(6)

式(6)中：Us和Ud分别是信号子空间和噪声子空间；Λr是R奇异值分解得到的信号子空间对角矩阵；σ2为噪声方差；Ir为维数是r的单位矩阵.

时刻i处的最优低秩LMMSE模型为

(7)

通过化简，逆矩阵的维数大大降低了.接收端进行粗略估计时需要知道所有的导频信息，因此，传输的导频数较多时，计算量增大.为此，提出一种只需插入少量导频的方法克服其计算量随着导频数增多而增大的缺点.

2.2改进的自适应最优低秩信道估计算法

采用一次移动，接收端只需要知道估计时刻和窗口范围最后一个发送的OFDM符号的导频信息，利用移动时间平均方法估计出下一时刻的导频位置处信道频域自相关矩阵.结合序列正交迭代方法，利用改进的信号噪声空间估计法估计信号空间维数，从而实现改进的低秩信道估计算法.

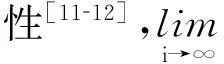
移动平均递推法的移动步长设为m，当时刻i>m时，相关矩阵为

(8)

(9)

序列正交迭代法[13]假设时间平均自相关矩阵的特征子空间矩阵为

(10)

将式(10)代入移动平均自相关矩阵,有

(11)

对A(i)做QR分解有R1(i)Q(i).当前时刻特征子空间夹角余弦值表示为

(12)

把式(12)代入式(11)，有

(13)

为了进一步降低基于移动平均法的低秩信道估计算法的误码率,对其进行修正，有

(14)

当时刻i≤m时，由于无法用一次移动平均算法，因此，采用简单时间平均算法得出的LS平均自相关函数代替瞬时统计自相关函数，得出时间平均自适应公式[11].同理，结合序列正交迭代法和QR分解可知A(i)的表达式为

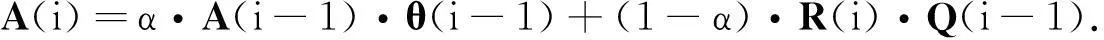
(15)

若不知道信号子空间维数或噪声子空间维数的情况下，则可以通过以下方法较精确地估计出信号子空间维数.

由奇异值分解原理，有

信号子空间的特征值对角矩阵表示为

将其代入式(10)，(12)可得

(16)

式(12)中: λk(i)为∑(i)的第k个对角元素，表示为

(17)

特征值对角矩阵表示为

(18)

式(14)中：λ1,λ2,…,λs，l为信号子空间对应的特征值；λd，1,λd，2,…,λd，M为噪声功率.

每个噪声功率不可能都相同，但集中在方差大小为λw的一定范围内，假设 λd，1=λd，2=…=λd，M=λM，信号子空间维数由下3个步骤来递归.

步骤1求出对角线上所有特征值的平均值，即信号的平均功率为

(19)

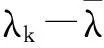
2.3算法复杂度分析

由节2.2可知：信号子空间维数精确估计为k′-1.令r1为假设的初秩估计值，一个OFDM符号内载波数为M，则可得式(15)的复杂度为M(r1)2+2Mr1，对式(19)做QR分解，复乘法的算法复杂度为2M(r1)2,最后的最优低秩算法公式的算法复杂度为3(k′-1)2+(k′-1)2.由LRA-IMP算法原理可知：在每个OFDM符号时间内，做一次信道估计.由于一次移动平均代替统计自相关值，因此，下一个OFDM符号时间内,取前面时刻保留的平均值只做一次正交迭代.将每一步运算量大小累加起来的总运算量为O(M(r1)2)，而LMMSE估计运算量约为O(M2).

3仿真结果及分析

3.1系统参数

仿真中采用的OFDM系统载波为2GHz,带宽为1MHz，由16个子载波组成，子载波间隔为62.5kHz,一个OFDM符号传输时间16μs,循环前CP占3.2μs.调制技术采用QPSK(quadraturephaseshiftkeying)，假设频率选择性信道衰落信道模型的延时功率特性为指数衰落，均方延时为3μs,信道估计结果的性能指标为20次蒙特卡罗仿真后的误比特率.

图2　改进方法的误比特率比较Fig.2　Bit error rate comparison of Improved method

3.2仿真性能与分析

无多普勒频移的条件下LMMSE信道估计算法、基于信道有效除数估计AIC准则的低秩信道估计算法(LRA-AIC)，文中的改进的自适应最优低秩(LRA-IMP)信道估计算法的误比特率(η)性能比较，如图2所示.图2中：导频间隔为140.

由图2可知：随着信噪比的增大,3种算法误比特率都呈下降趋，但LRA-IMP信道估计算法下降的趋势最快.这是因为算法较好地利用符号间的相关性，跟踪信号信息，使其估计误差降低,且在较小误差精度范围内，估计出信号子空间的维数.因此，受噪声影响相对更小.在相同误比特率条件下，改进的算法信噪比比LMMSE小，差距最大可以达约1.5 dB;与LRA-AIC信道估计算法相比，差距则最大可以达约2.5 dB.

图3　多普勒频移为10 Hz时的误比特率比较Fig.3　Bit error rate comparison when dopple is 10 Hz

多普勒频移为10 Hz的误比特率性能比较，如图3所示.由图3可知：随着信噪比的增大,LRA-IMP信道估计算法误比特率性能一直保持最好；当信噪比为20 dB以后，性能才有所下降.这是由于自适应跟踪过程中，信道的时变性受到影响，使信道间的关联性变小了；其次，在快衰落情况下也能达到较好的效果.

在不同导频间隔(15～256)下，信噪比为18 dB时，LS，LMMSE，LRA-IMP的误比特率性能比较，如图4所示.图4中：移动步(m)不同.由图4(a)可知：虽然当导频间隔(t)较小(导频数多)时，其误比特率大；但是当导频间隔大(即实际发送数据中插入导频数较少)的时候，LRA-IMP信道估计算法的误比特率保持较低水平.因此，这种改进的自适应低秩信道估计方法运用于导频数少的时候效果较好，提高了资源利用率.

由图4(b)可知:随着步长(s)的变化，其误比特率的下降趋势基本一致.因此，当硬件存储量较小,且在较短时间内信道变化明显的情况下时，可以考虑用较小的移动步长对信道进行估计;相反，当在较长时间内信道变化较慢，且不存储量较大的时候，则可以选择较大的移动步长进行信道估计.综上可知:提出算法误比特率性能不受实际存储量的限制，更有利于在不同的实际环境上实现，适用范围更大，有较好的实际运用价值.

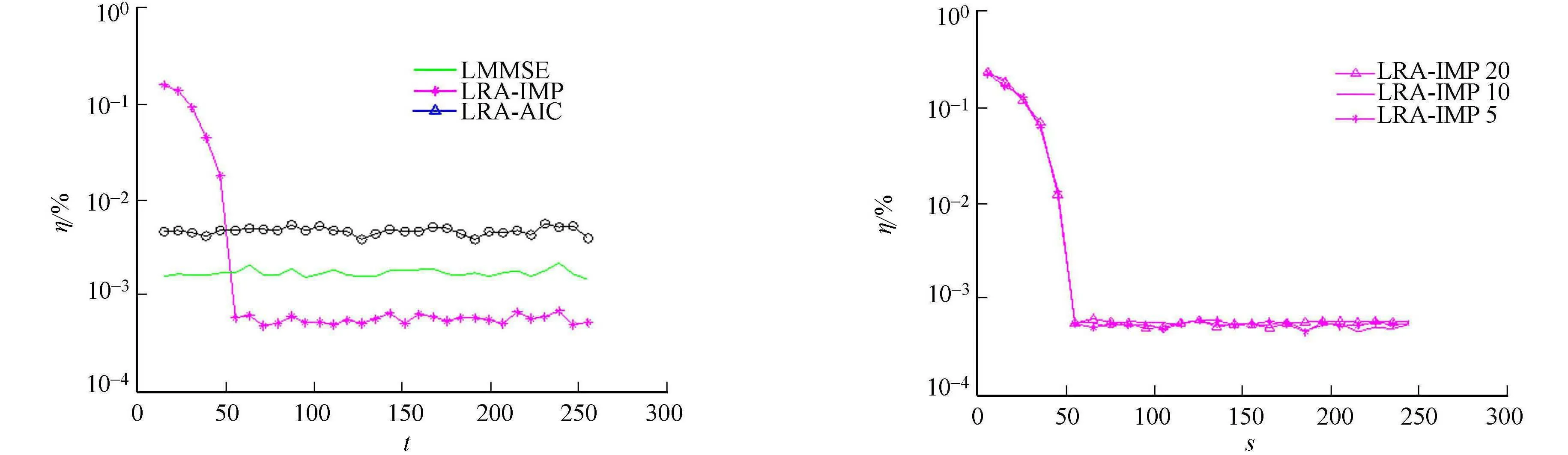
(a) 不同导频间隔 (b) 不同移动步长图4　误比特率比较Fig.4　Bit error rate comparison

4结论

首先,对OFDM的基本模型进行了分析.然后，建立了最优低秩信道估计模型，详细描述了改进算法的原理及公式推导过程，并比较了算法复杂度.最后，在不同信道条件，不同导频间隔及不同步长条件下对不同算法进行仿真比较.

综上可知,文中提出的算法无论是在信噪比较低还是较高时都可以达到较好的性能，且有利于节省收发端资源利用率.除此之外，提出的改进算法可以根据硬件要求和信道变化情况来改变移动步长，从而更好地估计发送端发送数据的信息.

参考文献：

[1]OZDEMIR M K,ARSLAN H.Channel estimation for wireless OFDM systems[J].IEEE Communication Surveys and Tutorials,2007,9(2):18-48.

[2]樊同亮.OFDM的信道估计和信号均衡技术的研究[D].重庆：重庆大学，2012:36-41.

[3]石磊,郭宝龙,李平,等.一种低复杂度LMMSE信道估计算法[J].西安电子科技大学学报(自然科学版),2012,39(2):24-28，50.

[4]HOUDA K,MALEK B,FAROUK O M.Low rank MMSE channel estimation in MIMO-OFDM systems: Innovative computing technology[C]∥Second International Conference on INTECH.Casablanca:IEEE Press,2012:279-284.

[5]李双志,张磊,张建康,等.一种新的多址信道有效阶数估计算法[J].电讯技术，2014，54(1):84-88.

[6]TOMASONI A,GATTI D,BELLINI S,et al.Efficient OFDM channel estimation via an information criterion[J].Transactions on Wireless Communications,2013,12(3):1352-1362.

[7]郭士旭,郭军利,蒋建中.一种改进的基于秩检测的信道有效阶数估计算法[J].信息工程大学学报,2012,13(5):552-557.

[8]石钧.OFDM无线通信系统信道估计及自适应算法的研究[D].北京：北京邮电大学，2012：26-28.

[9]TU Chaocheng,BENOIT C.Subspace-based blind channel estimation for MIMO-OFDM systems with reduced time averaging[J].Transactions on Vehicular Technology,2010,59(3):1539-1544.

[10]张贤达.矩阵分析与应用[M].2版.北京：清华大学出版社,2004:453-579.

[11]居敏.OFDM系统信道估计技术的研究[D].南京：南京航空航天大学,2008：26-29.

[12]RAYRA D,LOURENCO M,WILSON K,et al.Implementation aspects of adaptive window moving average filter applied to PLLs-Comparative study[C]∥Power Electronics Conference (COBEP). Brazilian: IEEE Press, 2013:730-736.

[13]PETER S.Low-rank adaptive filters[J].Transactions on Signal Processing,1996,44(12):2932-2947.

[14]STROBACH P.Bi-iteration SVD subspace tracking algorithms[J].Transactions on Signal Processing，1997,45(5):1222-1240.

(责任编辑： 陈志贤英文审校： 吴逢铁)

Improved Adaptive Optimal Low-Rank Channel Estimation Algorithm

LIU Yujia, TAN Gewei

(College of Information Science and Engineering, Huaqiao University, Xiamen 361021, China)

Abstract：Aiming at the problems of high computational complexity and estimation performance deteriorating when the statistical characteristics and prior knowledge of channel are mismatch of linear minimun mean square error channel estimation algorithm (LMMSE) in the orthogonal frequency division multiplexing system (OFDM), an improved adaptive channel estimation algorithm jointing channel rank estimation has been proposed, in which the moving-average channel correlation matrix, subspace decomposition, tracking and principle of orthogonal sequence are employed. Simulation results show that compared to different channel estimation algorithms including LMMSE, Least Sqrare channel estimation algorithm(LS), adaptive channel estimation joint akaike criterion (AIC) channel rank estimation (LRA-AIC) in frequency selective time varying channel, the proposed scheme has the best bit error rate performance and rank estimation is more accurate, and the proposed channel estimation can achieve higher RSNperformance gain under a less number of inserted pilots, thus solving the problems of high complexity of channel estimation algorithm.

Keywords：orthogonal frequency division multiplexing; channel estimation; frequency-selective; time varying; adaptive; low rank; akaike criterion

中图分类号：TN 929.5

文献标志码：A

基金项目：福建省自然科学基金资助项目(2013J01242)

通信作者：谭鸽伟(1970-)，女，讲师，博士，主要从事无线通信及SAR信号处理等的研究.E-mail:tangewei70@163.com.

收稿日期：2014-07-02

doi:10.11830/ISSN.1000-5013.2016.02.0179

文章编号：1000-5013(2016)02-0179-06