部分充填式钢箱-砼组合梁考虑滑移和剪切变形的变分解法

莫时旭， 胥海宁

(1. 广西岩土力学与工程重点实验室， 广西 桂林 541004；

2. 桂林理工大学 土木与建筑工程学院， 广西 桂林 541004)



部分充填式钢箱-砼组合梁考虑滑移和剪切变形的变分解法

莫时旭1，2， 胥海宁1

(1. 广西岩土力学与工程重点实验室， 广西 桂林 541004；

2. 桂林理工大学 土木与建筑工程学院， 广西 桂林 541004)

摘要：为研究滑移和剪切变形对部分充填式钢箱-混凝土组合梁变形影响，基于Timoshenk两广义位移理论和能量变分原理，提出组合梁变分计算模型和假定.利用最小势能原理并结合边界条件，分别推导考虑双重变形模式的简支组合钢箱梁负弯矩区滑移微分方程、挠度及附加弯矩的联合弹性解析解.对比两根不同抗剪连接程度组合梁的实测值及理论公式计算值，分析结果表明：在弹性阶段运用变分法推导的挠度及其滑移计算值与实测值相吻合，从而证明了理论公式的有效性.

关键词：部分充填式钢箱-砼组合梁； 负弯矩区； 变分法； 滑移变形； 剪切变形

部分充填式钢箱-混凝土组合梁是由钢箱梁和箱室中填充混凝土构成，通过抗剪连接键连接上混凝土翼板形成组合截面[1].近年来，对于部分充填式钢箱-混凝土组合梁的研究取得较大进展.莫时旭等[2]基于弹性抗剪理论，通过换算截面法推导出钢箱-混凝土组合梁竖向抗剪强度弹性解，分析表明填充混凝土处的竖向剪应力不可忽略.李兴科等[3-4]基于经典微段平衡方程，结合负弯矩区组合梁截面形式，推导了界面滑移微分控制方程，对比了理论值与规范值的差异性.基于能量变分原理，Schnabl等[5]考虑滑移变形及横向剪切变形对位移的影响，通过改变材料参数推导了双层组合梁受均布荷载作用下的解析解.Paoplo[6]推导考虑滑移效应下的组合梁内力计算方法，采用剪应力-滑移应变曲线对滑移变形进行了非线性分析.周勇超等[7]利用最小势能原理推导不同荷载条件滑移对组合梁附加挠度的计算方法，但并未考虑剪切变形的影响.针对该理论公式的缺陷，贺桂超等[8]结合能量变分原理，推导滑移和剪切变形双重效应下的组合箱梁弹性解析解.本文针对部分充填式钢箱-混凝土组合梁剪切变形机理，结合能量变分原理完善滑移和剪切双重作用下的受力变形机制.

1组合梁变形微分方程

1.1滑移与弯曲变形

在弹性受弯阶段，钢箱内填充混凝土和面板中的钢筋尚未屈服且套箍作用尚未显现，组合梁截面应变符合平截面假定.

采用换算截面法将下箱室填充混凝土换算为钢板，并作如下2个假定：1) 下箱室填充混凝土与腹板和中隔板粘结可靠，没有相对滑移；2) 钢箱中隔板与腹板采用焊接刚性连接，同时换算截面钢板与中隔板之间也是刚性连接.刚节点的存在会使变形受到彼此之间的限制，应力和位移边界条件更为复杂.为便于计算，假设截面保持为连续整体，忽略刚节点限制作用，使协同变形不受限制.

全截面弯曲应变可由梁的近似挠曲线微分方程表示为εb(x，y)=y·w″(x).其中：y为换算截面质点到中和轴的距离.根据轴力微分平衡方程,可得

(1)

由此解得

(2)

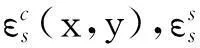
(3)

式(3)中：Sc=-nAs/(Ac+nAs)；Ss=Ac/(Ac+nAs)；n=Es/Ec.

1.2剪切变形

部分充填式钢箱-混凝土组合简支梁横截面受力前垂直于中性轴，受剪变形后的相邻横截面因剪应力沿梁宽度方向分布不均匀而产生翘曲错动[9-10]，剪力滞使组合箱梁翼缘板出现纵向位移u(x，z).同时由于中隔板和下箱室填充混凝土的影响，横截面处的翘曲位移函数和边界条件更为复杂，计算精确度受其影响较大.依据薄壁钢箱梁的计算特点，可以忽略钢箱顶底板和混凝土翼缘板对抗剪的贡献.因此，为简化计算采用以下4点假定.

1) 忽略横截面处横向应变εz和平面外剪切应变γx，z和γy，z.

2) 基于平均剪力-剪切应变本构关系，应假设剪应力沿横截面宽度方向均匀分布，使变形后的平面垂直于中性轴且只有竖向弯曲位移.

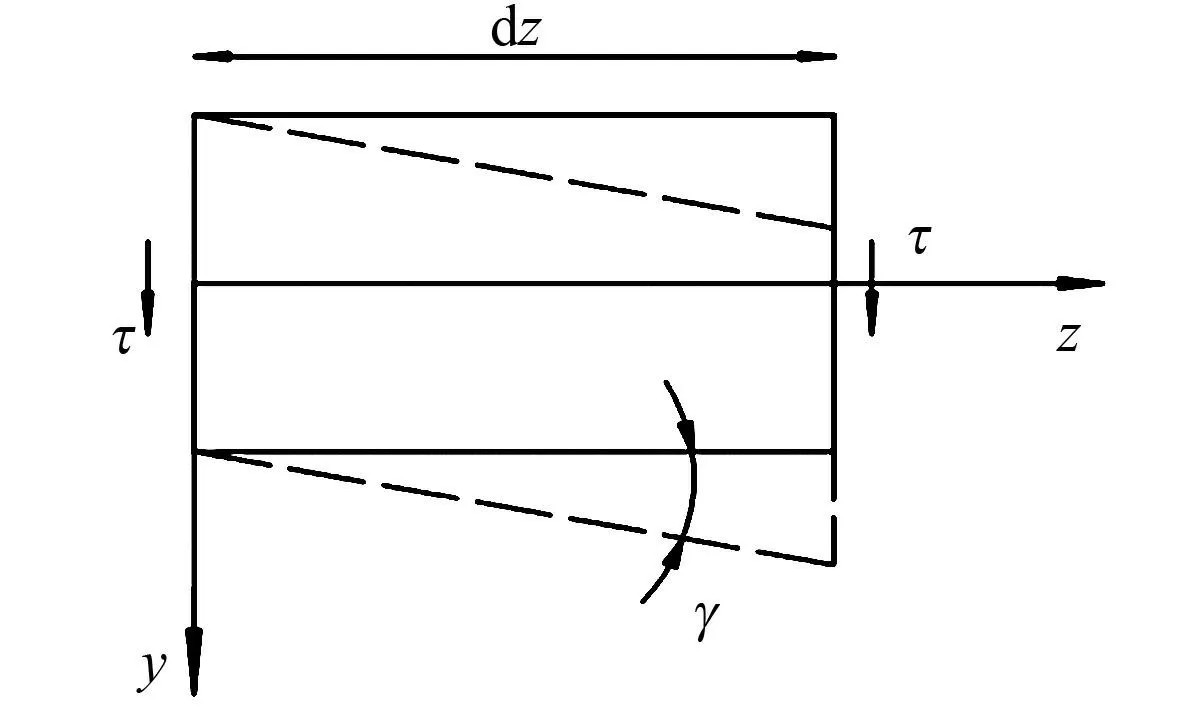
图1　剪切变形模型 Fig.1　Shear deformation model

4) 剪力对梁产生的附加挠度不会引起梁的纵向位移，可忽略剪力滞效应.

1.3组合梁计算模型

为方便利用能量变分原理推导组合梁理论公式计算值，设计了如下计算模型.假设w(x)和μ(x)分别为竖向挠度位移和组合梁相对滑移，将钢箱腹板间净距一半宽度b视为固定值，采用不同比例因子η1，η2，η3，η4，η5定义混凝土上翼板、悬臂板、钢箱顶板、中隔板、底板宽度，如图2所示.钢箱-混凝土组合梁位移滑移与剪切变形计算模式图，如图3所示.

图2　组合梁截面 图3　组合梁位移滑移与剪切变形Fig.2　Section of concrete-partial-filled　　　　　　　　Fig.3　Pattern of displacement slip　　 steel box beam　　　　　　　　　　　　　　　　　　and shear deformation

(4)

(5)

(6)

(7)

(8)

(9)

(10)

(11)

(12)

式(12)中：

Aw，Ac，At，Az，Ab，Ah分别为腹板截面积、混凝土上翼板截面积、钢箱顶板面积、钢箱中隔板截面积、钢箱底板截面积、换算截面后钢板截面积；tw，tc，tt，tz，tb，th分别为上述各截面的宽度；y1，y2分别为腹板底顶端到组合梁中和轴的距离；Ks为组合梁界面抗滑移刚度；K为无量纲的剪应力分布不均匀系数，与组合梁截面形式有关.根据最小势能原理，可得

通过分部积分，可得到如下考虑剪切变形的钢箱-混凝土组合梁挠度与滑移的基本微分方程及其边界条件，即

(14)

将式(14)中第三项代入其第一、二项，可得到曲率一阶导数方程和组合梁相对滑移微分方程分别为

(15)

(16)

对式(15)积分一次，曲率方程为

(17)

式(17)中:Mf=E3I3μ′(x)；M(x)，Mf(x)分别为初等梁弯矩和考虑滑移剪切效应的附加弯矩，将两者之和代入式(17)，即为组合梁截面弯曲曲率.

2控制微分方程的求解

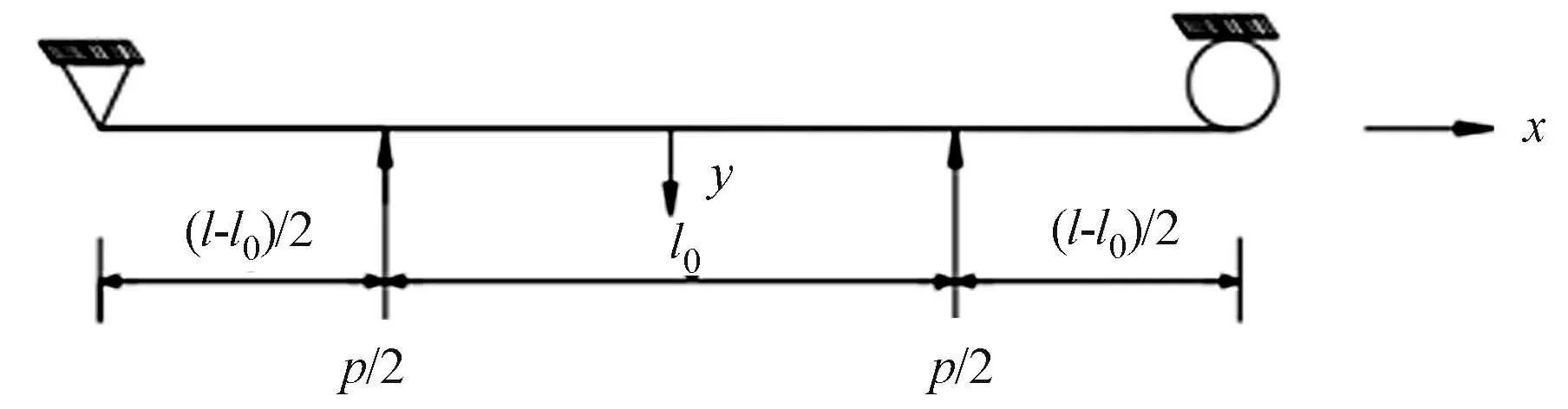
图4　组合梁加载模式图Fig.4　Loading setup of beam

μ1(x)=C1chm1x+C2shm1x，

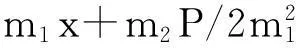
由此，可得到参数为

由此，可最后得到负弯矩区部分充填式钢箱-混凝土组合梁考虑滑移与剪切变形的纯弯段和剪弯段的相对滑移方程，分别为

(18)

(19)

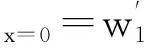
(20)

(21)

由此，可得到跨中挠度为

(22)

对比于经典梁跨中挠度，其第一项为初等梁理论中不考虑剪切变形的挠度，第二项为考虑滑移和剪切变形的附加弯矩挠度修正项.

3计算值论证

采用反向加载方式模拟组合梁负弯矩区受力，设计抗剪连接度为1.00和0.75的部分充填式钢箱-混凝土组合简支梁对比试件，验证负弯矩区考虑滑移和剪切变形的组合梁滑移和挠度变形理论计算公式.两集中力作用点距跨中各为700mm，钢材弹性模量Es为210GPa，面板和下箱室充填C40现浇混凝土，弹性模量取Ec为32.5GPa.

表1　组合梁截面属性

考虑滑移和剪切变形作用下，试件PSCB2-1，PSCB2-2在负弯矩区的跨中荷载-挠度曲线的实测值和文中计算值对比，如图5所示.由图5可知：理论公式计算值与实测值曲线在弹性阶段相吻合，剪切和滑移双重作用下的挠度变形随着荷载的增加而变得明显，与不考虑剪切滑移效应得到的挠度值相比，差值偏大，尤其是在组合梁弹塑性变形发展阶段.

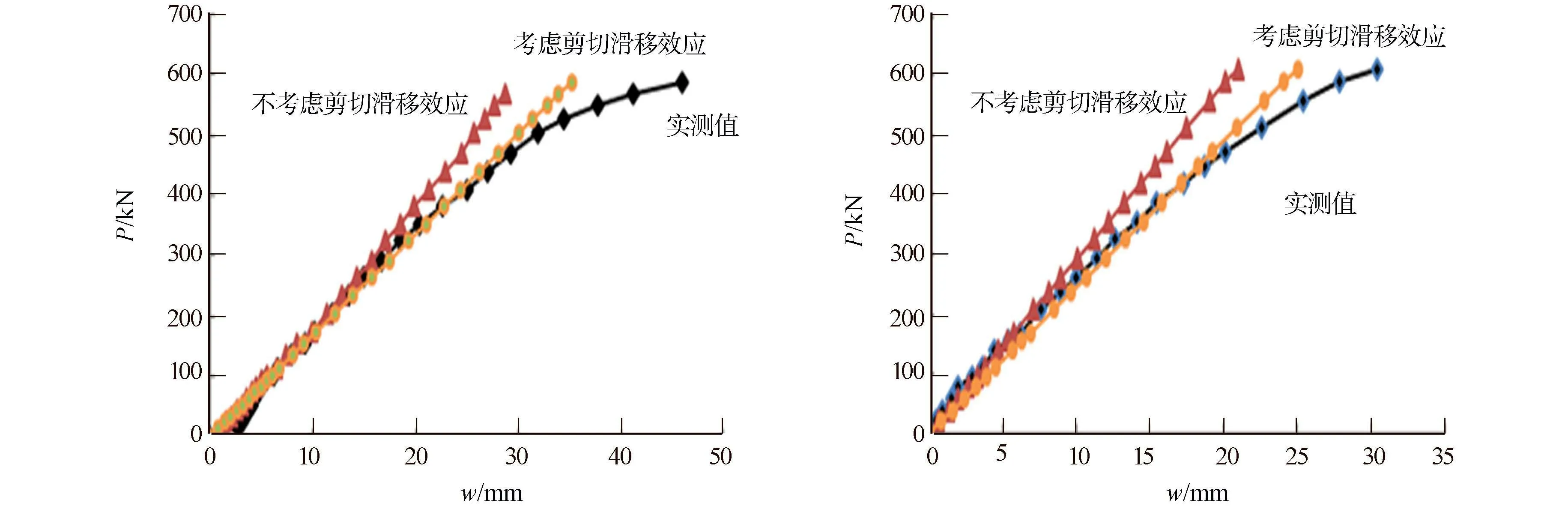
(a) PSCB2-1　　　　　　　　　　　　　　　　(b) PSCB2-2图5　试件的荷载-跨中挠度曲线对比Fig.5　Load-mid-span deflection curves

为了验证组合梁负弯矩区考虑滑移和剪切变形作用下理论公式的正确性，在不同加载状况下，分别验证试件PSCB2-1与PSCB2-2的交界面相对滑移值沿全跨长的变分法理论计算值与试验值差别，结果如图6所示.

由图6可知：滑移曲线基本以跨中对称分布，理论公式计算值与实测值曲线在弹性变形阶段(约为极限荷载的70%)拟合性较高，趋势较为一致.滑移极值点出现在加载点处，沿梁跨到支座处呈下降趋势.由于活动支座在加载过程中发生微小变位，PSCB2-1北梁一侧未出现拐点使得交界面摩阻力减小，计算值与实测值有一定的偏差，但是南端一侧曲线拟合性较好，并不影响计算值曲线的线性分布趋势.总之，PSCB2-1，PSCB2-2具有很好的线性分布计算值，适用性较高.

4结论

1) 结合部分充填式钢箱-混凝土组合梁弯曲滑移变形及剪切变形机理，建立了组合梁变分计算模型.以两广义位移理论和能量变分原理为基础，假定基于微段内力平衡方程得到混凝土板和钢箱换算截面的滑移应变，将各自弯曲应变叠加得到总应变，列出混凝土板、顶板、中隔板、底板、腹板的弯曲应变能及腹板和换算截面钢板的剪切应变能；然后，分别代入组合梁计算模型，通过能量变分最小势能为0的基本原理，并通过分部积分得到能量微分方程及其控制边界条件，得到滑移微分方程和一阶曲率微分方程.最后，对一阶曲率微分方程积分两次，并联立连续性条件和边界控制条件得到组合梁纯弯段和剪弯段挠度方程.此外，增加了剪切变形对附加挠度的修正项，梁的附加弯矩Mf(x)与滑移应变μ′(x)有关，且与E3I3成正比.因而，从理论计算层次上得出组合梁滑移和剪切变形会显著增大组合梁挠度的结论.

2) 通过不同抗剪连接度的试件论证了计算理论值的正确性.在弹性加载阶段(约为极限荷载的70%)，跨中挠度计算值曲线与全梁跨交界面滑移计算值曲线与实测值比较精度值较高.验证了计算模型的适用性，完善了部分充填式钢箱-混凝土组合梁受力变形机理.

参考文献：

[1]莫时旭，周晓冰.部分充填钢箱-混凝土组合梁受力性能有限元分析[J].华侨大学学报(自然科学版)，2015，36(4):455-456.

[2]莫时旭，钟新谷.钢箱-混凝土组合梁抗剪性能试验研究[J].桥梁建设，2007(6):13-16.

[3]李兴科，莫时旭，郑艳，等.部分充填钢箱-混凝土组合梁变形计算[J]. 广西大学学报(自然科学版)， 2015， 40(2):303-305.

[4]樊健生，聂建国.负弯矩作用下考虑滑移效应的组合梁承载力分析[J].工程力学，2005，22(3):177-182.

[5]SCHNABL S，SAJE M，TURK G.Analytical solution of two-layer beam taking into account interlayer slip and shear deformation[J].Journal of Structural Engineering，2007，133(6):886-894.

[6]PAOLO F.Analytical solution of two-layer beam taking into account nonlinear interlayer slip[J].Journal of Engineering Mechanics，2009，135(10):1129-1146.

[7]周勇超，李亮亮，李子青.钢-混凝土组合梁界面滑移效应变分法求解[J].长安大学学报(自然科学版)，2013，33(1):40-43.

[8]贺桂超，周凌宇.考虑剪切和界面滑移的钢-混凝土组合箱梁变分解法[J].中南大学学报(自然科学版)，2012，43(11):34-37.

[9]XU Rongqiao，WANG Guannan.Variational principle of partial-interaction composite beams using Timoshenko′s beam theory[J].International Journal of Mechanical Sciences，2012(60):72-83.

[10]刘哲圆.剪切变形对波纹钢腹板组合箱梁挠度影响研究[D].西安：长安大学，2010:31-39.

(责任编辑： 陈志贤英文审校： 方德平)

Energy Variational Method to Analyze Concrete-Partial-Filled Steel Box Composite Beam Considering Shear Deformation and Slip Effect

MO Shixu1，2， XU Haining1

(1. Guangxi Key Laboratory of Rock-Soil Mechanic and Engineering， Guilin 541004，China;2. College of Civil Engineering and Architecture， Guilin University of Technology， Guilin 541004，China)

Abstract：In order to study the influence of slip and shear deformation to the deformation of concrete-partial-filled steel box composite beams， the differential equations and boundary conditions are established. Based on the generalized displacement theory and energy variational principle of Timoshenk beam， the model and the assumption of the composite beam variational calculation are presented. The combined elastic analytical solutions of the differential equations， deflection and additional moment of the negative moment region of the simple supported composite box girder with double deformation modes are derived by the minimum potential energy principle. Compared with the measured values and theoretical formulas of two composite beams with different shear connection degrees， it′s shown that the deflection and slip calculated by the variational method in the elastic stage agree with the measured values， which proves the validity of the theoretical formula.

Keywords：concrete-partial-filled steel box composite beam； negative moment region； energy variational method； slip deformation； shear deformation

中图分类号：TU 398.9

文献标志码：A

基金项目：国家自然科学基金资助项目(51168011， 51108109)； 广西岩土力学与工程重点实验室科研基金资助项目(11-CX-05)

通信作者：莫时旭(1964-)，男，教授，博士，主要从事钢-混凝土组合结构的研究.E-mail:moshixuwh@yahoo.com.cn.

收稿日期：2015-10-24

doi:10.11830/ISSN.1000-5013.2016.02.0234

文章编号：1000-5013(2016)02-0234-07