探究特殊与一般思想在高考中的应用

■甘肃省张掖市实验中学　王新宏



探究特殊与一般思想在高考中的应用

■甘肃省张掖市实验中学王新宏

*本文为甘肃省教育科学“十二五”规划2013年度课题《新课改理念下高三数学复习高效策略研究》（课题批准号GS【2013】GHB0771）的成果.

综观近几年的全国卷Ⅰ、全国卷Ⅱ、北京卷、浙江卷、湖北卷、福建卷等的最后一道（或几道）选择题或最后一道填空题，不难发现，这些把关题体现特殊与一般数学思想，这些试题集中考查了考生独立思考、自主探究的能力，很好地区分了考生的数学素养与思维品质，以及今后学习数学的潜质，既充分体现了考生的知识技能和思维方法，也给灵活多变的思维，收放自如的想象留下了更大的发挥空间.所以无论是教者还是学者，都应重视这些问题中蕴含的解题思想，在日常的教与学中注意训练、培养相应的能力.

数学思想方法的考查是对考生的数学知识更高层次上的考查，特殊与一般思想是课标课程高考课程的七大数学思想之一，考查时必然以数学知识为载体，来反映考生的数学思想方法的掌握程度.具体来说，高考数学中对它的考查方式主要有：通过寻求特殊值、特殊点、特殊数列、特殊的位置关系等来研究解决不确定问题、运动变化问题、抽象问题等.

辩证法告诉我们：矛盾的特殊性寓于一般性之中.相对于一般情形而言，特殊的事物往往显得简单、直观、具体、形象，并被人们所熟知.解题时若能注意到问题的特殊性，进而分析考虑有无可能把待解决问题转化为特殊问题或极端情形，不仅是可行的，而且会事半功倍.

一、特殊化思想PK一般化思想

在一些高考的把关小题上，既能用一般化的数学思想方法解决，又能用特殊化的数学思想方法解决，但一般性解决时，要么思维上难，要么运算上繁，考生较难找到解决问题的切入点，浪费了宝贵的时间，效率低下，反之若用特殊化数学思想解题，则有效地降低了思维的难度和运算量，效率又高，下面请读者自己辨别、思考、领悟.

1.在函数问题中PK

在求参数范围、函数图像等函数问题中，命题者精心策划，刻意安排考查特殊与一般的数学思想，看你能否想到通过构造特殊函数、寻找特殊点、特殊值来解决这类问题.

例1（2015年全国Ⅰ卷理科第12题）设函数f（x）= ex（2x-1）-ax+a，其中a＜1，若存在唯一的整数x0，使得f（x0）＜0，则a的取值范围是（）.

解析1（一般化思想）：设g（x）=ex（2x-1），h（x）=ax-a.由题意知，存在唯一的整数x0，使得g（x0）在直线y=ax-a的下方.因为g′（x）=ex（2x+1），所以当时，g′（x）＜0；当时，g′（x）＞0，所以当时，［g（x）］min=作出g（x）与h（x）的大致图像如图1所示，故即a＜1，故选D.

图1

点评：考生能由f（x0）＜0能恰当构造函数的有多少？能画出函数草图的又有多少？

解析2（特殊点）：仔细观察可发现f（0）=a-1＜0，所以由题意知，x0=0，则得，结合已知得≤a＜1.故选D.

点评：只要分析出x0=0，问题也就随之破解；数学不是缺少美，而是缺少发现美的智慧.

解析3（特殊值）：根据选项，可以采取特殊值代入验证，从而甄别出正确答案.当a=0时，f（x）=ex（2x-1），f′（x） =ex（2x+1），则f（x）在）递减，在递增，又f（0）=-1＜0，f（-1）=-3e-1＜0，不符合题意，故a=0不成立，排除答案A，B；当时，因为为增函数，且所以存在t∈（-1，0），使得f′（t）=0，则f（x）在（-∞，t）递减，在（t，+∞）递增，又故存在唯一的整数0，使得f（0）＜0，即满足题意，排除答案C，选D.

点评：特例排除法是解决一般化思想做不出来或不好做而常用的行之有效的一种解题方法，但相当一部分学生缺乏利用它来解题的意识，不是他做不到，主要是他想不到.

例2（2015年全国卷Ⅱ理科第10题）如图2，长方形ABCD的边AB= 2，BC=1，O是AB的中点，点P沿着边BC，CD与DA运动，记∠BOP=x.将动P 到A、B两点距离之和表示为x的函数f（x），则y=f（x）的图像大致为（）.

解析1（一般化思想）：由已知得，当点P在BC边上运动时，即时当点P在 CD边上运动时，即时，PA+PB=当时，PA+PB=当点P在AD边上运动时，即时，PA+从点P的运动过程可以看出，轨迹关于直线对称，且，且由解析式可知，轨迹为非线性.故选B.

点评：烦琐，小题大做，浪费了宝贵的时间.

点评：小题要巧做，赢得时间就是你赢得高分的保证.

2.在三角函数问题中PK

一些四边形中的三角函数问题或是涉及到三角函数的图像问题，难以找到解决问题的切入口，可通过构造满足题意的特殊三角形，让问题的实质原型暴露出来，或是绘出满足题意的一个特殊的三角函数图像，借助图像的直观性，快速准确地解决此类问题.

例3（2015年全国卷Ⅰ理科第16题）在平面四边形ABCD中，∠A=∠B=∠C=75°，BC=2，则AB的取值范围是_________.

解析1（一般化思想）：如图3所示，连接AC，设∠BAC=α，则∠ACB=105°-α.在△ABC中，

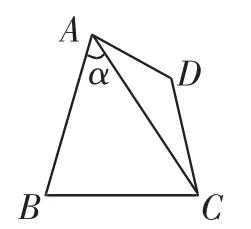
图3

点评：填空题末题，切入难，运算繁，区分度强.

解析2（特殊图形）：如图4所示，延长BA，CD交于E，平移AD，当A与D重合与E点时，AB最长，在△BCE中，∠B=∠C=75°，∠E=30°，BC=2，由正弦定理可得，即，解得；平移AD，当D与C重合时，AB最短，此时与AB交于F，在△BCF中，∠B=∠BFC=75°，∠FCB=30°，由正弦定理知，即，解得.所以AB的取值范围是

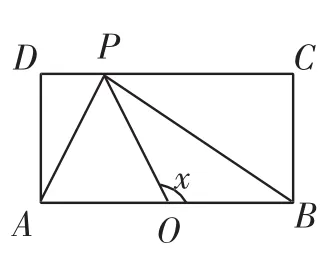
图2

图4

点评：不怕你做不到，就怕你想不到；善于通过联想，把所求知识与自己所掌握知识恰当融合，是一种数学能力的体现.

例4（2014年北京卷理科第14题）设函数f（x）=sin（ωx+φ），A＞0，ω＞0，若f（x）在区间上具有单调性，且，则f（x）的最小正周期为________.

解析2（特殊图形）：画出满足题意的一个草图如图5所示，设f（x）的最小正周期为T，则，即T≥，所以，即T=π.

图5

点评：此题大部分学生缺乏找“特殊图形”的意识，所以很难优质高效地解决此题；通过长时间的教育教学，我们发现数学成绩优异的学生与普通学生相比，差别主要有两点，第一，会不会合理地将问题等价转化为熟悉的问题来解决；第二，会不会运用数形结合的思想方法解题.

3.在数列问题中PK

一些高考数列问题，表面看起来比较抽象、复杂，很难下手，如果使问题退化到最为简单的“原始”特殊数列就可化抽象为具体，变复杂为简单，问题也就迎刃而解了，总之，以退为进，退到一个能够下手处理的位置，从而达到解决一般问题的目的，可谓“退一步海阔天空”.

例5（2015年湖北卷理科第5题）设a1，a2，a3，…，an∈R，n≥3.若p：a1，a2，a3，…，an成等比数列；q：，则（）.

A.p是q的充分条件，但不是q的必要条件

B.p是q的必要条件，但不是q的充分条件

C.p是q的充分必要条件

D.p既不是q的充分条件，也不是q的必要条件

解析1（一般化思想）：对命题p：a1，a2，…，an成等比数列，则公比a且an≠0.

对命题q，①当an=0时成立；

②当an≠0时，根据柯西不等式，等式成立，则所以成等比数列.

所以p是q的充分条件，但不是q的必要条件.

点评：考生能联想到柯西不等式的有多少？能想到柯西不等式取“=”的条件的又有多少？

解析2（特殊数列）：取大家最熟悉的等比数列an=2n，代入q命题（不妨让n=3）满足，再取an=3n代入q命题（不妨让n=3）也满足，反之取a1=a2=a3=…=an=0，满足q命题，但不满足p命题，故是的充分条件，但不是的必要条件.

点评：这类题，一般的方法很难解决，但特殊数列法思路简单，运算直接明了，简单就是数学的一种美.能得分的方法都是好方法，取特例时，越简单越熟悉越好.

4.在立体几何问题中PK

立体几何中有关运动变化的点（或图形）的问题，常考虑极限位置，特殊化处理，往往收到意想不到的效果，真叫人拍案叫绝，连声叫好.

例6（2015年浙江卷理科第8题）如图6，已知△ABC，D是AB的中点，沿直线CD将△ACD折成△A′CD，所成二面角A′-CD-B的平面角为α，则（）.

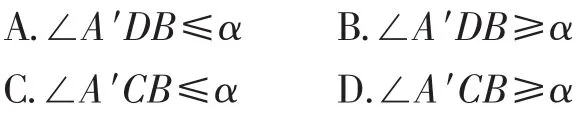
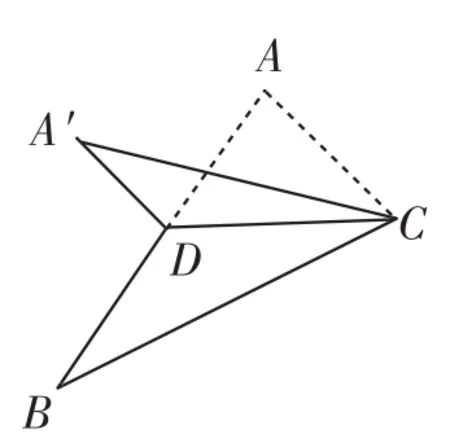
图6

图7

解析1（一般化思想）：如图7所示，设∠ADC=θ，AB=2，则有题意知，AD=BD=A′D=1.在空间图形中，连接A′B，设A′B=t，在△A′DB中，过A′作A′N⊥DC，过B作BM⊥DC，垂足分别为N、M，过N作NP∥=MB，使四边形BPNM为矩形，则NP⊥DC，连接A′P，BP，则∠A′NP就是二面角A′－CD－B的平面角.所以∠A′NP=α，在Rt△A′ND中，DN=A′Dcos∠A′DC=cosθ，A′N=A′Dsin∠A′DC=sinθ.同理，BM=PN=sinθ，DM=cosθ，故BP=MN=2cosθ，显然BP⊥平面A′NP，故BP⊥A′P.

在Rt△A′BP中，A′P2=A′B2－BP2=t2－（2cosθ）2=t2－4cosθ2，

点评：太烦琐了，这绝不是命题者的初衷，更不是数学的追求，根本无法体现数学的美与精神.

解析2（极限位置）：若CA≠CB，则当α=π时，∠A′CB＜π，排除D；当α=0时，∠A′CB＞0，∠A′DB＞0，可排除A、C，故选B.

点评：大浪淘沙始见金，想得越深刻，思考得越开放，方法就越简单，越能体现数学的美与精神.

5.在圆或圆锥曲线问题中PK

一些有关圆与直线或圆锥曲线与直线的问题中，总让人有蒙着一层神秘的面纱，或是雾里看花的感觉，题目中点多，未知的量较多，运动的点也较多，如何透过层层迷雾，摘掉它的神秘面纱，这就需要用特殊化思想找到特殊的点（或线、曲线），从而迅速破解问题.

例7（2014年湖北卷文科第17题）已知圆O：x2+y2=1和点，若定点B（b，0）（b≠－2）和常数λ满足：对圆O上任意一点，都有|MB|=λ|MA|，则：

（Ⅰ）b=_________；（Ⅱ）λ=_________.

解析1（一般化思想）：设M（x，y），则x2+y2=1，y2=1－x2，因为λ为常数，所以，解得或b=－2（舍），所以，解得或（舍）.故

解析2（三角换元）：在圆O上任意取一点M（cosθ，sinθ），则由|MB|=λ|MA|可得整理得1+b2－5λ2－（2b+4λ2）cosθ=0，即解得

解析3（特殊点）：既然对圆O上任意一点，都有|MB|= λ|MA|，使得λ与b为常数，那么我们何不把点取为特殊点呢？取M（1，0）与M（0，1）代入|MB|=λ|MA|得：解得

点评：大部分考生想不到特例法，主要原因是他们对特殊与一般的数学思想理解得不够深刻，不够到位，再加上平时训练的又较少甚至没有，故想不到简便的解题策略.

6.在抽象函数问题中PK

在抽象函数中，只有根据具体情况巧妙赋值，方可化“腐朽”为“神奇”.

例8（2015年福建卷理科第10题）若定义在R上的函数f（x）满足f（0）=-1，其导函数f′（x）满足f′（x）＞k＞1，则下列结论中一定错误的是（）.

解析1（一般化思想）：由已知条件，构造函数g（x）= f（x）－kx，则g′（x）=f′（x）－k＞0，故函数g（x）=f（x）－kx在R上单调递增，且，故所以故结论中一定错误的是C；选项D不确定；构造函数h（x）=f（x）－x，则h′（x）=f′（x）－1＞0，所以函数h（x）=f（x）－x在R上单调递增，且故所以选项A，B无法判断，故选C.

解析2（特殊函数）：令f（x）=2.1x－1，且k=2，则，所以A正确；令f（x）=6x－1，且k=2，则1，所以B正确，f（1）=5＞2，所以D正确；C错误.

二、有直接法可用吗

在用坐标法求解的向量问题，大多数抽象函数问题，不确定函数问题，某些数列性质的探究问题，不是不想用一般化思想方法解题，而是有一般化思想方法可用吗？

A.13B.15C.19D.21

解析：建立如图8所示的平面直角坐标系，画满足题意的一个草图，所以所以（当且仅当，即时取等号），所以的最大值为13，故选A.

图8

点评：坐标化是处理平面向量问题最简单，最有效的方法.

三、特例探路，结合演绎推理得出一般结论

由特殊探路，让合情推理与演绎推理协同作战来解决一般性问题，解题的过程就会层次分明，显得非常优美，提高了数学思维的流畅性，这也是数学中特殊与一般思想的重要体现.

例10（2014年新课标全国卷Ⅱ理科第16题）设点M（x0，1），若在圆O：x2+y2=1上存在点N，使得∠OMN=45°，则x0的取值范围是________.

图9

解析：如图9，点M（x0，1）在直线y=1上，且y=1与圆O：x2+y2=1相切于点M（0，1），此时圆O：x2+y2=1上存在点N（1，0）或N（-1，0），使得∠OMN= 45°；当点M为（-1，1）或（1，1）时，作圆O的切线，得切点为N（1，0）或N（-1，0），使得∠OMN=45°，满足题意；故当M（x0，1）中的-1＜x0＜1时，过点M（x0，1）作圆O的切线，切点为点N′，则∠OMN′＞45°，所以在圆O上存在点N，使得∠OMN= 45°；若x0＜-1或x0＞1时，过点M（x0，1）作圆O的切线，切点为点N′，则∠OMN′＜45°，所以在圆O上不存在点N，使得∠OMN=45°.

综上：-1≤x0≤1.

点评：本题数形结合将一般问题特殊化，将不熟悉的问题等价转化为熟悉的问题，合理分析，推敲得出答案，设计质朴，但思维发散，不容易找到切入点与临界点，很好的测试了考生的数学素养与学习潜能.

四、巩固练习

高考中像这样运用特殊化思想解决一般性问题的机遇多吗？要知道高考命题者出于试卷的“信度”和“效度”的需求，不会用十分古怪的问题来刁难考生，所以这样的机遇还是不少的，关键是你能否敏锐地发现它，捕捉它，然后利用特殊化思想解决它.

2.（2015年全国Ⅱ卷文科第12题）设函数f（x）=ln（1+，则使得成立的的取值范围是（）.

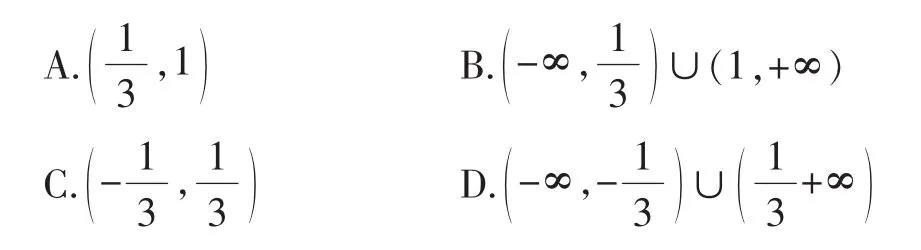
3.（2015年浙江卷文科第6题）有三个房间需要粉刷，粉刷方案要求：每个房间只用一种颜色，且三个房间颜色各不相同.已知三个房间的粉刷面积（单位：m2）分别为x，y，z，且x＜y＜z，三种颜色涂料的粉刷费用（单位：元/m2）分别为a，b，c，且a＜b＜c.在不同的方案中，最低的总费用（单位：元）是（）.

A.ax+by+czB.az+by+cx

C.ay+bz+cxD.ay+bx+cz

4.（2015年湖北理科第8题）将离心率为e1的双曲线C1的实半轴长a和虚半轴长b（a≠b）同时增加m（m＞0）个单位长度，得到离心率为e2的双曲线C2，则（）.

A.对任意的a，b，e1＞e2

B.当a＞b时，e1＞e2；当a＜b时，e1＜e2

C.对任意的a，b，e1＜e2

D.当a＞b时，e1＜e2；当a＜b时，e1＞e2

答案：1.C2.A3.B4.D

参考文献：

1.童其林.特殊与一般思想在解题中的运用［J］.中国数学教育，2013（3）.

2.朱日华．特殊与一般思想在解填空题中的应用［J］.中学数学月刊，2012（10）.

3.倪富春．特例法在解选择题中的妙用［J］.中学数学（上），2014（3）.