小议试题讲评多解性的重要性

■江苏省如皋市搬经中学　何竹峰



小议试题讲评多解性的重要性

■江苏省如皋市搬经中学何竹峰

众所周知，数学解题教学立足于学生对于数学知识在具体问题中的使用熟练度，这与解题训练密不可分．对于解题效果最直接的体现，是试卷中学生对于解决的问题所产生的一些误区，这些错误往往千奇百怪、思维发散，因此笔者以为对于试卷中重要的数学问题要给出多样性的回应，这正如解题教学泰斗罗增儒先生所说：解题教学要有效需要两个方面，其一是给出较好的方法，引导学生解决问题中用较好的方式处理，但这还只是第一层境界；学生解题的方式比较多、思维比较开阔，恰是这种开阔性才能激发学生的创新精神，将不同的问题解决思路多种展示，是第二重境界．

从试题讲评的多解性来看，笔者以为至少有下列两个优点：

（1）思维发散性：思维培养是数学教学最重要的作用，试题讲评多解性的渗透恰恰是培养学生思维的发散性，如代数问题既能给出一般性的代数解法，又能给出巧妙的几何方式，自然对于学生思维启发有着较大的作用.

（2）熟练整合度：多解性的使用，自然会使用到各种不同的知识，讲评中多次使用不同知识既提高了知识的熟练度，也提高了知识的整合度．

下文笔者以两大几何问题为例，小议在几何问题讲评中多解性的分析．

一、立体几何中的多解性渗透

案例1如图1，在四棱锥PABCD中，PA⊥平面ABCD，底面ABCD是平行四边形，∠BAD= 120°，PA=AD=1，AB=2．M、N分别是PD、CD的中点，求二面角AMN-C的余弦值．

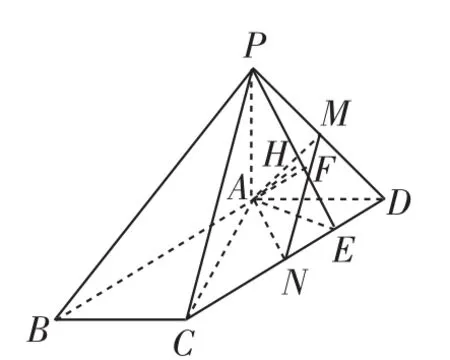
图1

分析：二面角问题始终是我们学生的一大弱点，所以此题大部分学生都没能用传统方法找出二面角的平面角，而用空间直角坐标系的也有很多的问题：有建错系的，有写错点坐标的，有计算错误的，还有最后不会判断锐角钝角的.最后在和同学们的共同探讨中，主要形成了以下三种方法：

方法一：如图1所示，在等边△AND中取DN中点E，连AE，PE，在直角△PAE中作AH⊥PE于点H，则AE⊥CD，PA⊥CD，所以CD⊥平面PAE.于是CD⊥AH，又AH⊥PE，所以AH⊥平面CMN.在△AMN中，过A点作AF⊥MN于点F.因为AH⊥平面CMN，所以AH⊥MN.故MN⊥平面AFH，于是有FH⊥MN，结合AH⊥MN，所以∠AFH为二面角A-MN-C的平面角.

方法二：直接找二面角有点困难，所以可以转化为先求二面角A-MN-D，易知AN=MN=ND=1，AM=MD=，所以△AMN和△DMN全等，则只要作DO⊥MN，交MN于O，连接AO，则AO⊥MN，则∠AOD即为所求二面角的平面角.易求得，则二面角A-MN-C平面角的余弦值为

方法三：以A为坐标原点，AC、AD、AP所在直线为坐标轴，建立如图2所示的空间直角坐标系，则设n=（x1，y1，z1）是平面AMN的法向量，可得

图2

说明：空间几何问题笔者以为要教会学生“两条腿”走路，其一是传统法，即如何求解二面角，这里往往涉及到定义法等，这些方法的使用较好地厘清了学生的立体几何公理化体系，尤其对于立体几何小题中的稍难问题更有独到的作用；其二是空间向量法的使用，吴文俊大师提出了数学问题“代数化”的方式，这种机械化的方式被认为是解决空间几何最为一般化的方式.教学中对两种不同方法的引导，有助于学生在问题解决中合理地使用方法.

二、解析几何中的多解性简化

案例2已知正六边形ABCDEF的边长是2，一条抛物线恰好经过该六边形的四个顶点，则抛物线的焦点到准线的距离是____________.

分析：首先本题部分学生不会做的原因是觉得这个六边形怎么放置有疑问，从而觉得此题因存在不确定因素而难以下手.而灵活的同学则发现不管正六边形怎么放置，只要是抛物线过四个顶点，则抛物线的形状是不变的，那么p的值也是不变的，因此在优秀学生中主要有以下解法：

方法一：学生发现本质是待定系数法求二次函数的解析式，属初中内容，所以设二次函数y=ax2+b，如图3，建立直角坐标系代入易求得a=，所以

图3

方法二：如图4，设x2=2py，设A（1，h），，则计算得

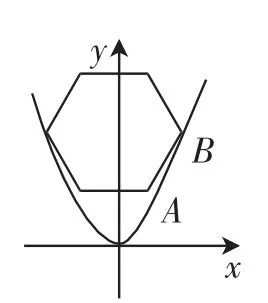
图4

通过本题的讲评，笔者还让同学们尝试编了同类型试题如下：

（1）已知正六边形ABCDEF的边长是2，一个椭圆恰好经过该六边形的四个顶点，并且另外两个顶点为该椭圆的焦点，则椭圆的离心率为_______________.

（2）已知正六边形ABCDEF的边长是2，某双曲线恰好经过该六边形的四个顶点，并且另外两个顶点为该双曲线的焦点，则双曲线的离心率为_______________.

（Ⅰ）设椭圆C1的左焦点为F1，右焦点为F2，直线l1过点F1且垂直于椭圆的长轴，动直线l2垂直于l1，垂足为点P，线段PF2的垂直平分线交l2于点M，求点M的轨迹C2的方程；

（Ⅱ）若AC，BD是经过椭圆C1右焦点F2的两条互相垂直的弦，求四边形ABCD面积的最小值.

分析：（Ⅰ）考查求轨迹方程的问题.求轨迹方程的方法有很多：直接法、转移代入法（相关点法）、参数法、定义法等.在讲评过程中发现很多学生是采用参数法求得的，但是运算上正确率较低.

方法一：设直线l2：y=y0，则线段PF0的垂直平分线为，与y=y0的交点M设为（x，y），得消参即可得到y2=4x，即为所求点的轨迹方程.

方法二（定义法）：发现符合定义的同学较少，说明对此类问题学生在综合分析能力及化归转化思想的应用上有所欠缺.解法如下：由题意得|MP|=|MF2|，故动点M到定直线l1：x=-1的距离等于它到定点F2（1，0）的距离，所以动点M的轨迹C2是以l1为准线，F2为焦点的抛物线.因此所求点M的轨迹方程C2为y2=4x，抓住问题的本质后，解题过程简洁明了.

（Ⅱ）在讲评过程中，学生反映出的问题主要有两个：计算问题和求函数最值方法问题.通过和同学们的一起探讨，最后笔者主要用了三种方法求最值：易知，当直线AC的斜率不存在或斜率为零时，四边形ABCD的面积S=4，其他情况四边形ABCD的面积为

方法一：基本不等式求最值，由于（2k2+3）（2+3k2）≤，所以，当2k2+3=2+ 3k2，即k=±1时取等号.

方法三（换元法）：本题到最后学生对求最值感到困难的一大原因是因为式子复杂、次数又高而产生惧怕心里，从而失去了正常的分析能力，所以笔者对这样的问题在教学时一直是以复杂问题简单化，如何先转化为我们熟悉的问题为重点教学的，所以本题笔者又通过设t= 1+k2，

所以当t=1+k2=2，即k=±1时，S有最小值

说明：解析几何问题的处理主要集中在两个方面的引导：其一是题中条件转换是否合理？如：我们知道以AB为直径的圆经过F点之类的条件，最合理、最简洁、最高效的方式是利用向量条件而多数学生却在求解圆方程，利用距离求解，令人费解；其二是如案例3中所述，解析几何中的最值如何求解？即函数模型的处理.笔者以为，这是多解性方法可以优化的地方，优化合理的函数模型更有利于学生感悟函数最值求解的重要性，也对解析几何问题不再恐惧.

总之，试题讲评多解性对于学生思路的开拓性、知识的整合性以及错误的纠正性上都有较为有效的作用，笔者建议在合理的、重要的试题中引入讲评的多解性，有助于解题教学展开得更为高效、有效.

参考文献：

1.姚连省.让学生自己写试卷分析［J］.考试周刊，2010（12）.

2.姜兴荣.探求解题思路的几种有效策略［J］.中小学数学，2013（7-8）.

3.朱永祥.再谈数学思想方法的挖掘和应用［J］.中学数学（上），2008（2）.