也谈“RMI原理”与仿射变换下有关圆与椭圆的若干问题*

■重庆育才中学　王历权■重庆育才中学　党忠良■重庆育才中学　郭晓俊



也谈“RMI原理”与仿射变换下有关圆与椭圆的若干问题*

■重庆育才中学王历权
■重庆育才中学党忠良
■重庆育才中学郭晓俊

文［1］中，俞建英、蒋亮两位老师给出了“RMI原理”的工作机制，如图1，证明了映射的若干性质，还给出了映射φ的若干应用实例.本人深受启发，结合日常教学中的一些思考，再谈谈“RMI原理”下有关圆与椭圆的若干问题，请同行斧正.

*本文系重庆市教育科学“十二五”规划课题（课题批准号：2014-00-021）《基于促进学生理解数学本质的中学数学核心概念及思想方法的教学实践与评价研究》的部分研究成果.

图1

一、仿射变换与“RMI原理”

解析几何中的仿射变换即是RMI原理的具体应用.事实上，文［1］中的映射是最简易的仿射变换，这里先给出一般情形下的二维仿射变换，其相关性质详见文献［1］.

图像的压缩、平移、旋转都是常见的仿射变换，比如，反比例函数的图像是双曲线，在直角坐标系中，函数的图像上任取一点P（x，y），设x轴正向逆时针旋转至与OP重合时所转过的最小正角为θ，令现将OP顺时针旋转得到P′（x′，y′），则有因此得到

又xy=1，所以有x2′-y2′=2，其图像等轴双曲线，由于旋转不改变曲线形状，故函数的图像是双曲线.

图形经过任何仿射变换后都不变的性质（量）称为图形的仿射性质（仿射不变量）.

性质1两个三角形面积之比是仿射不变量.

证明：在笛卡尔坐标系下，不共线三点P1（x1，y1），P2（x2，y2），P3（x3，y3）经过仿射变换后，对应点为P1′（x1′，y1′），P2′（x2′，y2′），P3′（x3′，y3′），于是因此（定值）.

性质2两个封闭图形面积之比是仿射不变量，且其面积的比例仍为|a11a22-a21a12|.证明此处略.

二、从仿射变换看圆与椭圆的互相变换

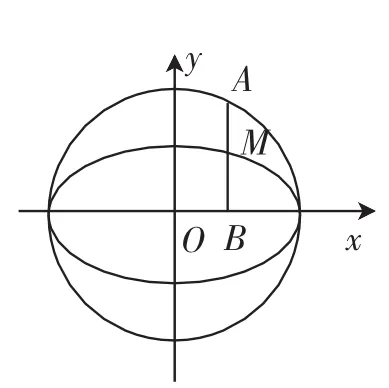
图2

问题1中学教材上有一道经典例题，如图2，已知点A是圆x2+y2= 4上一动点，AB⊥x轴，垂足为B，求线段AB中点M的轨迹方程.

问题2学生学习完圆锥曲线一章后都知道平面斜着切割圆柱得到截面痕迹为椭圆，针对这个问题，无论教材还是各类教辅都直接告知结论，思维严谨的学生马上就会想到这个结论是观察得到的还是理论证明的？如果说是直观感受得到的结果，那么他们会说直观上得到的认识是感性认识，而感性认识未必可靠；如果说是理论上推导出来的，那么他们会问这个问题该如何推导？本文采用仿射变换的方法证明这个结论.

如图3，设圆柱底面β半径为r，一平面α与圆柱相交，与圆柱中轴线交于点O，与圆柱底面交于点A，设α与β所形成的二面角的平面角大小为建立如图3所示直角坐标系x1-O1-y1，使得y1轴与平面α垂直，在平面α中以点O为坐标原点，AO所在直线为x轴建立直角坐标系x-O-y，则y轴与y1轴平行.

图3

在截面痕迹上任取点P（x，y），过P作圆柱的母线，与底面圆交于点P1（x1，y1），则有x21+y21=r2，如图可知，因此在仿射变换φ的作用下，圆的方程变为x2cos2θ+y2=r2，即其中显然有这是一个椭圆的标准方程，并且还得到一个美妙的结论：

三、仿射变换下圆与椭圆的面积

由性质2和圆、椭圆的封闭型可知，圆与椭圆的面积间存在着某种强烈的关联，我们也可以用积分等办法求出椭圆的面积，这里谈谈仿射不变量性质在证明相关椭圆面积时的简单应用.

问题3求椭圆的面积.

问题4如图4，从椭圆外一点P引椭圆两条切线PA，PB，O为坐标原点，设OP交椭圆于点C，求证：S△AOC= S△BOC，S△AOP=S△BOP.

图4

图5

证明：如图5，S△A′O′C′=S△B′O′C′，S△A′O′P′=S△B′O′P″是显然的，因此由性质1知，原命题成立.

事实上，由此还可以得到上述三角形的另一个性质：

性质3图4椭圆中，PO平分弦AB.

有了性质3，事实上就又产生了一种证明问题4的方法.

四、仿射变换下圆与椭圆的阿基米德三角形

如图6，过圆锥曲线的弦两端的切线与弦所围成的三角形称为阿基米德三角形，类似可以定义圆的阿基米德三角形：过圆的弦（非直径）两端的切线与弦所围成的三角形称为阿基米德三角形.

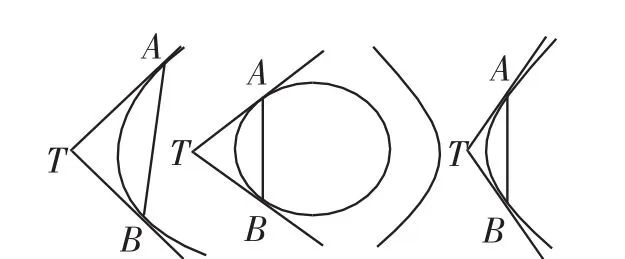
图6

椭圆的阿基米德三角形拥有众多大家所熟知的性质，比如：

特别地，当m=c（-c）时，点P（m，0）即为椭圆的右（左）焦点，直线即为椭圆的右（左）准线.

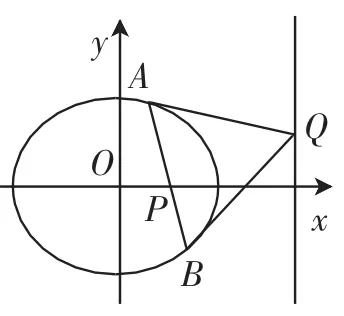
图7

上述两个性质的证明在很多文献中可以看到，本文略.我们知道，椭圆可以经过仿射变换得到对应图形圆：x′2+y′2=a2，因此可以猜想圆的阿基米德三角形也拥有两个与椭圆类似的有趣性质.本文用一般方法和仿射变换的方法证明之.

性质4′：圆C′：x′2+y′2=a2的阿基米德三角形中，弦A′B′绕着圆内定点P′（m′，0）转动时，阿基米德三角形另一个顶点Q′在一条垂直于x轴的直线上运动.

证明（证法1）：设圆的方程是C′：x′2+y′2=a2，弦A′B′的方程为x′=ty′ +m′，联立消去x′，得（t2+1）y′2+2m′ty′+m′2-a2=0.

设A（x1，y1），B（x2，y2），

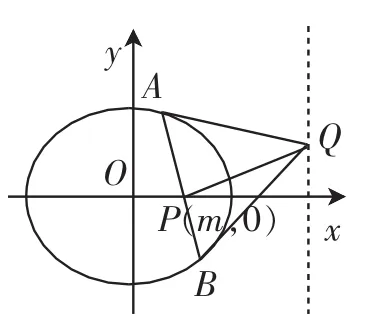
图8

（定值，此处假设点弦A′B′不关于y轴对称）.

证明（证法2）：由文［1］可知，仿射变换φ不改变直线与直线、曲线间的相交、相切、相离等位置关系，因此，A′Q′，B′Q′仍与圆C′相切，且A′Q′∩B′Q′=Q′.显然，在φ：的作用下，有m′=m，直线因此，xQ′=，即点Q′仍在直线上运动，定理4′得证.

性质5′：圆C′：x′2+y′2=a2的阿基米德三角形为A′B′Q′，弦A′B′绕着圆内定点P′（m′，0）转动时，直线A′Q′，P′Q′，B′Q′的斜率成等差数列.

证明（证法2）：由文［1］知，若在仿射变换下直线l对应于直线l′，则有即

因此直线A′Q′，P′Q′，B′Q′的斜率成等差数列.

参考文献：

1.俞建英，蒋亮.“RMI原理”下的椭圆研究［J］.中学数学教学参考（上），2014（12）.

2.林吕根，许子道.解析几何［M］.北京：高等教育出版社，2001.

3.梅向明.高等几何［M］.北京：高等教育出版社，2004.

4.陈光明.把握核心本质，万变不离其宗——菱形视角下圆锥曲线问题的解答［J］.中学数学（上），2015（6）.