基础自然得 能力天然成——对一次联考试卷讲评课的思考

■安徽省灵璧第一中学　郑　良　谢　超



基础自然得能力天然成——对一次联考试卷讲评课的思考

■安徽省灵璧第一中学郑良谢超

一、问题提出

2016年安徽省高考将进入全国卷统考模式.学校为使教师与学生尽快适应新的考试形式，组织高三学生（于2015年11月14、15日）参加安徽省“江淮十校”2016届第二次联考（试卷由一直使用全国卷的地区负责命制，内容包括集合与简易逻辑、函数、导数、三角函数、解三角形、平面向量、复数、数列），还安排学科组进行“试卷讲评”等教研活动.笔者认真观摩并详尽记录，分析领悟受益匪浅，下面针对试卷讲评给出自己的教学思考，不足之处求教于同仁.

二、试题讲评过程呈现

限于篇幅，本文不再以师生对话的形式展示课堂教学，同时对命题组提供的答案以思路方法形式呈现，以便读者能通晓教学全貌.

针对学生按部就班采用“直译法”（先化简复数z，确定复数z后求|z|），教师给出另解后指出：准确理解识记的结论能为解题确定直觉方向，通过对比分析确定解题的切入点、理性思考选取合理的解题思路与方法.本题从“大处着眼”准确地利用复数的运算性质优化了解题的过程.

例2（第9题）已知平面向量a、b（a≠0、b≠0），满足|a|=3，且b与b-a的夹角为30°，则|b|的最大值为（）.

A.2B.4C.6D.8

针对少数学生利用代数法（记|b|=x＞0，θ=〈a，b〉，则0°＜θ＜180°，得，当且仅当θ=60°等号成立，平方后开方易增解x=3cosθ-求解，引导学生从几何角度解决.

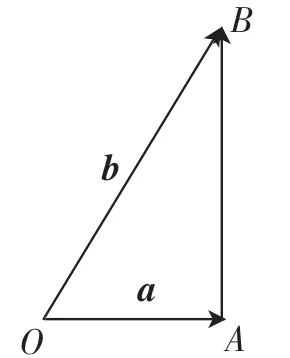
图1

教师引导学生审视条件与结论：已知三角形的一边及对角（确定三角形外接圆的半径），求另一边.从运动的观点看，当OB为三角形外接圆的直径时，|b|取得最大值6.学生自觉构建一个微专题：

链接1（第6题）已知△ABC的三个内角A、B、C所对的边分别是，则△ABC的面积的最大值为（）.

链接2（第18题）已知f（x）=2sinωx（0＜ω＜1）在上的最大值为，当把f（x）的图像上所有点向右平移个单位后，得到的函数g（x）的图像关于直线π对称.

（Ⅰ）求函数g（x）的解析式；

（Ⅱ）在△ABC中，角A、B、C所对的边分别是a、b、c，已知函数g（x）在y轴右侧第一个零点为C，c=4，求△ABC的面积S的最大值.

图2

以第18题为例，通过对三种方法（正弦定理构建目标S的函数、余弦定理建立关于a与b的方程利用不等式放缩得ab的范围、几何背景解释）的比较，使学生透过现象看本质，明晰各种解法的优点与缺点，深切体会审题的重要性.教师强调解题要抓住变与不变的辩证与统一的关系，巧妙实施“以静制动”、“动静结合”等解题策略，并给出各种变式：如条件不变，求△ABC的面积、周长的范围等.

变式（第16题）已知直角△ABC的两直角边AB、 AC的边长分别为方程的两根，且AB＜AC，斜边BC上有异于端点B、C的两点E、F，且EF= 1，设∠EAF=θ，则tanθ的取值范围为___________.

图3

很多学生反映想不出命题组提供的解题思路（以A为坐标原点，分别以AB，AC为x，y轴建立坐标系，利用合理建立坐标系并确立目标函数，不仅对接学生认知，而且使解法更简洁.

例3（第12题）设点P在曲线y=ex上，点Q在曲线y=上，则|PQ|的最小值为（）.

解：在同一坐标下画出函数f（x）=ex与函数的图像，如图4中的曲线C1与C2，其中曲线y=ex在点A（0，1）处的切线方程为l1：y=x+1，可证ex≥x+ 1，当且仅当x=0等号成立；曲线在点B（1，0）处的切线方程为l2：y=x-1，可证，当且仅当x=1等号成立；而直线AB与平行线l1，l2均垂直，故曲线C1与C2的距离为

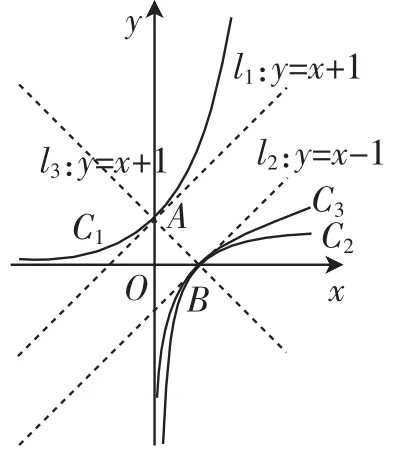
图4

由y=ex联想其反函数y=lnx（其图像为曲线C3），能否用y=lnx作为y=x-1与的“隔离”函数呢？可以证明，对于任意x＞0时，均为，当且仅当x=1时等号成立，故有C1与C2的距离不小于C1与C3的距离，而C1与C3的距离即为|AB|，而A，B分别在曲线C1与C2上，所以

对于教材中的结论（x-1≥lnx）的变式x-1≥lnx≥1-，你见过与它相关的题目吗？你能利用它吗？

综上所述，实数k的取值范围为（－∞，2］.

方法2：上同解法1，故存在x0＞1使得h（x0）=0，即函数g（x）在［1，x0］上单调递减，在（x0，+∞）上单调递增，而g（1）=2－k＜0与x≥1时g（x）≥0恒成立矛盾.

综上所述，实数k的取值范围为（－∞，2］.

方法3：记g（x）=xlnx+x+lnx+1－kx（x≥1），即当x≥1时，g（x）≥0恒成立.

当k≤3时，h（1）=3－k≥0，则g′（x）=h（x）≥0，故函数g（x）在［1，+∞）上单调递增，当x≥1时，g（x）≥0恒成立，只需g（1）=2－k≥0，解得k≤2，所以k≤2；

当k＞3时，h（1）=3－k＜0，函数h（x）在［1，+∞）上单调递增，且h（ek）=e－k+2＞0（当x趋于正无穷大时，h（x）趋于正无穷大），故存在x0∈（1，ek）使得h（x0）=0，即函数g（x）在［1，x0］上单调递减，在（x0，+∞）上单调递增，所以函数g（x）在［1，+∞）上存在唯一的极小值，也是函数g（x）的最小值，因为x≥1，g′（x）＞0，即函数g（x）在［1，+∞）上单调递增，又g（1）≥0，满足题意.

综上所述，实数k的取值范围为（－∞，2］.

含参数的（不）等式的“恒成立”或“存在”问题，常用“分离参数法”或“函数最值法”求解.命题组提供的答案为分离参数法，由，记m（x），问题转化为求函数m（x）的最小值，这要求函数m（x）的最小值易求；若用最值法求解，直接作差构造函数较为困难，而将化分式为整式，有利于求导计算.方法1对参数k分类讨论，对于k＞3通过“设而不求”确定函数g（x）的最小值g（x0），通过结论“lnx≤x－1（当且仅当x=1时等号成立）”估算g（x0）；方法2利用数形结合，从函数g（x）的端点值（必要条件，否定一个命题只需一个反例）进行排除，彰显解法的灵活性；方法3通过必要性解题策略方法，通过特殊值（结论成立的必要条件）来压缩结论的取值空间，只需在相对（于条件）小的范围内确定参数k的取值范围，进而减少或避免对参数的分类讨论，提高了解题效率.

将①的左边、右边分别看成数列{an}，{bn}的前n项和Sn，Tn，只需对任意的k∈N*都有ak≥bk（k从1到n，ak不恒等于bk）即可将ln［n（n+（此为①成立的充分条件）抽象成lnx＞，此命题已在第（Ⅱ）问证实，也可由第12题的结论得到

（Ⅰ）若f（x）在区间（m，m+1）上存在极值，求实数m的取值范围；

先证明当x＞1时，有（lnx+1）（x+1）＞2x⇔xlnx+lnx－x+ 1＞0.记故g（x）在［1，+∞）上单调递增，因此，对任意x＞1，有g（x）＞g（1）=0，故有

若不分离ex与lnx，难以求导确定其极值点（最终目的是确定函数单调性），尝试将ex与lnx分离成g（x）＞h（x）形式，利用其加强命题［g（x）］min≥［h（x）］max（其中g（x）的最小值点与h（x）的最大值点不相同）.通过观察发现，当x=1（起点）时，g（x）=h（x）=2（第21题第（Ⅱ）问边界值），猜测函数g（x）与h（x）单调性相反（函数值大（小）的函数单调递增（减）），通过单调性判断证实猜想.对于形式复杂的函数往往需要合理地拆分变形，然后利用导数判断单调性，通过中间变量传递过渡.如2014年高考全国卷Ⅰ理科第21题：设函数曲线y=f（x）在点（1，f（1））处的切线方程为y=e（x-1）+2.

（Ⅰ）求a，b；

（Ⅱ）证明：f（x）＞1.

通过“题在书外，根在书中”的压轴题的求解，给学生心灵以震撼.教师继续强化教材中基本结论的威力.

例4（第20题）已知O是△ABC所在平面内一点.

图5

图6

问题的本质是确定点O的位置，方法1根据向量的系数关系利用三角形中线定理，方法2、参考答案分别两次使用三点共线的向量式，利用数乘向量的定义及重心的性质.推广更为一般的问题：已知△ABC，点O满足，求△BOC，△OCA与△OAB的面积之比.

方法1：记f（a）=t，在同一坐标系下画出函数y=f（t）与y=|2t－1|的图像如图7所示，分别用粗线与细线表示，由图可知t≤1或t=2.画出函数t=f（x）的图像，如图8所示，由t≤ 1或t=2，可得

图7

图8

当0≤f（a）≤1时，2f（a）－1=2f（a）－1恒成立，即0≤f（a）≤1；

当f（a）＜0时，1－2f（a）=1－2f（a）恒成立，即f（a）＜0.

所以f（a）≤1或f（a）=2，以下同方法1.

方法1利用数形结合思想，从形的直观全局视角入手锁定目标，然后通过数的精准从局部角度解出结果，借助目标与条件的结构链及图中变量的“首尾相接”传递实现转化与化归；方法2根据分段函数的定义聚焦中间量f（a），灵活处理，巧妙过渡.本题若建构关于a的方程直接求解，过程相对繁杂.

例6（第19题）已知公差大于零的等差数列{an}的前n项和为Sn，且满足a1·a6=21，a2+a5=22.

（Ⅰ）若数列{bn}满足，求数列{bn}的通项公式；

（Ⅱ）证明：对一切正整数n，有b1+b2+…+bn＜1.

第（Ⅰ）问为已知数列{n2bn}的前n项和求通项公式，利用公式法求出通项公式要分类讨论，第（Ⅱ）问等价于，其放缩方式不唯一，如当n≥2时放缩幅度稍小，有放缩幅度再小一点，当n≥2时有也可由其几何意义（1·b1+1·b2+…+1·bn表示面积），利用积分求解：b1+众所周知，对于c（c为常数）的证明（少数情况为先求和再放缩）要保证同向可加性与和的有界性.本题的典型错误：b1+b2+…+，因为数列的前n项和是无界的（不收敛），又如，因为只对n=2，3，4有限项成立，尽管无穷递缩等比数列的前n项和有界，但指数函数的增长速度远远大于幂函数，无法保证加式的同向性.

三、教学感悟

试卷讲评课是一种重要的课型，尤其是复习阶段的主要课型.试卷讲评能对学生已学的知识起着矫正、巩固、充实、完善和深化的作用，是知识的再整理、再综合、再运用的过程，是师生共同探讨解题方法、寻找规律、提高解题能力的有效途径，还能促进师生反思教与学的不足，通过改进教与学的方法，提高教与学的效果.

当前试卷讲评的基本模式是“流水账”式就题论题地改错，教师不断讲，学生不停记，学生记完后反复浏览或识记正确答案甚至将笔记束之高阁，下次考试错误依旧.高耗低效现象的背后的深层原因是教师备课不到位，教师设计未能从学情（基础知识、基本经验、心理认知）出发做好“讲什么”与“怎么讲”.

1.试卷讲评内容要以学生基本经验为基础

柏拉图说：“天下本无新事.”我们要从旧中找出新，从新中辨出旧，只有如此才能学得深、理解得透.数学教学不能无视学生已有的知识经验，应当把学生原有的知识经验作为新知识的生长点，引导学生从原有的知识经验中，生长新的知识经验.

（1）教师要对试卷进行细致分析.

试卷是讲评的载体，教学的基本素材，对试卷的理解与把握关乎教学的成败.教师要细致准确分析试卷类型（如单元测试、期中（末）考试、高三月考等）、考试范围（班级考试、全市统考等）、考试目的（检测、选拔等）、试卷特点（试卷结构、命题特点等）、内容结构（知识点分布与要求）、目标水平结构（考试要求水平通常为了解、理解、应用等）.只有做到知己知彼才能百战不殆.如任课教师对试卷进行双向细目分析，（让学生）明晰高考对该内容的要求，避免学生不知深浅浪费宝贵的学习时间（提倡学有余力的学生拓展数学素养另当别论）；试卷重视数学思想（尤其是数形结合、化归与转化）、数学思维（用数学逻辑引导思考方向）的考查等.同时教师还要对近年来高考题做到胸有成竹，将试卷试题与高考真题进行比对分析，丰富其内涵.如第21题与2014年高考陕西卷理科第21题的区别与联系.

（2）教师要对学生错误给予正确分析.

学情是教学的基点，“讲什么”取决于教师对学生真实情况的诊断.通过对学生答卷的统计，如每道题学生的错误情况，每个学生的错误情况，产生错误的原因（审题错误、计算错误、逻辑错误等），发现学生对哪部分知识掌握较好（差），针对学生错误对症下药，切实做好查漏补缺、深化知识理解、体会数学思想方法、发展数学认知及元认知水平.如第2题学生采用的“直译法”更能对接教材对学生的要求，而灵活运用复数性质则需要学生在学习时加强探究；学生在第12题、第20题第（Ⅱ）问等题目出现对教材结论识记与理解不到位情况，导致无法找到解题的起点或行之不远.很多学生在第15题出现了用充分条件（由f（f（a））=|2f（a）－1|得f（a）≤1）代替充要条件的逻辑错误.教师要对学生的错误建立“错题本”，反思教师的原因，力争后面教学避免，同时给学生积极客观的评价（教师尽可能与学生同时独立完成试卷，比对自己与学生答卷的情况）.

2.试卷讲评方式要顺应学生心理发展需求

试卷的内容及处理方式等为学生所熟悉，若教师的教学方式依旧自然难以激起学生的兴趣，效果可想而知.反之，教师利用“不愤不启，不悱不发”，把话说到学生心坎里，根据学生的困惑与需求，实施针对性的教学，学生的兴趣与能力在不知不觉中得以提升.

（1）聚焦共性现象，关注个性发展.

课堂教学面对全体学生，因此教师选取问题势必具有共性.教师找到学生的通病和典型错误，找准其思维的薄弱点，有针对性地引导学生辨析，找准错因、错源，探究正确思路，力争纠正一例，预防一类，举一反三，触类旁通.对于个别学生的特殊错误，通过专门谈话给予个别辅导.

（2）追求通性通法，兼顾特殊技巧.

试卷讲评课应重视通性通法，加强数学知识的落实和数学思想方法的教学.通过通性通法，加深学生对知识、技能的理解和记忆，强化公式、法则的运用.注重通性通法的同时，不忘特殊情况下的（变形、设元等）技巧，让学生心中有模式而不囿于模式.通过关联，提高学生审题能力的同时有效规避学生处理问题的思维定式，初步实现“既见树木又见森林”.

（3）贵在体验过程，重在引导思考.

荷兰数学教育家弗赖登塔尔说过：“数学学习是一种活动，这种活动与游泳、骑自行车一样，不经过亲身体验，仅仅看书本、听讲解、观察他人的演示是学不会的.”“学之道在于悟”，只有学生亲身体验过的，才能获得属于他们自身的经验，才能实现迁移应用.苏联教育家巴班斯基认为：“教学效率不是决定于教师打算教给学生什么东西，而是决定于学生本身在课堂教学时间里掌握了什么东西.”［1］真正的教育应该是以学生的发展为本，这应该是最核心的教育理念［2］.试卷讲评不能因为时间紧，容量大就压缩学生体验、思考的空间，应尽可能发挥学生的主体作用.学生在试卷讲评前独立纠错，相互（纠）查错，课堂上学生汇报出错的原因、反思矫正策略方法及新的收获，教师相机而动，查缺补漏，引导学生构建知识网络，完善认知结构.通过学生之间的思维展示、相互补充、不断完善，使其思维的严密性、批判性、灵活性、深刻性和创造性得到大幅度的提升.

（4）适时适度拓展，归纳演练巩固.

试卷讲评往往安排在阶段复习检测之后，通过对新授课的反刍、章节的回顾、主线的梳理、试卷的诊断等，学生对知识、思想方法的理解不断向纵深发展，教师帮学生解惑、释疑、补缺的同时对相关内容进行拓展，对于出错率高的问题要及时变换角度出题，通过一题多变、一题多解、多题一解等方式使学生澄清错误认识，消除思维障碍，透过现象看本质.

教师对试卷的讲评具有针对性、层次性、新颖性、激励性，最大限度地暴露自己的思维过程，发挥教师的示范作用.但教学是一门科学，也是一门永无止境的艺术.授课教师试图通过一张“包罗万象”的试卷来包治百病是不现实的，多个看似到位的微专题致使试卷讲评的内容过多，占线过长（整张试卷评讲用三个课时），压迫式的课堂教学让“多重点”沦为“无重点”，导致后进生消化不良.

“教学活动要能拨动学生的心弦，调动学生的情感，激发学生学习的积极性．不是我教你学，也不是我启你发，而是教与学双方在教学活动中做到融洽的交流.教师引着学生走，学生反推着教师走，教师得心应手，学生如沐春风，双方都欲罢不能，其乐融融.”（刘国正语）通过优质高效的试卷讲评，定能使学生学会自主学习、合作交流、养成良好的反思习惯、发展思维能力、树立学好数学的信心，基础（知识、经验）自然获得，能力天然形成.

参考文献：

1.［苏］巴班斯基.论教学过程最优化［M］.吴文侃，等，译.北京：教育科学出版社，2001.

2．史宁中.数学教育的未来发展［J］.数学教学，2014 （1）.

3．郑良.探析命题特点明晰教学方向——2015年高考数学全国卷I试题评析及高三复习建议［J］.中学数学教学参考（上），2015（12）.

4.吴卫东.数学思维在“碰壁”中“自然成长”——一节高三复习课的启示［J］.中学数学（上），2015（11）.