非理想信道下的分布式认知多小区波束形成

张秀秀, 陈东华

(华侨大学 信息科学与工程学院， 福建 厦门 361021)



非理想信道下的分布式认知多小区波束形成

张秀秀, 陈东华

(华侨大学 信息科学与工程学院， 福建 厦门 361021)

摘要：针对非理想信道下的波束形成问题，将传统稳健波束形成设计推广至认知多小区，在认知干扰和认知用户速率约束下，构造基于最小化认知系统总功率准则的优化问题.通过半定松弛及S-Procedure算法将其转化为凸优化问题，并采用Primal分解将该凸优化问题分解为一组独立的子问题，从而实现了分布式求解,在降低复杂度的同时减少所需的反馈信息.仿真结果表明:算法不仅对信道误差稳健,而且收敛速度很快.

关键词：认知多小区； 分布式; 稳健波束； 凸优化

认知无线电技术[1]是解决频谱资源匮乏的有效手段，认知多小区网络充分利用现有网络频谱资源，极大提高频谱利用率.然而,目前关于认知多小区波束形成的研究还较少，而且大多假设信道状态信息已知，非理想信道信息下的研究则鲜见报道.由于时延、信道反馈等因素，在多小区中获取理想信道信息已经非常困难，在认知用户和主用户较少协作的认知网络中，认知小区获取到主用户的理想信道信息更不可行，因此，认知多小区稳健波束形成的研究尤为重要.在认知场景下,多小区稳健波束形成的算法多是集中式求解[2-5]，不仅复杂度高,而且还需大量反馈信息.Kim等[6]研究了非理想信道时的分布式稳健波束形成算法，但仅适用于每小区单用户情况.针对上述问题，将Pennanen等[7]的方法推广至认知多小区场景，提出了认知场景下的多小区稳健波束形成应用.认知多小区系统以各认知基站的最小发射功率为目标,在保证每个认知用户的服务质量(Qos)要求的同时，满足认知小区对主用户的干扰功率低于允许的干扰门限.干扰约束将小区间优化变量耦合在一起，从而使得优化问题成为非凸问题.本文采用半正定松弛(SDR)和Primal分解分布式求解这一非凸优化问题.

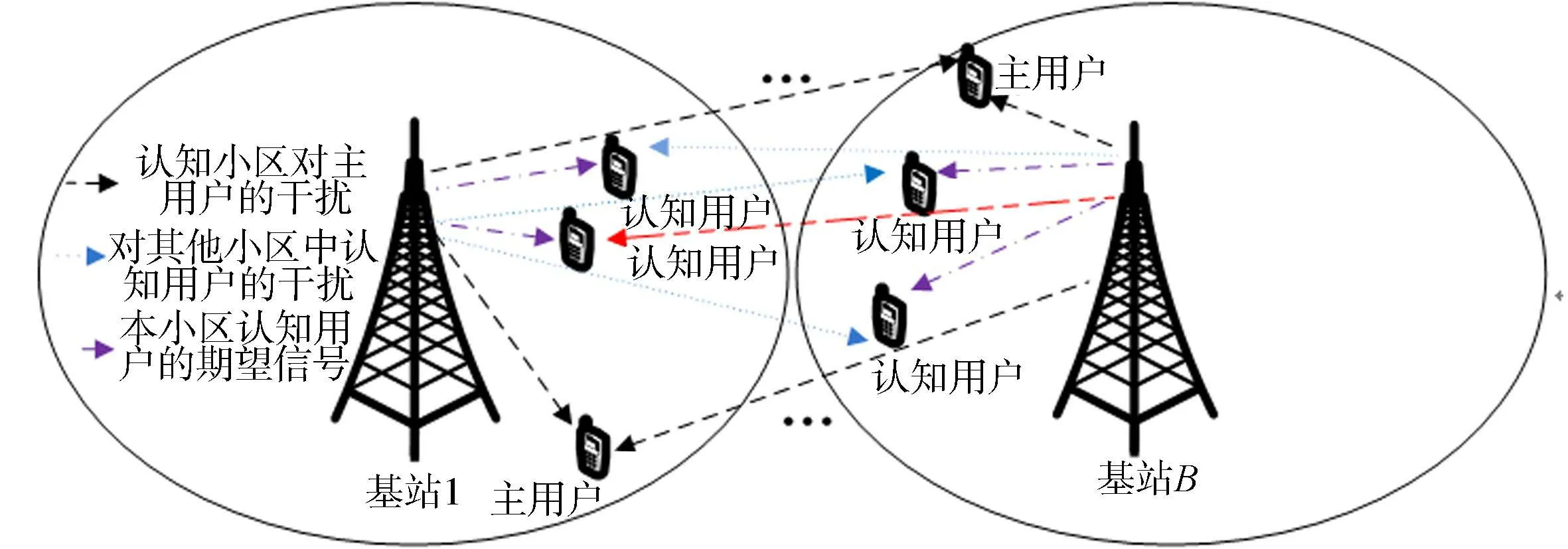
图1　认知多小区系统模型Fig.1　Cognitive multicell system model

1系统模型

认知小区b中第k个认知用户的接收信号为

(1)

式(1)中:mn,k∈CT×1为认知小区n中第k个认知用户的波束形成矢量;dn,k∈C为认知基站n发送给认知用户k的期望信号,且dn,k∈C满足E[|dn,k∈C|2]=1;zn,k为相应的加性高斯白噪声，且服从zn,k～CN(0,N0)分布;hn,b，k∈C1×T表示认知基站n到认知小区b中第k个认知用户的传输信道.

认知系统的发射功率为

(2)

认知小区n中第b个认知用户接收信号的信干噪比(RSN)为

(3)

对主用户的干扰约束为

(4)

式(4)中:gb,l∈C1×T表示认知小区b中的基站到认知小区l中主用户的传输信道矢量.

2稳健波束形成

2.1稳健认知多小区波束形成

在实际应用中，由于信道估计误差等因素，每个认知基站都不可能获得理想信道状态信息.认知基站n到认知基站b中第k个认知用户的传输信道为

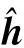
在信道误差及最差性能准则下，化模型为

(5a)

(5b)

(5c)

由于误差取值的连续性，式(5b),(5c)包含无穷多个误差，为了解决无穷多约束问题,采用S-Procedure[8]将其转换为LMI(linearmatrixinequality)形式[7],与约束式(5b)等效的LMI为

同理，与约束(5c)等效的LMI为

(8a)

(8b)

(8c)

(8d)

(8e)

(8f)

松弛秩1约束，则上式为标准的半正定规划问题，从而可用数值算法或凸优化软件如CVX[9]求解.

2.2分布式稳健波束形成算法

优化问题(5)需要集中方式求解，从而增大实现复杂度和信令开销.文献[7]在传统多小区场景下提出了分布式稳健波束形成方法,下面将文献[7]的分布式处理方式推广到认知场景，从而实现分布式求解.式(8)中不同认知基站的波束形成矢量通过干扰约束耦合在一起，采用Primal分解方法[10]将耦合的干扰约束解耦，从而把优化问题(8)分解成一个主问题和B个子问题.分解后的子问题为如下半正定规划问题,即

(9a)

(9b)

(9c)

(9d)

(9e)

(10)

主问题通过更新耦合变量χb和Pb来控制子问题的更新，χb和Pb可由投影次梯度法更新，即

(11)

(12)

如果耦合的认知基站间通过反馈信息允许次梯度交换，则对于∀b∈B，认知基站b可独立更新，从而实现了各基站独自求解优化矢量.

3仿真结果分析

认知系统包含B=2个认知小区，每个认知基站配置T=4副发射天线，每个小区包含K=2个单天线认知用户及1个单天线主用户.认知基站与每个用户间的路径损耗为0dB，即路径增益与噪声的比值为1.为不失一般性，假设

σ和χ(t)的取值将在仿真中给出,信道矢量为零均值、单位方差的复高斯随机变量，即信道服从瑞利衰落.为简化起见，假设信道误差满足

在不同迭代步长、不同干扰温度下,归一化次优性随迭代次数的变化曲线,如图2所示.归一化次优性定义为

上式中: P(t),Pc分别表示分布式算法中t次迭代后的总功率和、采用集中式算法的总功率.

图2　不同参数下分布式算法的收敛曲线Fig.2　Convergence curves of distributed algorithm with different parameters

图2中：γ=0dB；χ(0)=0.25；ε=0.01.不同参数下分布式算法的收敛曲线，如图2所示.由图2可知:减小干扰温度或减小迭代步长，分布式算法的收敛性都会变慢.这是由于步长越长越易接近收敛条件；干扰温度越大收敛条件越易满足.

不同信道误差下，系统消耗的总功率随认知用户信干噪比(RSN)门限变化的曲线，如图3所示.由图3可知:随着用户RSN的增加,系统所需的总功率也随之增加;分布式算法的消耗总功率性能和集中式算法的消耗总功率基本相同，并且信道误差越小,系统总功率越接近理想信道下系统的总功率.

不同信道误差下,系统和速率随认知用户信干噪比RSN门限的变化曲线，如图4所示.由图4可知:系统和速率随着认知用户RSN的增大逐渐增加；理想信道下的系统和速率为基站所能达到的系统和速率的上界，而且信道误差越小,基站所获得的和速率越接近该上界,但在实际中很难获得精确的信道信息.

图3　系统总功率与认知用户信干噪比RSN门限的关系　　图4　系统和速率随认知用户RSN门限的变化曲线Fig.3　Total transmit power versus RSN threshold　　　　　Fig.4　Sum-rate versus RSN threshold

4结束语

在认知用户和主用户较少协作的认知网络中，系统很难获得理想的信道信息，认知多小区中的稳健波束形成是实际应用中必须考虑的问题.依据最小化功率优化准则，联合设计了认知多小区稳健波束形成矢量，并分布式实现了该优化问题.相比集中式处理方式，分布式算法只需每个基站得到本小区用户的局部信道状态信息，基站间的协作信息可在基站间直接进行而不再需要中心控制单元，从而降低复杂度和反馈开销.仿真结果表明：在不同参数下，文中算法不仅对信道误差稳健，而且经少量次数迭代后十分接近集中式算法的性能.

参考文献：

[1]HAYKIN S.Cognitive radio: Brain-empowered wireless communications[J].Journal on Selected Areas in Communications,2005,23(2):201-220.

[2]GHARAVOL E A,LIANG Y C,MOUTHAAN K.Robust downlink beamforming in multiuser MISO cognitive radio networks with imperfect channel-state informing[J].Transactions on VEHICULAR,2010,59(6):2852-2860.

[3]DU Huiqin,RATNARAJAH T,PESAVENTO M,et al.Joint transceiver beamforming in MIMO cognitive radio network via secondorder cone programming[J].Transactions on Signal Processing,2012,60(2):781-792.

[4]WIJEWARDHANA U L,CODREANU M,LATVA-AHO M.Robust beamformer design for underlay cognitive radio network using worst case optimization[C]∥On International Symposium and Workshops on Modeling and Optimization in Mobile, Ad-Hoc and Wireless Networks.Tsukuba Science:IEEE Press,2013:404-411.

[5]PONUKUMATI D,GAO Fei-fei,BODE M,et al.Robust coordinated downlink beamforming for multicell-cognitive radio networks[C]∥IEEE 24th International Symposium on Personal Indoor and Mobile Radio Communications (PIMRC).London：International Conference on Communications，2013:719-723.

[6]KIM Y J,SONG M G,CHO Y S,et al.Decentralized beamformer design with limited multi-cell cooperation for interference channel of cognitive radio networks[J].Transactions on Wireless Communicaions,2013,12(8):4142-4152.

[7]PENNANEN H,TOLLI A,LATVA-AHO M.Decentralized robust beamforming for coordin-ated multi-cell MISO networks[J].Signal Processing Letters,2014,21(3):334-338.

[8]BOYD S,VANDENBERGHE L.Convex optimization[M].Cambridge:Cambridge University Press,2004:655-656.

[9]GRANT M,BOYD S.CVX:Matlab software for disciplined convex programming,version 1.21[EB/OL][2011-01-04].http:∥cvxr.com/cvx.

[10]PALOMAR D P,CHIANG M.A tutorial on decomposition methods for network utility maximization[J].IEEE Journal on Selecten Areas in Communications,2006,24(8):1439-1451.

(责任编辑： 陈志贤英文审校： 吴逢铁)

Beam Forming of the Distributed Cognitive Multi-Cell System for Imperfect Channel

ZHANG Xiuxiu， CHEN Donghua

(College of Information Science and Engineering, Huaqiao University, Xiamen 361021, China)

Abstract：To solve the beam forming problem for imperfect channel, the robust beam forming design method for conventional system is extended to cognitive multi-cell system. Under the constraints of cognitive interference and cognitive users′ rate, the optimization problem is formulated based on the criterion of minimization of cognitive system′s total power. The problem is converted to a convex optimization problem by means of semi-definite relaxation and S-Procedure algorithm, and is decomposed into a group of independent sub-problems by using Primal decomposition. So then a distributed solution is achieved and both computational complexity and required feedback information are reduced. Simulation results show that the algorithm is not only robust to channel errors but also convergences quickly.

Keywords：cognitive multi-cell; distributed; robust beam forming; convex optimization

中图分类号：TN 929.5

文献标志码：A

基金项目：福建省自然科学基金资助项目(2012J05119)

通信作者：陈东华(1977-)，男，副教授，博士，主要从事宽带无线通信及无线网络资源管理方面的研究.E-mail:dhchen@hqu.edu.cn.

收稿日期：2014-09-09

doi:10.11830/ISSN.1000-5013.2016.02.0185

文章编号：1000-5013(2016)02-0185-05