按数控技术专业需求进行《高等数学》课程改革的探索与研究
陈雪
【摘 要】高等职业教育的培养模式必须以“职业”为基础,以“能力”为本位,培养目标必须根据不同的职业岗位的具体要求来确定。本立项结合数控技术专业培养需求,以培养数控技术应用能力为主线,以“应用”为主旨设置课程,构建自己的课程体系,增强实用性和针对性,以“必需”、“够用”为原则,通过讲清基本概念,使之掌握分析问题的思路和方法。
【关键词】专业需求;实用性;课程改革;探索
现阶段高职教育体系中,高等数学是一门重要的基础课。国内在高职高等数学教学改革的趋势上,提出了完全融入专业教学的思想。将传统意义上高等数学教育的文化性、基础性、工具性的教育方针,改革为适应职业教育的特点,因需施教,理论上适度,专业上够用;基于工作过程,不追求大而全,突出数学工具性、方法性的特征。作为我院重点建设专业之一的机械工程系在不断发展的同时,对于专业基础课的需求也在不断更新。而如果高等数学仍然以单纯理论教学方式进行教学,既加大了教与学的难度,同时也不能满足专业发展需要。
为此我们着力探索如何充分发挥高职数学教学的科学价值和人文价值,不断适应专业课发展需求,实现传授数学知识与提升数学素养的双重目标,重点开展了如下研究工作:
1 充分了解学生学情
完成了对数控技术专业学生数学学习情况的调查,包括入学新生数学基础知识的调查,正在学习数学的学生、毕业班学生数学知识状况的调查,并对这三类调查的结果进行具体分析。随着高职院校招生规模的不断增加,生源质量也在逐年下降,新生的数学基础极其薄弱,2011年不少省份的高职录取最低线已跌至200分。面对这样的状况,高职数学课程下一步该如何走,如何取得最大限度的教学效果成了亟待解决的问题。
2 强化高等数学的实用性
为提高学生“用数学”的能力,在教学内容中尝试增加简单的数学建模、数学实验等实践性教学环节。期间为确保提高学生的积极性,引导学生主动学习“用数学”,在教学内容安排上,我们以“案例”教学为主,选题尽量紧贴现实生产和生活,使学生从中不断地感受数学在现实中的应用。同时,还引入了数学建模的初步思想,精选了近几年来全国大学生数学建模竞赛中的典型例题,使学生了解当代数学建模的发展和它在社会生产建设中的作用。
针对教学现状中存在的问题,进行了影响教学质量的因素分析,提出课程教学改革的对策和实施方案。
3 根据数控专业需求更新教学内容
随着制造业技术的发展及工业生产与民用需求的不断增加,数控技术的应用已越来越受到制造业的青睐,如航天、汽车、家用电器等行业。我们结合近几年的数控教学实践,对数控技术中应用到的一些典型数学知识做了深入的探究。
3.1 数控技术中“坐标系”的应用
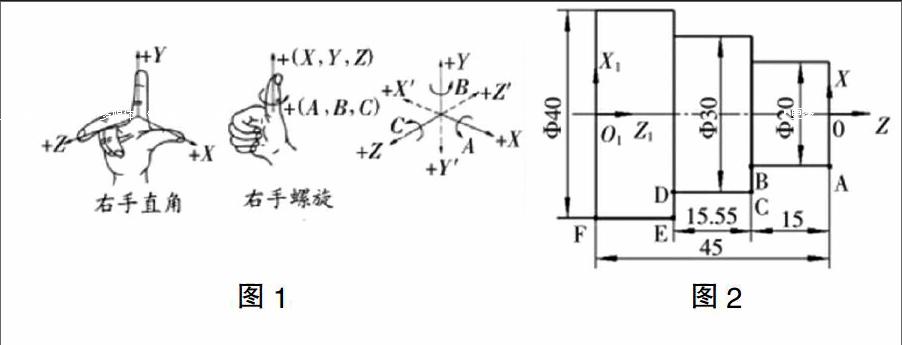
数学中的坐标系为数控编程指明了方向,建立编程坐标系,将会为数控编程加工带来极大的方便。工件在数控机床上的加工,是通过刀具与工件的相对运动来实现的,机床的运作由数控系统发出的指令来控制,为了定量地描述数控机床上刀具相对工件的运动位置,就必须建立机床加工用的坐标系。根据ISO841标准,数控机床坐标系用右手笛卡儿坐标系作为标准确定。坐标系方向如图1所示。
以图2为例,图中建立了两个坐标系,最简单的原则是看用哪个坐标系编程比较方便,计算工作量少,一般选择工艺基准与设计基准相统一的原则,从图中可以看出,径向的设计基准为轴心线,轴向的设计基准为右端面,因此应选择 XOZ 为编程的坐标系。
3.2 数控技术中“三角函数”的应用
三角函数在数学中属于初等函数。在数控中运用到的三角函数一般比较简单,但对于有些数学基础较差的学生来说成了拦路虎,因此正确引导学生运用数学知识解决数控问题,会让一些原先感觉学习数学无用的同学认识到数学知识的重要性,增强了学生的学习动力。
3.3 微积分学的创立,极大地推动了数学的发展,过去很多初等数学束手无策的问题,运用微积分往往迎刃而解,也显示了微积分学的非凡威力。微积分是与应用联系着发展起来的,最初牛顿应用微积分学及微分方程推导出了开普勒行星运动三定律。此后,微积分学极大的推动了数学的发展,同时也极大的推动了天文学、力学、物理学、化学、生物学、工程学、经济学等自然科学、社会科学及应用科学各个分支的发展,并在这些学科中有越来越广泛的应用。
4 结合学生需要更新教学方法
探索新的高职数学教学方法,加强现代教育技术在高职数学教学中的应用。各种媒体的数学教学资源,如何整合、衔接现代教育教学技术,如何才能跟得上计算机信息技术的发展,传统的教育教学方法如何改革等都是值得我们研究的课题。具体做法是:
4.1 引入案例教学方法
从专业案例入手,把理论和实训中遇到的数学问题引入教案,我们发现数控专业在实操中应用最多的是三角函数,在几乎所有的零件图中,需要确定点的位置时运用的都是三角函数。因此我们做了大胆的改变,把三角函数重又增补进教案里,再把它与高数结合,这样的讲解学生既不会觉得生疏又容易理解。
此外,还多方面向学生介绍在本专业有实用价值的数学模型。一些专业教材中,如《机械制造基础》的问题都是现实中存在又必须解决的问题,正是数学建模教学的最佳素材。如在讲授曲率时可穿插“确定磨削零件表面的砂轮直径”的实例,使学生在学习《数控加工技术》等课程时更得心应手。
4.2 强化逻辑思维能力训练
为了提高学生对数学的学习兴趣,发现数学之美,我们设计一些日常生活中的数学问题和逻辑思维题放在每节课的课前。比如黄金分割,千百年来以一种非常神奇的方式广泛地应用到我们生活中的各个领域,如植物的叶子,我们从某种植物的顶端往下看,如果每层叶子只画一片来表示。第一层和第二层的相邻两叶之间的角度差约为137.5°,若我们想到一周为360°,那么137.5°:(360°-137.5°)=0.618。也就是说,各种植物叶子的生长规律中自然隐藏着黄金数。据植物学家研究,这种叶片角度对通风与采光都是最好的。
5 建立科学的考核方式
注重培养学生的应用能力,改革课程考核方式,有针对性的进行教学方法改革。数学课教学不仅要向学生传授知识,更重要的是要培养学生的应用能力,而要实现这一根本性目标,科学、合理的评价方式是基础和关键。从2010年开始,我们对数学课程的考核进行了改革,改变了过去完全以笔试为考核方式的传统做法,采取“6:2:2”综合性的考核方式,即考核由笔试成绩+学习态度+问题解决。其中笔试考查学生对基本知识掌握情况,占60%;学习态度包括平时作业、课堂出勤、课堂表现等综合评定,占20%;问题解决考核学生实际应用和解决问题的能力,占20%。
6 效果评价与特色创新
本项教学改革自立项,已经过一年的实施,效果非常显著对12级数控2班进行小范围试验,在第一学期中,前半学期用原有的教学内容和方法,后半学期采用新的教案和方法。结果表明,该班期中平均分为69.92,及格率为87%,期末平均分为76.73,及格率为96%,两项结果均有提高。据评教调查表统计,三年来学生对数学课程的评优率均在90%以上。再次,学生对数学课程的掌握程度普遍提高,受到后继课程教师的好评。
【参考文献】
[1]云连英.面向专业需求的高职数学课程设置研究[J].数学教育学报,2008,8(4):73-76.
[2]杜吉佩,等.高等职业教育数学教学内容的调查与分析[J].辽宁高职学报,2004,2.
[3]兰永胜.数学思想方法与建模技巧[M].青岛海洋大学出版社.
[4]乐经良.数学实验[M].高等教育出版社.
[5]微积分(Calculus)(英文版)[M].[美]Dale Varberg,Edwin J.Purcell,Steven E.Rigdon.机械工业出版社.
[责任编辑:杨玉洁]

