基在“探究与发现”教学中教师该做些什么

冯斌

摘 要：“探究与发现”课的教学目标定位是什么？从教师“教”的角度思考”该“教什么”？“怎么教”？本文作者在这些方面做了些探索与实践，也得到了同行与专家们的认同. 本文以人教版选修2-3第一章中的拓展性栏目“探究与发现：‘杨辉三角中的一些秘密”一课为例，从教师“教”的角度与同行们交流一下这节知识拓展类选修课磨课过程中的所思所为.

关键词：探究与发现；教什么；怎么教

背景：两年一次的浙江省课堂教学评比活动在温州中学举行，本次评比活动的主题为：深化课改背景下的“高中数学教学模式变革”——知识拓展类选修课程教学研究，宁波的指定课题为人教版选修2-3第一章中的拓展性栏目“探究与发现：‘杨辉三角中的一些秘密”，并取得了第一名的佳绩，笔者有幸在“浙江省疑难问题解决培训”活动中做了点评. 本节课还代表浙江省参加了“第六届全国高中青年数学教师优质课观摩与评比”活动，并荣获了大会最优秀奖. 成绩的背后离不开参赛选手宁波市鄞州区正始中学陈碧文老师自身的努力，更凝聚了专家团队的集体智慧. 知识拓展类选修课程作为省级比赛课内容在我省属于第一次，而且也没有可以借鉴的资料，本文旨在从教师“教”的角度与同行们交流一下这节知识拓展类选修课磨课过程中我们的所思所为.

我们的思考

数学知识拓展类选修课程旨在改变学生以单纯地接受教师传授知识为主的学习方式，是以学生动手动脑，通过自主探索、合作交流为主要学习方式的学习研究活动. 从教师“教”的角度来讲，我们思考的问题是教师该“教什么”与“怎么教”.

1. “教什么”的思考

课堂教学首先要考虑的是“教什么”的问题，即教学目标定位的科学性与合理性. 人教社章建跃老师的三个理解，即“理解教材、理解学生、理解教学”是解决“教什么”的制胜法宝. 通过对教材、学生、教学三方面的分析确定如下教学目标、教学重点、教学难点.

【教学目标】

从不同的角度，研究杨辉三角中所蕴含的规律，并用组合数表示；通过杨辉三角的研究，总结归纳出杨辉三角的研究方法，并拓展为对一般数阵的研究方法. 通过自主探究与合作交流，养成观察问题、发现问题、提出问题、探究问题、解决问题的学习习惯，以及勇于批判、敢于创新的精神.

【教学重点】

通过不同的角度研究得到杨辉三角的性质，并最终总结出一般数阵的研究方法.

【教学难点】

将杨辉三角的规律用组合数表示.

2. “怎么教”的思考

作为非高考内容的数学知识拓展类选修课，又是选自“探究与发现”栏目，课堂教学的模式是探究式教学，《普通高中数学课程标准》明确指出：“数学探究是指学生围绕某个数学问题，自主探究、学习的过程. 这个过程包括：观察分析数学事实，提出有意义的数学问题，猜想、探究适当的数学结论或规律，给出解析或证明.” 探究学习充分体现了“以生为本”、“学为中心”的教学理念，让学生不但学会，更重要的是会学、乐学. 那么，在学生探究与发现“杨辉三角 ”中的一些秘密过程中教师该做些什么呢，笔者认为可围绕以下关键词：引导、组织、帮助、提升.

引导：即导趣、导向、导法. 探究课题的引入力求激发学生的学习与探究的兴趣，进而教学生如何观察问题、发现问题、提出问题，明确探究的任务，课题的探究过程中引导探究方向，引导学生掌握数学研究的一般方法，使学生积累数学的基本活动经验（包括实践操作经验与思维活动经验）.

组织：搭建探究平台，组织探究形式、明确探究任务，控制探究时间，提供展示平台，并对巡视中发现的问题及时调整.

帮助：帮助学生明确探究的方向、策略，帮助学生纠正探究中的错误、解析疑点、评析难点.

提升：不同思路方法的提炼，让学生感悟研究问题的思想方法、解决问题的策略，方法的优化等.

课例的打磨点滴

本节课从试教到正式比赛历时6个月，经过几番打磨，形成如下共识.

1. 引入探究课题

课题引入围绕“聚神、激趣、点题、启思”八字方针. 本节课通过简要讲解有关河图、洛书的历史知识引出数阵的概念，通过数阵的概念引出杨辉三角，提出本节课的研究课题“探究与发现‘杨辉三角中的一些秘密”. 通过这个引入环节，旨在体现数学的文化价值，激发学生的学习兴趣，不仅引出研究课题，而且为后续探究其他数阵做好铺垫.

2. 搭建探究平台

（1）构建知识平台

让学生回顾已经学习过的杨辉三角的性质，构建共同基础，提供知识平台.

教学片断一：知识回顾环节

教师：杨辉三角在我们学习二项式系数的性质时已经有所接触. 那么，我们已经学习过杨辉三角的哪些性质呢？我请一位同学来回答一下.

学生1：杨辉三角中每一个数都是二项式系数.

教师：贾宪在他的《开方作法本源图》中写道：“左衺乃积数，右衺乃隅算，中藏者皆廉”. 用今天的话来讲，就是说杨辉三角中的每一个数都是二项式系数，而二项式系数都可以写成组合数. 从而我们就可以把杨辉三角写成以下的形式（课前已板书），其中第n行第r个数可以写成an，r=C，这对我们今天的研究非常重要.

教师：还有吗？

学生2：杨辉三角中每一个数都是两肩上数之和.

教师：非常好！杨辉三角中每一个数都是两肩上数之和，用组合数表示就是：

C+C=C，这个结论最早是由南宋时期的杨辉所发现的，所以称之为杨辉恒等式.

还有其他性质吗？

学生3：杨辉三角每一行数字之和是2的n次.

教师：很好，杨辉三角每一行之和为2n，用组合数来表示就是：

C+C+C+…+C+…+C+C=2n.

学生4：杨辉三角是左右对称的：C=C.

教师：以上几个性质，是我们已经知道的. 接下来我们就要研究一下杨辉三角的其他性质了.

（2）提供导学案

为便于探究活动，教师给学生提供了导学案，内容包括：

①阅读材料：杨辉三角的历史

②搭建探究活动的支架：回顾杨辉三角；初探杨辉三角（提供了两个杨辉三角：用数字表示的杨辉三角，用组合数表示的杨辉三角）；再探杨辉三角（提示：将杨辉三角摆放成直角三角形，谈谈你们组的发现）；三探杨辉三角（提示：将杨辉三角中的奇数涂黑，又会有怎样的发现）；小结与收获（通过本节课，你对数阵的研究有什么心得）；课后探索（查找资料，并阅读华罗庚的《从杨辉三角说起》，看看杨辉三角中还有哪些我们没发现的秘密；用我们今天所学的探究方法，研究莱布尼茨三角，你能从个数阵中发现哪些秘密呢）.

（3）提供技术支持

为便于学生展示探究成果，教师在课堂上借用了多媒体“交互式电子白板”.

3. 指明探究方向

“杨辉三角”中有很多秘密，有许多数学家都研究过，华罗庚先生在1964年2月就出版过《从杨辉三角谈起》一书，教材内容只是“杨辉三角”秘密中的冰山一角. 一节课中对内容的广度与深度把握非常关键，本节课对内容的取舍原则是在学生现有的知识与经验的基础上，运用“最近发展区”理论对内容进行取舍：引导学生从二项式系数出发，联想已学的组合数公式“C=C、C+C=C”，类比数列的有关问题如“通项、递推、求和”，及从函数的角度去探究“杨辉三角”中的秘密.

4. 组织探究活动

“自主、合作、交流”是新课程标准下倡导的一个学生重要的学习方式，已被一线教师们接受和采纳，但要避免假探究. 本节课根据学生的学情采用的是教师引导下的学生自主探究与合作交流相结合的探究方式，4人一小组，探究活动的流程：独立思考—小组合作—展示成果—师生互动—总结提升，其中“独立思考”与“小组合作”时间大概15分钟左右.

5. 引导探究策略

教师的引导主要让学生体会研究数阵的方法：取数的方法、研究的内容、研究的方法.

（1）取数的方法（“形”的角度）：①借鉴苏轼的《题西林壁》，从“横看”、“侧看”（45°，30°）、“整体” 、“局部”等四个角度取数. ②改变杨辉三角的摆放形状，如变“等腰三角形”为“直角三角形”等.

（2）研究的内容（“数”的角度）：①类比数列的有关问题，如“通项、递推、求和”. ②联想特殊的数列，如高阶等差数列、斐波那契数列等. ③联系函数的性质，如，“对称性”、“奇偶性”、“增减性”、“最值”等.

（3）研究的方法：为降低探究难度，提高学习兴趣，根据学情教师提出要求：“用数字表示的杨辉三角寻找规律，用组合数表示的杨辉三角总结和论证规律”，学生采取：“观察—归纳—猜想—验证—证明”的探究问题步骤，合情推理与演绎推理相结合. 同时教师还渗透实事求是的科学态度，提醒学生猜想不一定正确，如学生猜想的结论“第n项看做一个数，猜想这个数是11n-1”是错误的.

6. 展示探究成果

由于课堂时间的限制，教师通过巡视，有选择地挑选几个组上台展示探究成果，并追问探究的思路.

教学片断二：小组成果展示环节

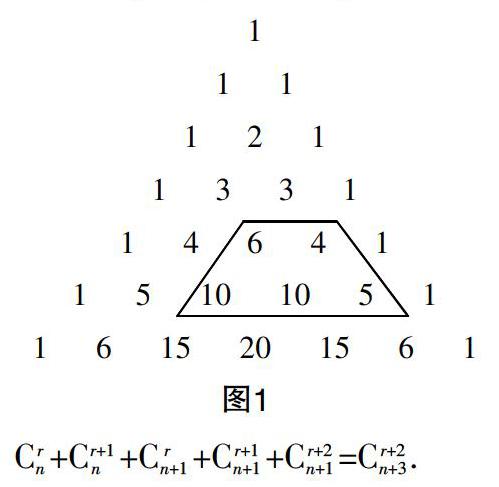
（第一组）学生1：将梯形中5个数相加就是下面隔行的数（如图1）.

C+C+C+C+C=C.

思路：因为杨辉三角的每一个数都是肩上两数之和，我们就在想，是不是可以进一步向上推导？

教师：从已知的结论中挖掘出新的内容，非常好！

（第二组）学生2：我们组发现每一斜行前n个数加起来都是下面一行的第n个数

C+C+C+C+…+C=C.

推导到一般情形：C+C+C+…+C=C（n>r）.

思路：我们是从求和的角度来研究的，既然横的一行相加存在规律，那么斜的一行相加看是不是也可以得到一些结论？

教师：采用类比方法进行研究，类比是研究数学问题的常用方法之一.

（第三组）学生3：杨辉三角中每一行数的平方和都是杨辉三角中的数

（C）2+（C）2+…+（C）2=C.

思路：既然杨辉三角每一行的和存在规律，那么每一行的平方和是不是也有规律呢？

（第四组）学生4：将杨辉三角30°角斜行加起来得到数列1，1，2，3，5，8，13， 21，34，55，89，144，…每一项都是前两项之和.

思路：通过教科书上的提示得到的.

教师：查找资料也是一种非常好的学习方式，这个数列恰好是斐波那契数列.

（第五组）学生5：我们发现单纯用数字的角度去看的话，每一行都是11的次数幂.第一行11的0次幂，第二行11的1次幂，第三行121是11的2次幂，我们验算了一下，11的3次幂正好是第四行1331，因此我们猜测将杨辉三角第n行数字依次写下来是11的n-1次幂.

教师：11的1次幂为11，11的2次幂为121，11的3次幂为1331，好像确实是这样.那么我们一起来帮他们验算一下11的4次幂.

学生众：14641.

教师：11的5次幂是多少呢？

学生众：11的5次幂为161051.

教师：太可惜了，这是一个多么美好的结论啊，问题出在哪儿呢？我们一起来看一下，同学们，我们11的4次幂是如何计算的啊？我们是通过1331×11计算得到的. 从这里我们会发现，14641其实是两个1331错位相加得到的. 那么11的5次幂是不是也是由两个14641错位相加得到？而在这个过程中，出现了一个问题，大家发现了没有？

学生众：进位了！

教师：非常好. 产生了进位就会出现问题，所以我们是不是只需要把这个结论改一改，将杨辉三角中每一行数字错一位叠加所得到的结果是11的若干次方.

其实我们在研究过程中，不要被自己的惯有思维所约束，比如，我们可以从数的奇偶性角度去研究数：

①当我将杨辉三角中的奇数涂黑.大家看，是不是会得到一个有趣的图形？其中第2的k次行均为奇数，奇数行的下面一行除两端之外均为偶数.

②将杨辉三角中的奇数用线段连接起来，就可以得到一个有趣的三角形——谢尔宾斯基三角，对谢尔宾斯基三角进行拓展，得到：谢尔宾斯基塔、谢尔宾斯基地毯、谢尔宾斯基海绵，我们就诞生了一门新的数学分支——分形数学. （多媒体展示优美图案）

又比如，我们为什么一定要把杨辉三角放成等边三角的形式呢？有些人就不这么认为，他把杨辉三角摆放成直角三角，也得到了一些有趣的结论，留给同学们课后探究.

7. 总结探究收获

本环节通过教师的引导，让学生从知识与方法两个侧面总结本节课的收获，并由教师做必要补充.

教学片断三：总结提升环节

教师：接下来，我们来总结一下.通过这节课，你收获了些什么？

学生1：通过这节课的研究，我们发现了杨辉三角的很多秘密. 比如，杨辉三角每一斜行都是一个特殊的数列（高阶等差数列），并且这些数列的和又是下一行中的数. 杨辉三角每一横行的平方和也是杨辉三角中的数. 通过30°的斜行求和，还可以得到斐波那契数列.

教师：总结得很好！当然，我们这节课不仅仅是研究杨辉三角，我们更需要通过对杨辉三角的研究，学会对数阵的研究方式. 那么通过这节课，你们对数阵的研究又有哪些心得呢？

学生2：从杨辉三角的研究中，我发现数阵可以从横的、斜的、竖的这几个角度去看，也可以局部看、整体看.

学生3：从杨辉三角的研究中，得到数阵研究的内容可以类比数列，从通项、递推、求和这几方面入手.

教师：很好！我们发现可以从横看、侧看、竖看这几个角度去研究数阵. 既然数阵与数列的概念如此相似，我们也可以借鉴数列的研究内容，从数阵中的通项、递推、求和，以及数阵中所蕴含的特殊数列这几个角度来研究数阵.

教师：通过今天的研究，我们已经把杨辉三角的秘密都找到了吗？（学生：没有）当然没有，我在课堂的开始就讲过，贾宪用它手算高次方根，那么它是如何计算的呢？牛顿的微积分与它有一定的关联，关联在哪呢？我希望大家课后查找资料，并阅读华罗庚先生的《从杨辉三角说起》，去寻找这些答案，看看杨辉三角中还有哪些我们没发现的秘密. 有兴趣的同学还可以运用我们今天所学的探究方法，研究莱布尼茨三角，你能从个数阵中发现哪些秘密呢？

当然，教学过程的打磨还包括板书设计、时间分配、视频制作等，这里就不一一赘述了.