非线性主成分分析和R B F神经网络的电力系统负荷预测

刘晓菲，商立群（西安科技大学电气与控制工程学院，陕西西安　710054）



非线性主成分分析和R B F神经网络的电力系统负荷预测

刘晓菲，商立群
（西安科技大学电气与控制工程学院，陕西西安710054）

KEY W0RDS：Power system；non1inear PrinciPa1 comPonent ana1ysis；RBF neura1 network；re1evance；1oad forecasting

摘要：电力系统负荷预测是电力系统规划与运行的重要内容，为提高负荷预测的精度，针对主成分分析法在涉及到多指标预测体系中降维作用不明显，且考虑不到指标间非线性关系的问题，采用非线性主成分分析法改进RBF神经网络输入量，该方法克服了数据之间相关性的约束，进一步降低了预测指标维数，兼顾了指标间非线性关系，保留了原始数据的足够信息，获得电力系统负荷预测的主成分，显著地减少了径向基函数神经网络的输入量，从而提高了电力系统负荷预测的精度。实例分析验证了该方法的有效性。

关键词：电力系统；非线性主成分分析；RBF神经网络；相关性；负荷预测

电力系统负荷预测是指对未来某特定时刻的电力系统负荷数值进行预测，它是电力系统科学规划和经济运行的重要组成部分，也是电力系统经济调度中的重要内容[1-2]。准确的负荷预测，可以合理地安排电网设备的运行与维护，维持电网的稳定性，从而保证社会正常的生产和生活。

径向基函数（radia1 based function）神经网络是20世纪90年代由Moody和Darken提出的，它属于前向神经网络类型，能够以任意精度逼近任意连续函数，具有很强的泛化能力，学习速度快，并且相对于传统神经网络而言，它具有更快的收敛速度和更强的鲁棒性[3-4]。但是，径向基函数神经网络要求输入样本只能有适当的重叠，否则神经元不能做出有效的响应。而电力系统负荷预测受经济、政策、社会等指标的影响，且这些指标之间的相关性比较强，即存在高重叠的一些指标，如果直接运用RBF神经网络进行预测，则难以得到满意的结果。针对这一问题，通过主成分分析法降低各指标的相关性是一种有效的解决方法[5-7]。文献[8]采用主成分分析方法重构原输入空间，降低了指标的相关性，然后根据各主成分的贡献率来确定网络结构，进而有效解决了预测精度下降的问题；文献[9]运用主成分分析法对原始数据进行处理，将选取的主成分作为神经网络的输入量，既减少了输入量的维数，又降低了各输入量的相关性，提高了神经网络的收敛性和稳定性；文献[10]建立了基于主成分前向反馈神经网络的输出功率预测模型，经主成分分析后，消除了神经网络输入样本的相关性，简化了网络结构，提高了网络的收敛速度，进而提高了预测精度。

主成分分析法具有浓缩信息，降低指标维数，简化指标网络结构等特点。然而当原始指标的个数较多时，第一主成分的贡献率往往较低，主成分分析法起不到很好的降维作用，且此时原始指标之间多为非线性关系，若继续采用主成分分析法，存在被忽略的主成分往往包含有原始数据重要的非线性信息，会造成大量的信息丢失，效果难以令人满意。本文采用非线性主成分分析[11-12]，对原始指标进行对数中心化处理，然后将得到的主成分作为径向基函数（RBF）神经网络的输入，提高电力系统负荷预测的精度。

1　主成分分析及改进

主成分分析是一种考察多个指标间相关性的多元统计方法[13-14]，通过降维的方式，用少数几个主成分代替原有的多个指标，使它们尽可能多地保留原始指标的信息，且彼此间互不相关。

1.1主成分分析的一般步骤

1）设有n个样品，每一个样品有p个观测指标，分别用X1，X2，…，Xp表示，得到原始数据矩阵为其中χiJ为第i个样本的第J个指标的观测值，而通过主成分分析法确定的新的指标为Y1，Y2，…，Ym（m≤p）。

4）求出Zi＝［zi1，zi2，…，zip］T的m个主成分分量为

5）求出由m个主成分生成的线性加权综合评价函数为

1.2主成分分析的改进

主成分分析是一种线性降维技术，该方法对原始数据进行标准化处理，使协方差矩阵变为相关系数矩阵，而相关系数矩阵反映的是指标间的线性相关程度，主成分分析的效果与预测指标间相关程度正相关。但是，在实际问题中，若指标个数较多时，第一主成分的贡献率往往难以令人满意，此时，就要选取较多的主成分来满足累计贡献率达到一定水平的要求，这样很容易使主成分分析的降维作用不明显。而且此时原始指标之间多为非线性关系，可以考虑构造原指标的非线性函数对传统主成分进行线性化改进。

非线性主成分分析（non1inear PrinciPa1 comPonent ana1ysis）对原始数据进行对数中心化处理，能提取原始数据的非线性特征。所提取的第一主成分的贡献率较高，能包含数据中的大部分重要信息[15-16]。具体做法为：首先，对原始数据作中心对数化变换

式中：χiJ为第i个样本的第J个指标的观测值，i＝1，2，…，n；l＝1，2，…，p。

然后计算对数中心化的样本协方差矩阵S＝（siJ）p×p

再从协方差矩阵出发进行主成分分析即可。非线性主成分分析的流程图如图1所示。

图1　非线性主成分分析法的计算流程Flg. 1 Flow chart of the nonllnear prlnclpal component analysls

2　径向基函数神经网络

径向基函数（RBF）神经网络是一种三层前向神经网络，包括输入层、隐含层和输出层，其结构模型如图2所示。它能够以任意精度逼近任意连续函数，泛化能力强，收敛及学习速度快[17-18]。

图2　RBF神经网络模型结构Flg. 2 Archltecture of RBF neural network model

RBF网络的基本思想是：用RBF作为隐单元的“基”构成隐含层空间，将输入矢量直接映射到隐空间，隐层节点的作用函数对输入信号在局部产生相应。当RBF的中心点确定后，映射关系也就确定了。而隐含层空间到输出空间是线性映射，即网络的输出是隐单元输出的线性加权和，此处的权即为网络可调参数。因此，网络由输入到输出是非线性映射，而对可调参数而言，网络输出是线性的。这样网络的权就可由线性方程直接解出，从而大大加快学习速度并避免局部极小问题[19-20]。

设RBF神经网络的输入维数为n，学习样本为（X，Y）。其中，输入变量为X＝（X1，X2，…，XN）；输出变量为Xi＝（Xi1，Xi2，…，XiN）T，1≤i≤NJ；训练样本数为N。当神经网络的输入为Xi时，隐含层第J个节点的输出为

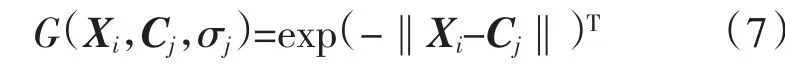
式中：CJ＝（cJ1，cJ2，…，cJn）T为第J个隐含层高斯函数中心；σJ为第J个隐含层高斯函数宽度。

对全体输入学习样本，网络期望输出为

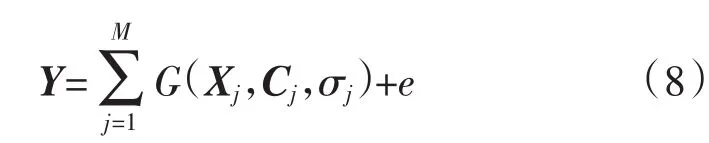
式中：wJ为第个隐含层节点与输出层之间的网络连接权；M为隐含层节点数；e为拟合误差。

本文在选取隐含层高斯函数中心时采用的是正交最小二乘法，同时为使学习训练的总误差达到最小，网络输出权值的训练方法采用的是最小二乘法，即

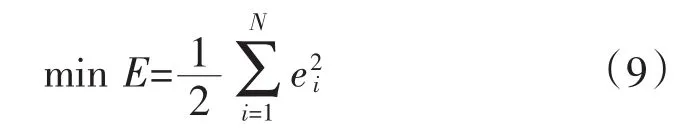
在电力系统负荷预测中，本文以非线性主成分分析得到的主成分作为径向基函数神经网络的输入指标，通过Mat1ab编程得到最终的预测值。

3　实例分析

本文以某省1999—2013年的电力系统负荷（χ9，108kW·h）和固定资产投资总额增长率（χ1，%）、年末从业人口增长率（χ2，%）、人均消费水平增长率（χ3，%）、能源消耗增长率（χ4，%）、农业产值增长率（χ5，%）、工业产值增长率（χ6，%）、建筑业产值增长率（χ7，%），国内生产总值增长率（χ8，%）的数据为原始数据，取1999—2010年的数据作为观测数据，建立电力系统负荷预测模型，以2011—2013年的电力系统负荷数据检验所建模型。

利用SPSS19.0软件对8个相关指标分别作主成分分析和非线性主成分分析，计算得到各指标的特征值、方差贡献率及累计贡献率（见表1和表2）。由表1和表2可知，非线性主成分分析第一个主成分的贡献率达到了95.571%＞85%，即涵盖了原始数据95.571%的信息，而主成分分析第一主成分的贡献率为34.635%，远小于非线性主成分分析的第一主成分贡献率。且在累计贡献率超过98%的前提下，主成分分析需要提取6个主成分，很接近原始指标个数，而非线性主成分分析只需提取2个主成分。由此可知，非线性主成分分析的降维作用和简化问题作用要明显强于主成分分析，所提取主成分保留了原始数据足够的信息。

表1　主成分分析的总方差解释Tab. 1 The explanatlon for total varlance of PCA

表2　非线性主成分分析的总方差解释Tab. 2 The explanatlon for total varlance of nonllnear

根据输出的成分矩阵（见表3和表4），求出主成分系数，具体求法为：各自主成分载荷向量除以各自主成分特征值的算术平方根。根据表5中的成分矩阵，计算得到非线性主成分的表达式为

将提取的2个主成分作为径向基函数神经网络的输入样本，利用Mat1ab编程得到预测结果，同时将使用本文方法得到的结果与使用主成分分析结合径向基神经网络得到的结果和单独使用径向基函数神经网络得到的结果作对比（见表5和表6）。由表5和表6可知，采用非线性主成分分析法处理后的平均相对误差为0.8%，采用主成分分析法处理后的平均相对误差为1.8%，而只采用径向基函数神经网络的平均相对误差为2.0%。预测效果最好的是本文所采用的非线性主成分分析和径向基函数神经网络结合的方法，效果最差的是只采用径向基函数神经网络进行预测的方法，且本文所用方法的输入量最少，为2个，而采用主成分分析法处理和只采用径向基函数神经网络的输入量都较多，分别为6个和8个。可见，非线性主成分分析法更加有效地保留了原始数据的信息，降低了数据的维数和冗余性，简化了网络结构，其预测精度要高于另2种方法。

表3　主成分分析的成分矩阵Tab. 3 Component matrlx of PCA

表4　非线性主成分分析的成分矩阵Tab. 4 Component matrlx of Nonllnear PCA

表5　3种方法的预测结果Tab. 5 The forecastlng results of three methods

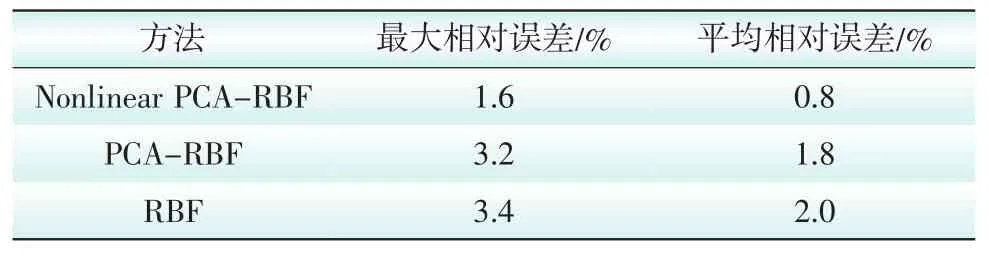
表6　3种方法的预测误差比较Tab. 6 Comparlson of forecastlng errors by three methods

4　结语

由实例可知，相对于主成分分析结合径向基神经网络和单一的径向基函数神经网络法，本文所采用的非线性主成分分析结合径向基函数神经网络法克服了主成分分析法的局限性，兼顾了指标间的非线性关系，在保留原始数据充足信息的前提下，消除了指标的相关性，明显提高了降维效果，减少了电力系统负荷预测的工作量。然后将非线性主成分分析法提取的主成分作为RBF神经网络的输入量进行建模，从而进一步提高了电力系统负荷预测的精度，是一种可行和有效的电力系统负荷预测方法。

参考文献

[1]康重庆，夏清，刘梅.电力系统负荷预测[M].北京：中国电力出版社，2007：10-40.

[2]王玉龙，崔玉，李鹏，等.基于小波分析改进的神经网络模型电力系统负荷预测[J].电网与清洁能源，2015，31（2）：16-20，27. WANG Yu1ong，CUI Yu，LI Peng，et a1. Load forecasting of Power system based on wave1et ana1ysis imProved neura1 network mode1[J]. Power System and C1ean Energy，2015，31（2）：16-20，27（in Chinese）.

[3]彭显刚.基于RBF神经网络的短期负荷预测方法综述[J].电力系统保护与控制，2011，39（17）：144-148. PENG Xiangang. Review on grid short-term 1oad forecasting methods based on RBF neura1 network[J]. Power System Protection and Contro1，2011，39（17）：144-148. （in Chinese）.

[4]李春祥，牛东晓，孟丽敏.基于层次分析法和径向基函数神经网络的中长期负荷预测综合模型[J].电网技术，2009，33（2）：99-104. LI Chunxiang，NIU Dongxiao，MENG Limin. A comPrehensive mode1 for 1ong and medium-term 1oad forecasting based on ana1ytic hierarchy Process and radia1 basis function neura1 network[J]. Power System Techno1ogy，2009，33（2）：99-104（in Chinese）.

[5]李春林，陈旭红.应用多元统计分析[M].北京：清华大学出版社，2013：53-63.

[6] BURKE D J，O’MALLEY M J. A study of PrinciPa1 comPonent ana1ysis aPP1ied to sPatia11y distributed wind Power[J]. IEEE Trans on Power Systems，2011，26（4）：2084-2091.

[7]王志征，余岳峰，姚国平.基于主成分分析法和自适应神经模糊推理系统的电力负荷预测[J].电力自动化设备，2003，23（9）：39-41. WANG Zhizheng，YU Yuefeng，YAO GuoPing. Power 1oad forecast based on PrinciPa1 comPonent ana1ysis and adaPtive neuro-fuzzy inference system[J]. E1ectric Power Automation EquiPment，2003，23（9）：39-41（in Chinese）.

[8]赵杰辉，葛少云，刘自发.基于主成分分析的径向基函数神经网络在电力系统负荷预测中的应用[J].电网技术，2004，28（5）：35-37，40. ZHAO Jiehui，GE Shaoyun，LIU Zifa. APP1ication of radia1 basic function network based on PrinciPa1 comPonent ana1ysis in 1oad forecasting[J]. Power System Techno1ogy，2004，28（5）：35-37，40（in Chinese）.

[9]周松林，茆美琴，苏建徽.基于主成分分析与人工神经网络的风电功率预测[J].电网技术，2011，35（9）：128-132. ZHOU Song1in，MAO Meiqin，SU Jianhui. Prediction of wind Power based on PrinciPa1 comPonent ana1ysis and Artificia1 neura1 network[J]. Power System Techno1ogy，2011，35（9）：128-132（in Chinese）.

[10]张明理，杨晓亮，滕云，等.基于主成分分析与前向反馈传播神经网络的风电场输出功率预测[J].电网技术，2011，35（3）：183-187. ZHANG Ming1i，YANG Xiao1iang，TENG Yun，et a1. Forecasting of wind farm generation outPut based on PrinciPa1 comPonent ana1ysis and back ProPagation neura1 network[J]. Power System Techno1ogy，2011，35（3）：183-187（in Chinese）.

[11]周永正，袁晓辉，周勇.基于非线性主成分神经网络水泥强度预测研究[J].数学的实践与认识，2013，43（3）：83-91. ZHOU Yongzheng，YUAN Xiaohui，Zhou Yong. The Prediction research about the strength of cement based onthe non1inear PrinciPa1 comPonent neura1 network[J]. Mathematics in Practice and Theory，2013，43（3）：83-91（in Chinese）.

[12]熊志斌.基于非线性主成分分析的信用评估模型研究[J].数量经济技术经济研究，2013（10）：138-150. XIONG Zhibin. Research on credit eva1uation mode1 based on non1inear PrinciPa1 comPonent ana1ysis[J]. The Journa1 of Quantitative & Technica1 Economics，2013（10）：138-150（in Chinese）.

[13]聂宏展，聂耸，乔怡，等.基于主成分分析法的输电网规划方案综合决策[J].电网技术，2010，34（6）：134-138. NIE Hongzhan，NIE Song，QIAO Yi，et a1. ComPrehensive decision-making of a1ternative transmission network P1anning based on PrinciP1e comPonent ana1ysis[J]. Power System Techno1ogy，2010，34（6）：134-138（in Chinese）.

[14]高新华，严正.基于主成分聚类分析的智能电网建设综合评价[J].电网技术，2013，37（8）：2238-2243. GAO Xinhua，YAN Zheng. ComPrehensive assessment of smart grid construction based on PrinciPa1 comPonent ana1ysis and c1uster ana1ysis[J]. Power System Techno1ogy，2013，37（8）：2238-2243（in Chinese）.

[15]陈伯松，叶雪梅，安利.基于非线性主成分分析的最小包围盒计算方法[J].计算机集成制造系统，2010，16 （11）：2375-2378. CHEN Baisong，YE Xuemei，AN Li. Minimum bounding box ca1cu1ation based on non1inear PrinciPa1 comPonent ana1ysis[J]. ComPuter Integrated Manufacturing Systems，2010，16（11）：2375-2378（in Chinese）.

[16]卢艳超，张彩庆.用非线性化的方法对主成分分析法的改进[J].统计与决策，2005（9）：127-128. LU Caichao，ZHANG Caiqing. ImProvement of PrinciPa1 comPonent ana1ysis method by using non1inear method[J]. Statistics and Decision，2005（9）：127-128（in Chinese）. [17]回立川，于淼，梁芷睿.应用近邻传播算法改进RBF的短期负荷预测[J].电力系统及其自动化学报，2015，27（1）：69-73. HUI Lichuan，YU Miao，LIANG Zhirui. Research on e1ectric 1oad short-term forecasting via radia1 basis function neura1 network designed by affinity ProPagation[J]. Proceedings of the CSU-EPSA，2015，27（1）：69-73.

[18]徐建源，张彬，林莘，等.能谱熵向量法及粒子群优化的RBF神经网络在高压断路器机械故障诊断中的应用[J].高电压技术，2012，38（6）：1299-1306. XU Jianyuan，ZHANG Bin，LIN Xin，et a1. APP1ication of energy sPectrum entroPy vector method and RBF neura1 networks oPtimized by the Partic1e swarm in high-vo1tage circuit breaker mechanica1 fau1t diagnosis[J]. High Vo1tage Engineering，2012，38（6）：1299-1306（in Chinese）.

[19]李如琦，褚金胜，谢林峰，等. IAFSA-RBF神经网络在短期负荷预测中的应用[J].电力系统及其自动化学报，2011，23（2）：142-146. LI Ruqi，CHU Jinsheng，XIE Linfeng，et a1. APP1ication of IAFSA-RBF neura1 network to short-term 1oad forecasting [J]. Proceedings of the CSU-EPSA，2011，23（2）：142-146（in Chinese）.

[20]何耀耀，许启发，杨善林，等.基于RBF神经网络分位数回归的电力负荷概率密度预测方法[J].中国电机工程学报，2013，33（1）：93-98. HE Yaoyao，XU Qifa，YANG Shan1in，et a1. A Power 1oad Probabi1ity density forecasting method based on RBF neura1 network quanti1e regression[J]. Proceedings of the CSEE，2013，33（1）：93-98（in Chinese）.

刘晓菲（1989—），男，硕士研究生，研究方向为电力系统控制与优化；

商立群（1968—），男，博士，教授，研究方向为电力系统分析与控制、电磁暂态仿真等。

（编辑冯露）

Project SuPPorted by Science and Techno1ogy Research SuPPorting P1an of Shaanxi Provincia1 Education DePartment（No. 12JK0568）；Natura1 Science Basic Research P1an of Shaanxi Province （No.2014JM2-5077）.

Nonllnear Prlnclpal Component Analysls and RBF Neural Network for Power System Load Forecastlng

LIU Xiaofei，SHANG Liqun
（Schoo1 of E1ectrica1 and Contro1 Engineering，Xi’an University of Science and Techno1ogy，Xi’an 710054，Shaanxi，China）

ABSTRACT：Load forecasting is essentia1 to the oPeration and P1anning of the Power system. To imProve the 1oad forecasting accuracy and to address the Prob1em that the PrinciPa1 com-Ponent ana1ysis method has no obvious effects in reducing the dimension and it takes no consideration the non1inear re1ationshiP between the indexes in the mu1ti-index Prediction system，this PaPer uses the non1inear PrinciPa1 comPonent ana1ysis to imProve the inPut of RBF neura1 network. This method overcomes the constraints of the corre1ation between the data，and reduces the dimension of forecasting indexes，and takes into consideration of the non1inear re1ationshiP between the indexes，and retains sufficient information of the origina1 data，and obtains the PrinciPa1 comPonents of the 1oad forecasting，and remarkab1y reduces the inPut of the radia1 basis function network and imProves the accuracy of Power system 1oad forecasting. The effectiveness of the ProPosed method is va1idated by resu1ts of the case ana1ysis.

作者简介：

收稿日期：2015-11-12。

基金项目：陕西省教育厅科研计划项目资助（12JK0568）；陕西省自然科学基础研究计划资助项目（2014JM2-5077）。

文章编号：1674-3814（2016）01-0047-06

中图分类号：TM715

文献标志码：A