红外透镜偏心差的测量计算
马厉克,陈 静
红外透镜偏心差的测量计算
马厉克1,陈 静2
(1.总装备部武汉军代局驻常德地区军代室,湖南 常德 415007;2.湖南华南光电(集团)有限责任公司,湖南 常德 415007)
偏心差是红外透镜设计、制造的重要参数,直接测量难度大、成本高。从GB/T 7242中相关定义出发,推导了透镜偏心差与两个球面的球心差之间的关系,并与Zemax仿真结果和已有关系式的计算结果进行了对比,验证了其在用可见光下反射成像方式中心偏差测量仪测量计算红外透镜偏心差的有效性。
红外透镜;偏心差;球心差;中心偏差;Zemax
0 引言
在光学系统的设计、制造过程中,中心偏差将带来球差及同类象差[1]、非对称性像差(轴上像点有中心像差中心垂轴色差、视场中心存在中心像散、轴外像点出现像散和切向畸变等)[2]等,因此在设计、制造中都要想办法降低中心偏差。在此过程中发展了多种中心偏差的检测方法[3],主要分为2类(按光源相干性分为准直成像法和干涉测量法,按光线传播方式将其分为反射式测量和透射式测量)4种(反射成像式、透射成像式、反射干涉式、透射干涉式)。
由于中心偏差包括面倾角、球心差、偏心差几个等效的子概念[4],又由于诸如偏心差之类的概念在使用中的存在定义[4-5]上的差异[6],因此在使用中不时遇到概念混淆的情况,如将用反射成像式测量的红外中心偏差测量仪中中心偏差当作偏心差(实为球心差)与设计图纸上的偏心差相对应,导致得出错误的测量结果。本文主要针对偏心差开展研究。
非制冷红外焦平面器件日渐普及,凝视型红外光学系统在民用、军用领域均得到了空前的发展。为了对红外透镜的中心偏差进行准确测量,首先要明白测量方式和涉及的中心偏差的具体定义,其次要知道其测量方法和计算原理。虽然现在出现了透射成像式红外透镜中心偏差(偏心差)测量仪[7],但由于其设计制造难度大、已有产品价格昂贵,故更多的是采用传统的测量可见光透镜中心偏差测量仪,采用反射成像方式测量红外透镜的中心偏差(球心差)[8]。
一个球面透镜主要是由2个球面围成的,因此其偏心差与这2个面的球心差存在一定的关系[5]。通过对球心差与偏心差的关系推导,得到了在可见光透镜中心偏差测量仪下较为准确地得到红外透镜偏心差的方法,参考Zemax软件在红外光学设计[9-10]、设计与制造相互借鉴[11]中的使用进行了本方法的仿真验证及红外透镜偏心差的检测,取得了较好效果。
1 球心差与偏心差的关系
1.1 采用的定义
严格采用GB/T 7242中关于面倾角、球心差和偏心差的定义[4],具体如下(如图1所示):
面倾角:光学表面定心顶点处的法线与基准轴的夹角。
球心差:被检光学表面球心到基准轴的距离。
偏心差:被检光学零件或组件的几何轴在后节面上交点与后节点的距离(在数值上等于透镜绕几何轴旋转时焦点像跳动圆半径)。
在图1中,沿光线传播方向,1、2分别为透镜的前后球面,1、2分别为1、2的球心,l¢为透镜的后截距,¢为透镜的像方焦点。另前后球面曲率半径分别为1、2,透镜的中心厚为,折射率为。
1.2 推导与分析
在薄透镜的情况下,球心差与偏心差之间存在如下关系[5]:

在厚透镜的情况下,光线与透镜几何面及基准轴之间的关系如图2所示。
1)选取透镜第1面为基准面,第2面有中心偏差,即1=02≠0,则光线如图2所示。
主光线经过第1面后,在第2面处发生偏折,成像于焦平面上。成像点到基准轴(几何轴)的距离为偏心差(),由折射定律可得出:
×=¢
由图1可得出:
=¢-
==2/2
则计算得偏心差()为:

从上述分析可知,使用公式(2)的前提是透镜的第1个面作为基准面(1=0),第2个面有中心偏差。
2)在实际检验测量过程中,是以第2个面作为基准面来测量的,并且该基准面只有在理想情况下其球心偏2=0,但实际上由于仪器工装误差的累积,该基准面球心偏2≠0,其数值很小。

图1 光学参数c, a, c的定义

图2 a1=0、a2≠0时中心光线传播情况
主光线经过透镜第1面后发生偏折,光线对第1面的入射角1=1,折射角1′=1′,根据折射定律可得出:1=1′。于是:
①对第2面,可先求出理想情况下(2=0)的入射角2=m,如图3所示:


由折射定律得出,光线对第2面的折射角m′:
m′=×m
由图可知:

由中心偏定义可知:
1=1/1
则计算得偏心差为:
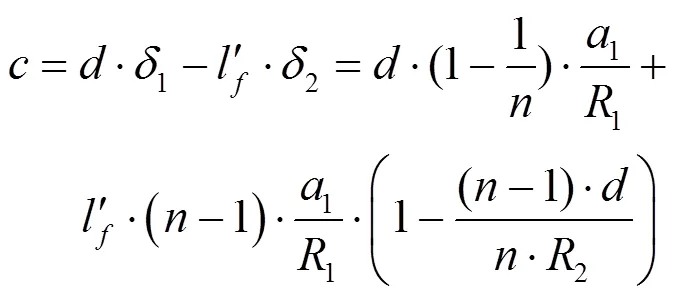



由图可知:
由中心偏定义可知:1=1/1,2=2/2

公式(1)~(4)在实际使用中可以根据情况进行选用,而式(4)是其中最为一般性的公式。

图4 a1≠0、a2≠0时中心光线传播情况
整理式(4)得:

式中:第1项为以第2个球面为参考面的第1个球面的偏心差、第3项为以第1个球面为参考面的第2个球面的偏心差、第2项为透镜厚度的影响。
在=0时,式(5)退化为:

与式(1)相比,式(6)的优点较为明显,在薄透镜的情况下:
1)透镜的偏心差等于2个球面的偏心差的和,物理意义更清晰;
2)不存在奇异的情况(1=2),适用范围更广。
另外,与式(1)的推导一样,式(2)~(6)也是在2个球面偏心点与参考轴共面的情况下推导的,其中的符号选择也以使偏心差取值最大为准,以便能控制其在规定公差范围内。
2 测量计算实例
在中心偏差测量仪器中,有能够以反射成像式同时测得透镜2个球面差的仪器,如OptiCentric MOT Dual。用其对下述系列红外透镜进行球心偏1、2的测量:1=34.61mm、2=37.67mm,中心厚=4mm,折射率为=4,后截距l′=65.42mm,各透镜存在不同的球心偏。然后用测量数据按照4种方式进行偏心差的计算、对比:
方式1:用软件Zemax计算;
方式2:用厚透镜时的式(5)计算;
方式3:用薄透镜时的式(6)计算;
方式4:用薄透镜时的式(1)计算。
具体测量、计算结果如表1所示。
从表1看,以Zemax计算结果为参考,式(1)、(5)、(6)的准确性顺序为式(5)>式(6)>式(1),相对于参考值的最大相对误差分别为2.6%、10.3%、110.7%。从计算结果的对比可以看出,推导的式(5)、(6)具有较好的准确性,可分别应用于薄、厚透镜(尤其是红外透镜)的偏心差的测量计算。
3 结论
为了能用可见光下反射成像方式中心偏差测量仪测量红外透镜的偏心差,基于GB/T 7242中关于偏心差的定义,推导了在厚透镜情况下的偏心差与透镜两个球面的球心差之间的关系,并在厚度为0时退化得到薄透镜下的相应关系。通过与Zemax的仿真结果、已有的薄透镜下的偏心差-球心差公式计算结果进行对比,验证了本文推导公式的有效性,对红外透镜的设计、制造与检验都具有较好的参考意义。

表1 偏心差计算对比表
[1] 樊学武, 陈荣利, 马臻, 等. 偏心和倾斜光学系统初级像差理论的研究[J]. 光子学报, 2004, 33(4): 494-496.
FAN Xue-wu, CHEN Rong-li, MA Zhen, et al. Astudy on the primary aberration theory of decentered and tilted optical system[J]., 2004, 33(4): 494-496.
[2] 林大健. 光学系统偏心公差计算方法[J]. 光学学报, 1982, 2(1): 18-27.
LIN Da-jian. A method of deciding tolerances of decentered optical systems [J]., 1982, 2(1): 18-27.
[3] 方超, 于长淞. 镜片中心偏差测量方法发展现状[J]. 光机电信息, 2011, 28(8): 17-21.
FANG Chao, YU Chang-song. Development of centering errors measurement [J]., 2011, 28(8): 17-21.
[4] 中国机械工业联合会. GB/T 7242-2010,透镜中心偏差[S]. 中华人民共和国质量检验检疫总局, 中国国家标准化管理委员会. 2010.
China Machinery Industry Federation. GB/T 7242-2010, Centering errors of lenses[S]. General Administration of Quality Supervision, Inspection and Quarantine of the People’s Republic of China, Standardization Administration of the People’s Republic of China, 2010.
[5] 舒朝濂, 田爱玲, 杭凌侠, 等. 现代光学制造技术[M]. 北京: 国防工业出版社, 2010: 151-152.
SHU Chao-lian, TIAN Ai-ling, HANG Ling-xia, et al.[M]. Beijing: National Defenses Industry Press, 2010: 151-152.
[6] 杨力. 透镜偏心差的定义及单透镜偏心差的检测[J]. 西安工业大学学报, 1982(2): 39-48.
YANG Li. Definition of decentering error and test of the error of a single lens [J]., 1982(2): 39-48.
[7] TIAN Hebin. Centering Measurement of Infrared Lenses with OptiCentric and OptiCentric InfraRed[R/OL]. Germany: Tri-Optics GmbH, http//www.trioptics.com, 2013.
[8] Patrik Langehanenberg.OptiCentric Motorized操作手册[R/OL]. 北京: 全欧光学检测仪器有限公司, 2005, http//www.trioptics-china.com.
Patrik Langehanenberg. OptiCentric Motorized Operation Manual[R/OL]. Beijing: Tri-Optics China, 2005.
[9] 杜玉楠, 牟达, 刘莹莹, 等. 20×长波红外变焦光学系统设计[J]. 红外技术, 2013, 35(10): 607-611.
DU Yu-nan, MU Da, LIU Ying-ying, et al. Design of 20×long wavelength infrared zoom optical system[J]., 2013, 35(10): 607-611.
[10] 李维善, 陈琛, 于国辉, 等. 单机数字立体双通道放映镜头的光学设计[J]. 中国光学,2013, 6(4): 563-569.
LI Wei-shan, CHEN Chen, YU Guo-hui, et al. Optical design of single digital stereo dual-channel projection lens[J]., 2013, 6(4): 563-569.
[11] 张华卫,张金旺,刘秀军,等. 大相对孔径制冷型红外相机镜头的光学设计[J]. 红外技术, 2015,37(2):124-129.
ZHANG Hua-wei, ZHANG Jin-wang, LIU Xiu-jun, et al. Design of low f-number lens for cooled infrared camera[J]., 2015,37(2):124-129.
Measurement and Calculation of the Prejudicial Aberration of Infrared Lenses
MA Like1,CHEN Jing2
(1.,415007,;2.(),415007,)
Prejudicial aberration is an important parameter in design and manufacture of infrared lenses, direct measurement of which is hard and costs high. From the definitions in GB/T 7242, the relationship between prejudicial aberration and spherical center aberrations of a lens is deduced.Compared with the simulation result by Zemax and calculation result of an existed formula, the validity of the relationship is verified.
infrared lens,prejudicial aberration,spherical center aberration,centering error of lenses,Zemax
TN211,TN216
A
1001-8891(2016)03-0250-05
2015-09-06;
2015-12-29.
马厉克(1975-),男,江苏溧水人,博士,高级工程师,主要从事光电设备设计、制造及检测领域的研究。E-mail:malike@sina.com。

