增强型地热系统中液-岩化学作用数值模拟研究*
陈继良,黄文博,曹文炅,蒋方明
(中国科学院可再生能源重点实验室,中国科学院广州能源研究所先进能源系统实验室,广州510640)
增强型地热系统中液-岩化学作用数值模拟研究*
陈继良,黄文博,曹文炅,蒋方明†
(中国科学院可再生能源重点实验室,中国科学院广州能源研究所先进能源系统实验室,广州510640)
摘 要:增强型地热系统(Enhanced Geothermal System, EGS)利用深层岩石中连通的裂隙网络进行流体工质循环,从而实现地热能的持续开采。EGS运行时循环流体工质会与深层岩石产生化学反应,引起岩石中矿物的溶解/沉积,使热储中的裂隙网络形貌产生动态变化,对地下流动与传热过程造成影响。本文分析了EGS中液–岩化学作用特点,详细阐述了在多孔介质热流动模型中耦合入液–岩化学反应的方法,基于已开发成功的EGS传热传质数值模型初步建立了传热–流动–化学(Thermal-Hydraulic-Chemical, THC)多场耦合数值模型,并使用该模型对五井布局EGS的长期运行过程进行了模拟分析,模拟时仅考虑方解石在水流体中溶解和沉积。模拟结果显示,循环流体的注入温度以及注入流体中的矿物离子浓度的设定十分重要。如果二者没有达到较为合适的“平衡”,就会导致注入井附近渗透率和孔隙率的持续变化,对EGS的导流能力造成极大影响。
关键词:增强型地热系统;液-岩化学作用;数值模拟
0 引 言
地下3 ~ 10 km范围内低渗透性结晶质干热岩(Hot Dry Rock, HDR)中储藏着大量的热能,开发利用深层地下热能对缓解当前能源危机、减轻常规化石能源利用所带来的环境污染有重要意义[1-3]。增强型地热系统(Enhanced Geothermal System, EGS)借助人为措施(如水力致裂)在HDR内建立高渗透性的人工热储,通过采热流体工质在地下热储中的循环流动来汲取HDR中的热能,获得高温流体用于地面发电[1,4]。EGS整个采热过程清洁无污染,热量来自地下,系统输出功率不受天气和昼夜交替的影响,连续性和稳定性佳[5]。增强型地热系统被认为是地热能未来的发展方向[1,6-7]。
EGS区别于常规水热型地热系统的重要特点是其开采的热能位于地层深处的结晶质干热岩内,岩石渗透率、孔隙率极低。研发裂隙激发技术,建立体积和展布面积足够大、渗透性和连通性足够好、裂隙比表面积大的有效人工热储是建立采热效率高、可持续性好的EGS电站的关键[1,4,8]。借助于先进的数值模型研究EGS地下岩体中的多场耦合过程,可揭示相关的基础机制,评估采热性能,为EGS合理设计和优化服务。数值模拟方法在EGS研发工作中的应用越来越广泛[9-10]。
EGS利用深层岩石中连通的裂隙网络进行流体工质循环,从而实现地热能的持续开采。这种开采过程将会改变热储中温度和化学平衡,循环流体工质将会与深层岩石产生化学反应,引起岩石中矿物的溶解/沉积,使热储中的裂隙网络形貌产生动态变化,对地下流动与传热过程造成影响。
针对EGS地下流动与传热过程特点,我们开发了EGS三维传热传质模型[11-12]。该模型将EGS地下部分处理成单区多子域,视不同子域为具有不同渗流特性的等效多孔介质;考虑到注入的采热工质和地下热储岩体之间往往存在较大温差,引入岩石–流体间非热平衡概念,使用两个能量方程分别描述流体和岩石的温度场。相比其他的EGS模型(如TOUGH2[13],TOUGHREACT[14]),我们的模型物理概念更清晰、物性参数的设定更方便,而且能够模拟实际EGS中的局部对流热交换过程。
为了研究液–岩化学作用对EGS采热过程的影响,本文在以前模型[11-12]基础上耦合了液–岩化学反应过程,初步建立了传热–流动–化学(Thermal-Hydraulic-Chemical, THC)多场耦合数值模型,并使用该模型对五井布局EGS的长期运行过程进行了模拟分析。
1 EGS中的化学反应特点及模拟方法
EGS运行时,注入的流体一般与深层地下的初始地质化学环境间存在较为明显的化学不平衡势。地下岩石成分复杂,不同的岩石中有时会包含同种元素,如白云石和方解石中都包含钙元素。这使得液–岩化学反应时,一种岩石中的化学反应过程会影响其他岩石的溶解或沉积,而其他岩石的溶解或沉积又反过来会影响该岩石中的化学过程。在EGS中,地下流体组分浓度往往较大,在分析液岩相互作用时,流体一般不能被视为理想溶液,必须考虑非理想溶液中离子间的相互影响。
理想溶液中,溶质或溶剂均遵守拉乌尔定律,没有体积变化和热效应。拉乌尔定律指稀溶液中溶剂A的蒸汽压pA,等于同一温度下纯溶剂的饱和蒸气压与溶液中溶剂A的摩尔分数xA的乘积:

所谓稀溶液是指xA接近1的溶液,理论上讲应该是理想溶液。式中p*A指纯溶剂A的饱和蒸气压。但实际溶液往往与理想溶液有明显差别。不同粒子之间的相互作用与相同粒子之间的作用有时差别很大,甚至有些还会发生化学反应,这时体积的变化和热效应变得不可忽略,溶质或溶剂将不再严格遵守拉乌尔定律,需要引入修正因子来考虑异种分子间作用与同种分子间作用的差别:

采用活度概念来表示非理想溶液中的粒子浓度,其表达式为:

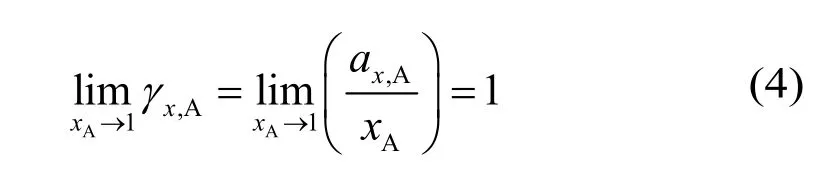
活度在非理想溶液中的含义就相当于理想溶液中的浓度。活度系数用一种最直观、最简洁的方式表达了溶液中多种粒子间的复杂作用,极大地便利了非理想溶液中物理化学变化的研究。当前,EGS模拟中有多个模型用来计算采热工质内离子活度系数。离子活度系数计算方式的不同是当前EGS模拟中不同化学模拟方法的主要区别。EGS中,溶液温度的变化范围也很大,导致液–岩平衡态在时空方向上持续变化,且反应过程与流体流动传热形成强烈的耦合关系。
岩石化学反应速率的求取是地下化学场模拟中的关键问题。在研究液–岩化学反应时,人们基于岩石的微观溶解和微观沉积是一直同时发生的这一基本共识。当溶解速率大于沉积速率时,宏观的表现就是岩石溶解,反过来则是沉积。在这样一种认知下,液–岩化学反应速率其实是溶解速率与沉积速率之差。当前广泛使用的模拟地下液岩作用过程的数值模型中,普遍认同并使用这一计算思路(TOUGHREACT[14],FRAChem[15],SHEMAT[16],EQ3NR[17])。
理解液岩微观作用过程对实际结果的分析有重要启示作用。岩石的溶解和沉积实际上是同一个问题的两个方面,其微观作用机制非常相似。岩石溶解的微观机制可描述如下:水–岩反应时,接触界面上会形成淋溶层,矿物质从未反应的岩石主体部分以扩散的方式通过淋溶层转移至溶液中。溶解初期,淋溶层逐渐变厚。随着溶解过程的进行,淋溶层逐渐加厚,溶液中矿物浓度随之升高,淋溶层两侧矿物浓度差不断降低,矿物离子在淋溶层中的定向扩散速率渐渐变小,直至与外界溶液中矿物离子“反向扩散”进入岩石基体的速率相同,达到化学平衡[18]。矿物的沉积过程与之相似,只是初始的矿物离子宏观转移方向相反。在这种机制下,化学反应的控制步骤就划分为两个重要环节:矿物在淋溶层中的扩散和反应界面上矿物离子的转移。当界面反应速率不大时,扩散到反应界面上的矿物不能及时通过溶入流体而转移时,液–岩作用过程就极大地受控于界面处的化学反应速率,具有这种特点的化学反应就被称为表面控制反应。反过来,当界面处化学反应速率相对较大,而矿物的扩散较慢时,矿物的扩散过程占据了反应的绝大多数时间,这种类型的反应则被称为缩核反应[18-19]。
在EGS中,流体与岩石间的表面化学反应速率往往极低,因此通常遇到的反应类型都是表面控制的化学反应。这样,矿物离子在流体中的物理化学特性对整个反应过程起到了主要作用。研究发现,溶解速率常数主要取决于pH值及温度,而与其它溶解成分的浓度基本无关。虽然仍有许多因素需要考虑,但液–岩化学反应的这个特点使得化学反应速率这一关键参数的确定思路变得明了。
同FRAChem、TOUGHREACT、SHEMA等当前广泛应用的地质化学模拟软件一样,本文也使用Lasaga提出的方程来确定矿物的化学反应速率:

式中,Q为化学反应商(reaction quotient),Keq为化学平衡常数(chemical equilibrium constant),ki是矿物i的反应速率常数(kinetic rate constant),参数θ 和η的值需由实验确定。根据水–岩作用过程特点,常见的矿物溶解反应速率常数可由下式计算[20]:

式中:k25为常温(25℃,即298.15K)时相应矿物的反应速率常数;Ea为活化能(activation energy);R为气体常数(gas constant);T为绝对温度;上标nu、H和OH分别为中性、酸性和碱性作用机制;a为相应离子的活度;n为调节参数(常数)。
当前,常温下矿物的反应速率常数k25及相应矿物的活化能Ea已可准确测定,相关数据库已比较完善[20]。因此,化学反应速率Rθ的确定关键在于准确计算化学平衡常数Keq和化学反应商Q的值。一般认为,化学平衡常数仅与温度有关,目前针对地质岩石的化学反应平衡常数的计算已做了大量研究,基本获得较为统一的计算方法(如SUPCRT92、Thermoddem、EQ3NR、WATEQ4F、SOLMINEQ、PHRQPITZ、PHREEQC等计算软件)。本文开发的模型中,使用的是Thermoddem数据库提供的化学平衡常数数据[21]。
结合对现有的地质化学模型的研究,我们认为化学反应商的计算是目前EGS地下矿物溶解/沉积模拟的难点。由于EGS中采热流体中离子浓度较大,将其视为理想溶液会带来极大误差,因此化学反应商又涉及到各离子活度系数。浓溶液中的离子活度系数计算向来是一个不确定性很大的科学问题,目前虽然已有多个计算模型(如Debye-Huckel模型,Davies模型,Pitzer模型等),但计算精度仍不能保证。ANDRÉ等[22]对比了不同活度系数计算方式对模拟结果的影响,得出不同的活度系数计算模型会导致不同的模拟结果。目前,关于浓溶液中离子活度的计算仍没有统一的准确公式。
溶液密度会随离子浓度而变化,但由浓度改变导致的密度变化量相对于温度和压强带来的变化是很小的。本文关于液岩反应的计算中未考虑密度的变化。
模型的假设见文献[12],另外还假设仅有固体岩石和液体工质间的化学作用。所需求解的控制方程如下。
连续方程:
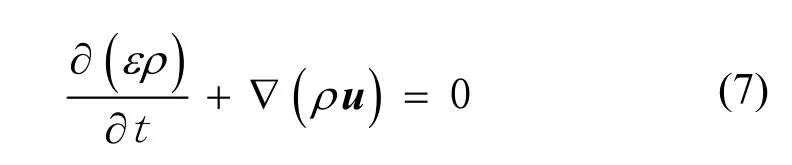
动量方程:
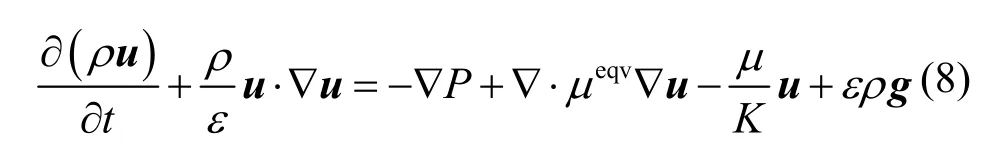
流体的能量方程:
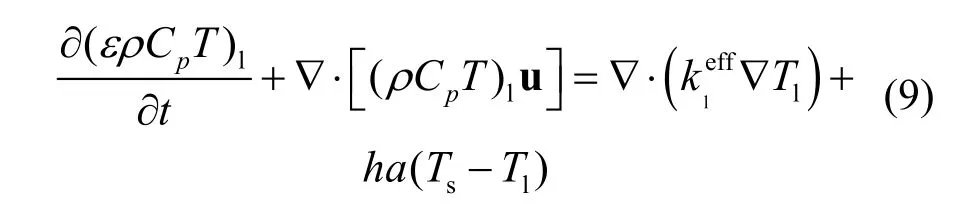
岩石的能量方程:

离子浓度方程:
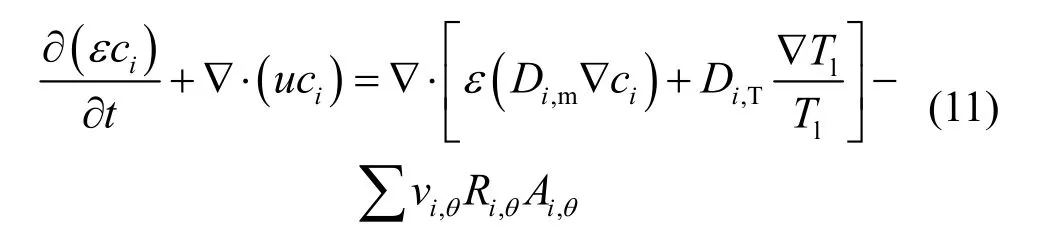
岩石体积分数方程:
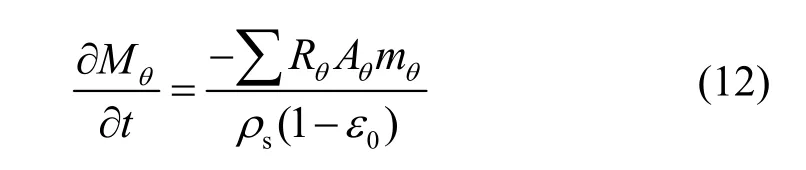
热储孔隙率的变化规律:
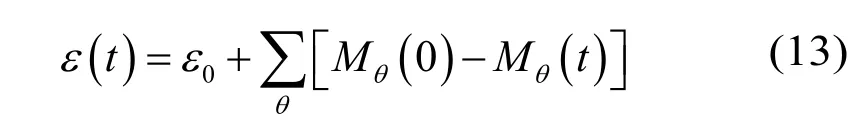
式中:ε、ρ、u、P、μ、K、Cp和g分别表示热储孔隙率、密度、流体表观速度、压强、流体动力粘性系数、热储渗透率、比热容和重力加速度;下标s 和l分别代表岩石和流体;上标eff表示有效物性;ci表示离子i的物质的量浓度;Di,m为离子i的扩散系数;Di,T表示离子i的索雷效应(Soret effect)系数;t为时间;Tl表示流体温度;νi,θ为固体矿物θ的化学反应中离子i的反应系数;Ri,θ为固体矿物θ的溶解速率(正值表示溶解,负值表示沉积);Aθ为固体矿物θ的比反应面积;Mθ为固体矿物θ的体积分数;mθ表示矿物θ的摩尔质量;ρs表示岩石密度;ε0为热储的初始孔隙率。ha为对流换热系数和裂隙比表面积的乘积,表示岩石–流体对流换热基础条件。
数值求解采用通用计算流体软件FLUENT6®,岩石温度、流体温度及各离子浓度方程都定义为Fluent的用户自定义标量(User Define Scalar,UDS)。每个时间步,均首先更新热储内的局部孔隙率和渗透率,然后连续方程、N-S方程及所有UDS方程耦合求解至满足各自的收敛条件,继而开始下一时间步的计算求解。详细求解方法参阅文献[12]。
在等效多孔介质模型中,渗透率和孔隙率是描述热储宏观导流特性的核心参数。方程(13)的物理意义是热储孔隙率的增加量等于热储内岩石体积分数的减少量。在不考虑岩石热应变的情况下,这种计算方式是比较合理的,目前应用十分广泛[14-15,23]。但渗透率是一个更为复杂的参数,它无法直接从裂隙网络的形态进行直接判断。大量研究表明,孔隙率相同的多孔介质,渗透率可能差别很大[24-25]。EGS热储属于裂隙多孔介质,孔隙率极低且内部裂隙网络分布极为复杂,当前任何孔隙率–渗透率关系式在应用到EGS的数值模拟时精度都难以保证。研究不同地质条件下孔隙率和渗透率的关系对于提高EGS中的化学反应及力学应变的模拟精度有重要意义。本文探讨的是THC模拟的初步结果,暂使用的孔隙率–渗透率关系方程如下。
维尔玛–普利斯(Verma-Pruess)关系式:

式中,k和ε分别为热储实时有效渗透率和孔隙率,k0和ε0则为热储初始渗透率和初始孔隙率。εc为临界孔隙率,其物理意义是当孔隙率降低到该值时,热储的有效渗透率降低为零。n和εc的取值与多孔介质的材料性质有关。
2 算例设置
实际的干热岩热储中包含多种类型的岩石,成分复杂且空间分布难以确定。本文所述计算主要用于校验模型可行性,暂仅考虑液体与方解石的相互作用。方解石水解反应方程式:
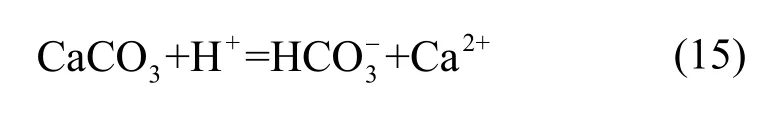
所用几何模型采用五井布局EGS,几何设置如图1所示。

图1 模型几何尺寸Fig. 1 Geometry and dimensions of the quintuplet EGS
采热工质和岩石的热物性参数如表1列示。设定热储初始孔隙率和渗透率皆均匀分布,其值分别为0.01和10–14m2,孔隙率–渗透率关系式中取临界渗透率εc为0.008,修正指数n为1。测试算例暂使用常活度系数模型(γH= 0.1,γHCO3= 0.1,γCa= 0.01)。注入流体温度为343.15 K,热储中初始矿物浓度及注入流体中矿物离子浓度如表2所示。初始的方解石和白云石体积分数分别设定为4.3%。岩石水解反应速率常数k25、反应活化能等参数参考文献[20]。方解石化学平衡常数采用下式[21]:
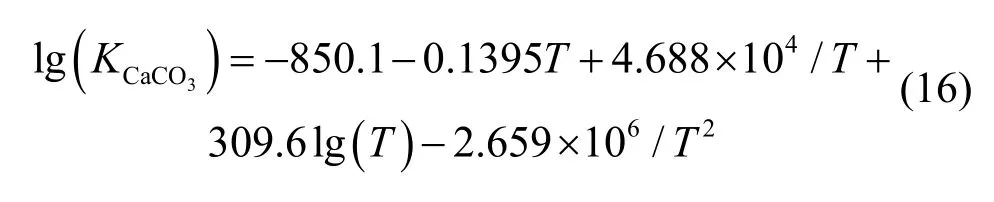

表1 物理性质Table 1 Physical properties

表2 热储中天然流体矿物离子浓度和注入采热工质的矿物浓度Table 2 Initial/injected water chemical compositions
3 模拟结果与分析
图2、图3显示的是定循环流量下(50 kg/s)热储内pH值的空间分布随时间的改变及液岩化学反应对生产流体温度和地热开采率的影响。
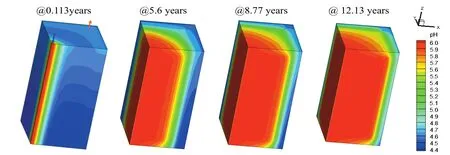
图2 热储内裂隙流体pH值分布随时间的变化Fig. 2 Evolution of pH in the reservoir
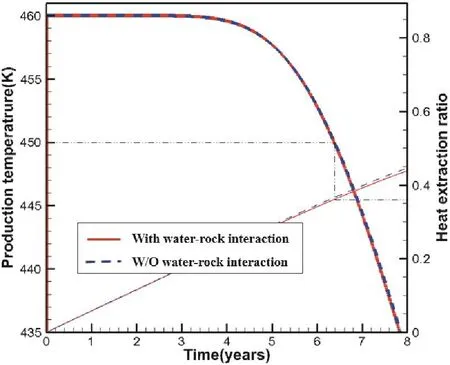
图3 液岩反应对生产流体温度与采热率的影响Fig. 3 The influence of water-rock interaction on production temperature and heat extraction ratio
根据方解石的水解反应式可知,pH值的增大意味着矿物溶解,反之则意味着沉积。热储内裂隙流体的初始pH值是5.03,可以看到在该设置下热储内绝大多数区域表现为矿物的持续溶解。值得注意的是,该设置下得出的结论是液岩化学反应几乎不影响运行寿命及地热开采率。我们对运行过程中的速度场、温度场进行了仔细对比,亦发现其与忽略液岩相互作用的算例几乎没有差别。但这并不意味着可忽略液岩化学反应对采热过程的影响。图4、图5显示了定注入压力下(10 MPa)热储内pH值的空间分布随时间的改变及液岩化学反应对生产流体温度和地热开采率的影响。
可以看到,热储内裂隙流体的pH值随时间的变化趋势与定质量流量的算例非常相似,但这时EGS的运行寿命和地热开采率却有了较为明显的改变。之后的计算中,无论是使用Debye-Huckel离子活度模型还是Davies模型,所得结论均极为相似。虽然这些结果基于大量假设且忽略了流体热物性参数的变化,但仍可结合前文所做的流场–温度场研究,通过分析热储内化学反应特点,得出一些有用的结论。
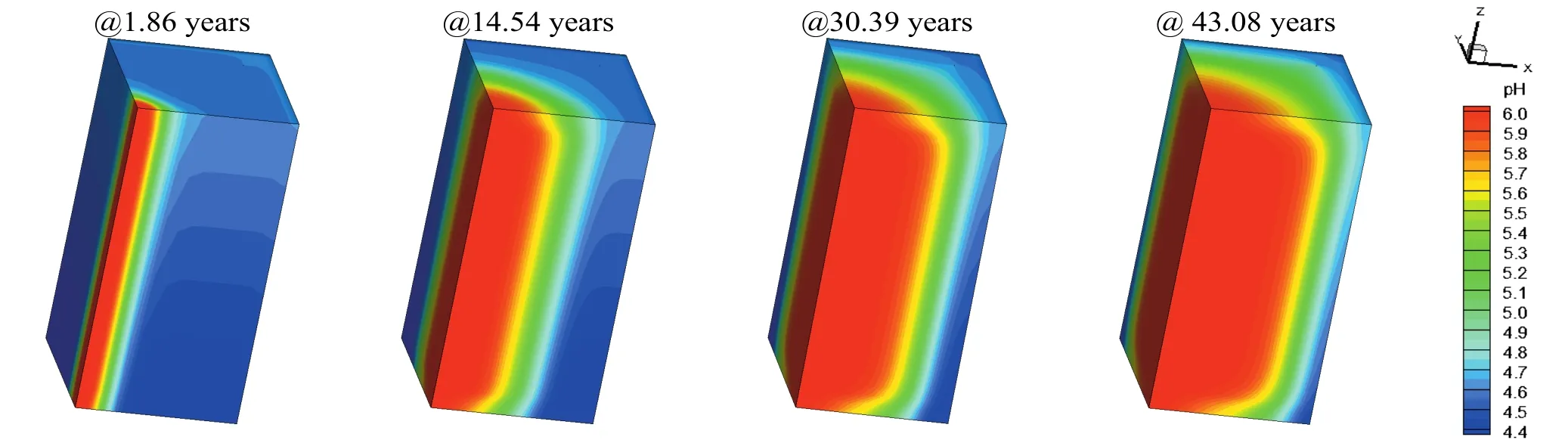
图4 热储内裂隙流体pH值分布随时间的变化(注入压力10 Mpa)Fig. 4 Evolution of pH in the reservoir (pressure inlet 10 Mpa)

图5 液岩反应对生产流体温度与采热率的影响(注入压力10 MPa)Fig. 5 The influence of water-rock interaction on production temperature and heat extraction ratio
EGS的运行中,流体阻力主要集中于注入井和生产井附近。井附近裂隙网络结构的改变将在很大程度上影响热储的导流能力。当裂隙激发完毕,EGS开始运行后,注入井附近的岩石温度迅速降低,局部温度场(数米至数十米范围内)在较短时间内(数天至数月)就可达到稳定。这样,注入井附近区域在运行早期就处于“准定温”状态,当注入流体的矿物组份恒定时,各岩石水解反应的化学反应商、化学平衡常数等参数将不再变化。由此计算所得的化学反应速率自然也为恒定值。因此可以得到这样一个结论:虽然EGS运行寿命很长,地下液岩相互作用复杂多变,但注入井附近岩石的溶解/沉积速率在运行初期就已趋于稳定,EGS运行过程中注入井附近的岩石将持续地以接近恒定的速率溶解或沉积,受此影响,注入井附近的裂隙网络结构也会持续发生改变,进而极大地影响热储的整体导流能力。展示的图中,注入井附近岩石表现为溶解,局部孔隙率和渗透率将持续增大,热储导流能力不断提高,在相同的注入压力下,采热工质的循环流量就会逐渐增大。
以上分析说明,注入流体的温度和注入流体中的矿物离子初始浓度十分重要,并且两者的设定不应该是独立的。注入温度决定了地下热能的开采极限,其确定往往要考虑如地面热电转换设备的性能等地下THMC过程难以改变的因素,客观性较强。在注入温度难以改变的情况下,控制液岩化学反应对地下热储裂隙结构的拓展或堵塞效应时,就需要根据温度值的大小调整注入流体的矿物离子浓度。如果二者没有达到较为合适的“平衡”,就会导致注入井附近渗透率和孔隙率的持续变化,对EGS的导流能力(直接影响生产效率或净输出功)造成极大影响。
4 总 结
文章分析了EGS中液–岩化学作用特点,详细阐述了THC全耦合数值模拟的实现方法,并使用该模型对五井布局EGS的长期运行过程进行了模拟。
所设置算例的模拟结果显示,热储中岩石−流体间的化学作用表现为溶解作用。受此影响,热储中部分裂隙区域局部孔隙率和渗透率不断增大,导致热储裂隙的导流能力发生显著改变。当EGS在恒定循环压力下运行时,该作用会使循环流量逐渐增大,并对系统的热开采情况造成明显的影响。进一步的分析表明,循环流体的注入温度以及注入流体中的矿物离子浓度的设定十分重要。如果二者没有达到较为合适的“平衡”,就会导致注入井附近渗透率和孔隙率的持续变化,对EGS的导流能力(直接影响生产效率或净输出功)造成极大影响。
后续研究工作中,我们将进一步完善模型,考虑非均质热储、多相流效应等,研究注入流体参数对岩石–流体间化学作用的影响。
参考文献:
[1] TESTER J W, ANDERSON B J, BATCHELOR A S, et al. The future of geothermal energy: impact of Enhanced Geothermal Systems (EGS) on the United States in the 21st century[M]. Cambridge: Massachusetts Institute of Technology, 2006: 1-358.
[2] 汪集旸, 胡圣标, 庞忠和, 等. 中国大陆干热岩地热资源潜力评估[J]. 科技导报, 2012, 30(32): 25-31. DOI: 10.3981/j.issn.1000-7857.2012.32.003.
[3] TENZER H. Development of hot dry rock technology[J]. Bulletin geo-heat center, 2001, 32(4): 14-22.
[4] U.S. Department of Energy. An evaluation of enhanced geothermal systems technology[R]. Washington, DC: EERE, 2008.
[5] LACIRIGNOLA M, BLANC I. Environmental analysis of practical design options for enhanced geothermal systems (EGS) through life-cycle assessment[J]. Renewable energy, 2013, 50: 901-914. DOI: 10.1016/ j.renene.2012.08.005.
[6] BERTANI R. Geothermal power generation in the world 2005-2010 update report[J]. Geothermics, 2012, 41: 1-29. DOI: 10.1016/j.geothermics.2011.10.001.
[7] 庞忠和, 胡圣标, 汪集暘. 中国地热能发展路线图[J].科技导报, 2012, 30(32): 18-24. DOI: 10.3981/j.issn. 1000-7857.2012.32.002.
[8] MCCLURE M W. Fracture stimulation in enhanced geothermal systems[D]. San Francisco, California: Stanford University, 2009.
[9] O'SULLIVAN M J, PRUESS K, LIPPMANN M J. State of the art of geothermal reservoir simulation[J]. Geothermics, 2001, 30(4): 395-429. DOI: 10.1016/ S0375-6505(01)00005-0.
[10] KOHL T, EVANSI K F, HOPKIRK R J, et al. Coupled hydraulic, thermal and mechanical considerations for the simulation of hot dry rock reservoirs[J]. Geothermics, 1995, 24(3): 345-359. DOI: 10.1016/0375-6505(95) 00013-G.
[11] JIANG F M, LUO L, CHEN J L. A novel three-dimensional transient model for subsurface heat exchange in enhanced geothermal systems[J]. International communications in heat and mass transfer, 2013, 41: 57-62. DOI: 10.1016/j.icheatmasstransfer. 2012.11.003.
[12] JIANG F M, CHEN J L, HUANG W B, et al. A three-dimensional transient model for EGS subsurface thermo-hydraulic process[J]. Energy, 2014, 72: 300-310. DOI: 10.1016/j.energy.2014.05.038.
[13] PRUESS K. The tough codes-a family of simulation tools for multiphase flow and transport processes in permeable media[J]. Vadose zone journal, 2004, 3(3): 738-746. DOI: 10.2113/3.3.738.
[14] XU T F, SONNENTHAL E, SPYCHER N, et al. TOUGHREACT-A simulation program for non-isothermal multiphase reactive geochemical transport in variably saturated geologic media: applications to geothermal injectivity and CO2geological sequestration[J]. Computers & geosciences, 2006, 32(2): 145-165. DOI: 10.1016/j.cageo.2005.06.014.
[15] BÄCHLER D. Coupled thermal-hydraulic-chemical modelling at the Soultz-sous-Forêts HDR Reservoir (France)[D]. Zurich: Swiss Federal Institute of Technology Zurich, 2003.
[16] CLAUSER C. Numerical simulation of reactive flow in hot aquifers: SHEMAT and processing SHEMAT[M]. Berlin Heidelberg: Springer, 2003.
[17] WOLERY T J. EQ3NR, a Computer program for geochemical aqueous speciation-solubility calculations: theoretical manual, user's guide and related documentation (version 7.0)[M]. California: LawrenceLivermore Laboratory, University of California, 1992.
[18] LASAGA A C. Chemical kinetics of water-rock interactions[J]. Journal of geophysical research: solid earth (1978-2012), 1984, 89(B6): 4009-4025. DOI: 10.1029/JB089iB06p04009.
[19] BRANTLEY S L, KUBICKI J D, WHITE A F. Kinetics of water-rock interaction[M]. New York: Springer, 2008.
[20] PALANDRI J L, KHARAKA Y K. A compilation of rate parameters of water-mineral interaction kinetics for application to geochemical modeling[R]. Menlo Park, California: National Energy Technology Laboratory-United States Department of Energy, 2004.
[21] BLANC P, LASSIN A, PIANTONE P, et al. Thermoddem: a geochemical database focused on low temperature water/rock interactions and waste materials[J]. Applied geochemistry, 2012, 27(10): 2107-2116. DOI: 10.1016/j.apgeochem.2012.06.002.
[22] ANDRE L, SPYCHER N, XU T, et al. Comparing FRACHEM and TOUGHREACT for reactive transport modeling of brine-rock interactions in Enhanced Geothermal Systems (EGS)[C]//31st workshop on geothermal reservoir engineering. Stanford, California: Stanford University, 2006.
[23] MACQUARRIE K T B, MAYER K U. Reactive transport modeling in fractured rock: a state-of-thescience review[J]. Earth-science reviews, 2005, 72(3/4): 189-227. DOI: 10.1016/j.earscirev.2005.07.003.
[24] XU P, YU B M. Developing a new form of permeability and Kozeny-Carman constant for homogeneous porous media by means of fractal geometry[J]. Advances in Water Resources, 2008, 31(1): 74-81. DOI: 10.1016/j. advwatres.2007.06.003.
[25] EHRENBERG S N, NADEAU P H. Sandstone vs. carbonate petroleum reservoirs: a global perspective on porosity-depth and porosity-permeability relationships[J]. AAPG bulletin, 2005, 89(4): 435-445. DOI: 10.1306/ 11230404071.
陈继良(1989-)男,硕士研究生,主要从事增强型地热系统地下物理过程的数值模拟研究。
蒋方明(1973-)男,博士,研究员,博士生导师,中国科学院广州能源研究所先进能源系统实验室主任, 先后工作于德国的 IMM 公司、葡萄牙的阿维诺(Aveiro)大学、美国的宾州州立大学, 2011 年 4 月获中国科学院“百人计划”引进海外杰出人才择优支持,主要从事电化学能量转化和存储、微尺度能量传递和转化、多尺度多物理数值模型等领域研究。
A Numerical Study on the Effect of Fluid-Rock Reaction during Enhanced Geothermal System Heat Extraction Processes
CHEN Ji-liang, HUANG Wen-bo, CAO Wen-jiong, JIANG Fang-ming
(Laboratory of Advanced Energy System, CAS Key Laboratory of Renewable Energy, Guangzhou Institute of Energy Conversion, Chinese Academy of Sciences, Guangzhou 510640, China)
Abstract:The enhanced geothermal system (EGS) circulates heat transfer fluid in the fracture network in the heat reservoir to extract heat from earth-deep hot dry rocks. During EGS operation, the heat transfer fluid may react with the rock in the heat reservoir. The dissolution/deposition of rock minerals dynamically changes the structure and morphology of fracture network in the reservoir, affecting the heat extraction process. This paper analyzes the characteristics of fluid-rock reaction in EGS reservoir, and details the method of coupling the fluid-rock reaction with thermo-fluid flow in porous medium, an equivalent model to the fractured rock reservoir. A Thermal-Hydraulic-Chemical (THC) model is established upon a previous numerical model developed by our group for heat and mass transport during EGS heat extraction processes. The new model is employed to study the long-term heat extraction process with respect to a quintuplet EGS (one injection well plus four production wells). Only interactions between water and calcite are considered in the simulation. The simulation result indicates the setting of injection temperature and mineral concentrations is crucial. If the two conditions cannot reach equilibrium state, the permeability and porosity around injection well will continually change, which will significantly affect the flow resistance of EGS reservoir.
Key words:enhanced geothermal systems (EGS); fluid-rock chemical reaction; numerical simulation
作者简介:
通信作者:†蒋方明,E-mail:jiangfm@ms.giec.ac.cn
基金项目:中科院百人计划(FJ);国家自然科学基金(51406213);NSFC-广东联合基金(U1401232);广东省自然科学基金重大基础培育项目(2014A030308001)
* 收稿日期:2015-09-06
修订日期:2015-11-23
文章编号:2095-560X(2016)01-0048-08
中图分类号:TK529;P314
文献标志码:A
doi:10.3969/j.issn.2095-560X.2016.01.008

