提升管管径对有机工质气泡泵性能的影响分析*
李华山,王令宝,卜宪标,马伟斌
(1. 中国科学院广州能源研究所,中国科学院可再生能源重点实验室,广州 510640;2. 中国科学院大学,北京 100049)
提升管管径对有机工质气泡泵性能的影响分析*
李华山1,2,王令宝1,2,卜宪标1†,马伟斌1
(1. 中国科学院广州能源研究所,中国科学院可再生能源重点实验室,广州 510640;2. 中国科学院大学,北京 100049)
摘 要:基于气液两相漂移流理论,对以TFE(三氟乙醇)/E181(四甘醇二甲醚)溶液为工质的扩散吸收式制冷系统气泡泵建立数学模型,通过MATLAB编程,在不同的浸没比和加热功率下,分析了提升管管径对TFE/E181气泡泵性能的影响规律。结果表明,TFE/E181气泡泵的性能随提升管管径的变化与浸没比和加热功率密切相关;在浸没比介于0.2 ~ 0.7,加热功率介于200 ~ 1 200 W的范围内,存在一个最佳的提升管管径使得气泡泵的溶液提升量与效率最大,且提升管最佳管径随着浸没比和加热功率的增大而增大,直至趋于弹状流最大许用直径;此外,当提升管管径一定的情况下,TFE/E181气泡泵的溶液提升量与效率随浸没比的增大而增大,而随加热功率的变化则与提升管管径的大小有关。
关键词:气泡泵;漂移流模型;提升管管径;浸没比;加热功率
0 引 言
近年来,随着经济发展,人们对低温的需求日益增多,制冷系统的能耗急剧上升。在此背景下,作为一种基于三元工质的热能驱动型制冷技术,扩散吸收式制冷系统得到相关研究人员的广泛关注[1]。扩散吸收式制冷系统无任何机械运动部件,且能够利用多种低品位能源如太阳能和余热等,是实现制冷环节节能降耗的重要补充。
气泡泵是扩散吸收式制冷系统的核心部件,用于将工质溶液提升至循环所需的高度,其性能对于制冷系统的效率与稳定运行均具有很大的影响。国内外相关研究人员针对气泡泵开展了大量的研究工作,如DELANO[2]分析了提升管管径、浸没比及加热功率等因素对气泡泵提升性能的影响,指出当提升管内流态为弹状流时,气泡泵的性能最佳,这一结论成为气泡泵设计的重要依据;WHITE[3]在气液两相流理论基础上分析比较了几种气泡泵模型,并对它们的适用范围进行了讨论;RATTNER等[4]从弹状流的机理出发建立了气泡泵数学模型,并与实验结果进行了对比验证;GUREVICH等[5]与陆引哲等[6]对多提升管式气泡泵进行了研究;陈永军等[7]通过实验分析了冷态工况下变截面管气泡泵的提升特性。总体来看,现有关于气泡泵的研究主要集中在结构形式、加热功率和加热方式等对气泡泵性能的影响几个方面。
目前扩散吸收制冷系统的循环工质以NH3/H2O为主,但NH3/H2O系统运行压力较高,需要精馏设备,且NH3毒性大、易爆且对常用金属材料有腐蚀性,在一定程度上限制了扩散吸收式制冷技术的发展与应用。因此,部分学者对多种不同新型工质的适用性进行了探索,以有机工质居多[8],其中TFE(三氟乙醇)/E181(四甘醇二甲醚)具有良好的热物理特性。与NH3/H2O工质相比,TFE/E181具有运行压力低,毒性小,且制冷剂与吸收剂之间的沸点差较大(200.3℃),系统无需精馏装置等优点[9]。这些优点使得TFE/E181溶液非常适宜作为吸收式系统的工作介质,研究人员对其应用于不同的吸收式系统进行了尝试,如MEDRANO等[10]和苏保国等[11]对以TFE/E181为工质的吸收式制冷循环进行了分析;CORONAS等[12]研究了以TFE/E181为工质的第一类吸收式热泵的性能;赵宗昌等[13-15]对单级、双效以及双吸收式TFE/E181第二类吸收式热泵的热力性能进行了研究。LONG等[16]和孟凡基等[17]从整体上对TFE/E181扩散吸收式制冷系统的研究表明,TFE/E181可以作为NH3/H2O的良好替代工质应用于扩散吸收式制冷系统,但他们未对TFE/E181气泡泵的性能进行详细研究。
文献调研表明,目前关于以TFE/E181为工质的气泡泵的研究非常有限。本文在漂移流模型理论的基础上,建立气泡泵数学模型,在不同的浸没比和加热功率下,研究提升管管径对TFE/E181气泡泵性能的影响规律,为TFE/E181气泡泵以及扩散吸收式制冷系统的设计提供理论依据。
1 气泡泵模型
气泡泵的结构如图1所示。定义系统液面气体压力为Psys,气泡泵提升管的管径(内径)为D,气泡泵发生器入口的管径(内径)为D0,气泡泵提升高度为L,气泡泵动力压头为H(贮液器液面到发生器之间的高度差)。
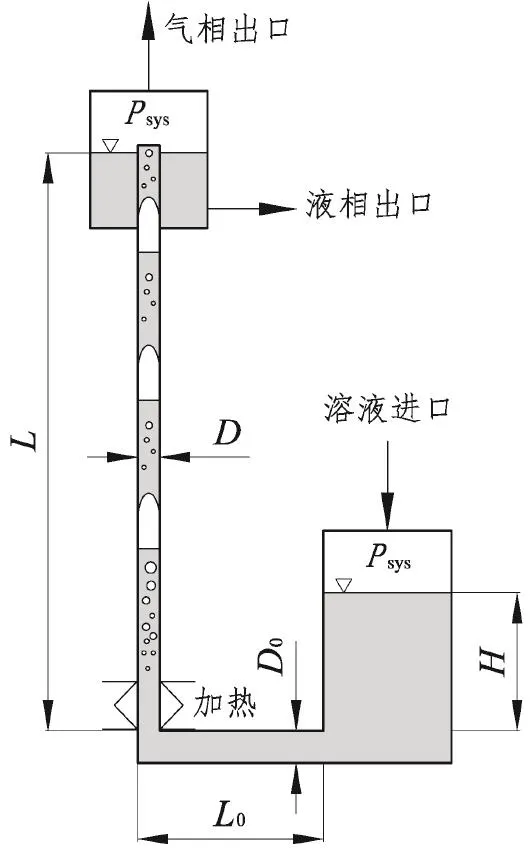
图1 气泡泵结构Fig. 1 Schematic diagram of bubble pump
为了简化计算,本文做如下假设:
(1)气泡泵提升管内流动为一维稳定绝热弹状流动;
(2)忽略气泡泵的散热损失;
(3)忽略水平管段到气泡泵提升管入口的阻力损失;
(4)气泡泵进出口的工质处于饱和状态[18-20];
(5)储液器液位高度保持不变。
根据质量守恒与动量守恒,气泡泵浸没比H/L与提升管内压力梯度的关系可以用数学公式描述如下[3]:
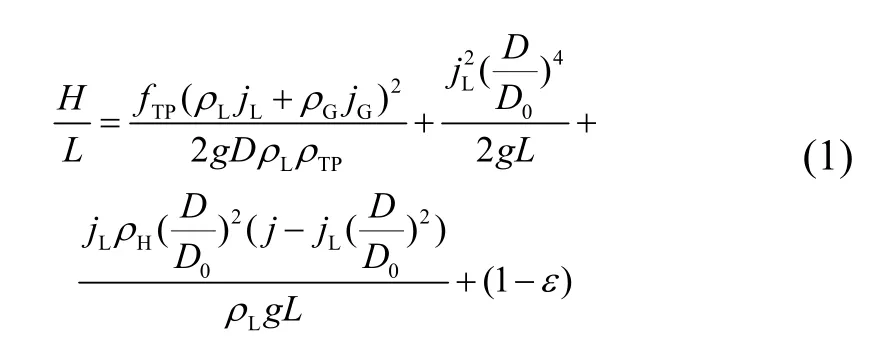
式中:fTP为两相流摩擦系数,ρTP为两相流密度,ρL为液相密度,ρG为气相密度,ρh为均相密度,jL为液相折算速度,jG为气相折算速度,ε为两相流空泡率。
两相流摩擦系数fTP由Colebrook-White公式计算[21]:

式中:fFan为范宁摩擦系数,ReTP为两相流雷诺数,εR为管壁粗糙度。
两相流雷诺数ReTP为:

两相流粘度μTP为:
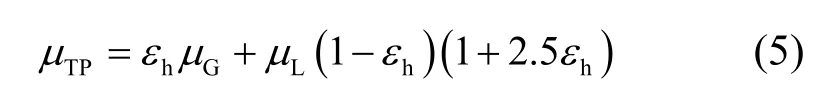
式中:μL为液相粘度,μG为气相粘度,εh为均相空泡率。均相空泡率εh计算如下
式中x为气相质量分数。
两相流密度ρTP为:

均相密度ρh为:

液相折算速度jL和气相折算速度jG分别为:

式中:mL与mG分别气泡泵出口液相和气相的质量流量;A为提升管截面积。
空泡率是决定气液两相流内部结构的基本参数,其计算模型主要有三大类,即滑速比模型、k·εh模型和漂移流模型[22],其中滑速比模型适用于两相间存在微弱耦合的场合,如分层流和环状流;k·εh模型适用于泡状流和雾状流;相对而言,漂移流模型具有较普遍的适用性,尤其在弹状流时使用这个模型结果相当好。本文中的两相流空泡率ε由ZUBER等[23]提出的漂移流模型计算:
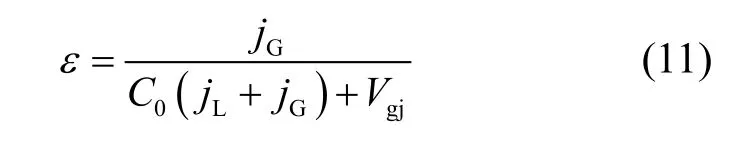
式中:C0为分布参数,Vgj为漂移速度。
根据WHITE[3]的推荐,C0和Vgj由DE CACHARD等[24]关联式计算:
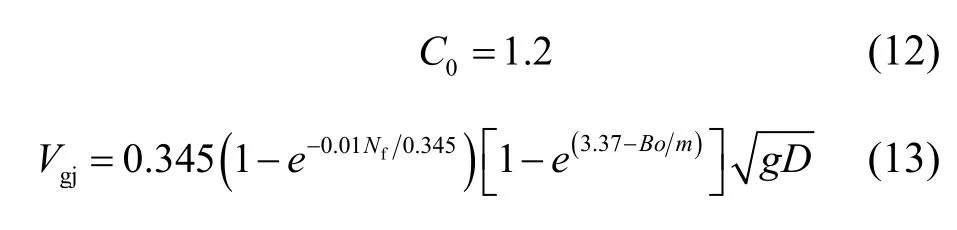
其中:
传说仙女下凡时,在辽阔的南中国海上撒下了一串串晶莹的珍珠,这就是美丽的南沙群岛。[一串串 晶莹的珍珠]

气泡泵的效率ηBP定义为单位加热量下气泡泵的溶液提升量,即:

式中:Q为加热功率,hLG为TFE的汽化潜热。
联立式(1)~ 式(17),并结合TFE/E181溶液的热物理特性参数,通过MATLAB软件编写程序进行求解,即可计算出给定的浸没比或加热功率下,TFE/E181气泡泵的效率以及溶液提升量随提升管管径的变化趋势。TFE/E181溶液以及制冷剂TFE的热物性根据HERRAIZ等[25]、徐士鸣等[9]、OGAWA 等[26]以及POLING等[27]给出的物性关系式计算。
2 模型验证
当气泡泵提升高度为0.5 m、运行压力400 kPa、发生温度375 K、进口NH3/H2O溶液浓度为15.5%、气泡泵溶液提升量为0.75 g/s时,针对浸没比H/L分别为0.4、0.6和0.8的工况进行计算,并与文献[3]进行对比,结果如图2所示。从图中可以看出本文的计算结果和文献[3]的结果吻合得很好,验证了计算模型的有效性。
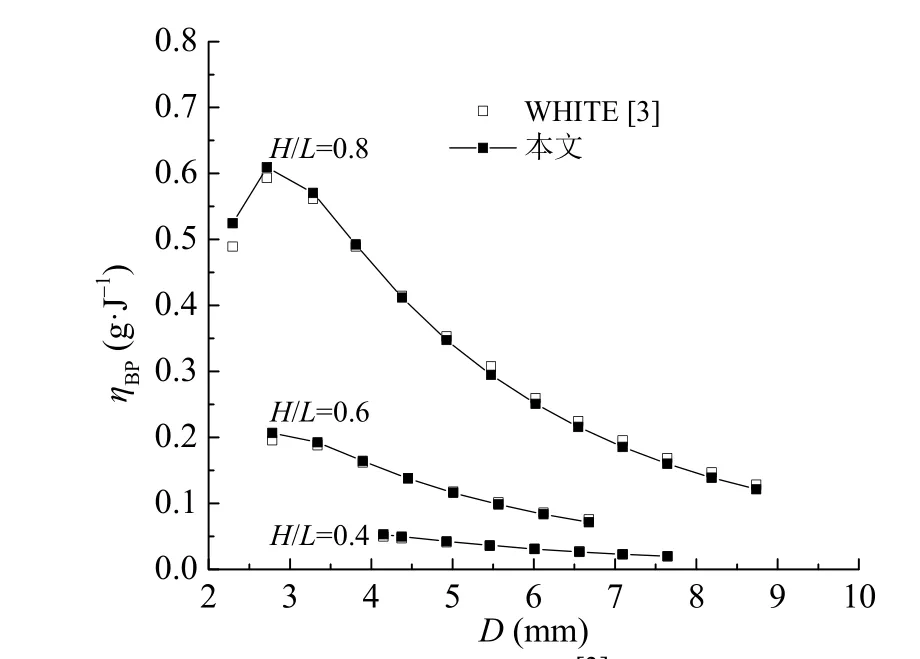
图2 模型计算结果与WHITE[3]对比Fig. 2 Model validation against WHITE[3]
3 结果与讨论
计算条件:气泡泵提升高度1.0 m,运行压力28 kPa(冷凝温度约45℃,空冷),进口TFE/E181溶液浓度为30%(发生温度约90℃,适宜太阳能以及其他低品位余热资源等开发利用)。在上述条件下,根据文献[28]给出的公式可以推算得到气泡泵产生弹状流的提升管最大许用直径约为25 mm。气泡泵溶液提升量与效率是表征气泡泵性能优劣的重要参数。本文在提升管管径D ≤ 25 mm的范围内,研究不同的浸没比与加热功率条件下提升管管径D对气泡泵溶液提升量mL与效率ηBP的影响。
3.1 浸没比恒定

图3 气泡泵溶液提升量随提升管直径的变化,H/L= 0.2Fig. 3 Bubble pump solution mass flow rate vs lift-tube diameter with H/L = 0.2
如图4所示,当浸没比恒定时,提升管管径对气泡泵效率的影响与其对气泡泵溶液提升量的影响基本一致。不同的加热功率下,气泡泵最大效率对应的管径与其出口的最大溶液提升量对应的管径相同。此外,在不同的加热功率下,虽然气泡泵的溶液提升量变化很大,但其最大效率却变化很小。如当气泡泵浸没比为0.2,加热功率从200 W升至1 200 W时,气泡泵的最大效率仅介于0.038 ~ 0.041 g·J−1,说明在浸没比一定的情况下,加热功率对改善气泡泵的极限输送效率作用非常有限。

图4 气泡泵效率随提升管直径的变化,H/L = 0.2Fig. 4 Bubble pump efficiency vs lift-tube diameter with H/L = 0.2
3.2 加热功率恒定
当加热功率恒定(Q = 200 W)时,在不同的浸没比下,气泡泵溶液提升量随提升管管径的变化如图5所示。从图中可以看出,在一定范围内,随着提升管管径的增大,气泡泵溶液提升量呈先增加后减小的趋势,但当气泡泵浸没比大于一定值以后,随着提升管管径的增大,气泡泵溶液提升量持续增大,直至弹状流最大许用直径。此外,浸没比越大,气泡泵的溶液提升量也越大,且最大溶液提升量对应的最佳提升管管径也越大。这是因为在气泡泵高度不变的情况下,随浸没比H/L的增大,气泡泵动力压头H增大,而净提升管高度(L – H)降低,较大驱动力更容易实现较小的净提升高度,从而使得气泡泵的溶液提升量增加。
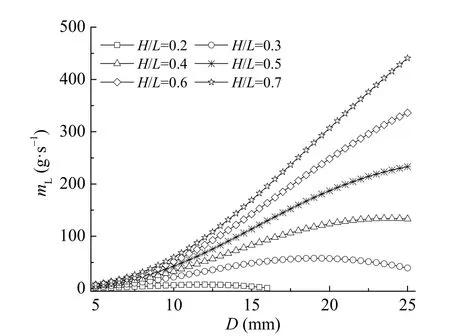
图5 气泡泵溶液提升量随提升管直径的变化,Q = 200 WFig. 5 Bubble pump solution mass flow rate vs lift-tube diameter with Q = 200 W

图6 气泡泵效率随提升管直径的变化,Q = 200 WFig. 6 Bubble pump efficiency vs lift-tube diameter with Q = 200 W
从图6可以看出,在加热功率恒定的情况下,随着提升管管径的增大,当浸没比相对较小时,气泡泵的效率呈先增加后减小的趋势,但当浸没比较大时,随着提升管管径的增加,气泡泵的效率逐步升高。此外,在提升管管径固定的情况下,随着浸没比的增大,气泡泵的效率逐步增大,且提升管管径越大增幅越大。如当D = 15 mm时,H/L = 0.4的气泡泵效率较H/L = 0.3的效率高71%左右,而当D = 20 mm时,这一比例升至115%。这一现象说明浸没比对于提高气泡泵性能起着关键作用。因而,在符合设计要求的条件下,应尽可能地增大气泡泵的浸没比以获得较高的效率。
4 结 论
本文在TFE/E181溶液浓度为30%、运行压力28 kPa、浸没比介于0.2~0.7以及加热功率介于200~1 200 W的条件下,研究了提升管管径对TFE/E181气泡泵性能的影响,结果表明:
(1)浸没比恒定的情况下,随着提升管管径的增大,气泡泵的溶液提升量及效率均呈先增加后减小的趋势。
(2)加热功率恒定的情况下,随着提升管管径的增大,当浸没比较小时,气泡泵的溶液提升量及效率均呈先增大后减小趋势,但当浸没比较大时,气泡泵的溶液提升量及效率则持续升高。
(3)气泡泵提升管的最佳管径与浸没比与加热功率密切相关,随着浸没比与加热功率的增大,最佳管径逐渐增大,直至趋于弹状流最大许用直径。
(4)此外,在提升管管径固定的情况下,气泡泵的溶液提升量及效率随浸没比的增大而增大,但随加热功率的变化因管径大小而呈现差异。
参考文献:
[1] 曹园树, 李华山, 龙臻, 等. 扩散吸收式制冷技术进展[J]. 新能源进展, 2014, 2(1): 63-69. DOI:10.3969/ j.issn.2095-560X.2014.01.011.
[2] DELANO A D. Design analysis of the Einstein refrigeration cycle[D]. Atlanta: Georgia Institute of Technology, 1999.
[3] WHITE S J. Bubble pump design and performance[D]. Atlanta: Georgia Institute of Technology, 2001.
[4] RATTNER A S, GARIMELLA S. Coupling-fluid heated bubble pump generators: experiments and model development[J]. Science and technology for the built environment, 2015, 21(3): 332-347. DOI: 10.1080/ 10789669.2015.1004978.
[5] GUREVICH B, JELINEK M, LEVY A, et al. Performance of a set of parallel bubble pumps operating with a binary solution of R134a-DMAC[J]. Applied thermal engineering, 2015, 75: 724-730. DOI: 10.1016/j.applthermaleng.2014.09.074.
[6] 陆引哲, 刘道平, 徐煌栋. 多管式气泡泵设计[J]. 热能动力工程, 2015, 30(2): 212-217.
[7] 陈永军, 刘道平, 眭阳, 等. 冷态工况下变截面管气泡泵提升特性试验研究[J]. 流体机械, 2015, 43(3): 47-51, 82. DOI: 10.3969/j.issn.1005-0329.2015.03.010.
[8] RODRÍGUEZ-MUÑOZ J L, BELMAN-FLORES J M. Review of diffusion-absorption refrigeration technologies[J]. Renewable and sustainable energy reviews, 2014, 30: 145-153. DOI: 0.1016/j.rser.2013.09.019.
[9] 徐士鸣, 任国红, 陈石. TFE-TEGDME吸收式制冷/热泵工质热物性参数表达式[J]. 大连理工大学学报, 2002, 42(1): 60-64. DOI: 10.3321/j.issn:1000-8608.2002. 01.015.
[10] MEDRANO M, BOUROUIS M, CORONAS A. Double-lift absorption refrigeration cycles driven by low-temperature heat sources using organic fluid mixtures as working pairs[J]. Applied energy, 2001, 68(2): 173-185. DOI: 10.1016/S0306-2619(00)00048-9.
[11] 苏保国, 任国红, 宋振寰. 以TFE-TEGDME为工质的制冷循环分析[J]. 制冷技术, 2003(1): 25-28.
[12] CORONAS A, VALLÉS M, CHAUDHARI S K, et al. Absorption heat pump with the TFE-TEGDME and TFE-H2O-TEGDME systems[J]. Applied thermal engineering, 1996, 16(4): 335-345. DOI: 10.1016/ 1359-4311(95)00007-0.
[13] 赵宗昌, 周方伟, 李凇平. TFE-E181高温型第二类吸收式热泵热力过程分析[J]. 大连理工大学学报, 2004, 44(5): 651-656. DOI: 10.3321/j.issn:1000-8608.2004.05.006.
[14] ZHAO Z C, ZHANG X D, MA X H. Thermodynamic performance of a double-effect absorption heattransformer using TFE/E181 as the working fluid[J]. Applied energy, 2005, 82(2): 107-116. DOI: 10.1016/ j.apenergy.2004.10.012.
[15] 赵宗昌, 周方伟, 李凇平. TFE-E181双吸收热变换器热力过程分析[J]. 大连理工大学学报, 2003, 43(5): 604-608. DOI: 10.3321/j.issn:1000-8608.2003.05.014.
[16] LONG Z, LUO Y, LI H S, et al. Performance analysis of a diffusion absorption refrigeration cycle working with TFE-TEGDME mixture[J]. Energy and buildings, 2012, 58: 86-92. DOI: 10.1016/j.enbuild.2012.12.003.
[17] 孟凡基, 龙臻, 李华山, 等. TFE-TEGDME-He扩散-吸收式制冷系统实验研究[J]. 低温与超导, 2014, 42(6): 58-62, 67.
[18] BENHMIDENE A, CHAOUACHI B, GABSI S, et al. Modeling of boiling two-phase flow in the bubble pump of diffusion-absorption refrigeration cycles[J]. Chemical engineering communications, 2015, 202(1): 15-24. DOI: 10.1080/00986445.2013.828608.
[19] JO S W, SHERIF S A, LEAR W E. Numerical simulation of saturated flow boiling heat transfer of ammonia/water mixture in bubble pumps for absorption-diffusion refrigerators[J]. Journal of thermal science and engineering applications, 2014, 6(1): 011007. DOI: 10.1115/1.4025091.
[20] 叶鹏, 刘道平, 梁俣. 单压吸收式制冷系统气泡泵理论模型与验证[J]. 低温与超导, 2013, 41(12): 79-82. DOI: 10.3969/j.issn.1001-7100.2013.12.018.
[21] BEATTIE D R H, WHALLEY P B. A simple two-phase frictional pressure drop calculation method[J]. International journal of multiphase flow, 1982, 8(1): 83-87. DOI: 10.1016/0301-9322(82)90009-X.
[22] 孙奇, 赵华, 杨瑞昌, 等. 垂直上升两相流漂移流模型研究[J]. 核动力工程, 2006, 27(2): 40-44. DOI: 10.3969/j.issn.0258-0926.2006.02.010.
[23] ZUBER N, FINDLAY J A. Average volumetric concentration in two-phase flow systems[J]. Journal of heat transfer, 1965, 87(4): 453-468. DOI: 10.1115/ 1.3689137.
[24] DE CACHARD F, DELHAYE J M. A slug-churn flow model for small-diameter airlift pumps[J]. International journal of multiphase flow, 1996, 22(4): 627-649. DOI: 10.1016/0301-9322(96)00003-1.
[25] HERRAIZ J, OLIVÉ F, ZHU S M, et al. Thermophysical properties of 2, 2, 2-trifluoroethanol+tetraethylene glycol dimethyl ether[J]. Journal of chemical & engineering data, 1999, 44(4): 750-756. DOI: 10.1021/je980284r.
[26] OGAWA K, ISSHIKI N, KOGA H, et al. Measurement of surface tension of TFE/E181 and TFE/NMP binary systems[C]//2nd pacific Asia conference on mechanical engineering. Manila Philippines, 1998: 639-647.
[27] POLING B E, PRAUSNITZ J M, O’CONNELL J P. 气液物性估算手册[M]. 赵红玲, 王凤坤, 陈圣坤, 等译.北京: 化学工业出版社, 2006.
[28] 陈学俊, 陈立勋, 周芳德. 气液两相流与传热基础[M].北京: 科学出版社, 1995.
李华山(1981-),男,博士研究生,助理研究员,主要从事低焓热能利用技术研究。
卜宪标(1979-),男,博士,副研究员,硕士生导师,主要从事余热利用技术、中低温地热发电技术等方面的研究。
Effects of Lift-tube Diameter on Performance of Bubble Pump with Organic Working Fluids
LI Hua-shan1,2, WANG Ling-bao1,2, BU Xian-biao1, MA Wei-bin1
(1. CAS Key Laboratory of Renewable Energy, Guangzhou Institute of Energy Conversion, Chinese Academy of Sciences, Guangzhou 510640, China; 2. University of Chinese Academy of Sciences, Beijing 100049, China)
Abstract:As a key component in diffusion absorption refrigeration systems, the bubble pump is the motive force and has great effect on the performance and stable operation of the refrigeration unit. Based on drift-flux model, a mathematical model for the bubble pump in the diffusion absorption refrigeration system is established under MATLAB. TFE (2,2,2-trifluoroethanol)/E181 (tetraethylene glycol dimethyl ether) mixture is used as working fluids. The effects of the lift-tube diameter on the TFE/E181 bubble pump performance, including solution mass flow rate and efficiency, were investigated under different submergence ratio and heating power. The results show that the TFE/E181 bubble pump performance changing with the lift-tube diameter is closely linked to the submergence ratio and heating power. When the submergence ratio ranges from 0.2 to 0.7 and heating power is between 200 W and 1200 W, there exists an optimum diameter for the lift-tube that can make the solution mass flow rate as well as efficiency of the bubble pump maximum. With the submergence ratio and heating power increased, the optimum diameter increases till it reaches slug flow’s limitation. In addition, for the lift-tube with a certain diameter, the solution mass flow rate and efficiency of the TFE/E181 bubble pump increase with the increase in the submergence ratio, but their variation trends with the increased heating power depend on the size of lift-tube diameter.
Key words:bubble pump; drift-flux model; lift-tube diameter; submergence ratio; heating power
作者简介:
通信作者:†卜宪标,E-mail:buxbz@ms.giec.ac.cn
基金项目:国家自然科学基金项目(51106161);广东省科技计划项目(2013B010405013);中国科学院可再生能源重点实验室基金项目(y507j71001)
* 收稿日期:2015-11-15
修订日期:2015-12-07
文章编号:2095-560X(2016)01-0056-06
中图分类号:TK122
文献标志码:A
doi:10.3969/j.issn.2095-560X.2016.01.009

