一种新的平移不变Shearlet变换域图像去噪算法

石满红，刘 卫



一种新的平移不变Shearlet变换域图像去噪算法

石满红1，刘 卫2

（1. 安徽科技学院信息与网络工程学院，安徽 凤阳 233100；2. 中国科学院合肥智能机械研究所，安徽 合肥 230031）

提出了一种基于双边滤波和正态逆高斯模型的平移不变Shearlet变换域图像去噪算法。对图像进行平移不变Shearlet变换分解，低频子带采用快速双边滤波算法处理，高频子带采用正态逆高斯模型对其进行建模，在贝叶斯最大后验概率估计准则下推导出与正态逆高斯模型相对应的阈值函数表达式，从而达到去除图像噪声的目的。在对不同类型的图像进行仿真实验，其结果表明了本文方法不仅具有良好的视觉效果，而且具有较高的峰值信噪比和平均结构相似性。

图像去噪；平移不变Shearlet变换；双边滤波；正态逆高斯模型；贝叶斯估计

0 引言

图像在采集和传输的过程中会不可避免地受到噪声污染，噪声的存在降低了图像的分辨率。因此，如何有效的去除噪声，成为了图像处理中的经典问题。传统的图像去噪方法主要有空域低通滤波、统计滤波及频域滤波等，虽然这些方法对噪声有一定的抑制效果，但是损失了图像的许多细节信息，会造成去噪图像模糊，产生振铃现象。小波变换具有良好的时频域局部化性质，基于小波变换域的图像去噪方法，能够较好地保持图像的细节信息，成为目前常用的去噪方法之一。小波域图像去噪方法中最为著名的是Donoho[1]提出的全局阈值收缩去噪方法，阈值方法实现简单且可达到一定的降低噪声的效果，因而引起学者们的广泛关注。传统的阈值方法并未考虑各尺度内小波系数的相关性，而小波系数之间具有较强的相关性，因此学者们提出多种小波系数的先验统计模型，以便获得更好的去噪效果。Crouse等人[2]提出了隐马尔科夫树模型去噪算法，该算法时间复杂度太高且噪声无法达到有效去除，2000年Chang等人[3]提出了基于广义高斯分布模型Bayes Shrink去噪算法，但丢失过多的高频系数，使得去噪效果不理想。2002年，Sendur等人利用小波系数尺度间的相关性，提出BiShrink[4]和Local-BiShrink[5]去噪方法，其主要是用二元非高斯分布来充分体现小波系数尺度间的相关性并作为先验分布，实验显示基于二元非高斯分布模型去噪效果要好于广义高斯分布模型及隐马尔可夫模型，但去噪效果无法进一步得到提升。文献[6]用有限高斯混合模型来逼近小波系数分布，这些方法在一定程度上改善了去噪效果，但仍存在较大的局限性，例如缺乏局部自适应性。2005年Cho提出了多元广义高斯分布模型[7]，该模型通过调整不同的参数可以包含Gaussian、GGD、Non-Gaussian等模型，但是去噪过程中参数的估计比较复杂。2010年，郭强等人提出了Shearlet变换域的三变量模型的图像去噪方法[8]，但是估计结果需要用到迭代算法，复杂度较高。2014年，刘炳良[9]提出结合小波变换和双边滤波相结合的去噪算法，虽然取得了不错的效果，但是其并未考虑到低频子带中的噪声。Barndorff-nielesn[10]提出的正态逆高斯（NIG）模型，该模型能够描述任意形状的曲线，因而可以对不同程度拖尾的图像分解系数进行准确建模，因此其作为图像分解系数的先验模型是合适的。

随着小波变换的局限性（缺乏多方向选择性和非稀疏性）日益显现，学者们提出了多尺度几何分析方法[11-13]。2007年Guo等人[13]提出了一种新的多尺度几何分析方法——Shearlet变换，它能够对图像进行稀疏表示且产生最优逼近。与传统的多尺度分析方法相比Shearlet没有方向数和支撑尺寸大小的限制，Shearlet可以通过一个基函数的膨胀、剪切和平移变换来进行构造的。此外，Shearlet逆变换时只需要对正向变换中的剪切滤波器进行加工和处理，因而Shearlet实现过程具有更高的计算效率。由于Shearlet具有以上这些优点，其已应用于许多图像处理领域，如图像去噪[14]、边缘检测[15]、图像融合[16-18]等。然而，由于Shearlet离散化过程中也采用了下采样操作，因而其不具备平移不变性，应用于图像去噪时易在奇异点附近产生伪吉布斯现象。平移不变Shearlet变换[15]通过级联非下采样金字塔滤波器和剪切滤波器，其具有Shearlet变换的所有优点且实现过程没有采用下采样操作，因而其具有平移不变性，所以平移不变Shearlet变换更适合于图像去噪工作。

噪声图像经多尺度几何变换后，虽然噪声大部分集中高频子带，但是其低频子带仍存在一部分噪声。本文在此基础上提出了一种基于快速双边滤波[19]和正态逆高斯模型的平移不变Shearlet变换域图像去噪算法，将平移不变Shearlet与正态逆高斯模型相结合，采样快速双边滤波算法处理低频子带，以正态逆高斯模型为高频系数的先验模型，利用贝叶斯最大后验概率估计准则，以达到去除噪声的目的。实验结果表明该方法能够取得较好地去噪效果。

1 基于正态逆高斯模型的平移不变Shearlet变换域图像去噪算法

1.1 Shearlet变换

Guo和Labate[13]在合成小波理论基础上衍生出Shearlet变换。当维数＝2时，具有合成膨胀的仿射系统定义为：

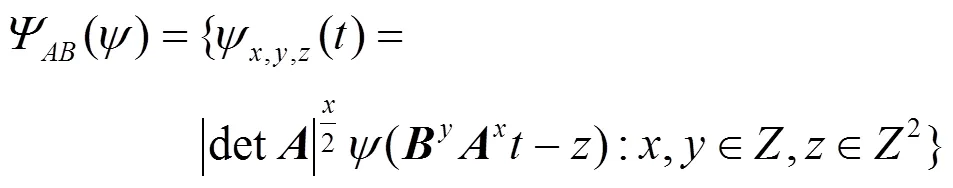
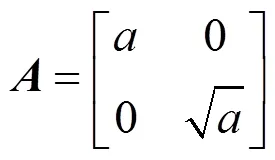
则对于任意的∈＋，∈，∈2，Shearlet基函数定义为：

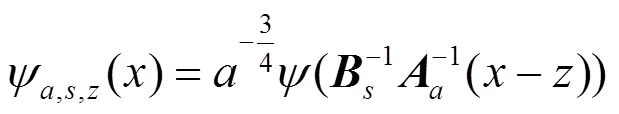
基于以上Shearlet定义，函数()的Shearlet变换为：

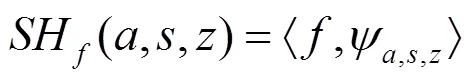
式中：,,分别表示图像尺度参数、剪切方向和平移量。Shearlet变换的频域支撑如图1所示。

SIST用于图像处理时，需采用离散化形式，离散化过程主要分为两步：①首先对图像利用非下采样金字塔滤波器组进行多尺度分解，图像经过级非下采样金字塔滤波器，可以得到＋1个与原图像大小相同的子带图像。②对得到的各尺度子带图像使用剪切滤波器组进行方向分解。经以上两个步骤完成了SIST对图像的分解。由于在图像处理的过程中没有进行采样操作，使其具有平移不变性。更多关于SIST可以参考文献[15]。

1.2 SIST变换域图像去噪算法

以往基于小波变换域的图像去噪算法，大多只是处理其高频子带，而认为低频子带中不含有噪声。实际研究发现，含噪图像经过小波分解，噪声虽然主要集中于高频子带，但其低频子带中仍存在少量噪声，如果仅仅处理高频子带，那么处理后的图像视觉效果不佳，因而在设计图像去噪算法时应考虑低频子带的噪声情况。因此本文对图像进行SIST分解后，为了减少计算负担，首先对低频子带采用快速双边滤波[19]处理，然后对高频子带用NIG模型进行建模，再进行后续的处理。

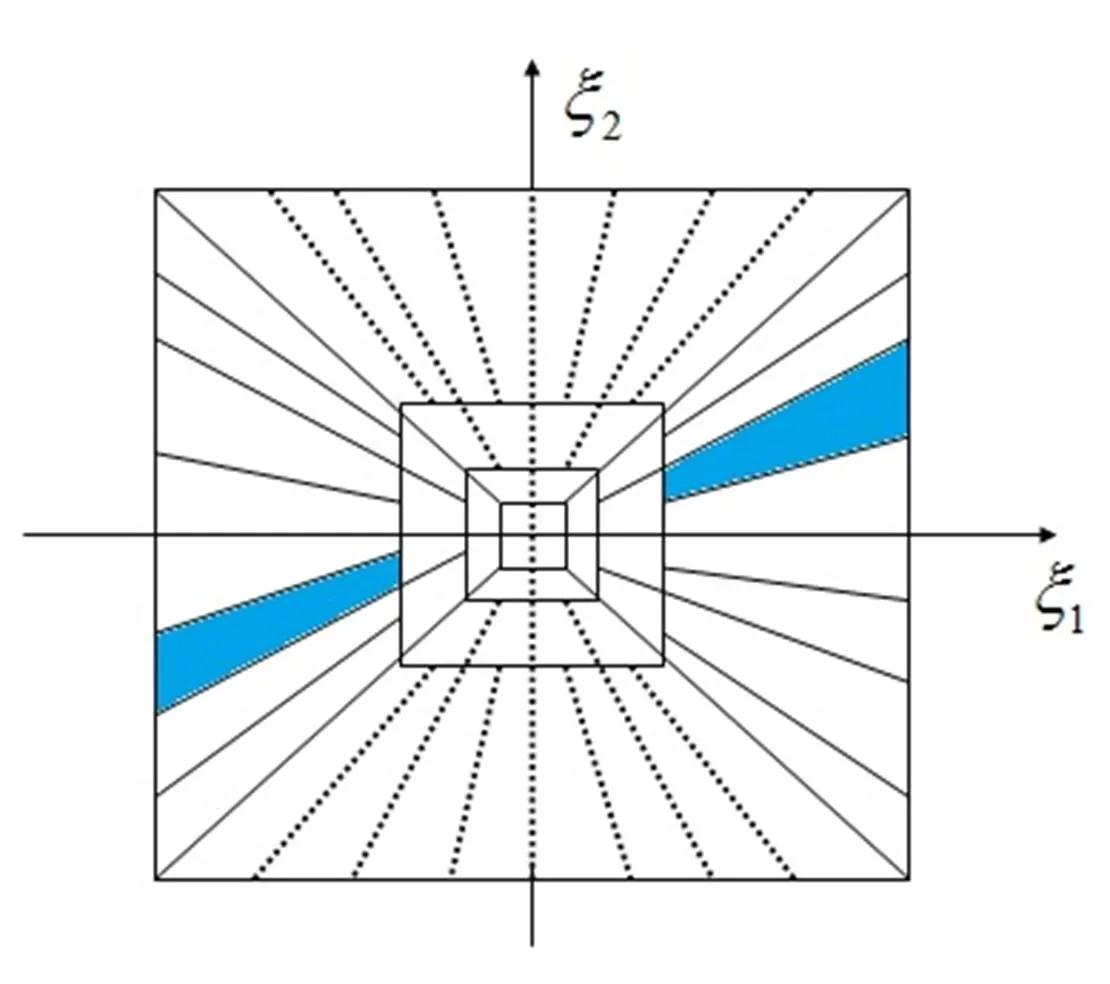
图1 Shearlet变换频域支撑

1.2.1 NIG模型

基于统计模型的小波变换域图像去噪算法，通常都需要知道图像的小波变换系数的概率密度函数，然而对于一幅自然图像，其变换系数的概率密度函数是无法准确确定的，通常需要使用经验直方图来近似获得。图像经小波变换后，其系数具有零均值，重拖尾的特点，因而Gaussian[20]、Generalized Gaussian Distribution[3]等模型都曾被用来模拟其分布情况，然而小波系数的实际分布情况与这些模型却有些区别，通过大量实验我们发现SIST变换系数也具有小波系数的分布特点。文献[9]提出了一个混合模型，它由一个逆高斯分布和一个具有不同均值的高斯分布组成。由于其参数具有很强的灵活性，理论上可以描述任何形状的曲线，因而可以作为SIST变换系数的先验分布，其概率密度函数为：

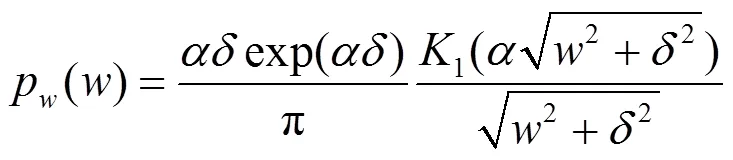
为了检验使用正态逆高斯分布作为SIST系数的分布的先验模型的合理性，我们分别使用纹理较为丰富的图像（Barbara）及纹理较少、对比度较低的红外图像（Plane）作为拟合示例，图2是分别用NIG和GGD来拟合Barbara图像及Plane图像经2层SIST分解（方向数为4，4）的第二层四个方向的系数分布。从图2中我们可以看出，GGD无法很好地拟合原始系数的经验分布，而NIG可以准确地对原始系数分布进行拟合，这种高度拟合情形也同样出现在其他的子带中，这再次证明了我们假定NIG为图像的系数分布的合理性。

1.2.2 贝叶斯最大后验概率估计

通常情况下，图像的退化模型可以简化为：

＝＋(5)

式中：为原始图像；为均值为零、方差为2的服从高斯分布的噪声；为含噪图像。

经SIST变换后，得到：

＝＋(6)

由上假定噪声服从高斯分布，则高斯白噪声概率密度函数为：

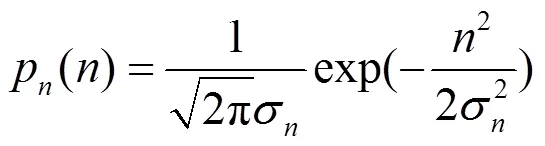
令(7)式右边的一阶导数等于零，并将(4)和式(8)代入式(7)，从而得到原始系数的估计解：

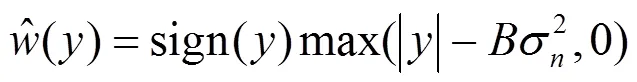
利用式(9)对图像进行去噪处理时，需要估计出正态逆高斯模型的参数、以及噪声方差2，参数、根据不同子带系数自适应的估计出来，因而可以自适应的处理噪声图像的分解系数。

1.2.3 模型参数估计

对各个子带内对应的噪声方差2本文采用蒙特卡洛[2]方法进行估计。参数、可以利用下式进行估计：

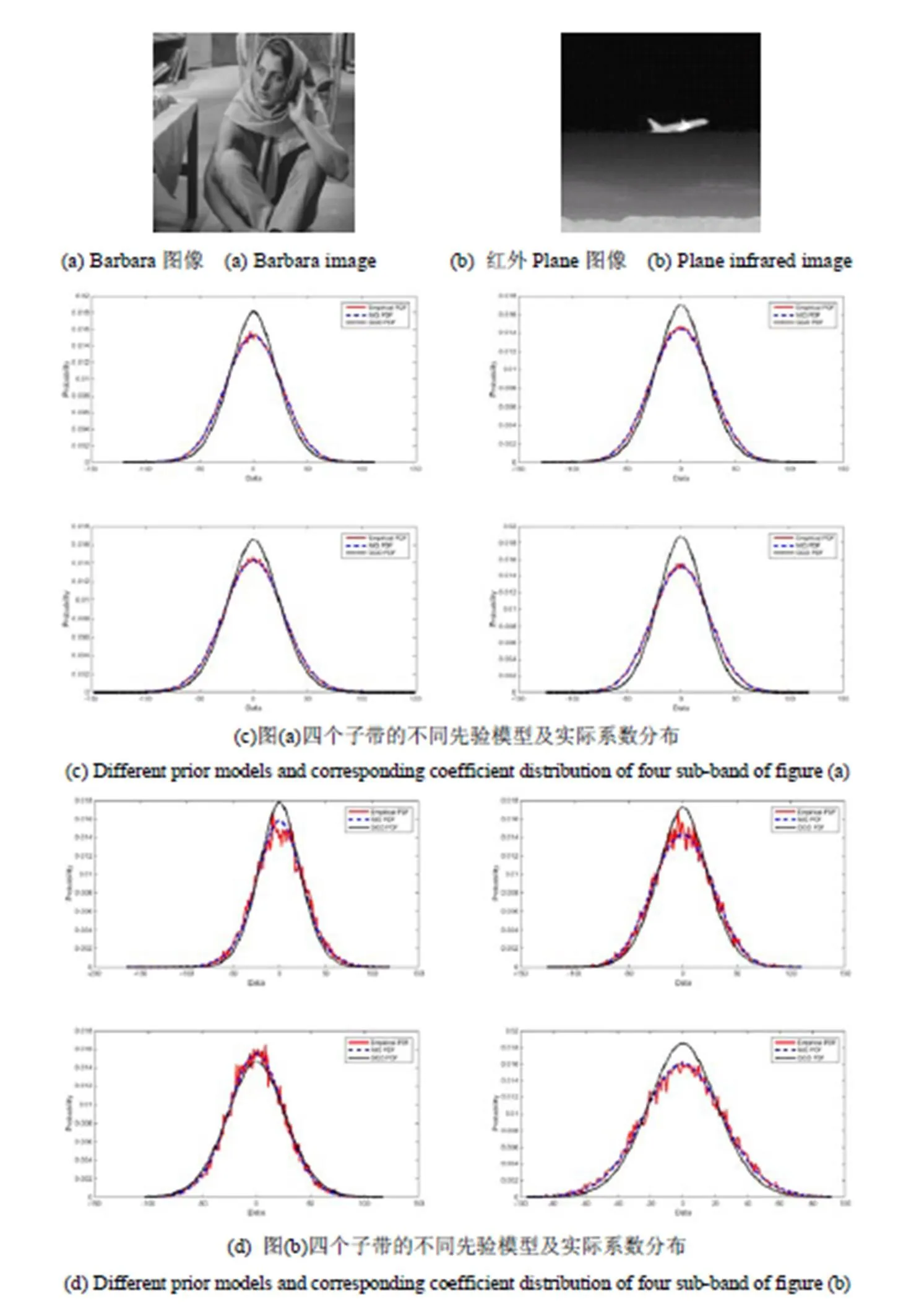
图2 不同先验模型对实际分解系数分布的拟合示意图

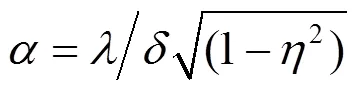
1.2.4 算法主要步骤

Step1：对含噪图像先进行四层SIST变换，方向数由粗到细尺度的方向数依次为4, 8, 8, 16，得到低通子带和一系列带通子带；

Step2：采样快速双边滤波算法处理低频子带；

Step3：运用蒙特卡罗方法估计各个子带的噪声方差2，再利用式(10)、(11)对每个子带估计正态逆高斯模型的参数、；

Step5：进行逆SIST变换，从而得到去噪图像。

2 实验结果与分析

在仿真实验中，对自然图像Lena、Barbara、Peppers、红外图像Plane及遥感图像（Pentagon）进行测试，加入零均值、方差为2的高斯白噪声。将本文所提的去噪算法与Contourlet变换（CT）[11]的硬阈值算法，Mihcak等[20]人提出的LAWML（5×5）算法，非下采样Contourlet变换[12]（NSCT）算法、基于双树复小波（DTCWT）的双变量收缩（BiShrink）[5]算法以及SURE-LET[21]进行比较；然后峰值信噪比（PSNR）、平均结构相似性[22]（MSSIM）以及去噪后的视觉效果结合起来评价本文方法。其中峰值信噪比定义为：

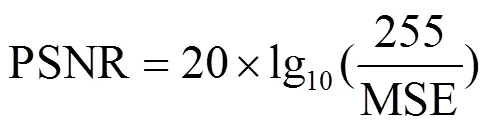
从表1中可以看出，各种方法去噪后的PSNR均有不同程度的提高，这说明了几种方法的有效性；其中本文的去噪方法处理后的PSNR相比其他方法是最高的。相比于CT方法的去噪效果有明显的优势；与LAWML及SURE-LET方法相比，本文方法获得的PSNR值有较大的提高，平均提高在1.3dB以上；相比于其他两种去噪方法，本文方法去噪后的PSNR也有不同幅度的提升。

从图3、4中可以看出，BiShrink方法使用了二元收缩方法，去噪后零系数太多，细节丢失严重，使得去噪后的图像过于平滑，LAWML方法获得的图像毛刺现象较为严重，本文去噪算法保留了图像大部分的细节信息，如桌面纹理清晰可见，图像视觉效果更好，与NSCT算法相比也有一定的程度上的改善；从图5、6可以看出，Contourlet变换域硬阈值去噪后的图像存在振铃现象，LAWML和BiShrink方法去噪后的图像整体偏暗，边缘变得模糊，本文方法处理后的图像减少了振铃现象，图像更清晰。

此外，本文方法不仅具有更好的视觉效果和较高的峰值信噪比，从表2可以看出，本文去噪后平均结果相似性也是最高的，表明本文方法去噪后的图像保持原图像的结构能力要高于其他方法。

3 结论

本文充分考虑了含噪图像经SIST分解后，其高、低频子带中的噪声情况，在SIST变换域中，提出了基于双边滤波和正态逆高斯模型的SIST变换图像去噪算法。快速双边滤波算法用来处理低频子带，消除了低频子带中的噪声，以NIG为先验模型对高频进行建模，由于模型的参数的自适应性，使得去噪阈值具有自适应性，改善了去噪效果。仿真实验表明，本文算法无论是在主观视觉效果还是客观评价标准PSNR、MSSIM上都有明显的提高和改善，在有效去除噪声的同时，更好的保持了原图像的细节信息，证明本文算法的有效性。

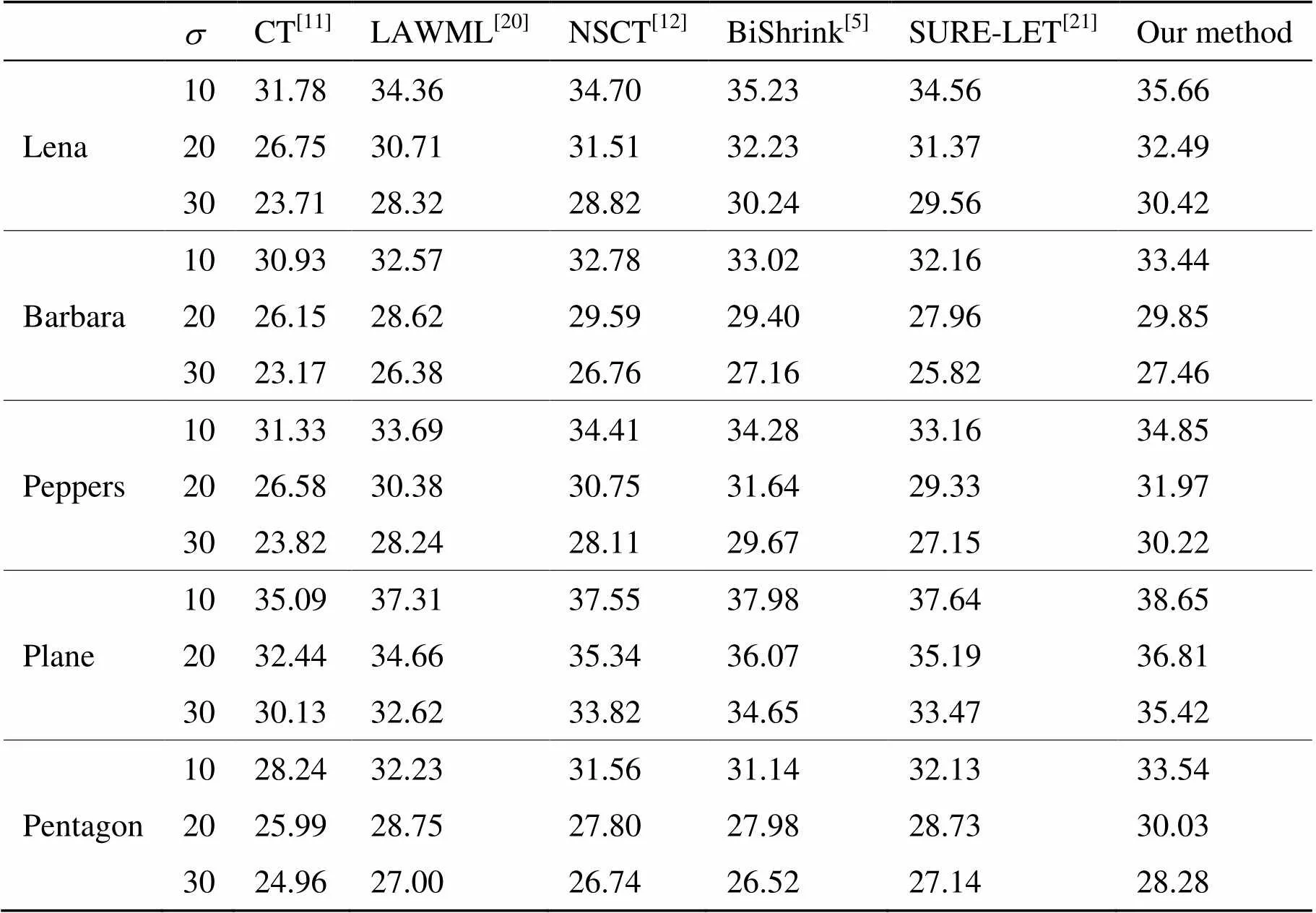
表1 不同方法去噪后的峰值信噪比（PSNR）

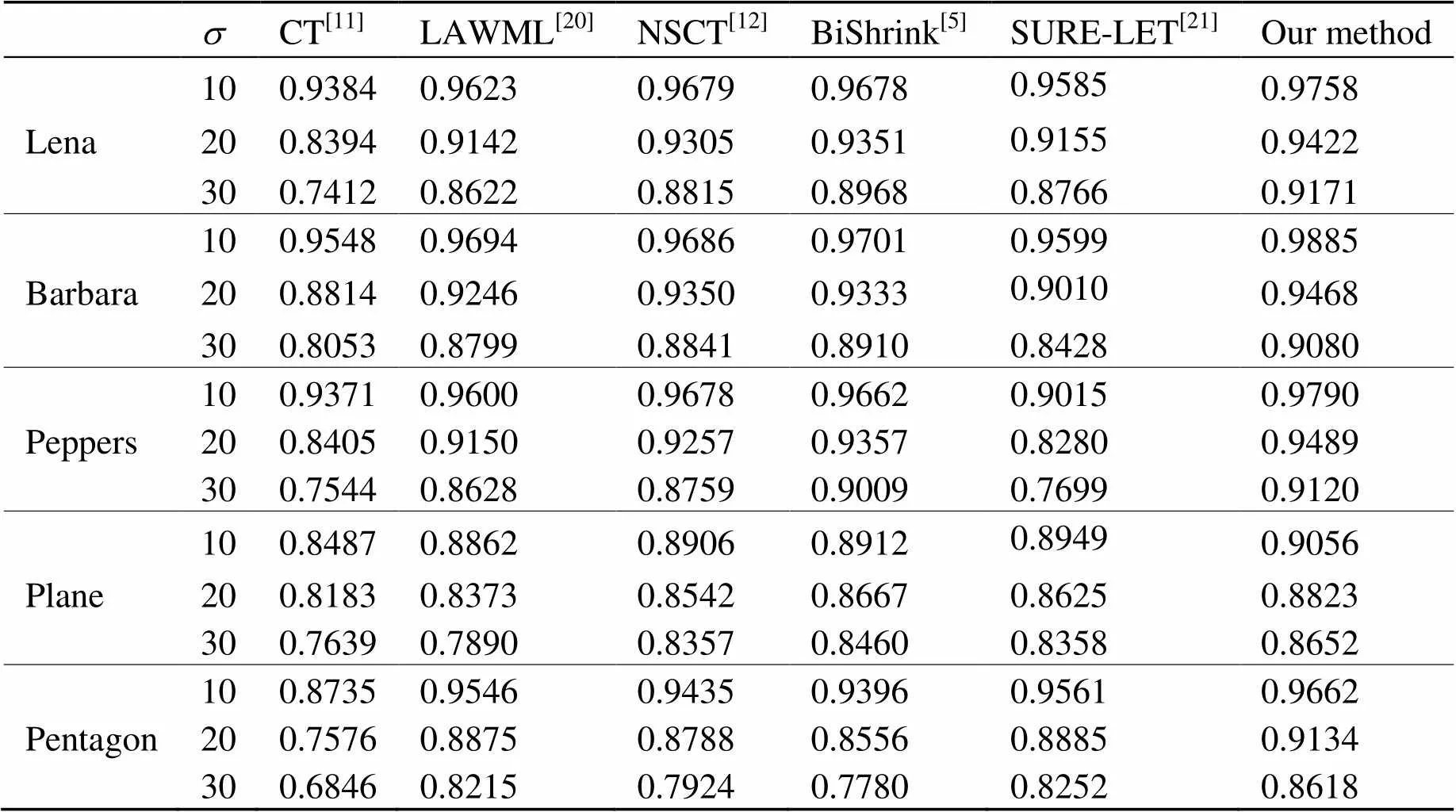
表2 不同方法去噪后的平均结构相似性比较（MSSIM）

图3 噪声方差为20的图像（Barbara）去噪后局部放大图

图4 不同方法去噪后的图像（Peppers）比较（噪声标准差为20）

图5 不同方法去噪后的红外图像（Plane）比较（噪声标准差为20）

图6 不同方法去噪后的遥感图像（Pentagon）比较（噪声标准差为20）

[1] Donoho D L. Denoising by soft-thresholding [J]., 1995, 41(3): 613-627.

[2] Crouse M. S, Nowak R D, Baraniuk R G. Wavelet-based statistical signal processing using hidden Markov models[J]., 1998, 46(4): 886-902.

[3] Chang S, Yu B, Vetterli M. Adaptive wavelet thresholding for image denoising and compression[J]., 2000, 9(9): 1532-1546.

[4] Sender L, Selesnick I W. Bivariate shrinkage functions for wavelet- Based denoising exploiting interscale dependency[J]., 2002, 20(11): 2744-2756.

[5] Sender L, Selesnick I W. Bivariate shrinkage with local variance estimation[J]., 2002, 9(12): 438-441.

[6] Portilla J, Strla V. Image denoising using scale mixtures of Gaussians in the wavelet domain[J]., 2003, 12(11): 1338-1351.

[7] Cho D, Bui T D. Multivariate statistical modeling for image denoising using wavelet transforms[J]., 2005, 20(1): 77-89.

[8] 郭强, 郁松年. 基于三变量模型的剪切波去噪方法[J]. 自动化学报, 2010, 36(8): 1062-1072.

GUO Qiang, YU SongNian. Shearlet-based Image Denoising Using Trivariate Prior Model[J]., 2010, 36(8): 1062-1072

[9] 刘炳良. 一种小波域改进双边滤波的水果图像去噪算法[J]. 红外技术, 2014, 36(3): 196-199.

LIU Bingliang. A new improved bilateral filtering algorithm for the fruit image based on wavelet transform domain[J]., 2014, 36(3): 196-199.

[10] Barndorff-nielesn O E. Normal inverse Gaussian distribution and stochastic volatility modeling[J]., 1997, 24(1): 1-13.

[11] Do M N, VETTERLI M. The Contourlet transform: an efficient directional multiresolution image representation[J]., 2005, 14(12): 2091-2106.

[12] Cunha A L, Zhou Jianping, Do M N. The nonsubsampled Contourlet transform: theory, design and application[J]., 2006, 15(10): 3089-3101.

[13] Guo K, Labate D. Optimally sparse multidimensional representations using shearlets[J]., 2007, 39(1): 298-318.

[14] 朱华生, 徐晨光. Shearlet变换域自适应图像去噪算法[J]. 激光与红外, 2012, 42(7): 811-814.

ZHU Hua-sheng, XU chen-guang. Adaptive image denoising algorithm based on Shearlet transform[J]., 2012, 42(7): 811-814.

[15] Yi S, Labate D, Easley G R, et al. A shearlet approach to edge analysis and detection[J]., 2009, 18(5): 929-941.

[16] Deng C, Wang S, Chen X. Remote sensing images fusion algorithm based on shearlet transform[C]//, 2009: 451-454.

[17] Miao Q G, Shi C, Xu P F, et al. A novel algorithm of image fusion using shearlets[J]., 2011, 284(6):1540-1547.

[18] 江平, 张强, 李静, 等. 基于NSST和自适应PCNN的图像融合算法[J]. 激光与红外, 2014, 44(1): 108-113.

JIANG Ping, ZHANG Qiang, LI Jing. Fusion algorithm for infrared and visible image based on NSST and adaptive PCNN[J], 2014, 44(1): 108-113.

[19] Chaudhury K N. Acceleration of the shiftable O(1) algorithm for bilateral filtering and non-local means[J]., 2013, 22(4):1291-1300.

[20] Mihcak M K, Kozintsev I, Ramchandran K. Low-complexity image denoising based on statistical modeling of wavelet coefcients[J].,1999, 6(12): 300-303.

[21] Luisier F, Blu T, Unser M. A new SURE approach to image denoising: interscale orthonormal wavelet thresholding[J]., 2007, 16(3): 593-606.

[22] Zhou W, Bovik A C, et al. Image quality assessment: from error visibility to structural similarity[J]., 2004, 13(4): 600-612.

A New Image Denoising Algorithm Based on Shift-invariant Shearlet Transform Domain

SHI Manhong1，LIU Wei2

(1.,,233100,; 2.,,230031,)

A novel image denoising algorithm based on bilateral filtering and the normal inverse Gaussian model in shift-invariant shearlet transform domain has been proposed. The shift-invariant shearlet transform (SIST) is utilized to decompose the noised image. The fast bilateral filtering algorithm is used to deal with the low frequency sub-band coefficients; normal inverse Gaussian model for the prior model is used to describe the distributions of the image high frequency coefficients, and corresponding threshold function is derived from the model using Bayesian maximum a posteriori probability estimation theory to get denoised image. Test on different types of images and the experimental results show that our algorithm not only has better visual quality but also has higher peak signal-to-noise ratio (PSNR) and mean structural similarity (MSSIM).

image denoising，shift-invariant shearlet transform，bilateral filtering，normal inverse Gaussian model，Bayesian estimation

TP391

A

1001-8891(2016)01-0033-08

2015-08-14；

2015-12-28.

石满红（1987-），女，助教，研究方向计算机辅助几何设计。

安徽省自然基金资助项目（1508085MC55、1508085QB41）。