基于辐射探测器阵列的单个γ源定位方法

赵　娟　　高正明（荆楚理工学院　电子信息工程学院　　荆门　448000）（宝鸡高新技术研究所　　宝鸡　703）



基于辐射探测器阵列的单个γ源定位方法

赵娟1高正明2
1（荆楚理工学院电子信息工程学院荆门448000）
2（宝鸡高新技术研究所宝鸡721013）

摘要采用探测器阵列并通过数据的自动处理实现辐射源的定位，是信息时代物联网工程对辐射信息监控的基本要求。为此，本文初步讨论了数学分析法、数学统计法和邻近探测器数据比较法三种定位方法，并采用MCNP5软件对通道内单个γ源的一维定位监控进行了数值仿真分析。结果表明，数学分析法和数学统计法的定位能力均优于工程上常用的邻近探测器数据比较法，前者需要的探测器数量少，但在多个探测器存在时误差随探测器组合而产生较大的变化。数学统计法需要多个探测器形成阵列，但定位精度很高，可用于大剂量或重要放射性部件的精确位置监控。

关键词辐射探测，探测器阵列，γ源，定位方法

国防预先研究项目基金（No.51331040501、No.42604060101）资助

第一作者：赵娟，女，1979年出生，2009年于华中科技大学获硕士学位，研究领域为物联网盲均衡技术、无损检测与监控技术

SupportedbyNationalDefensePre-researchProjects（No.51331040501，No.42604060101）

Firstauthor:ZHAOJuan，female，bornin1979，graduatedfromHuazhongUniversityofScienceandTechnologywithamaster’sdegreein2009，focusing ontheblindequalization，thenon-destructivetestingandmonitoringtechnologies

Locationmethodofasinglegammasourcebasedonthedetectorsarray

ZHAOJuan1GAOZhengming2
1（School of Electronics and Information Engineering，Jingchu University of Technology，Jingmen 448000，China）2（Baoji Research Institute of High Technology，Baoji 721013，China）

AbstractBackground:Locationofradioactivesourcesbasedonthedetectorsarrayandautomaticaldata processingarethebasicrequirementsofradiationdetectionandmonitoringsystemintheInternetofthingsprojects. Purpose:Thisstudyaimsforthelocationalgorithmsoftheradioactivematerials.Methods:Threemethods，i.e.，the mathematicalanalyticalmethod，themathematicalstatisticalmethodanddatacomparisonmethodofadjacent detectors，areinvestigated，andonedimensionalsimulationofasinglegammasourceinatunnelwasperformedwith MCNP5software.Results:Simulationresultsshowthatthemathematicalanalyticalmethodwasmoreaccuratethan thedatacomparisonmethodofadjacentdetectors，butthedetectionerrorsvariedwiththechoiceofthecoupleddatum ofthedetectorswhenmoredetectorswereapplied.Themathematicalstatisticalmethodrequiredmoredetectorsto formanarraytoachievethemostaccurateresult.Conclusion:Themathematicalstatisticalmethodcanbeusedinthe locationofimportantorlargedosecomponents.

KeywordsRadiationdetection，Detectorsarray，Gammasource，Locationalgorithm

随着信息时代的到来，物联网工程已经成为当前科技和社会发展的重点，是未来社会经济发展的支柱产业之一[1]。在物联网工程中，传感器数据的信息化、自动化处理是提高物联网应用层用户交互应用感度和准确性的基本要求。在核技术应用领域，辐射探测器是获知核辐射信息的基本探测手段，是放射性材料相关检测的基本工具。辐射探测器能够探测和获知放射性材料辐射信息的类型、强度、位置等信息[2-3]，可用于加速器辐射泄露的检测[4]，实验结果很好[5]。正常工况监控中，目前已有研究探测辐射粒子在流体中的运动轨迹反演位置信息的方法[6]，还可以根据辐射探测数据获得鼓泡塔内放射性材料的动态信息[7]。工程应用中辐射探测器多以阵列的形式部署，并具有最优的排列[8]。

在放射性材料储存库或国际核裁军进程中裁减后放射性部件的储存库管理过程中，对大剂量或重要部件的精确管理是十分必须的[9-10]。为此，本文研究了基于辐射探测器阵列反演γ辐射源的位置信息，实现重要放射性部件精确定位监控的方法。

1　定位方法

据核物理学相关理论，γ源空间附近的辐射场强度可采用通量描述，即无屏蔽空间任意一点的通量可表示为：

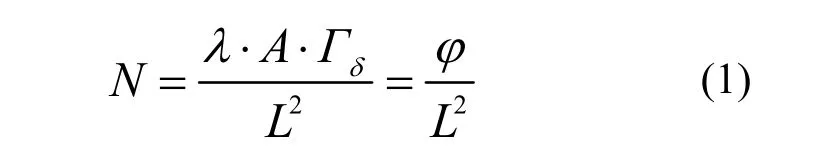
式中：N表示距离源为L的空间上任意一点的通量；A为γ源活度；Γδ为该点能量大于δ的γ射线造成的空气比释动能率；φ是与源的活度成正比的参量。

因此，理论上讲，若已知探测器阵列的计数率，则可以根据式（1）计算获得φ和位置信息。在数学上，求解此类问题有两种方法：数学解析法和统计法，而在工程上，多用邻近探测器比较法简单判定源的大致位置信息。

1.1数学解析法

由式（1）可知，若获得多个位置已知的探测器计数率，则可通过数学解析法对探测器位置和活度进行求解，所需探测器阵列的个数，与问题空间的维度有关。对于一维空间，探测器位置r和φ为未知量，则若获息两个分别位于r1、r2的探测器计数率，可通过联立方程式（2）进行数学解析运算。

式中：i＝1，2。二维平面问题中探测器位置（x，y）和三维空间问题中探测器位置（x，y，z）与φ为未知量，相应需要3和4个探测器组成阵列，才能进行数学解析。

1.2数学统计法

对探测器数据进行数学解析时，方程组为非线性方程组，一般采用高斯牛顿法（Gauss-Newton Algorithm，GNA）[11]、梯度下降法（GradientDescent Algorithm，GDA）[12]或Levenberg-Marquardt Algorithm（LMA）[13]进行求解。在数学求解过程中，不可避免地产生误差，尤其是探测器计数率的随机影响。为此，工程上常采用批量数据的统计分析法降低数据源的影响。

GNA、GDA或LMA均适用于方程组的数值解析和统计分析，其中LMA方法是GNA和GDA的组合，算法的鲁棒性更好，适用范围更广[14]。

对于一组数据（xi，yi），预拟合系数向量为p的非线性方程，LMA的基准准则是通过优化计算，寻找拟合优度[15]。

式中：ωi为权值；W为对角元素满足式（4）的矩阵参数，权值ωi和矩阵W存在如下关系：

LMA算法的基本过程是设定阈值ε，对比拟合优度比值，若ρi（h）＞ε，则p＝p＋h，反之不更新p继续搜索。拟合优度比值ρi（h）定义为：

增量h满足：

式中：J为拟合函数关于p的Jacobian矩阵。

1.3邻近探测器数据比较法

据式（1）可知，离源最近的探测器的计数率肯定最大，因此可判定该源的大致位置，但由于任意两探测器间计数率的差或比值均与其位置参数非线性性相关，因此无法精确估计探测器位置误差。该方法在工程上常用于找源，在一维模型中位置参数误差等于探测器阵列间距。

2　仿真实验分析与讨论

2.1仿真实验分析模型

考虑到辐射源一般使用场景，取上下左右均为墙壁的内部通道作为仿真实验设定场景，不考虑通道长度的影响，在通道上侧设置一系列间距100cm的澳大利亚堪培拉公司的Inspector1000NaI（Tl）探测器，在通道地面上放置一个60Co点源，各向同性。采用MCNP5程序开展MonteCarlo数值仿真分析，通道高280cm、宽260cm，点源和探测器中心均位于中轴面上。为便于建模，将空间倒置，即源位于顶侧，探测器位于地面上，仿真实验场景如图1所示。取某一探测器中心为原点，通道方向为Y方向，辐射源在Z轴上，建立笛卡尔坐标系，则中轴面为YOZ面，源位于（0，280，-150）处，探测器中心分布于Y＝0，100，200，…，其中NaI（Tl）探测器结构示意图如图2所示。

图1　模拟实验场景Fig.1　Scenario　of　simulation　model.

图2　NaI（Tl）探测器栅元组成示意图Fig.2　Structural　scheme　of　composited　cells　of　NaI（Tl）detector.

据粒子输运理论可知，探测器晶体栅元平均接收的粒子数即表征该点的γ通量，各探测器位置和仿真实验结果如表 1所示。

2.2数学解析法定位结果与分析

由数学解析法可知，探测器的计数率应满足：

式中：h＝280；x为源位置变量；y为源的活度参量；（ri，Ni）为探测器位置和计数率，则任意挑选一组探测器数据开展数学解析，采用MATLAB中的fsolve函数，并定义算法为LMA，误差为1×10-20，最大迭代次数为1×105，解析结果如表2所示。

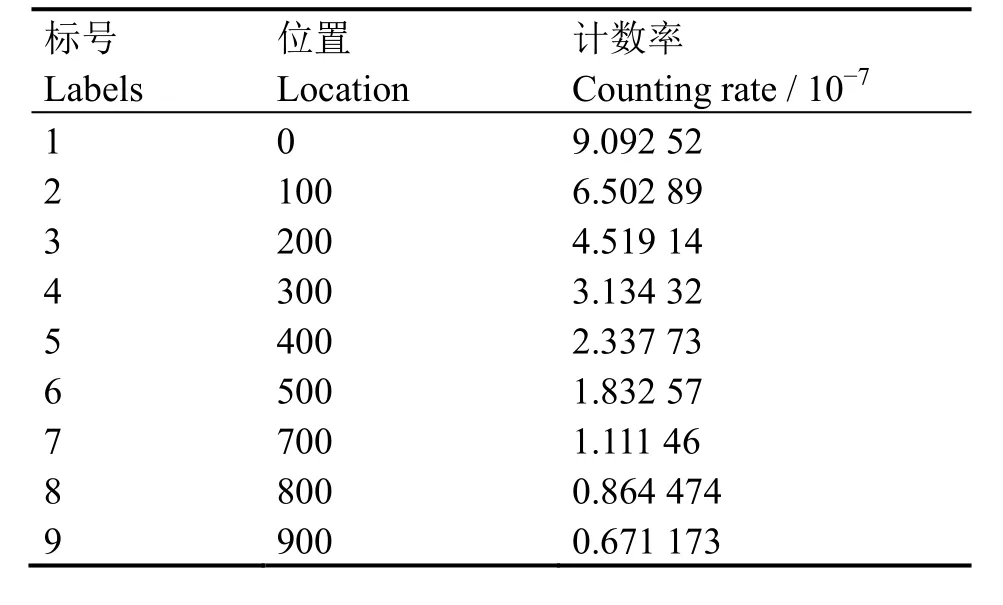
表1　Monte　Carlo数值仿真结果Table1　Monte　Carlo　simulation　results.

表2　基于数学解析法的定位结果Table　2　Analytical　results　of　the　location.

由表2可知，采用数学解析法进行定位分析时，随机选择的10组数据中，定位误差最大值为38%，最小值为1.5%，变化很大。此外，需要特别指出的是，γ探测器对天然本底辐射的响应较灵敏，实践上定位误差将进一步增加。

2.3数学统计法定位结果与分析

由于钴源辐射的粒子能量较高，离源较远的距离的探测器也能够获得信息，因此，应用数学统计分析时，将存在数据参与数量的对比问题。采用Origin9软件进行数据拟合分析，拟合选项为NonlinearCurveFit-PeakFunctions-InvsPoly，并根据式（7）在代码中定义初始约束“y0＝0;A1＝1;w＝560; A2＝0; A3＝0”，拟合许可误差1×10-20，最大迭代次数1×105得到的结果如表3所示。

由表3可知，在数据量较小时，数学统计法并不一定能够实现显著性回归，但探测器较多数据量较大时，定位精度很高。

表3　基于数学统计法的定位结果Table　3　Statistical　calculation　results　of　the　location.

3　分析与讨论

数值仿真实验结果表明，工程上常用的邻近探测器数据比较法由于只能提供粗糙的位置信息，不如数学解析法准确。但数学解析法的定位误差随探测器组合的选择不同而发生较大的变化。统计分析法具有较高的误差，但是需要足够数量的探测器形成阵列，以使非线性拟合显著性回归。

此外，三种方法之中，邻近探测器比较法操作最为简单，数学解析法由于选点问题影响太大，不具备操作性，而数学统计法数学原理清晰，可通过编制配套程序予以实现。在监控系统中应用时，邻近探测器比较法需要绘图显示或直接输出结果，但数据误差较大，而数学统计法可以绘图显示，还能够给出精确的数值解，且探测器阵列提供的数据越多，统计分析结果越准确。

在仿真实验中，采用的60Co源的γ射线穿透力强，探测器布局易于实现。而核电站、武器中使用的放射性材料的γ辐射强度也很强，根据本文研究可知也可以采用数学统计法进行定位分析。但其它一些弱γ源，如137Cs、75Se等，γ射线能量较低，穿透力弱，难以实现近10个探测器的阵列的布局。因此，本方法适用于具有较高γ射线能量的大剂量源的定位分析，可用于核裁军进程中裁减后放射性部件、核电站燃料部件等的精确定位监控与管理。

4　结语

本文讨论了三种γ源的定位方法，并基于MCNP5软件开展了MonteCarlo数值仿真实验，结果表明，工程上常用的邻近探测器数据比较法可以提供源的粗糙位置信息，但是数学解析法在一定程度上可以给出更准确的位置信息，存在的问题是误差随探测器组合的不同发生较大幅度的变化。而数学统计法可以提供更高精度的位置信息，该方法要求具有足够数量如大于9个的探测器形成阵列。

参考文献

1 MiorandiD，SicariS，DePellegriniF，et al.Internetof Things:vision，applicationsandresearchchallenges[J]. AdHocNetworks，2012，10（7）:1497-1516.DOI: 10.1016/j.adhoc.2012.02.016

2 GamageKAA，TaylorGC.Neutrongammafraction imaging:detection，locationandidentificationofneutron sources[J].NuclearInstrumentsandMethodsinPhysics ResearchSectionA:Accelerators，Spectrometers，DetectorsandAssociatedEquipment，2015，788:9-12. DOI:10.1016/j.nima.2015.03.072

3 ZhaoXJ，FuJJ，XuFR，et al.Irradiationdetectionof oilseedcropsbyelectronspinresonance[J].Nuclear ScienceandTechniques，2013，24（S1）:S010309.DOI: 10.13538/j.1001-8042/nst.24.S010309

4 JanataE.Determinationoflocationandintensityof radiationthroughdetectionofCherenkovemissionin opticalfibersPart1:methodandexperimental[J].Nuclear InstrumentsandMethodsinPhysicsResearchSectionA: Accelerators，Spectrometers，DetectorsandAssociated Equipment，2002，493（1-2）:1-7.DOI:10.1016/S0168-9002（02）01553-X

5 JanataE，KörferM，SchlarbH.Determinationoflocation andintensityofradiationthroughdetectionofCherenkov emissioninopticalfibersPart2:preliminaryresults obtainedatTTF[J].NuclearInstrumentsandMethodsin PhysicsResearchSectionA:Accelerators，Spectrometers，DetectorsandAssociatedEquipment，2004，523（3）: 256-261.DOI:10.1016/j.nima.2004.01.001

6 VieiraWS，LuísEduardoBB，BrazD.Analternative methodfortrackingaradioactiveparticleinsideafluid[J]. AppliedRadiationandIsotopes，2014，85:139-146.DOI: 10.1016/j.apradiso.2013.12.006

7 SaliernoGL，MaestriM，PiovanoS，et al.Discreteaxial motionofaradioactivetracerreconstructedfromthe responseofaxiallyaligneddetectors:applicationtothe analysisofabubblecolumndynamics[J].Chemical EngineeringScience，2013，100:402-412.DOI: 10.1016/j.ces.2013.03.029

8 OlivierDubé，DavidDubé，JamalChaouki，et al. Optimizationofdetectorpositioningintheradioactive particletrackingtechnique[J].AppliedRadiationand Isotopes，2014，89:109-124.DOI:10.1016/j.apradiso. 2014.02.019

9 OfficeofNonproliferationResearchandEngineering. TechnologyR＆Dforarmscontrol[M/OL].2001

10 DaiJR，MaP，CuiWJ.Evaluationofdosimetryeffectof lackofside-scattervolumeonlargefieldmeasurements withaMapCheckdetectorarray[J].NuclearScienceand Techniques，2009，20（5）:292-296.DOI:10.13538/j.1001-8042/nst.20.292-296

11 ArgyrosIK，GeorgeS.Expandingtheapplicabilityofa modifiedGauss-Newtonmethodforsolvingnonlinear ill-posedproblems[J].AppliedMathematicsand Computation，2013，219（21）:10518-10526.DOI: 10.1016/j.amc.2013.04.026

12 IvieSJr.Numericaloptimizationforthecalculusof variationsbygradientsonnon-HilbertSobolevspaces usingconjugategradientsandnormalizeddifferential equationsofsteepestdescent[J].NonlinearAnalysis: Theory，Methods＆Applications，2009，71（12）: e665-e671.DOI:10.1016/j.na.2008.11.065

13 KeyvanA，FaramarzR.Amodifiedtwosteps Levenberg-Marquardtmethodfornonlinearequations[J]. JournalofComputationalandAppliedMathematics，2015，288:341-350.DOI:10.1016/j.cam.2015.04.040

14 Herrera-SolazV，SeguradoJ，LlorcaJ.Ontherobustness ofaninverseoptimizationapproachbasedonthe Levenberg-Marquardtmethodforthemechanicalbehavior ofpolycrystals[J].EuropeanJournalofMechanicsA: Solids，2015，53:220-228.DOI:10.1016/ j.euromechsol.2015.05.005

15 StefanF，KowalskyMB.Atruncated Levenberg-Marquardtalgorithmforthecalibrationof highlyparameterizednonlinearmodels[J].Computers＆Geosciences，2011，37（6）:731-738.DOI:10.1016/j. cageo.2010.11.005

收稿日期：2015-10-12，修回日期：2015-12-16

DOI:10.11889/j.0253-3219.2016.hjs.39.010402

中图分类号TL38＋4，TL929