咸水入侵探测中电阻率法测量数值模拟研究

佟　雪， 孟庆生，b， 杨　俊， 韩　凯， 肖志广

(中国海洋大学　a.环境科学与工程学院，

b.海洋环境与生态教育部重点实验室， 青岛　266100)



咸水入侵探测中电阻率法测量数值模拟研究

佟雪a， 孟庆生a，b， 杨俊a， 韩凯a， 肖志广a

(中国海洋大学a.环境科学与工程学院，

b.海洋环境与生态教育部重点实验室， 青岛266100)

摘要：近年来海(咸)水入侵已成为影响居民生活、制约工农业发展的重大问题，确定咸淡水界面是治理海(咸)水入侵的重要前提。根据咸淡水的电性差异，针对两种典型的咸水入侵地电模型进行正、反演计算，并研究了不同因素对电阻率法测量咸淡水界面的影响。结果表明：①电阻率法数值模拟可以较好地反映咸淡水界面的位置及形态；②咸化程度和现场实测范围内的粘土层电阻率变化对咸淡水界面的测量无明显影响；③测量极距主要影响反演剖面的分辨率，极距越小，分辨率越高。

关键词：咸水入侵； 电阻率； 正演模拟； 反演； 影响因素

0引言

随着人类对水资源需求量的增加，对地下水的开采量也在不断增加，但由于缺乏对地下水资源分布及储量的科学认识，很多滨海地区出现因超量开采地下水而引起的海水入侵问题，进而对当地的生产、生活造成了严重威胁。因此，为保障当地居民的生活用水和工农业用水安全，保护水源地的持续开发、利用，必须准确地查明咸水入侵程度和范围，并提出合理的防治对策[1]。

电阻率是物质的基本特性之一[2]，近年来以电阻率测试为代表的地球物理探测方法被广泛应用在地下水调查研究领域，研究显示，将电阻率法应用于水中重金属污染物监测[3]、水库坝址工程地质条件调查[4]，垃圾填埋场渗漏检测[5]等方面，均取得了良好效果。根据咸水与淡水之间的电性差异，利用电阻率剖面法可以界定咸、淡水界面的位置及形态，从而实现对咸、淡水界面运移规律的分析和监测[6-7]。虽然目前国、内外许多研究者进行了一些相关的实际应用，但是其应用效果褒贬不一，对利用电阻率法探测过程中的一些影响因素和采集方式缺乏充分的理论认知，从而影响了该方法的广泛应用。

这里通过有限差分法( Finite-Difference Time Domain，FDTD)对咸水入侵区电阻率的分布情况进行数值模拟计算，研究电阻率法对不同形态咸、淡水界面的监测效果，以及不同影响因素对电阻率法测量咸淡水界面的影响，以期为分析实测数据、圈定入侵范围、提出治理对策提供理论依据。

1基本理论

1.1二维电阻率法正演

由电阻率空间分布求取电场分布的计算过程称为正演模拟，正演模拟的解是唯一的。电法正演模拟方法大致分为解析法、物理模拟法和数值模拟法三类[8]。对于复杂电性结构下的电阻率正演模拟计算，数值模拟法优于解析法和物理模拟法[9-10]。正演数值模拟主要有α中心法、积分方程法、边界元法、有限差分法和有限单元法等，其中有限差分法和有限元法使用最为广泛。有限元法适用于模拟物性参数复杂分布的区域和地形起伏的条件，但运算量大，计算效率相对较低[11-12]；与有限元法相比，有限差分法程序简单，不涉及计算耗时的偏导数运算，易于在计算机上实现[13]。作者正演计算采用有限差分法，基本步骤如下[14]：

1)对研究区域作网格剖分,用有限个网格节点代替连续空间,以这些节点上的电场值表示电场的空间分布。

2)将微分方程离散化，组建逼近微分方程边值问题的差分方程,得到以各节点的电场值为未知量的线性方程组。

3)求解线性方程组，得到各节点的电场值，即问题的数值解。

1.2二维电阻率反演

电阻率法反演计算建立在正演的基础上，其目的为根据地面上的观测信号求取地球内部相应的物理性质[15]。反演计算采用M．H．Loke的RES2DINV软件，其二维反演采用平滑约束最小二乘法，此算法建立在方程(1)的基础上。

(JTJ+μF)d=JTg

(1)

2数值模拟

2.1楔形界面模型

针对楔形咸、淡水界面构建地电模型，如图1所示。第一层为粘土层(ρ1=50 Ω·m)，厚度为2 m；第二层为砂和砂砾石层，厚度为4 m，地下水主要分布于第二层中，从左至右依次为咸水入侵区(ρ2=5 Ω·m)，咸淡水过渡带(ρ3=12 Ω·m)和淡水区(ρ4=30 Ω·m)；第三层为隔水层(ρ5=100 Ω·m)，厚度为2 m。图中白色实线所夹区域为咸淡水过渡带，电极位于空气与粘土层的交界面上。

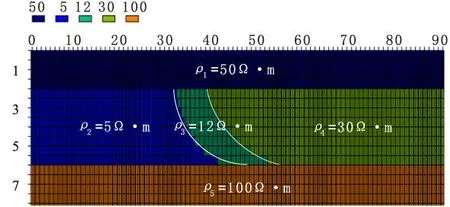
图1　楔形界面地电模型图Fig．1　Geoelectric model diagram of wedge interface

测量装置为温纳装置，该装置是对称四极装置中的一种，具有良好的抗噪声性能，在电法探测中应用广泛[3]。沿测线方向电极个数为91个，电极极距为1.0 m。通过有限差分法，将理想地电模型划分为矩形网格，相邻电极之间是4个节点。图2(a)为楔形界面模型正演计算结果，利用最小二乘法进行反演计算，并使用Surfer软件进行处理，结果如图2(b)所示。

由图2(b)可以看出，粘土层的电阻率值由浅至深逐渐减小，但与实际模型基本吻合；淡水区的电阻率接近于模型的实际情况。

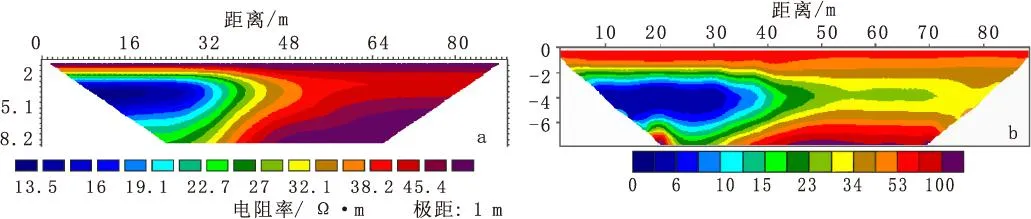
图2　楔形界面模型正反演计算结果((Wenner-α装置))Fig．2　The forward modeling and inversion calculation results of wedge interface model(a)正演结果;(b)反演结果

由综合分析数值模型和反演剖面可知，咸水入侵区的范围与模型基本一致；咸水区轮廓清晰，边界收敛性较好，但与实际模型中咸水区和隔水层之间的突变界面不同，该界面在反演结果中显现为一个渐变的趋势分界面。其原因在于电阻率法观测中获得的电阻率是地下各种地质体电性影响的综合反映，使得结果中不同电性区分界面处的电阻率呈现出一个平滑的变化过程。此外我们还发现，模型反演结果并没有很好地展示出咸、淡水接触带的真实产状特征，究其原因在于：① 咸水入侵的楔状模型类似于梯形低阻体，由于其与周围地层的电阻率有很大差异，当电流在地下传播时，电场电流线受低阻异常体的吸引，形成局部聚集，改变了电阻率界面处的电场分布特征，同时也改变了分界面附近区域的电场分布规律；② 由电阻率法测量原理可知，随着探测深度的增加，测量数据点数相应的减少，探测精度也会因此而降低，直流电阻率法勘探的分辨能力随深度的增加而逐渐变差。由于上述原因，再加上平滑约束算法的自身缺陷，便造成了反演结果中浅部接触带与模型相吻合，深部接触带产状与模型有所不同。

2.2突变界面模型

在开展数值模拟研究之前，作者通过室内试验和调查资料获知研究区的咸水入侵界面呈现突变趋势，针对这一情况也构建了突变界面地电模型，如图3所示。模型基本参数如下：沿测线方向排列91个电极，电极极距为1 m，测量装置为温纳装置，水平地形。第一层为粘土层(ρ1=50 Ω·m)，粘土层厚度为2 m；第二层为砂和砂砾石层，厚度为4 m，地下水主要分布于第二层中，从左至右依次为咸水入侵区(ρ2=5 Ω·m)和淡水区(ρ3=30 Ω·m)，咸水区与淡水区之间不存在过渡带，呈现突变趋势；第三层为隔水层(ρ4=100 Ω·m)，厚度为2 m。采用地面测量方式，图4中白色实线表示咸淡水突变界面。

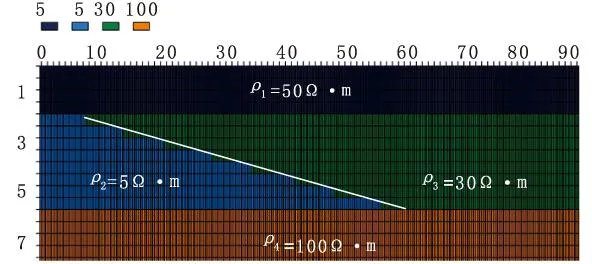
图3　突变界面地电模型图Fig．3　Geoelectric model diagram of abrupt interface

由图4(b)可知，较楔形过渡带的咸水入侵模型而言，突变模型经计算得到的反演断面图更加接近于模型的实际情况。咸水区的上表面倾斜，与模型相吻合，咸水区范围与模型保持一致，通过平滑约束算法得到的反演结果显示在咸水区与隔水层之间有一个过渡的边界，基本对应模型中的突变边界。总体上，咸水区的位置和范围都与模型基本一致。咸淡水界面收敛性较好，能够清晰地反映出实际问题，粘土层和淡水区的电阻率值均与实际相吻合。与楔形界面模型类似，突变界面模型反演结果中也不能很好地反映出入侵界面的真实产状，这在今后的实际应用中应引起关注。

3测量效果的影响因素分析

在使用电阻率法确定咸淡水分界面时，不同的外界因素会对最终的测量结果产生不同的影响。以突变界面模型为研究对象，通过正、反演数值模拟法来分析在咸水入侵情况下，咸化程度、粘土层电阻率值以及单位电极距等因素对电阻率法测量咸淡水界面的影响。

3.1咸化程度对测量咸淡水界面的影响

模型构建同上，针对咸水入侵区不同咸化程度进行数值模拟，咸水区电阻率值ρ2分别取5 Ω·m、10 Ω·m和15 Ω·m。电极位于粘土层表面，正、反演计算结果如图5和图6所示。

图6为不同咸化程度下，咸水入侵突变模型的二维反演电阻率断面图，咸水区的上表面倾斜，与模型相吻合。当ρ2=10 Ω·m时，淡水区的电阻率范围接近于模型的30 Ω·m；隔水层的电阻率接近于模型的100 Ω·m。咸水区的范围与模型基本吻合。

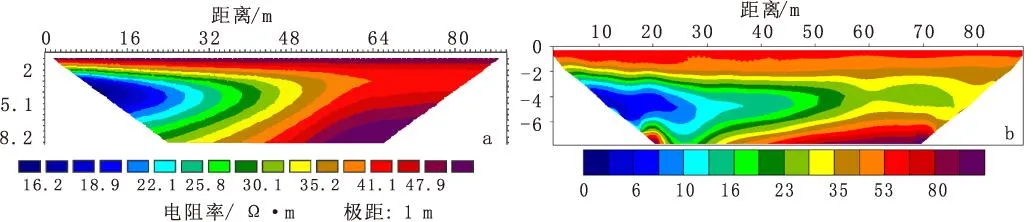
图4　突变界面模型正反演计算结果(Wenner-α 装置)Fig．4　The forward modeling and inversion calculation results of abrupt interface model(a)咸水入侵突变界面模型正演计算结果；(b)反演计算结果

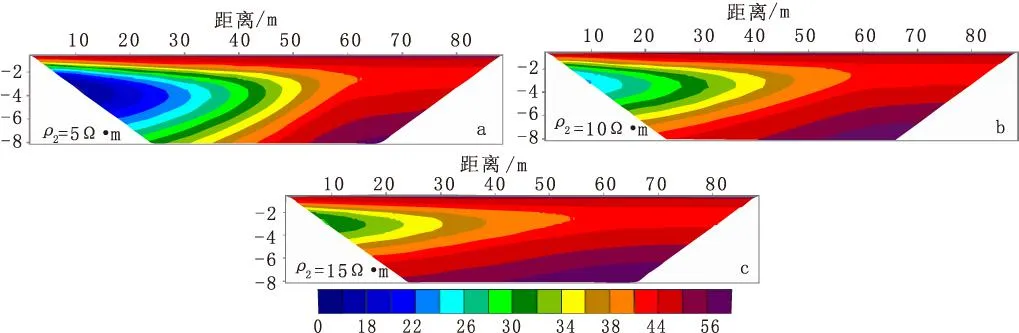
图5　模型不同咸化程度正演计算结果(Wenner-α 装置)Fig．5　The forward modeling results of models with different salinization degrees(a) ρ2=5 Ω·m;(b) ρ2=10 Ω·m;(c) ρ2=15 Ω·m

图6　模型不同咸化程度反演计算结果(Wenner-α 装置)Fig．6　The inversion modeling results of models with different salinization degrees (a) ρ2=5 Ω·m;(b) ρ2=10 Ω·m;(c) ρ2=15 Ω·m

比较图6中(a)、(b)、(c)可知，随着咸化程度的增大，各区域的电阻率值无明显变化，在水平和竖直两个方向上，咸水入侵区的范围都有相应程度的减小。当ρ2=5 Ω·m时，咸水区的水平宽度更加接近于模型实际情况；当ρ2= 15 Ω·m时，咸水区的垂直深度与模型相近。当咸水区电阻率大于10 Ω·m时，咸水区范围变化较为明显，但依旧轮廓清晰，边界收敛性良好。

综上所述，咸化程度即咸水区电阻率值对各区域电阻率的测量无明显影响，而对反演结果中咸水区的范围存在一定程度的影响。由于平滑约束算法的自身缺陷，反演计算结果中在含水层底部与隔水层顶部之间的突变边界变得模糊，咸化程度越大，二者之间的过渡趋势越明显；当咸水区电阻率为10 Ω·m时，咸水区的位置和范围均最接近于模型实际。

3.2粘土层电阻率对测量咸淡水界面的影响

基于咸水入侵模型结构，咸水区的电阻率值为10 Ω·m，根据不同季节开展电阻率法现场实测得到的粘土层电阻率变化范围，分别对不同粘土层电阻率值(ρ1=50 Ω·m、80 Ω·m、120 Ω·m)进行建模。淡水区和隔水层的电阻率值，以及模型各部分的形状、尺寸、空间分布情况均保持不变。数值计算过程同上节，正演计算结果如图7所示。

在Surfer软件中对反演结果进行绘制，得到的二维反演电阻率断面见图8。当粘土层的电阻率为80 Ω·m时，反演结果中粘土层的电阻率变化范围接近于模型实际；淡水区的电阻率值变化范围与模型基本一致。当ρ1=120 Ω·m时，粘土层的电阻率与模型实际相吻合，反演结果基本上可以准确的反映咸水入侵的程度和范围。

比较图8中(a)、(b)、(c)可知，随着粘土层电阻率的增大，反演计算结果中咸水区的范围有极小程度的增加，这对咸水区的测量不足以构成影响；在垂直方向上，咸水区的位置和范围无变化，边界收敛性较好；各区域的电阻率值也无明显变化。

由电阻率法原理可知，浅表层的电阻率变化会对探测结果造成一定程度的影响。当表层电阻率变化较大时，探测结果会出现明显差异；然而，粘土层电阻率仅在实测范围内变化，此时探测结果无明显差异。综上所述，通过改变粘土层的电阻率值进行数值模拟可以发现，粘土层电阻率值在现场实测范围内的变化对咸淡水界面的测量基本无影响。

3.3电极极距对测量咸淡水界面的影响

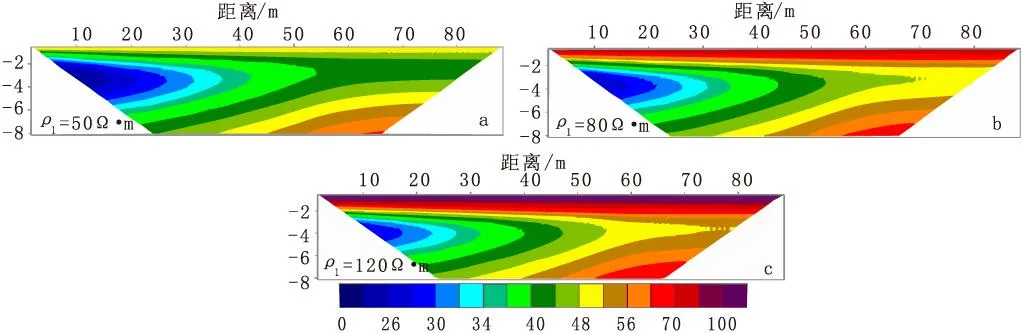
图7　模型不同电阻率粘土层正演计算结果(Wenner-α 装置)Fig．7　The forward modeling results of models with different resistivity-clay layer (a) ρ1 =50 Ω·m;(b) ρ1 =80 Ω·m;(c) ρ1 =120 Ω·m

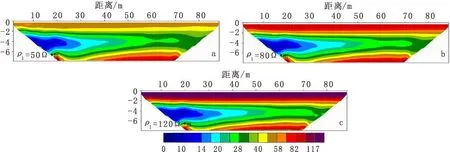
图8　模型不同电阻率粘土层反演计算结果(Wenner-α 装置)Fig．8　The inversion modeling results of models with different resistivity-clay layer(a) ρ1 =50 Ω·m;(b) ρ1 =80 Ω·m;(c) ρ1 =120 Ω·m

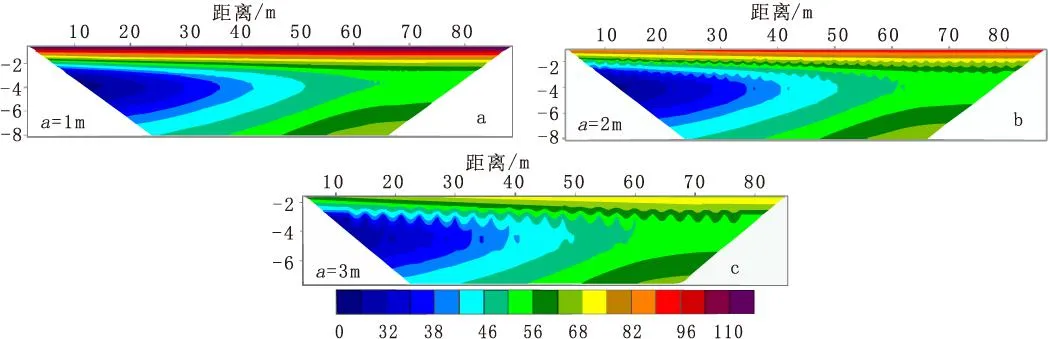
图9　模型不同电极极距正演计算结果(Wenner-α 装置)Fig．9　The forward modeling results of models with different polar distance(a)1 m;(b)2 m;(c)3 m

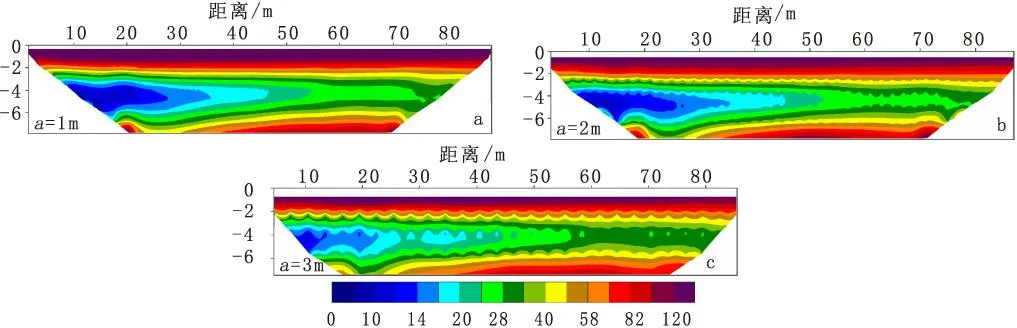
图10　模型不同电极极距反演计算结果(Wenner-α 装置)Fig．10　The inversion modeling results of models with different polar distance(a)1 m;(b)2 m;(c)3 m

在以上研究的基础上建立地电模型，咸水入侵区电阻率值为10 Ω·m，粘土层电阻率值为120 Ω·m，模型其他各部分电阻率值及空间分布情况保持不变。测量装置为温纳装置，测线长度保持90 m不变，电极极距分别为1.0 m、2.0 m和3.0 m，对应的电极个数为91个、46个和31个，无地形数据。经数值计算后，正演计算结果如图9所示。

不同测量极距下，模型反演计算结果如图10所示。当单位电极距a=2.0 m和3.0 m时，反演断面的分辨率明显降低，而计算结果中粘土层、淡水区和隔水层的电阻率变化范围均与模型相吻合，无明显变化。由此可知，测量极距对模型各区域电阻率的测量无明显影响。

比较图10中(a)、(b)、(c)可知：随着测量极距的增大，电阻率轮廓线的波动幅度增大，电阻率剖面的分辨率降低；咸水区的范围在水平方向上有一定程度的减小；各区域的电阻率值无明显变化。

综上所述，测量极距主要影响反演剖面的分辨率，采用的电极极距越大，反演剖面的分辨率越低，因此，在时间、天气等外界因素允许的情况下，为保证数据质量，应选择较小的电极极距进行现场测量。

4结论

以咸水入侵为背景，针对电阻率的分布情况采用FDTD方法建立咸水入侵地电模型，经正、反演计算得到了对应的电阻率剖面，并以突变模型为例，通过数值模拟法分析了咸化程度、粘土层电阻率以及测量极距等因素，对电阻率法测量咸淡水界面的影响，主要结论如下：

1)数值模拟法能够成功获得含水介质中咸、淡水界面的位置与形态，电阻率断面可以反映出咸水入侵的程度和范围。

2)咸化程度和现场实测范围内粘土层电阻率的变化，对模型各区域电阻率的测量均无明显影响。

3)测量极距主要影响电阻率剖面的分辨率，极距越大，反演断面的分辨率越低。

4)为准确获得入侵界面的产状特征，应进一步研究有效的数据反演手段，提高反演精度。

参考文献：

[1]边余佳，李德彬，杨小芳. 我国海水入侵及防治措施[J]. 科技信息，2009，21：435.

BIAN Y J，LI D S，YANG X F. Seawater intrusion and counter measures in China[J]. Science and Technology Information，2009，21：435.(In Chinese)

[2]罗维斌，李庆春. 电阻率法监测地下地质变化的数值模拟[J]. 物探与化探，2011，35 (4) :557-561.

LUO W B，LI Q C. Numerical modeling of geoelectrical time-lapse monitoring subsurface[J]. Geophysical and Geochemical Exploration，2011，35 (4) :557-561. (In Chinese)

[3]王玉玲，能昌信，王彦文，等. 重金属污染场地电阻率法探测数值模拟及应用研究[J]. 环境科学，2013(05)：1908-1914.

WANG Y L，NENG C X，WANG Y W，et al. Numerical simulation and application of electrical resistivity survey in heavy metal contaminated sites[J]. Environmental Science，2013(05)：1908-1914. (In Chinese)

[4]葛双成，李小平，邵长云，等. 地震折射和电阻率法在水库坝址勘察中的应用[J]. 地球物理学进展，2008(04)：1299-1303.

GE S C，LI X P，SHAO C Y，et al. Application of seismic refraction and resistivity for exploration of reservoir dam site[J]. Progress in Geophysics，2008(04)：1299-1303. (In Chinese)

[5]刘国辉，徐晶，王猛，等. 高密度电阻率法在垃圾填埋场渗漏检测中的应用[J]. 物探与化探，2011(05)：680-683+691.

LIU G H，XU J，WANG M，et al. The application of high-density resistivity method to landfill leakage detection[J]. Geophysical and Geochemical Exploration，2011(05)：680-683+691. (In Chinese)

[6]ADEPELUMI A A, AKO B D, AJAYI T R, et al. Delineation of saltwater intrusion into the freshwater aquifer of Lekki Peninsula, Lagos, Nigeria[J]. Environmental Geology, 2009(56): 927-933.

[7]MANSOUR A, AL-GARNI·HESHAM M, EL-KALIOUBY. Delineation of saline groun-dwater and sea water intrusion zones using transient electromagnetic (TEM) method, Wadi Thuwal area, Saudi Arabia[J]. Arabian Journal of Geosciences, 2011, 4(3): 655-668.

[8]张胜业，潘玉玲. 应用地球物理学原理[M]. 北京：中国地质大学出版社，2004．

ZHANG S Y，PAN Y L. The principle of applied geophysics[M]. Beijing：University of Geosciences Press，2004. (In Chinese)

[9]吴曲波，张志勇，柯丹，等. 点源二维直流电阻率法正演模拟[J]. 工程地质物理学报，2014，11(1) :44-49.

WU Q B，ZHANG Z Y，KE D，et al. The forward modeling of 2D resistivity for point-source electric field[J]. Chinese Journal of Engineering Geophysics，2014，11(1) :44-49. (In Chinese)

[10]徐世浙，张桂青. 地球物理中的有限单元法[M]. 北京：科学出版社，1994.

XU S Z，ZHANG G Q. The finite element method in geophysics [M]. Beijing：Science Press，1994. (In Chinese)

[11]阮百尧，熊彬. 电导率连续变化的三维电阻率测深有限元模拟[J]. 地球物理学报，2002，45 (1) :131-138.

RUAN B Y，XIONG B. A finite element modeling of three-dimensional resistivity sounding with continuous conductivity[J]. Chinese Journal of Geophysics，2002，45 (1) :131-138. (In Chinese)

[12]JACKSON P D, EARL S J, REECE G J. 3D resistivity inversion using 2D measurements of the electric field [J]. Geophysical Prospecting,2001,49: 26-39.

[13]DEY A ,MORRISON H F. Resistivity modeling for arbitary shaped three- dimensional structures[J]. Geophysics , 1979,44 (4) :753-780.

[14]施庆国. 高密度电阻率法二维和三维有限差分正演计算[D]. 长春：吉林大学，2012.

SHI Q G. 2D,3D finite-difference forward calculations of high-density resistivity method[D]. changchun：Jilin University，2012. (In Chinese)

[15]余金煌，陶月赞. 高密度电法探测水下抛石体正反演模拟研究[J]. 合肥工业大学学报:自然科学版，2014，37(3)：333-337.

YU J H，TAO Y Z. Research on high density resistivity method’s forward and inversion simulation of underwater enrockment[J]. Journal of Hefei University of Technology，2014，37(3)：333-337. (In Chinese)

Numerical simulation of resistivity mothed in saltwater intrusion prospecting

TONG Xuea， MENG Qing-shenga,b， YANG Juna， HAN Kaia， XIAO Zhi-guanga

(a. College of Environmental Science and Engineering, Ocean University of China, Qingdao266100, China;b. Key Laboratory of Marine Environment Science and Ecology, Ministry of Education, Qingdao266100, China)

Abstract:In recent years, the sea water intrusion has become a serious problem for the residents living and restriction of industry and agriculture developing. Determining the salt-fresh water interface is the important premise of sea water intrusion management. According to the electric difference between salt water and fresh water, 2D resistivity forward and inversion of two typical saltwater intrusion geo-electric models were performed, and the effects of different factors on the resistivity measurement of salt-fresh water interface were studied. The results show that the numerical simulation of resistivity method can well reflect the position and the shape of salt fresh-water interface. There is no obvious effect of salinization degree and the change of clay layer resistivity within the measured range on the measurement of salt-fresh water interface. Measuring electrode spacing mainly affects the resolution of inversion profile, the resolution of resistivity profile increases with the decrease of electrode spacing.

Key words:saltwater intrusion; resistivity; forward modeling; inversion; influence factor

中图分类号：P 631.3

文献标志码：A

DOI：10.3969/j.issn.1001-1749.2016.01.01

文章编号：1001-1749(2016)01-0001-07

作者简介：佟雪(1991-)，女，硕士，主要从事海水入侵监测技术研究工作，E-mail:735069764@qq.com。

基金项目:水利部公益性行业科研专项(201301090)

收稿日期：2015-01-26改回日期：2015-02-21