减负增效背景下课堂教学的数学化提炼

李景祥

【摘要】 新课程理念中提到关注学生学习的过程，通过创设学习情境、开发实践环节和拓宽学习渠道，帮助学生在学习过程中体验、感悟、建构并丰富学习经验，实现知识传承、能力发展、积极情感形成的统一。而实际数学知识在许多人的心目中，是枯燥无味的，教学过程就是填鸭式的传授，如何转变枯燥无味为生动有趣的教学过程呢？我们应深刻地认识到在教学改革中提出的减负增效目的是为了提高教师的课堂教学水平和质量，驾驭好课堂教学艺术的改革。于是现在很多场合的公开课上，教师都积极创设问题情景，以显示数学与生活的密切关系，并能用数学解决实际生活问题；然情景教学归情景，与数学思想转化之间是两张皮，现引用几堂课中的情景教学入手，浅谈如何实现情景的数学化提炼。

【关键词】 减负增效 课堂教学

【中图分类号】 G632.4 【文献标识码】 A 【文章编号】 1992-7711（2016）02-025-010

1.现实情景的数学化

“二分法”这堂课由于通过判断函数零点的存在性：闭区间上的连续函数”，一教师创设“商品猜价格”游戏，通过让学生猜商品价格后老师提示“高了”还是“低了”，说高了往低猜，说低了往高猜，不断逼近商品的正确价格，由此引入“二分法”概念。而后，以一个具体方程的求近视解为例，经历求解的过程，总结出“二分法”求方程近视解的一般步骤，整堂课教学过程紧凑，知识的生成也自然，唯独在“竞猜价格”游戏情景中只见“二分法”中的取中点，学生未见到“连续函数”，未见到“闭合间端点的函数取异号”等等，因此教学过程只关注“情景的引入”，而未关注“数学思想的转化”；下面是一个提炼过程。

（1）设商品的价格为m元（定量，学生不知道），范围在a与b之间，即，学生猜价格为x元，两者间的差距组成一个连续函数，定义域为[a，b]，f（a）<0，f（b）>0，若第一次即猜对即，否则继续下一步。

（2）学生取元，若猜高了，说明，则价格在区间[a，]之间再取中点；反之，若猜低了，说明，则价格在区间[]之间再取中点。

⑶以此类推，区间长度越来越小，学生猜的价格也越来越逼近真实价格，达到一定范围，而所猜的价格就是方程解的近视值，猜对时就是方程的解。

猜价格游戏从学生的认识抽象到数学模型的认知过程，让学生也经历了一个从具体现实问题到抽象数学思想的“数学化”提炼过程。

2.公式推导过程数学思想提炼

在讲授“两角和与差的余弦（第一课）”这节课，新的概念引入时，教师经常有意创设便于学生观察、分析、思考的情景，以便与所学知识与学生原来认知发生矛盾，制造悬念，激发他们的数学求知欲。因此教师在公开课时，设计了如下问题引入公式：

我们知道可写成，那么是否成立？经验证不成立，那么进一步设问，能否用的三角函数表示呢？一般式如何用的三角函数表示？至此，有的教师直接给学生用的推导公式进行检验，就教学方法来说，用特殊值去检验一个命题的真假，不失为一种好的办法，但是作为数学思想的讲授过程显然不符合思维的一般规律。

在引导学生推导公式时，教师有必要提出这么几个问题：

（1）为什么要在直角坐标系中通过单位圆推导？

（2）如何构造角？

（3）结合图像，运用向量方法推导公式的必备什么条件？

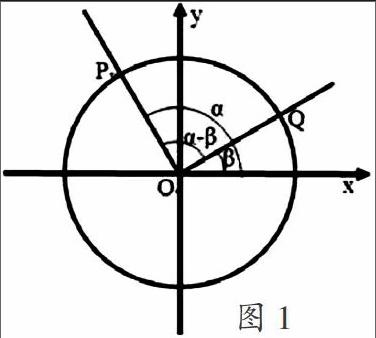
如果没有弄清楚这些问题，引导学生推导公式就会显得牵强，勉为其难；因此，应该这么考虑：在直角坐标系中研究三角函数是一种基本的数学研究，体现数形结合的思想；同时，建立与的三角函数关系，就是要寻找等量关系，如图1，在单位圆中构造，有，∠POQ=α-β，单位圆结合向量数量积的概念：

根据向量数量积的坐标运算：

即得出两角差余弦公式的推导过程。

“学起于思，思起于疑”，创设问题情境，引发学生合理的认知冲突，激发学生的认知内驱力；两角差的余弦公式推导是本节的重点，也是难点，尤其是引导学生通过主动参与，独立探究，自己得出结果更是难点。

3.问题情境创设

在《不等关系与不等式》中有这么一道题目：已知a，b，m均为正数，又b>a，证明，一般教师在上课时，直接利用作差法，给出证明过程，然而这个题目可以很好地创设情境激发学生数学思维。

引用“糖水问题”，即b克糖水中有a克糖（b>a>0），若再加入m克的糖，则糖水更甜了，这说明了什么？需要补充溶液、溶剂以及溶度的相关知识，糖水就是溶液b，含有糖a，即原先溶度为%，而后加入m克，此时溶度变为%，为什么变甜呢？溶度增加了！接下来师生可利用比较大小的方法，一起进行证明；像这类以实际问题为背景，可以使学生联系实际生活，更能提高课上的兴奋点。

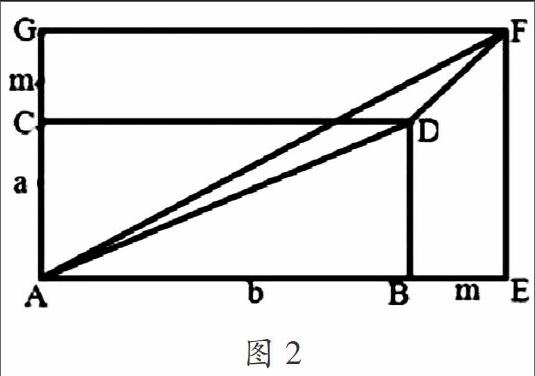
当然，对于知识的升华，可以引入“斜率法”，对于知识的迁移与整合，起到很好地效果：

如图2，画出矩形ABCD，长宽分别为b、a，然后将这个矩形长宽都延长m，得到大矩形AEFG，AD的斜率为，AF的斜率为，通过图形很容易看出，∠FAE<∠DAB，根据正切函数的单调性，因此即证之。

总之，减轻学生学习负担，应该从优化课堂教学的手段和方法入手，只要教师努力提高自己的自身业务素质，挖掘学生的最大潜力，充分发挥学生的学习主动性，在减负不减质的前提下，教师对已有的生活经验和数学的实际，转化“以教材为本”的旧观念，灵活处理教材，根据实际需要对原材料进行优化组合。而创设情境应注意从学生已有的生活经验合知识背景出发，让学生感觉到所面临的情境是熟悉的，使学生在轻松的氛围中，积极主动地参与学习，只有这样才能激发学生学习的兴趣与动机，加深学生对“身边处处有数学”的体会。