含测量时滞的离散时间随机系统的最优控制器设计

张鹏飞,张　志,刘欣涛

(青岛科技大学 自动化与电子工程学院,山东 青岛　 266042)



含测量时滞的离散时间随机系统的最优控制器设计

张鹏飞,张志,刘欣涛

(青岛科技大学 自动化与电子工程学院,山东 青岛 266042)

摘要针对网络诱发的时滞系统的状态估计和最优问题,研究离散时间情况下含有测量时滞的网络控制系统在随机白噪声状态下的最优控制问题。提出一种基于离散时间时滞系统的状态最优估计方法,并完成最优状态估计器的设计。构建一个隐含测量时滞的系统,然后利用无时滞转换方法,将含测量时滞的网络控制系统转换为无时滞系统,再采用卡尔曼滤波的方法对系统状态进行估计,得出最优估计方程。实现了针对含有测量时滞的网络控制系统的状态估计,完成最优控制器设计。仿真示例系统的状态响应验证了该方法的可行性和有效性。

关键词网络控制系统;测量时滞;卡尔曼滤波;状态估计;最优控制

计算机网络技术和控制理论相结合的研究领域成为目前控制界的一个研究热点。利用网络进行信息传输和控制,一方面为远程控制、系统管控一体化、系统工程带来信息的便捷,另一方面网络的数据传输特性也极大地影响了系统的性能。网络诱导时滞[1]、网络传输导致的系统的随机特性等,对基于通信网络的控制系统的信息采集、信息处理、控制器的设计等技术提出了新的挑战。

由网络传输而导致的网络化时滞系统,总是存在各种不确定性和随机性。对于随机系统状态反馈控制器的设计不得不考虑状态的重构和估计。考虑噪声环境下的状态估计和状态反馈将是更加符合实际的思路。卡尔曼滤波方法在过去几十年不考虑网络环境的影响下,在状态估计方面得到了广泛的应用,在基本滤波理论的基础上发展了丰富的新方法。然而网络概念的引入使得网络时滞影响下的随机系统状态估计和最优控制成为亟待发展的新问题。因而,针对网络诱发的时滞系统的状态估计和最优问题的研究将具有重要的理论和实践意义[2,3]。为此,研究基于离散时间随机系统在含有测量时滞[4]情况下的最优状态估计问题。提出将时滞系统转化为无时滞系统的方法,并加入均值为零的高斯白噪声,解黎卡提方程得出最优增益,最后得出最优估计方程并完成最优控制器设计,解决网络控制系统的最优估计问题。

1含有测量时滞系统的无时滞转换

考虑如下含有测量时滞和噪声的网络化控制系统:

(1)

其中:x(k)∈Rn为状态向量;u(k)∈Rp为控制输入向量;y(k)∈Rq为测量输出向量;f(k)∈Rm为不可直接测量的扰动向量。A、B、C、D是相应维数的实常数矩阵;h是由传感器引起的测量时滞,为已知的正整数。(·)(k)=(·)(kT),且T为系统的采样周期。

f(k)的动态特性由以下外系统描述:

(2)

T,结合式(1)和式(2)得到状态空间表达式:

(3)

。

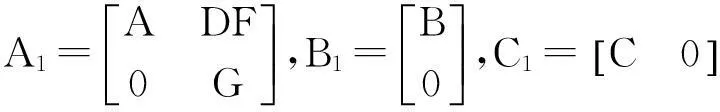
对系统(3),有

(4)

。

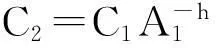
为了对系统进行无时滞转换,我们采用如下基于泛函数的输出转换:

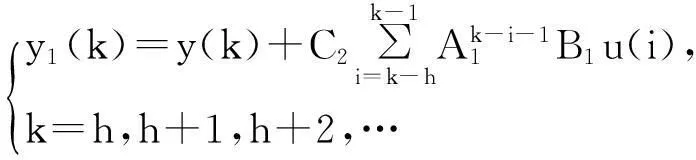
(5)

把式(4)和式(5)代入系统(3),则系统(3)可以转换为以下形式的无时滞系统:

(6)

2最优状态估计器的设计

由于系统存在噪声,想要直接得出真实值十分困难。而卡尔曼滤波[5-9]利用前一状态的已知值在满足最小方差的情况下估计下一状态的值,通过逐步递推得出当前估计值,有效地降低了噪声所带来的影响,对于实时系统更是效果显著。

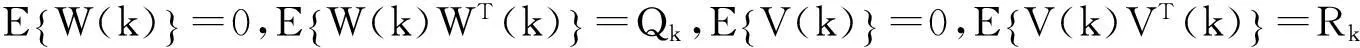
在没有输入u(k)的作用的情况,离散系统的状态方程简化为

(7)

其中:Φ(k+1,k)为从k到k+1的一步状态转移矩阵,考虑估计值可由上一步确定性预测值与修正值相加得到,故可得

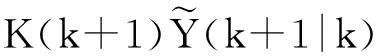
(8)

在Y(k+1)未知情况下对Y(k+1)进行估计,

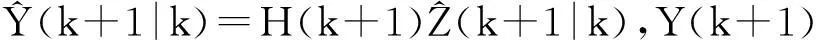
得到滤波方程

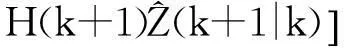
(9)

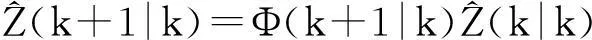
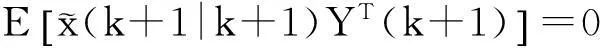
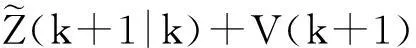
根据以上结果可得

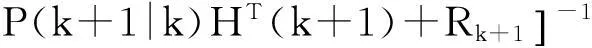
(10)

P(k+1|k)=Φ(k+1,k)P(k|k)ΦT(k+1,k)+

Γ(k+1,k)QkΓT(k+1,k),

(11)

方程(11)即预报误差方差矩阵,但P(k|k)仍未知。

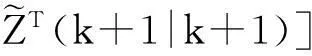
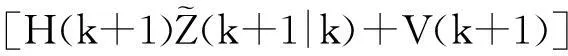
故可得

P(k+1|k+1)=P(k+1|k)-P(k+1|k)×HT(k+1)[H(k+1)P(k+1|k)HT(k+1)+

Rk+1]-1H(k+1)P(k+1|k)=P(k+1|k)-P(k+1|k)HT(k+1)KT(k+1)-

K(k+1)H(k+1)P(k+1|k)+K(k+1)H(k+1)P(k+1|k)HT(k+1)×

KT(k+1)+K(k+1)Rk+1KT(k+1)。

(12)又由式(10)可得增益

K(k)=P(k|k-1)HT(k)[H(k)P(k|k-1)×

HT(k)+Rk]-1,

(13)

从而推得

K(k)Rk=P(k|k-1)HT(k)-

K(k)H(k)P(k|k-1)HT(k),

(14)

由式(12)可得

P(k|k)=[I-K(k)H(k)]P(k|k-1)×

[I-K(k)H(k)]T+K(k)RkKT(k),

(15)

将式(14)代入式(15)得滤波误差方差矩阵

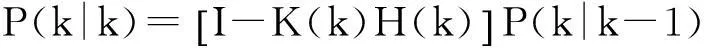
(16)

在对系统进行卡尔曼滤波得出最优估计值后,可对系统进行最优控制器设计,即使系统(6)满足二次型性能指标:

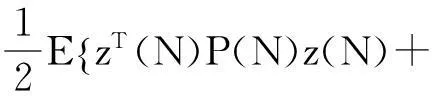
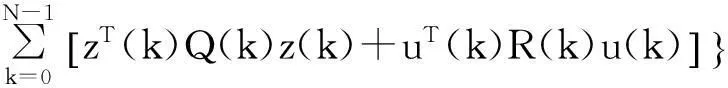
(17)

其中:Q(k)与P(N)为对称非负定矩阵;R(k)为对称正定矩阵。

构造Hamilton函数为

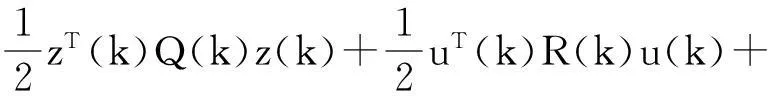
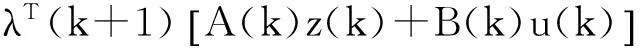
(18)

则由泛函极值存在条件可得最优控制

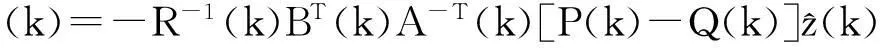
(19)

设

其中:P(k)满足黎卡提方程,则式(19)为

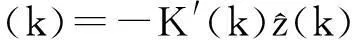
(20)

其中:K′(k)为最优控制反馈增益。

P(k)=ΦT(k+1,k)P(k+1)Φ(k+1,k)-

KT(k)[R(k)+BT(k)P(k+1)B(k)]

K(k)+Q(k)。

(21)

3实例仿真

考虑由式(1)描述的含有时滞的网络化控制系统,其中

考虑由式(2)描述的外系统,其中

取时滞为3,推算得到由式(6)描述的系统中有

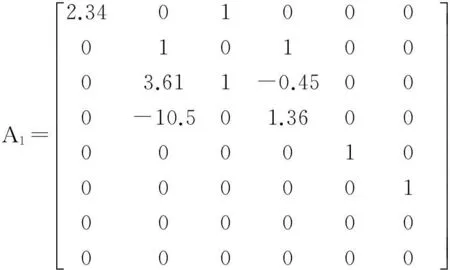
由式(19)和式(21)得

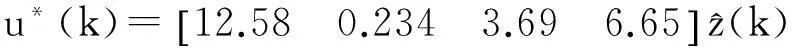
用Matlab进行仿真,结果如图1和图2所示。

图1　系统输入u受振荡环节干扰Fig.1　Interruption of system input u in oscillation link

图2　系统状态响应曲线Fig.2　Response curve of system state

图1、图2中k为离散时间;u为系统输入,受到振荡环节干扰;x为最优状态估计值。由图2可以看出,在系统存在测量时滞和噪声干扰的情况下,系统状态估计x1、x2、x3、x4在经过一个短暂的振荡之后收敛,很快达到稳定状态,得到了满意的控制效果。说明该无时滞转换方法、状态估计及最优控制器设计是有效的。

4结论

针对含有测量时滞的离散时间网络控制系统,利用无时滞转换方法,将含测量时滞的网络控制系统转换为无时滞系统,之后模拟加入高斯白噪声,解黎卡提方程得出最优增益,最后得出最优估计方程,设计得到离散时间情况下随机系统的最优状态控制器。研究采用的无时滞转换方法和最优状态估计的设计思想可推广应用于时变时滞的情况及其他相关问题的解决。

参考文献:

[1]唐斌,刘国平,桂卫华.基于最优预测状态估计的网络化最优控制[J].中南大学学报:自然科学版,2009,40(4):993-1 002.

[2]张冬梅,俞立.线性时滞系统稳定性分析综述[J].控制与决策,2008,23(8):841-849.

[3]高守婉,唐功龙.具有随机丢包的网络控制系统的镇定[J].控制与决策,2011,25(5):690-694.

[4]李娟,赵友刚,于刚,等.含大时滞和噪声的网络化控制系统的最优故障诊断[J].自动化学报,2012,38(5):858-864.

[5]王岩,王夏静,刘翔宇.基于卡尔曼一致性滤波的WSN丢包补偿算法[J].仪器仪表学报,2013,34(11):2 585-2 590.

[6]张友民,戴冠中,张洪才.卡尔曼滤波计算方法研究进展[J].控制理论与应用,1995,12(5):525-538.

[7]张勇刚,黄玉龙,武哲民,等.一种高阶无迹卡尔曼滤波方法[J].自动化学报,2014,40(5):838-848.

[8]Maryam M,Yung F K,Yeng C S.Adaptive Kalman Filtering in Networked Systems with Random Sensor Delays,Multiple Packet Dropouts and Missing Measurements[J].IEEE Transactions on Signal Processing,2010,58(3):1 577-1 588.

[9]Zhang H S,Feng G,Han C Y.Linear Estimation for Random Delay Systems[J].Systems & Control Letters,2011,60:450-459.

Design of Optimal Controller of Discrete-time Stochastic System with Survey Delay

Zhang Pengfei,Zhang Zhi,Liu Xintao

(CollegeofAutomation&ElectronicEngineering,QingdaoUniversityofScience&Technology,Qingdao266042,China)

AbstractThe optimal control problem of the network control system with survey delay in the state of random white-noise was researched in presence of discrete time in allusion to the state estimation and optimization problem of the delay system induced by the network.One state optimal estimation method of the delay system based on the discrete time was proposed,and the design of optimal state estimator was finished at the same time.The method obtained the optimal estimation equation by setting up one system with implication of survey delay first,then transforming the network control system with survey delay as the non-delay system by using non-delay transformation method and estimating the system state by using Kalman filtering method.The method realized state estimation in allusion to the network control system with survey delay and finished design of the optimal controller.Moreover,the feasibility and validity of the method were verified by using the state response of the simulation example system.

Key wordsNetwork control system;Survey delay;Kalman filtering;State estimation;Optimal control

中图分类号:TP273.5

文献标志码:A

文章编号:1004-0366(2016)01-0065-04

作者简介:张鹏飞(1989-),男,山东潍坊人,硕士研究生,研究方向为最优控制.E-mail:wind-fei@163.com.

收稿日期:2015-03-16;修回日期:2015-05-21.

doi:10.16468/j.cnki.issn1004-0366.2016.01.015.

引用格式:Zhang Pengfei,Zhang Zhi,Liu Xintao.Design of Optimal Controller of Discrete-time Stochastic System with Survey Delay[J].Journal of Gansu Sciences,2016,28(1):65-68.[张鹏飞,张志,刘欣涛.含测量时滞的离散时间随机系统的最优控制器设计[J].甘肃科学学报,2016,28(1):65-68.]