水工钢闸门主梁的最优梁高

张雪才，王正中，孟 明，李路明

（西北农林科技大学水利与建筑工程学院，陕西杨凌 712100）



水工钢闸门主梁的最优梁高

张雪才，王正中，孟 明，李路明

（西北农林科技大学水利与建筑工程学院，陕西杨凌 712100）

摘 要：对水工钢闸门主梁高度的确定多以经验公式为主，理论不完善，未全面考虑截面形式与支座位置对梁高影响的问题，依据现行钢闸门设计规范，以满足强度、刚度、稳定性和几何构造要求为约束条件，以主梁和竖向隔板总用钢量最小为目标函数，分别建立单轴、双轴对称截面下的简支式和双悬臂式主梁梁高的优化模型。采用半解析法推导出简支式和双悬臂式主梁的最优梁高理论公式。通过与已建工程对比，结果表明：推导的最优梁高公式计算的梁高均与实际工程中的梁高接近，且公式有进一步优化的空间；通过减小隔板高厚比与主梁腹板高厚比可达到降低梁高的目的。该理论公式一方面可应用于工程实践，另一方面也可为完善规范提供理论基础。

关键词：水工结构；钢闸门主梁；工字形截面最优梁高；优化模型；理论公式

1 研究背景

水工钢闸门是水工枢纽的重要结构之一，其主梁形式以简支式和双悬臂式为主，其最优梁高影响着结构的安全性及经济性。依据结构优化理论，Azad和Vachajitpa等提出了双轴对称工字形简支主梁的经济梁高公式［1－2］；窦国祯给出了单轴对称工字形截面简支梁的经济梁高的图解法和实用公式［3－4］；何运林从196扇闸门资料中拟合出了单轴对称工字形简支梁最优梁高的经验公式［5］；王正中首次提出了双悬臂式单轴对称梁最优梁高的理论公式［6］；随后窦国祯、崔丽萍相继发表了有关双悬臂式钢梁最优梁高的论文［7－8］，其研究思路方法及成果与王正中大同小异。但以上研究成果通用性有限、形式复杂，不便工程应用。鉴于此，本文全面考虑主梁自身的弯剪强度、刚度和整体稳定性及局部稳定性；统一建立了钢闸门主梁最优梁高的优化模型，并利用MATHEMATICA和MATLAB软件对优化模型进行求解，最后给出了对称与不对称工字形简支与双悬臂式钢梁的准确和通用的最优梁高理论计算公式。

2 主梁截面的几何特性

主梁是钢闸门的主要受力构件，一般根据闸门跨度和作用水头来选择其形式［9］。钢闸门主梁的典型截面为单轴对称的工字形截面，其截面、剪应力及弯应力分布图如图1所示。图1（a）是面板承担前翼缘作用组合截面的剪应力分布图，图1（b）是部分面板参加主梁工作而形成的组合工字形截面，图1（c）是主梁工字形截面的弯应力分布图。

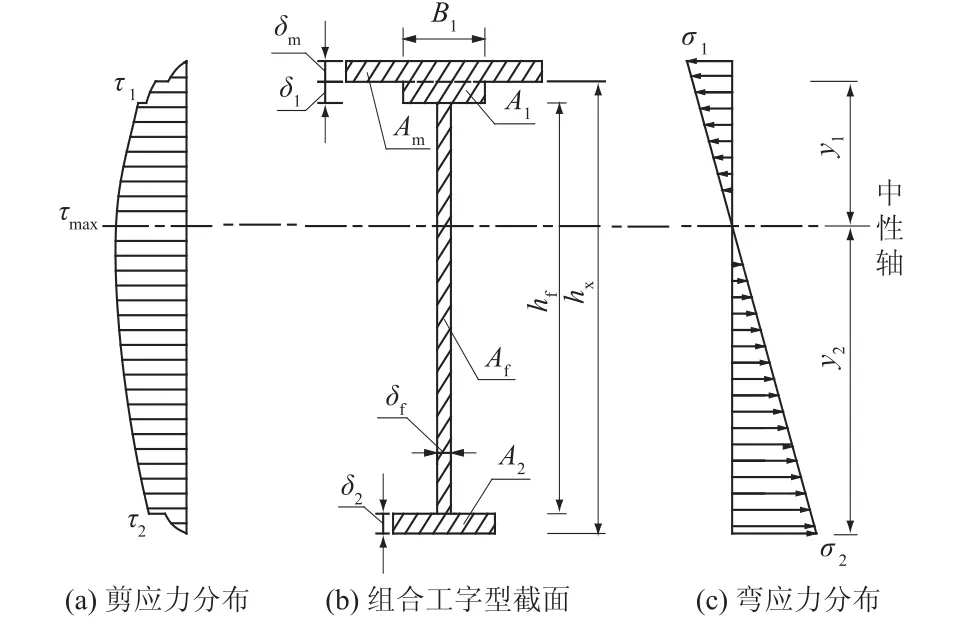
图1　主梁典型计算截面及应力分布Fig．1 Typical calculation section and stress distribution of main beam

图1中：A1为前翼缘面积；A2为后翼缘面积；Af为腹板面积；Am为参与主梁工作的部分面板面积；A1m＝A1＋Am为前翼缘面积和参与主梁工作的部分面板面积的和；hx为主梁高度；hf为腹板高度；y1为中性轴到前翼缘外侧的距离；y2为中性轴到后翼缘外侧的距离；σ1为前翼缘外侧处的正应力；σ2为后翼缘外侧处的正应力；τ1为前翼缘外侧处的剪应力；τ2为后翼缘外侧处的剪应力；τmax为腹板上的最大剪应力；δm为面板厚度；δ1为主梁前翼缘厚度；δ2为主梁后翼缘厚度；δf为主梁腹板厚度；B1为主梁前翼缘宽度。本文中各物理量的单位分别为：面积（mm2），高度（mm），应力（MPa），面积抵抗矩（mm3）。

实际工程中，面板厚度与主梁高度的比值几乎都在［1／60，1／140］范围，故可认为面板的厚度远远小于主梁的高度，可设hx≈hf。令

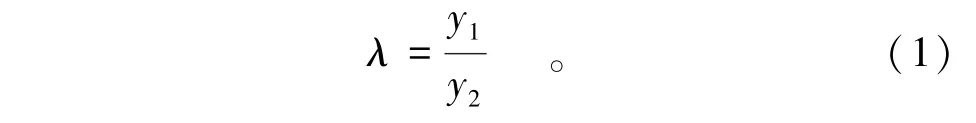
根据《钢结构设计规范（GB50017—2003）》［10］，对只受弯矩控制的闸门主梁来说其腹板的高厚比由局部稳定条件确定，可设＝ψ。

根据式（1）和截面几何特性的定义，对中性轴求惯性矩，忽略高阶微量简化得：

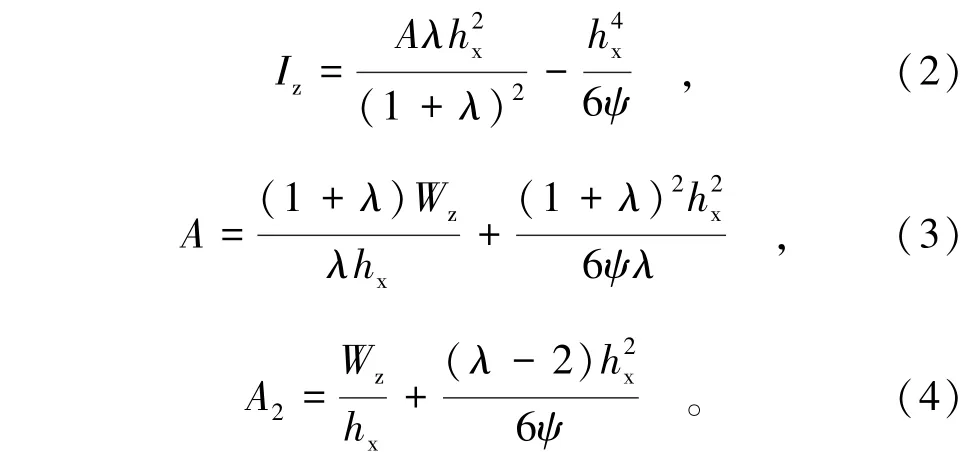
后翼缘对中性轴的面积矩为

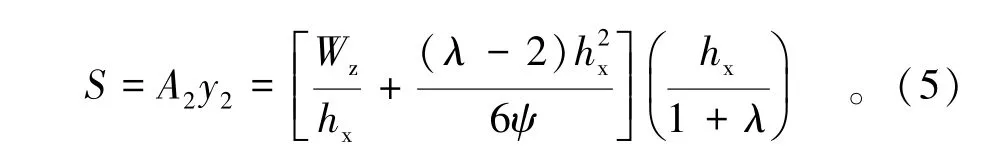
式中：A为主梁和参与主梁工作部分面板的面积之和；Wz为中性轴的面积抵抗矩。

3 约束条件

3．1 强度约束

主梁的设计必须满足强度要求，即σmax≤［σ］。主梁后翼缘最大正应力为，主梁后翼缘与腹板焊接处的切应力为。其中：σmax和[σ ]分别为主梁的最大弯应力和允许应力（MPa）；M为主梁后翼缘处弯矩（kN·m）；Fs为主梁支座截面处的剪力（kN）；ymax为离中性轴最远点的距离（m）。

满足强度条件为

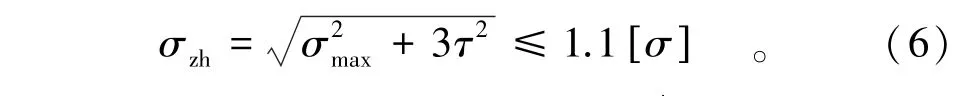
式中σzh为主梁的折算应力，令，可得

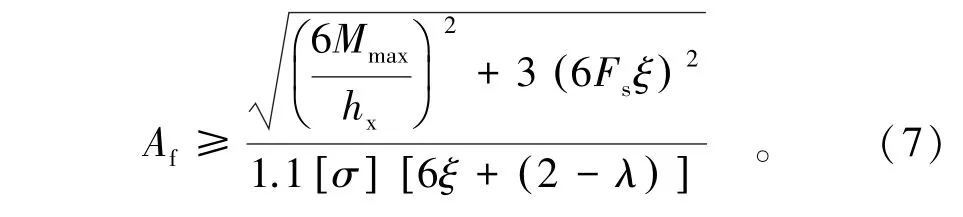
3．2 刚度约束

双悬臂式主梁，由于其最大挠度较小，在一般情况下，这种形式的闸门主梁的刚度条件对梁高不起控制作用。

3．3 稳定性约束

主梁整体稳定性和腹板局部稳定性依据主梁的受压翼缘与刚性面板相连，因而主梁的整体稳定性可不必验算。腹板局部稳定性关系到其高厚比的预先设定、横向加劲肋的配置以及是否配置纵向加劲肋，可先根据《钢结构设计规范（GB50017—2003）》的规定，根据高厚比限值条件确定腹板及横、纵向加劲肋的配置。

4 简支梁最优梁高公式

4．1 目标函数

根据结构优化设计的基本思想建立求最优梁高的优化模型［11］。虽然闸门的面板是与主梁的前翼缘焊接在一起的，但参与主梁发生整体弯曲部分面板的截面主要是由设计水头、结构布置、有效宽度等事先确定，所以参与主梁工作面板的面积Am在推导过程中为一确定的参数。用F1和F2分别表示主梁和隔板的质量；用l1和l2分别表示主梁和隔板腹板的化引长度（即主梁与隔板腹板化成等高截面后的长度）；用n1和n2分别表示主梁和隔板的个数。不考虑钢材的变异性［12］，仅按理想的材料特性进行计算，设隔板总长与主梁总长的比值为K；隔板高厚比为m，则以单位主梁长上质量最小作为优化目标的表达式为

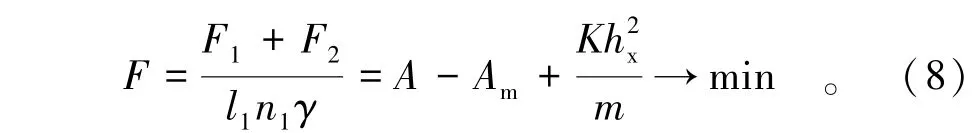
4．2 简支梁的优化模型

由目标函数和约束条件可得简支梁的优化模型为

式中：Sm＝A1，min＋Am，min为计算截面中参与主梁工作的面板的面积和前翼缘截面面积之和的最小容许值；λmax为主梁前、后两翼缘在整体弯曲中的抗弯应力绝对值之比的最大容许值，因为面板参与主梁的工作，所以面板的应力应该与主梁前翼缘外表面在梁的整体弯曲中产生的应力以某一种形式相互叠加，叠加后的应力共同对面板起作用，而后翼缘外表面的应力没有叠加问题，所以在梁的整体弯曲中应使得前翼缘的应力与后翼缘的应力的比值不能过大，以此来满足面板处的强度条件，因此λmax＝，其中α为弹塑性调整系数，取值1．4或1．5；σmy为垂直于主梁轴线方向板支撑长边中点的局部弯曲应力。

4．3 模型求解及简支梁最优梁高

由约束条件可得图2，图中阴影线左侧的为可行域，右侧为非可行域。图中h′为主梁截面前翼缘能够达到极限应力状态的各种梁高的最大值。由于受到参与主梁工作面板面积和前翼缘截面面积之和最小容许值Sm的限制，当实际梁高大于h′，前翼缘就无法达到极限应力状态，又因为λmax＜1，hx≥0，故可行域内各点的λx之值一定在（0，1）内，当λx∈（0，1），则由目标函数的单调性及其表达式可以看出，对hx任意固定不变的值，F的值均随着λx的增大而减小，得到F取不同值时的曲线，可以看出，最优点一定在可行域右边的边界上。其中F1＜F2＜F3＜F4。

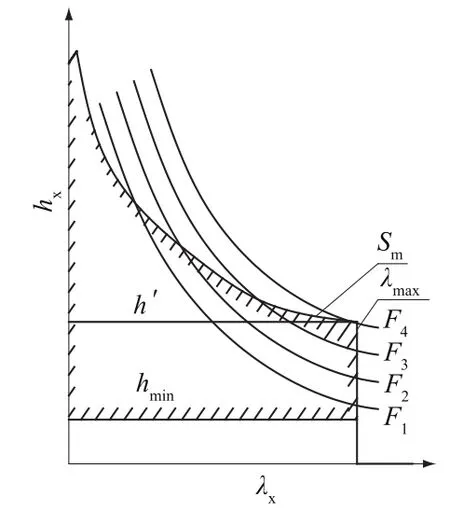
图2　约束条件及目标函数Fig．2 Constraint condition and objective function

当前翼缘外侧应力σ1达到最大值，即λx＝λmax，hmin＜hx＜h′，目标函数可变为

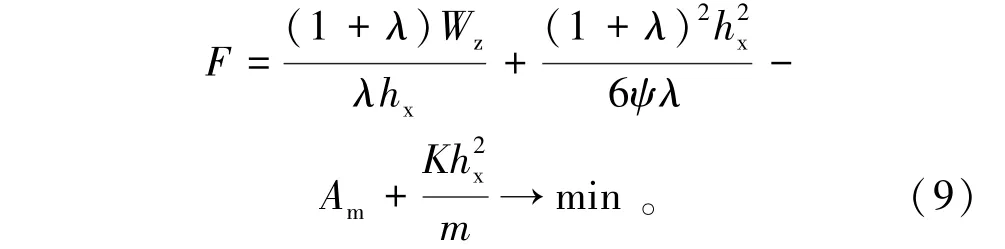
hx＝

不考虑面板影响时即双轴对称，此时λ＝1，可得主梁的最优梁高为

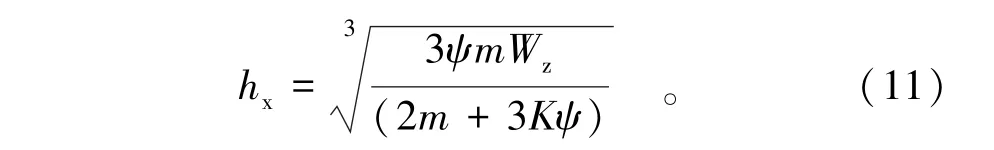
式（10）和式（11）即为简支型主梁最优梁高计算式，各参数意义如前面所示，hx单位为mm。

5 双悬臂梁最优梁高公式

5．1 双悬臂型主梁优化模型

目标函数同前，其优化模型中Ms，Fs分别为主梁与支臂连接处的弯矩的绝对值（kN·m）和剪力值（kN）。

5．2 模型求解及双悬臂主梁最优梁高

该模型取得极小值的必要条件为

当λx∈（0，1）时，F′λx＜0，为单调递减函数，又因为λx在[0．75，0．95]内目标函数的差别极小，参考《水利水电工程钢闸门设计规范（SL74—2013）》［13］和关于面板弹塑性调整系数研究成果［14］，前、后翼缘外侧弯应力绝对值之比宜取λx＝0．8，将其代入式（12）和式（13）可得：

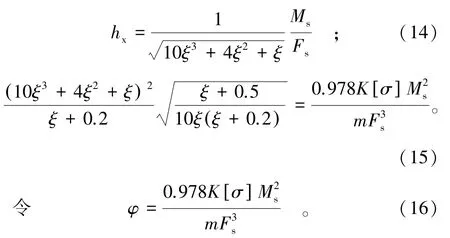
对实际工程统计分析可得：0．1≤φ≤80，采用MATLAB进行处理可得到φ和ξ的关系式为

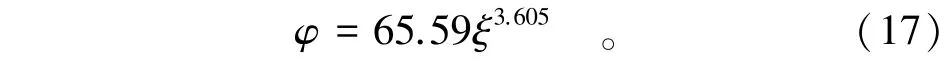
确定系数为0．999 7。联立式（14）至式（17）得到

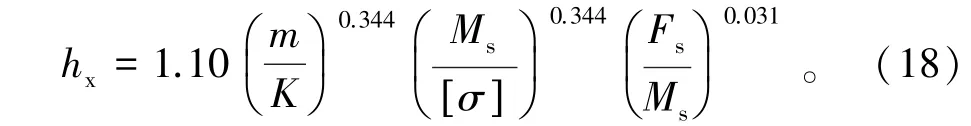
根据《水利水电工程钢闸门设计规范（SL74—2013）》双悬臂式主梁的悬臂长度宜取0．2l（l为主梁的计算跨度），此时，代入式（18）可得

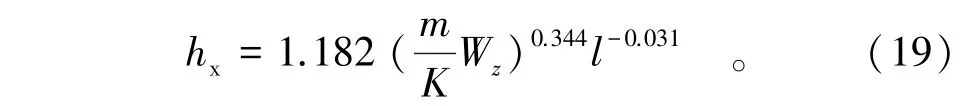
对双轴对称双悬臂式主梁，此时λx＝1，将其代入式（12）和式（13），同理得到

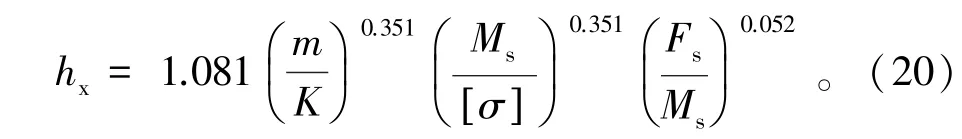
当悬臂长度为0．2l，代入式（20）可得

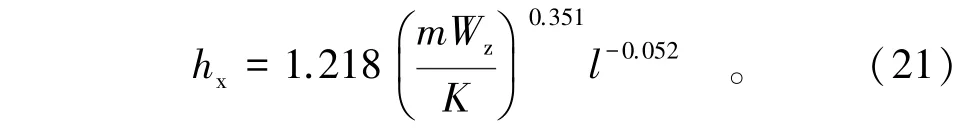
上式中m，K，Wz，l均为常数，其中单位规定：Fs为kN；Ms为kN·m；σ为kN／m2；l为m；h为mm。

式（18）和式（20）即为双悬臂式主梁最优梁高计算式，各参数意义如前面所示，为保证计算精度，小数点后均保留3位数字。

6 简支型和双悬臂型主梁梁高公式的验证

本文搜集到已建工程5例（均为单轴对称简支梁）如表1所示。

某表孔斜支臂弧门孔口尺寸12．0 m×6．55 m（宽×高），m为80，λ为0．8，［σ］为144 000 kPa，横主梁2根，横隔板5道，Ms为387 kN·m，Fs为455 kN。实际工程中的梁高为0．6 m。

利用推导式（18）和式（19）求解可得最优梁高分别为0．585 m和0．579 m，利用文献［7］中公式（47）求解的最优梁高为0．604 m。

7 结 论

由以上工程实例验证可得：

（1）利用本文推导的最优梁高公式计算的梁高均与实际工程中的梁高接近，对简支式最大误差不超过10%，双悬臂式误差仅为2．5%，且计算方便简捷。

（2）横隔板的高厚比、主梁腹板的高厚比均与主梁高度成正相关关系，也即隔板多而厚时最优梁高降低，反之，最优梁高就增大。

（3）文献［4］和文献［7］中的计算公式均需要进行查表补差，会带来一定的误差，本文公式不需要查表，可克服查表时带来的插值误差。

（4）文献［5］直接利用经验公式h＝5．1W1／3进行求解，计算方便，但公式推导过程中没有比较完整的数学模型，与之相比，本文公式推导有完整的数学模型和完善的理论基础。

本文以设计规范为依据，以满足强度、刚度、稳定性和几何构造要求为约束条件，应用结构优化理论，全面系统地推导出闸门主梁高度的计算公式。公式中的各个参数在设计闸门时事先可以确定，进而可以确定最优的梁高，可以克服设计中的盲目性，减少工作量。通过与文献［4］、文献［5］、文献［7］和已建工程实例的对比，验证了本文所推公式的正确性及合理性，且本文公式的推导理论明确，概念清晰，计算过程方便简捷，不仅可供工程设计参考，而且还可为规范的完善提供理论基础。

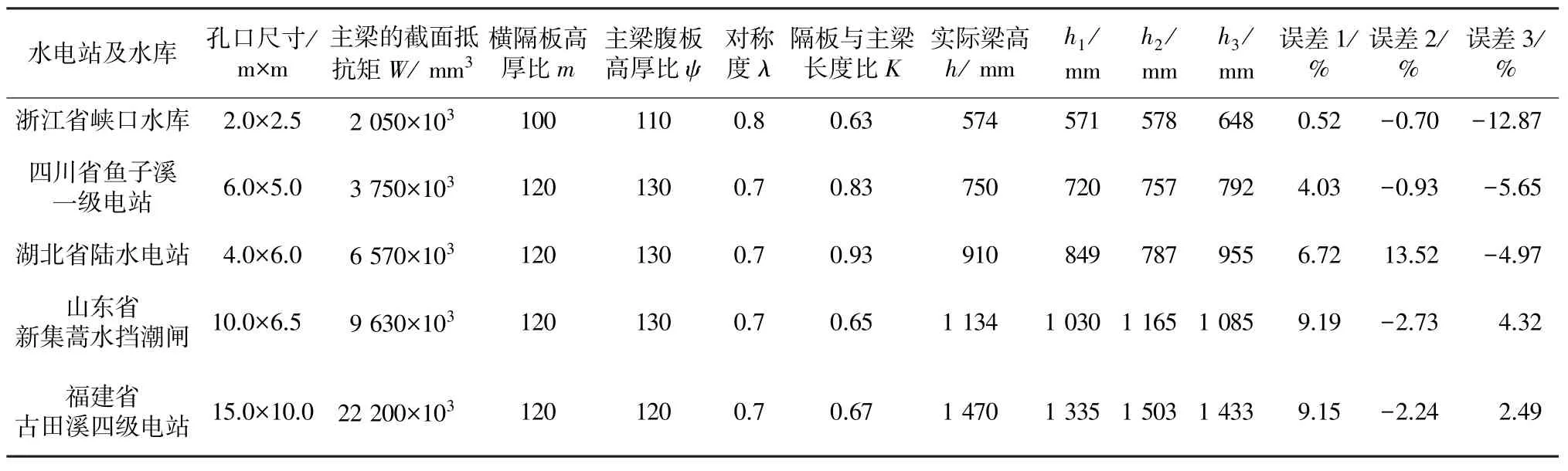
表1　本文公式计算结果与实际工程梁高对比分析Table 1 Comparison of height of the main beam between calculated result and data in practical projects

参考文献：

［1］ AZAD A K．Economic Design of Homogeneous I－Beams ［J］．Journal of the Structural Division，1978，104（4）：637－648．

［2］ VACHAJITPAN P，ROCKEY K C．Design Method for Optimum Unstiffened Girders［J］．Journal of the Structur⁃al Division，1978，104（1）：141－155．

［3］ 窦国祯．水工钢闸门主梁的经济梁高［J］．水运工程，1979，36（11）：1－8．

［4］ 窦国祯．钢闸门最优梁高计算公式［J］．水力发电学报，1991，10（1）：35－45．

［5］ 何运林．钢闸门不等翼缘钢梁的最优梁高［J］．水力发电学报，1992，11（2）：39－51．

［6］ 王正中．弧形双悬臂主梁最优梁高［C］∥安玉杰，钱学智，李俊杰．水工结构工程理论及应用．大连：大连理工大学出版社，1993：109－115．

［7］ 窦国祯．斜支臂弧形闸门的经济梁高［J］．水力发电，1994，61（5）：34－38．

［8］ 崔丽萍．钢闸门主框架梁梁高优化设计［J］．水力发电学报，2011，30（5）：175－178．

［9］ 安旭文，侯建国，李大庆．水工平面钢闸门主梁的可靠度校准分析［J］．长江科学院院报，2003，20（1）：13－16．

［10］GB50017—2003，钢结构设计规范［S］．

［11］王光远，董明耀．结构优化设计［M］．北京：高等教育出版社，1987．

［12］周建方，李典庆．水工钢闸门结构系数的确定［J］．长江科学院院报，2002，19（5）：34－37．

［13］SL74—2013，水利水电工程钢闸门设计规范［S］．

［14］王正中，徐永前．对四边固支钢面板弹塑性调整系数理论值的探讨［J］．水力发电，1989，8（5）：39－42．

（编辑：刘运飞）

Optimal Height of Main Beam of Hydraulic Steel Gate

ZHANG Xue⁃cai，WANG Zheng⁃zhong，MENG Ming，LI Lu⁃ming
（College of Water Resources and Architecture Engineering，Northwest A＆F University，Yangling 712100，China）

Abstract：At present，there are several problems in determining the height of main beam in hydraulic steel gate，in⁃cluding a large number of empirical formulas，imperfect theories，and ignorance of influences of section form and support position．According to design code of steel gate，with requirements of strength，stiffness，stability and geo⁃metric structure as constraint conditions，we take minimum steel amount of main beams and vertical baffles as ob⁃jective function，and establish optimization models for beam height of simple support and double cantilever’s girder under conditions of uniaxial and biaxial symmetrical sections．Theoretical formulas of optimal girder height are de⁃rived by semi⁃analytical methods．Through comparing with built projects，we find that girder heights calculated by the theoretical formulas in this paper are close to those in practical projects，which still can be optimized．Further⁃more，we can decrease beam height through reducing height⁃thickness ratios of partition and web of main beam．The theoretical formulas can be applied to engineering practice，and also provide a theoretical basis for improving speci⁃fication．

Key words：hydraulic structure；main beam of steel gate；optimal height of H⁃shaped beam；optimization model；theoretical formula

通讯作者：王正中（1963－），男，陕西彬县人，教授，博士生导师，主要从事水工程安全及其灾害防治理论与技术研究，（电话）13319210121（电子信箱）wangzz0910＠163．com。

作者简介：张雪才（1990－），男，河南项城人，硕士研究生，主要从事水工结构稳定及优化研究，（电话）15202495509（电子信箱）xnzxc1990＠163．com。

基金项目：国家自然科学基金项目（51179164）

收稿日期：2014－09－15；修回日期：2014－12－04

中图分类号：TV663．4

文献标志码：A

文章编号：1001－5485（2016）03－0127－05