城市工业用地产出率影响因素及区域比较——地级城市面板数据分析

许明强

（1.成都大学旅游与经济管理学院，四川 成都 610106 2.西南财经大学应用经济学博士后流动站，四川 成都 610074）

城市工业用地产出率影响因素及区域比较
——地级城市面板数据分析

许明强1，2

（1.成都大学旅游与经济管理学院，四川 成都 610106 2.西南财经大学应用经济学博士后流动站，四川 成都 610074）

研究目的：发现城市工业用地产出率影响因素及其影响程度和区域差异，提出相应对策以促进工业集约用地。研究方法：根据土地功能理论和经济主体动力学关系导向原则构建城市工业用地产出率双向固定效应模型，利用地级城市面板数据估计并检验工业用地产出率影响因素及作用程度并进行区域比较。研究结果：城市工业用地投资强度、就业密度和全要素生产率对1999年来城市工业用地产出率增长的贡献率分别为21.3%、-7%和85.7%；它们对工业用地产出率的边际贡献由于东中西部工业用地集约度、产业类型、劳动素质不同而呈现出区域差异。研究结论：应遏制各地尤其是中西部工业新区建设中粗放用地行为、促进工业投资并加强工业区生活配套以提升投资强度和就业密度，应在工业用地配置和评价中更加重视全要素生产率指标，应推动中西部地区工业升级并在营商环境、基础设施等方面缩小与东部的差距。

土地利用；全要素生产率；双向固定效应；工业用地产出率；投资强度；就业密度

1 引言

如何抑制工业粗放用地现象以提升城市工业用地产出率，是中国城镇化和工业化进程中面临的重要问题。习近平、李克强都鲜明地批评了工业园区铺大摊子和城镇土地低效利用问题[1-2]，即便在中国工业化先行区上海和厦门等地，工业用地产出率亦偏低[3-4]。在政策实践上，遵循《工业项目建设用地控制指标》（国土资发［2008］24号）等政策法规的精神，工业用地固定资产投资强度被作为各地方政府招商引资的重要门槛，那么，重视投资强度的政策究竟在多大程度上推进了工业用地高效产出？除了投资强度，其他因素——工业就业密度、全要素生产率（TFP）又在多大程度上影响了工业用地产出率的提升？它们有何区域差异？

在CNKI和EBSCO数据库检索发现近几年来关于工业用地利用效率影响因素问题的文献逐渐增加，这些文献发现投资强度、就业密度、全要素生产率、土地市场化、政府竞争、区位、产业结构等都是工业用地产出率的重要影响因素，这些因素可分为直接因素和间接因素两大类，间接因素通过影响直接因素进而影响用地效率。关于直接因素——投资强度、就业密度和TFP的研究观点包括：（1）工业用地地均资本对产出率的弹性系数为0.346，地均劳动对它的弹性系数为0.142[5]，容积率和投资强度达不到建设控制标准[6-8]、工业园土地供需比例过高[9]、土地和劳动力投入冗余[10-11]使得工业用地效率较低；（2）全要素生产率（TFP）尤其是技术进步对工业用地产出率具有重要影响[12-13]，对2001—2012年工业用地生产效率实证研究表明全国总体和绝大多数省份的工业全要素生产率呈递增趋势[14]。

关于间接因素的研究观点包括：（1）工业用地市场化改革能显著提高中国工业用地利用效率，政府干预会降低城市工业用地效率[15]，应减少地方政府对工业用地出让程序和出让价格的干预[16-17]；（2）工业用地价格调控可以有效促进工业用地集聚，从而提高工业用地效率[18]；（3）不能忽视废水废气等工业非期望产出，否则会高估工业用地生产效率[19]，需通过产业升级以提升工业用地效率[20]；（4）政府竞争对城市工业用地利用效率有明显影响[21]；（5）区位因素与土地利用效率紧密相关，城市化率更高的地区比外围地区更能实现工业用地高效利用[9]，需促进制造业的空间布局优化[22]，与区位因素类似的还有土地等别影响用地效率的观点[23]。

在工业用地产出率研究中的计量经济模型设计上，较多学者采用了生产函数模型，不过土地要素在工业生产函数中出现的形式并不统一。（1）土地属于资本：在柯布—道格拉斯（Cobb-Douglas）模型的原形中，在索洛[24]、肯德里克[25]和周方[26]关于生产函数的分析中，土地作为资本的一部分并不单独出现。（2）土地与其他要素并列：丹尼森[27]、陈利根和龙开胜等[12]、林荣茂和刘学敏[28]、杨杨和吴次芳等[29]、王克强和熊振兴等[30]、李谷成[31]等学者将土地和劳动、资本并列纳入生产函数中作为产出的解释变量①李谷成、陈利根和龙开胜在规模报酬不变的假设下将该函数变换为地均产出关于地均资本和就业密度的函数形式，但这种假设与其推导出的函数形式不能兼容。。（3）土地为其他要素的分母：在少数学者构建的生产函数中，土地是作为产出、投资和劳动的分母出现的，比如Antonio Ciccone和Robert E. Hall[32]、黄大全和梁进社[33]、林坚和张沛等[23]。

文献梳理表明，当前关于工业用地产出率的研究不仅包括了具有基础影响的直接因素，也深入到了这些直接因素背后的影响因素。不过，关于直接因素的研究更需要得到重视，因为：（1）仅有很少成果呈现了投资强度、就业密度和TFP各因素对城市工业用地产出率的具体影响程度；（2）对各影响因素地位的观点仍然存在分歧，比如，吴群教授等认为容积率和投资强度达不到建设控制标准是工业用地投入损失的主要原因[8]，陈利根等认为技术进步和投资强度是更主要因素[12]，而郭贯成和熊强认为工业行业技术水平对城市工业用地效率的影响还有待检验[34]；（3）现有文献大多利用省级面板数据展开研究，仅有个别学者利用地级以上城市工业用地相关数据展开研究；（4）土地要素在工业生产函数中出现的形式并不统一，如何在工业生产函数中以恰当的形式反映工业用地的作用。

本文将以适当的方式在柯布—道格拉斯生产函数（C-D函数）中反映土地要素的作用，基于中国地级城市工业面板数据，构建双向固定效应模型，探讨投资强度、就业密度和TFP对工业用地产出率的影响程度，并提出政策建议。

2 模型

如上所述，在工业生产函数模型构建时，有的学者把土地视为资本的一部分将其纳入资本之中，但是这与农业领域不一样，土地在工业生产过程中并不发生消耗和转移，工业用地与资本具有不同属性，将其纳入资本必须满足一个很强的假设条件：工业用地总是与资本和劳动相匹配的，恰好满足资本和劳动的承载需要——这显然不符合实际。有的学者将土地与资本和劳动要素并列，但在工业生产领域，“土地主要是作为地基、操作的场地与空间发挥作用”[35]，在劳动和资本的土地承载需求得到满足的正常生产情况下，土地对于劳动和资本不存在真正意义上的边际替代关系，比如如果减少资本投入，无论增加多少土地都无法实现工业产量不减少。所以，在工业生产函数中把土地作为资本的一部分，或者将资本、劳动和土地三要素并列作为产出的解释变量都是不够妥当的，应将工业用地作为其他要素的分母。另外，根据经济主体动力学关系导向原则[36]，模型解释变量应由被解释变量的直接影响因素担任，间接因素与直接因素共同作为解释变量的做法会带来多重共线性等问题。由此发展C-D函数构建工业用地产出率面板模型（式（1））：

式（1）中，yit为城市工业生产总值，mit为城市工业用地，kit为城市工业固定资产，lit为城市工业就业量，α和β分别为地级城市工业用地投资强度和就业密度②为表述方便，下文一般将“地级城市工业用地投资强度”、“地级城市工业用地就业密度”、“地级城市工业用地产出效率”简称为“投资强度”、“就业密度”、“产出效率”。的产出弹性。Ait为中性技术进步，是“生产函数任意一种形式变动的简称”，“经济的加速或减速、劳动力教育质量的改进、各种各样移动生产函数的因素都可归入‘技术变化’之中”[24]，这种技术进步既随时间而变，也可能因个体而异。

这里讨论工业用地单位面积上的资本、劳动和产出，相当于控制土地要素投入使其保持不变，适用边际报酬递减规律，所以α + β＜1。也就是说，在包括技术在内的其他条件不变的情况下，如果让一块正常发挥承载功能的工业用地的投资强度和就业密度同时增加φ倍（φ＞0），其产出率的提高幅度φα+β将在开区间（0，φ）之内。

考虑到样本点的个体特征、不可观测的遗漏变量和数据获得性问题设计以下工业用地产出率双向固定效应模型：

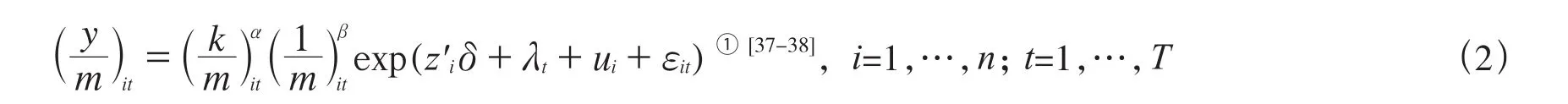
式（2）中，λt为不随个体变动但随时间而变的时间固定效应，包括技术进步、宏观经济变动、产业政策影响等变量；zi为不随时间而变的个体特征变量向量，ui为不可观测的个体异质性，表示不随时间变动但随个体变动的遗漏变量，它与zi的差别在于“不可观测”，z'iδ + ui= ηi为全部不随时间而变的个体固定效应，包括区位、自然环境、历史人文环境等变量；ui+ εit构成复合扰动项。

对模型（式2）两边取对数得：

3 数据与描述性统计

出于样本代表性和经济性的考虑，采用分层抽样的方法从全国27个省级行政区②不包括北京、上海、天津和重庆4个直辖市。中按1/3比例抽取地级城市样本点，当“层个体数×1/3”不为整数时，采用舍弃小数的办法确定层样本量，得到包含93个城市的总样本，其中东部城市29个，中部城市31个，西部城市33个。从《中国城市统计年鉴》、《中国城市建设统计年鉴》或《中国城市建设统计年报》中采集1998③因为《中国城市建设统计年鉴（年报）》自1998年开始编制，笔者没有发现获得1998之前年份城市工业用地数据的其他途径。—2014年各样本城市市区的工业用地、工业就业、工业企业固定资产和工业总产值等数据形成短面板数据。

关于解释变量和被解释变量的指标选取具体说明如下：（1）选取地级城市市辖区数据进行分析，有利于排除因为城市层级不同而形成的差别，有利于排除城市工业与乡镇工业和独立工矿区工业的差别，从而增强数据的可比性；（2）工业就业、固定资产和总产值只能得到规模以上工业数据，和工业用地之间不完全匹配，鉴于地级城市规模以下工业企业占地数量少，在各类工业发展数据中占比也很小，假定它对本文研究产生的偏误在可接受的范围之内；（3）投资强度采用“工业固定资产/工业用地面积”得到，没有以“年度工业投资/工业用地面积”衡量， 一方面因为所有固定资产都参与了工业生产，另一方面这也是工业用地评价实践的做法；（4）工业固定资产为经过扣减折旧、减值准备之后的期末余额；（5）由于地级城市市辖区缺乏部分年份的工业增加值统计数据，采用“规上工业总产值/工业用地面积”衡量市辖区工业用地产出率；（6）以 “工业就业人数/工业用地面积”衡量就业密度。

数据处理工作包括：（1）根据《中国统计年鉴》计算GDP平减指数，然后把历年工业生产总值、固定资产价值都按照1990年价格进行折算，以实现可比性；（2）对样本个体时间序列中个别遗漏数据、明显畸高或畸低的数据，推断其出现统计工作失误，以该样本点前后年份数据的平均值代替，或以之前几年的平均增速推断；（3）如果样本点的某一变量出现连续2年以上的明显异常值或缺漏值，则删除该年份观察值；（4）以普通箱形图——以“75%分位数+1.5倍4分位间距”为箱形图上侧內篱笆，以“25%分位数－1.5倍4分位间距”为箱形图下侧內篱笆——找出离群值并删除。

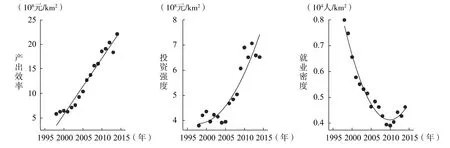
图1 城市工业用地产出率、投资强度、就业密度变化趋势Fig.1 The change trend of urban industrial land productivity, investment intensity and employment density

观察历年样本均值，可以发现产出率和投资强度呈现逐年上升态势，而就业密度则呈总体下降态势（图1）。直观显示，工业用地投资强度对产出率存在积极贡献，而就业密度可能存在负的影响，就业密度的下降态势折射出持续的技术进步等全要素生产率的存在，后者可能是影响工业用地产出率的重要因素。

为了回归分析的需要，对地级城市工业用地产出率、投资强度和就业密度数据取自然对数，基本统计特征如表1所示。整体上看，各变量均值和中位数很接近，偏度接近0，峰度接近3，近似正态分布。

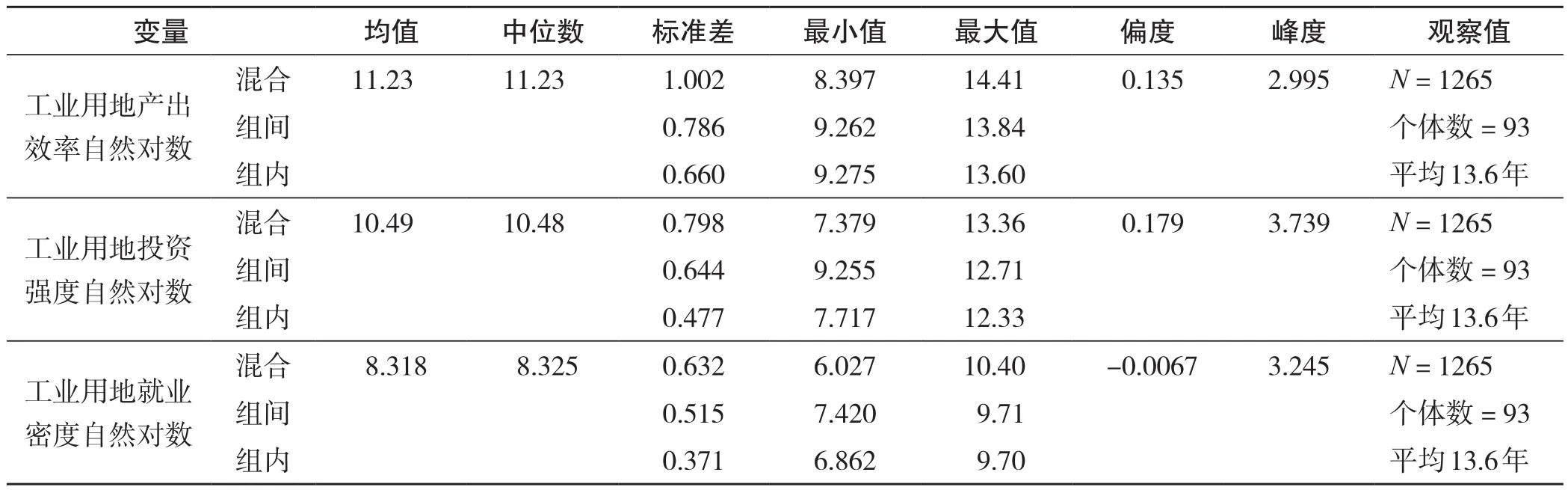
表1 基本统计量Tab.1 Basic statistics

4 参数估计、模型检验

4.1 混合回归还是个体效应：F检验和LSDV检验

首先对模型（式（1））等式两边取对数，通过stata 13按固定效应模型（FE）估计且不采用聚类稳健标准误，进行F检验，发现F（92，1170） = 16.93，p值为 0.0000，强烈拒绝不存在个体效应的原假设，应允许各样本个体拥有自己的截距项。对模型（式（1））增加个体特征并将其视为参数，对每个样本个体定义一个虚拟变量，然后把92个个体虚拟变量纳入回归方程中（未包括的第一个个体虚拟变量为共同截距项），取自然对数后得到：

式（4）中，个体虚拟变量d2i= 1，如果i = 2；d2i= 0，如果i≠2；以此类推。采用最小二乘虚拟变量（LSDV）法回归式（式（4）），发现绝大多数个体的虚拟变量都很显著，所以拒绝“所有个体虚拟变量都为0”的原假设，认为存在个体效应。

4.2 随机效应还是固定效应：豪斯曼检验和过度识别检验

根据反映个体异质性的遗漏变量ui与其他解释变量是否相关，个体效应的形态可分为固定效应和随机效应，有必要通过检验在二者之中做出选择。通过豪斯曼检验（Hausman test），得到χ2（3）等于21.36，p值为0.0001，故拒绝原假设“H0：ui与xit、zi不相关”，宜采用固定效应模型而非随机效应模型。鉴于豪斯曼检验不采用稳健标准误，隐含一个比较强烈的假设——ui与εit都是独立同分布的，而且通过估计发现聚类稳健标准误和普通标准误存在较大差异，豪斯曼检验效果值得质疑，有必要开展进一步检验。随机效应模型和固定效应模型相比，多了“个体异质性ui与解释变量xit、zi不相关”的约束条件，可以视为过度识别条件，所以用xtoverid命令进行过度识别检验（overidentification test），得到统χ2（2）计量为12.437，p值为0.0020，拒绝随机效应，应采用固定效应模型。

4.3 双向固定效应估计和检验

固定效应包括个体固定效应和时间固定效应，个体固定效应模型可解决不随时间而变但因个体而异的遗漏变量问题；那些不随个体改变但因时间而异的遗漏变量问题则需要引入时间固定效应予以解决。上述LSDV检验表明，个体固定效应确实存在，但工业用地就业密度对产出率的弹性系数为-0.513，标志着就业密度对产出率存在负的边际效应，这与生产理论和实践相悖。所以，有必要同时考虑时间固定效应的影响，估计双向固定效应（Tow-way FE）模型（式（3））得到的结果见表2。

表2 城市工业用地产出率双向固定效应模型估计Tab.2 Regression of tow-way fixed effect model of urban industrial land productivity

表2显示，多数年份虚拟变量的系数在1%的水平上显著，少数年份不显著，对时间虚拟变量系数进行Wald检验得到统计量F（16，92） = 41.69，p值为0.0000，强烈拒绝不存在时间效应的原假设。同时，工业用地就业密度对产出率的弹性系数估计为0.181，不再呈现负数，具有了与生产理论和实践相吻合的经济意义：在其他条件不变的情况下，就业密度每提高1%，可使产出率提高0.181%。而且，双向固定效应估计的拟合优度达到0.842，明显高于FE估计的拟合优度0.594。此外，联合检验表明工业用地投资强度的和就业密度弹性系数之和小于1，印证了上文的系数约束假设，反映了其他条件不变前提下单位面积工业用地上资本和劳动要素边际报酬递减的规律；这种系数约束特征也可以从它们的95%置信区间［0.411，0.670］和［0.047，0.316］直观发现。综上，双向固定效应模型（式（3））及其估计结果是可信的。

这里得到的工业用地产出率的投资强度弹性系数为0.541，高于林坚和张沛的0.282、张琳和王亚辉的0.346；就业密度弹性系数为0.181，介于林坚和张沛[23]的0.346与张琳和王亚辉[5]的0.142之间。这种区别可能是由于数据不同形成的，林坚和张沛使用的是国家级开发区数据，笔者分析的是地级城市数据，一般而言，地级城市工业区比国家级开发区的资本更稀缺、投资强度更低，会推高投资强度弹性系数；地级城市工业职工比国家级开发区职工平均劳动素质存在一定差距，会拉低就业密度弹性系数。因此，这种弹性系数的差别有助于印证双向固定效应模型（式（3））及其估计结果的可信度。

4.4 分区域聚类回归分析

利用中国东部、中部和西部的数据分别对模型（式（3））做回归，与全国样本数据回归结果做对照，可以进一步检验Two-way FE估计的稳健性，其回归结果见表3。

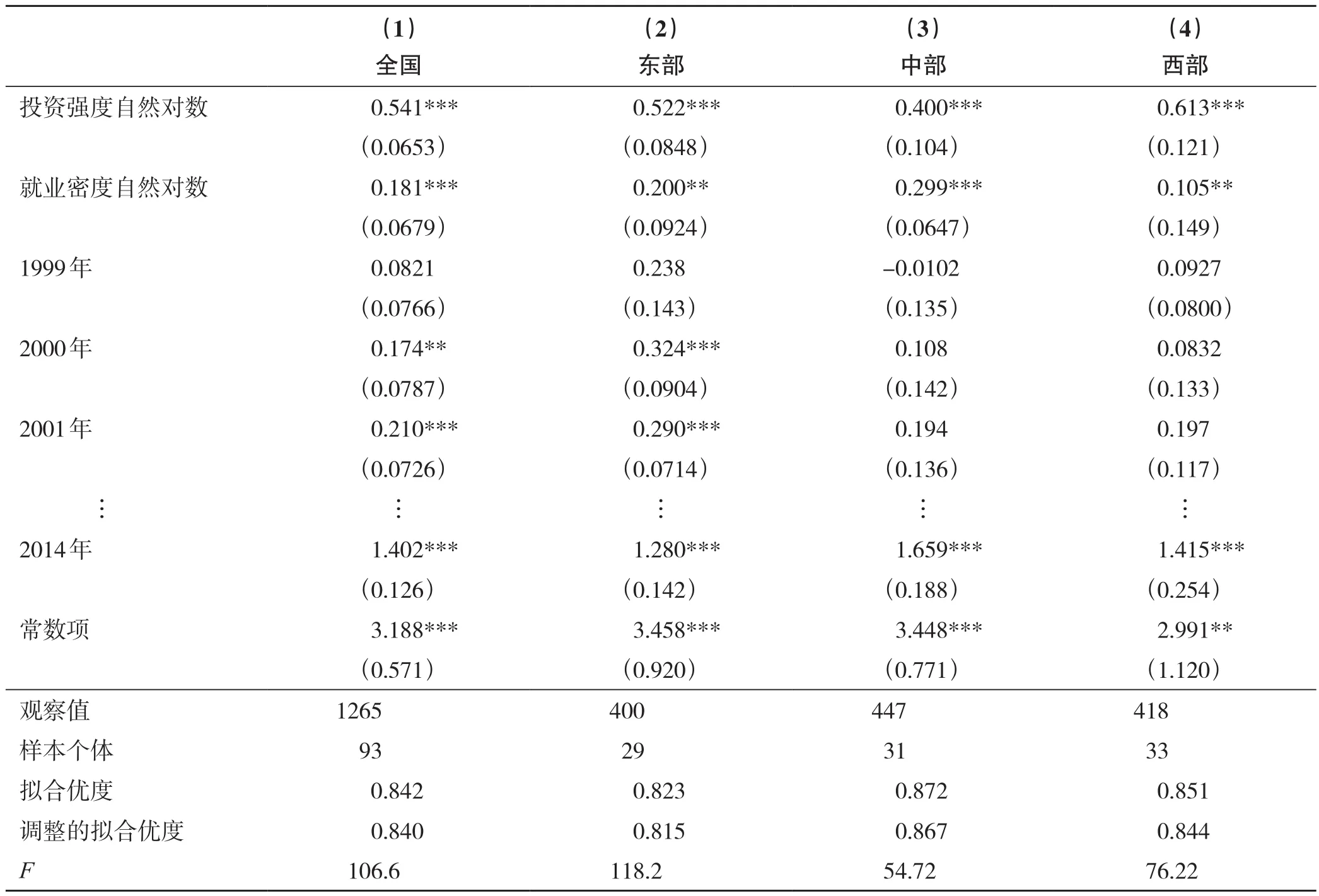
表3 分区域城市工业用地产出率影响因素回归分析与对照Tab.3 Regression and comparison of urban industrial land productivity factors between different areas

表3显示，区域聚类回归分析可以得到统计性质良好的参数，且能够通过经济意义检验，进一步表明双向固定效应模型（式（3））的回归结果是可信的。

5 投资强度、就业密度、TFP对地级城市工业用地产出率的贡献及区域比较

5.1 个体固定效应和时间固定效应的衡量

采用双向LSDV法，对个体特征和时间固定效应都定义虚拟变量，采用稳健标准误，回归模型（式（3））得到与Two-way FE相同的回归参数和高达0.9317的拟合优度，并可同时查看个体固定效应和时间固定效应。对统计显著的个体虚拟变量的参数与常数项相加后取均值，发现城市个体固定效应因地区不同而相异，东部以3.41居高，西部以2.92居末，个体固定效应的全国平均值为3.071；同时发现，时间固定效应逐年递增，其平均值为4.521。

5.2 地级城市工业用地投资强度和就业密度对产出率的边际贡献

将上述个体固定效应、时间固定效应和残差对工业用地产出率的影响合并记为全要素生产率的对数（lnA），并将上述回归参数代入模型（式（3）），经适当变形可得：

进行样本平均，利用式（5）计算不同年份的工业用地投资强度和就业密度对产出率的边际贡献（表4），发现投资强度和就业密度对工业用地产出率的边际贡献逐年递增。在1998年地级城市工业用地投资强度每增加1万元，可使产出率增加0.828万元，到2014年则可增加1.835万元；在1998年就业密度每增加1个单位（104人/km2），可使产出率增加1.315亿元，到2014年则可增加8.662亿元。

表4 工业用地投资强度和就业密度对产出率的边际贡献Tab.4 Marginal productivity contribution of urban industrial land investment intensity and employment density

5.3 分区域地级城市工业用地投资强度、就业密度的边际贡献和全要素生产率

对各区域的比较可以发现，中部和西部地区地级城市工业用地产出率、投资强度和就业密度在绝大多数年份都低于东部地区（图2）。其中，产出率和投资强度低于东部地区通常可理解为“中西部地区资本密集型和技术密集型产业比重更低、劳动密集型产业比重更高”，这意味着更高的就业密度。但是，就业密度的数据比较结果恰恰与此相悖，表明中西部城市工业用地集约利用度和东部相比存在较大的差距。

用分区域聚类回归所得参数替代式（5）的参数，可计算中国东部、中部、西部地区地级城市工业用地的全要素生产率以及投资强度、就业密度的边际贡献（表5）。为增强现势性而分析2010—2014年均值①若考察1998—2014年均值，可以得到类似结果。，发现全要素生产率呈现“东部＞中部＞西部”态势，吻合中国工业总体布局：东部以技术密集型为主，中部由于老工业基地较多而以资本密集型为主，西部则以劳动密集型为主。表5显示西部投资强度边际贡献较高，可能的解释是西部用地粗放，投资强度较低，资本稀缺度较高；西部就业密度边际贡献最低，可能的解释是西部劳动密集型产业工人人力资本较低。中部投资强度边际贡献最低，可能的解释是中部布局了较多技术进步慢的资本密集型工业；中部就业密度边际贡献最高，可能的解释是用地较粗放，就业密度低。东部地区投资强度边际贡献最高，可能的解释是东部以技术密集型产业为主导，全要素生产率最高；东部就业密度边际贡献低于中部，可能的解释是东部工业用地集约度高，就业密度高。

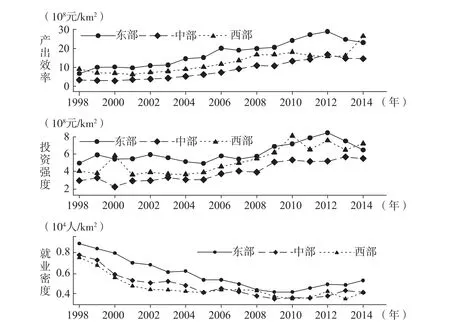
图2 三大区域城市工业用地产出率、投资强度、就业密度变化趋势Fig.2 The change trend of urban industrial land productivity, investment intensity and employment density in the eastern, central and western area

5.4 地级城市工业用地投资强度、就业密度和TFP对产出率提升的贡献率

工业用地产出率的直接影响因素分为投资强度、就业密度和全要素生产率（TFP），其中全要素生产率包括技术进步和残差的影响，技术进步又反映在个体固定效应、时间固定效应之中。借鉴索洛余值法计算全要素生产率（A）的增长率（），存在：

计算式（6）可得1999年以来中国地级城市工业用地投资强度、就业密度和全要素生产率对产出率提升的贡献率。经计算，地级城市工业用地产出率年均增速约为8.7%，投资强度年均增速为3.4%强，就业密度年均下降近3.4%，全要素生产率年均增速约为7.46%。谢花林、王伟等学者[11]发现中国主要经济区城市工业用地TFP在2002—2012年间年均增长8%，笔者的发现与其接近，实现了相互印证。纳入弹性系数因素计算发现，投资强度年均增速带动工业用地产出率年均增长1.86%，贡献率为21.3%；同样方法计算发现就业密度和全要素生产率对1998年来城市工业用地产出率增长的贡献率分别为-7%和85.7%。

6 研究结论和政策建议

工业用地投资强度对产出率的提升作用与人们的预期存在较大的差距，地级城市工业用地投资强度对产出率增长的贡献率只有21.3%。表4显示，由于全要素生产率的积极作用和较慢的工业用地投资强度增速的影响，工业用地投资强度的边际贡献逐年递增，从2014年数据来看，单位工业用地的固定资产每增加1万元，可使产出率增加1.84万元。所以，当前通过遏制工业用地粗放利用、提高工业用地容积率、严格执行工业项目用地投资强度标准、鼓励工业固定资产投资等政策措施适度提高工业用地投资强度是必要的，分区域比较分析则表明对于西部地区尤其需要加强实施工业用地投资强度促进政策。

表5 分区域地级城市工业用地投资强度、就业密度的边际贡献和全要素生产率Tab.5 Marginal contribution of the prefecture level urban industrial land investment intensity and employment density and total factor productivity in different regions

城市工业用地就业密度逐步下降是大势所趋，但存在非正常下降因素，应予以遏制。城市工业用地就业密度对产出率的弹性系数为0.181，但由于工业用地就业密度呈现逐渐下降态势，1999年来对产出率提升的贡献率为-7%。由于技术进步、产业升级、劳动者素质提升等因素影响，长期来看，就业密度必然呈现下降态势。不过，一些非正常因素也可能对就业密度下降做出了贡献，比如工业从业人员待遇过低、生活保障不足、工业用地供地冗余等。5.2节表明，2014年新增1位工业从业人员的边际贡献是8.66万元，与工业从业人员（含管理层和专业技术人员）的年薪均值相近，符合劳动报酬与其边际贡献相等的原则。这表明目前遏制工业就业密度非正常下降的主要着力点不宜放在工资水平调整上。鉴于目前工业园“孤岛”[39]和粗放用地并存的现象，应注重强化各工业园区员工的生活保障，并应采取有力措施遏制各地尤其是中西部工业园区、工业新城建设中出现的盲目铺大摊子行为。

全要素生产率是推进城市工业用地产出效率提升的首要因素，显示工业经济发展方式呈现了积极的转变，应加强其作用以加速这种转变，在工业用地配置和集约性评价中高度重视全要素生产率相关指标，并赋予足够高的权重。TFP包括个体固定效应、时间固定效应和残差的影响，其中，个体固定效应包括区位、自然环境、历史人文环境等变量，时间固定效应包括技术进步、宏观经济变动、产业政策影响等变量。分析显示，无论在统计意义上还是经济意义上，个体固定效应和时间固定效应对工业用地产出效率都存在显著影响。所以，一方面要积极推进技术进步，还要注重改善营商环境、健全基础设施，要缩小中西部与东部地区在这些方面的差距，并要加快中部地区老工业基地转型升级，加速提升全要素生产率。

鉴于数据可得性，本文没有把地均人力资本从就业密度中剥离出来，没有在个体固定效应和时间固定效应之外探讨全要素生产率的来源，有待进一步完善。

（References）：

［1］ 习近平. 在中央城镇化工作会议上的讲话［A］ . 中共中央文献研究室. 十八大以来重要文献选编（上）［M］ . 北京：中央文献出版社，2014：589 - 607.

［2］ 李克强. 凝聚共识、形成合力推进城镇化更稳更好发展［A］ . 中共中央文献研究室. 十八大以来重要文献选编（上）［M］ . 北京：中央文献出版社，2014：608 - 622.

［3］ 曹建海. 中国城市土地高效利用研究［M］ . 北京：经济管理出版社，2002：102 - 104．

［4］ 郑振刚. 供给侧结构性改革下创新存量工业用地管理探析［J］ . 中国土地，2016，（8）：15 - 17.

［5］ 张琳，王亚辉. 微观企业视角下工业用地产出效率的影响因素研究［J］ . 华东经济管理，2014，28（9）：43 - 48.

［6］ 舒帮荣，刘友兆，王家富，等. 欠发达地区经济开发区工业用地低效利用问题初探［J］ . 开发研究，2009，（2）：80 - 83.

［7］ 王成新，刘洪颜，史佳璐，等. 山东省省级以上开发区土地集约利用评价研究［J］ . 中国人口·资源与环境，2014，24（6）：128 -135.

［8］ 陈伟，彭建超，吴群. 城市工业用地利用损失与效率测度［J］ . 中国人口·资源与环境，2015，25（1）：15 - 22.

［9］ Erik Louw, Erwin van der Krabben, Hans van Amsterdam. The Spatial Productivity of Industrial Land［J］ . Regional Studies，2012，46（1）：137 - 147.

［10］ 冯长春，刘思君，李荣威. 我国地级及以上城市工业用地效率评价［J］ . 现代城市研究，2014，（4）：45 - 49.

［11］ 谢花林，王伟，姚冠荣，等. 中国主要经济区城市工业用地效率的时空差异和收敛性分析［J］ . 地理学报，2015，70（8）：1327 -1338.

［12］ 龙开胜，陈利根，占小林. 不同利用类型土地投入产出效率的比较分析［J］ . 中国人口·资源与环境，2008，18（5）：174 - 178.

［13］ 王希睿，许实，吴群，等. 江苏省建设用地利用效率和全要素生产率的时空差异分析［J］ . 中国土地科学，2015， 29（5）：77 - 83.

［14］ 张琳，王亚辉，李影. 全要素生产率视角下的城市工业用地生产效率研究［J］ . 大连理工大学学报（社会科学版），2015，36（1）：57 - 62.

［15］ Tu Fan, Yu Xiaofen, Ruan Jianqing. Industrial land use efficiency under government intervention: Evidence from Hangzhou, China［J］ . Habitat International，2014，43（7）：1 - 10.

［16］ 赵爱栋，马贤磊，曲福田. 市场化改革能提高中国工业用地利用效率吗？［J］ . 中国人口·资源与环境，2016，26（3）：118 - 126.

［17］ Du J. Urban land market and land-use changes in post-reform China: A case study of Beijing［J］ . Landscape and Urban Planning，2014，124：118 - 128．

［18］ Gao By, Li Wd. State land policy, land markets and geographies of manufacturing: The case of Beijing，China［J］ . Land Use Policy，2014，36：1 - 12.

［19］ 郭贯成，温其玉. 环境约束下工业用地生产效率研究［J］ . 中国人口·资源与环境，2014，24（6）：121 - 126.

［20］ 陈逸，黄贤金，陈志刚，等. 城市化进程中的开发区土地集约利用研究［J］ . 中国土地科学，2008，22（6）：11 - 16.

［21］ 罗能生，彭郁. 中国城市工业用地利用效率时空差异及地方政府竞争影响［J］ . 中国土地科学，2016，30（5）：62 - 71.

［22］ 孟媛，张凤荣，赵婷婷，等. 北京市顺义区制造业用地集约度评价及影响因素分析［J］ . 中国土地科学，2011，25（2）：11 - 17.

［23］ 林坚，张沛，刘诗毅，等. 基于生产函数的工业用地级差收益研究［J］ . 城市发展研究，2010，17（6）：80 - 85.

［24］ Robert M. Solow. Technical change and the aggregate production function［J］ . the Review of Economics and Statistics，1957，39（3）：312 - 320.

［25］ John W. Kendrick, Ryuzo Sato. Factor prices, productivity, and economic growth［J］ . The American Economic Review，1963，53（5）：974 - 1003.

［26］ 周方. 科技进步与“增长函数”［J］ . 数量经济技术经济研究，1999，（10）：32 - 50.

［27］ 谭崇台. 发展经济学［M］ . 太原：山西经济出版社，2001：113.

［28］ 林荣茂，刘学敏. 中国工业用地利用的数理分析与实证研究［J］ . 财经研究，2008，34（7）：51 - 62.

［29］ 杨杨，吴次芳，韦仕川，等. 土地资源对中国经济的“增长阻尼”研究——基于改进的二级CES生产函数［J］ . 中国土地科学，2010，24（5）：19 - 25.

［30］ 王克强，熊振兴，高魏. 工业用地使用权交易方式与开发区企业土地要素产出弹性研究［J］ . 中国土地科学，2013，27（8）：4 - 9.

［31］ 李谷成. 资本深化、人地比例与中国农业生产率增长——一个生产函数分析框架［J］ . 中国农村经济，2015，（1）：14 - 31.

［32］ Antonio Ciccone, Robert E. Hall. Productivity and the density of economic activity［J］ . The American Economic Review，1996，86（1）：54 - 71.

［33］ 黄大全，洪丽璇，梁进社. 福建省工业用地效率分析与集约利用评价［J］ . 地理学报，2009，64（4）：479 - 486.

［34］ 郭贯成，熊强. 城市工业用地效率区域差异及影响因素研究［J］ . 中国土地科学，2014，28（4）：45 - 52.

［35］ 毕宝德，柴强，李铃，等. 土地经济学（第六版）［M］ . 北京：中国人民大学出版社，2011：8.

［36］ 李子奈，叶阿忠. 高级应用计量经济学［M］ . 北京：清华大学出版社，2012：10.

［37］ 靳云汇，金赛男.高级计量经济学（下册）［M］ . 北京：北京大学出版社，2011：179.

［38］ 陈强.高级计量经济学及Stata应用（第二版）［M］ . 北京：高等教育出版社，2013：251.

［39］ 王慧. 开发区与城市相互关系的内在机理及空间效应［J］ . 城市规划，2003，27（3）：20 - 25.

（本文责编：陈美景）

The Impact Factors of Urban Industrial Land Productivity and Comparison among Different Regions: A Panel Data Analysis of Prefecture-level Cities

XU Ming-qiang1，2
（1. School of Tourism and Economic Management, Chengdu University, Chengdu 610106, China; 2. Postdoctoral Mobile station of Applied Economics，Southwestern University of Finance and Economics, Chengdu 610074, China）

The purpose of the research is to find out the impact factors, impact degrees and regional differences of urban industrial land productivity, and to come up with relevant recommendations to impel the intensive use of urban industrial land. Based on the relatively extensive use of urban industrial land and the lack of empirical research regarding the impact factors of urban industrial land productivity in China, the Cobb-Douglas production function is improved according to the land function theory and the two-way fixed effects panel data model of urban industrial land productivity is established, which takes the urban industrial land capital intensity and its employment density as the core explanatory variables. Empirical research on the data of 93 prefecture-level cities since 1998 shows that the coefficient ofelasticity of urban industrial land capital intensity and the employment density towards its productivity are 0.541、0.181 respectively. Besides, the total factor productivity is the most influential factor towards industrial land productivity, and the contribution rate of these three factors to the growth of urban industrial land productivity since 1998 was 21.3% and -7% and 85.7% respectively. And the marginal contribution rates in terms of urban industrial land productivity present regional differences due to the intensity of industrial land, industrial types and labor quality in the eastern, central and western area. In conclusion, the extensive use of land is supposed to be curbed especially in the construction of the new industrial zone in central and western areas , and industrial investment should be promoted in order to increase capital intensity and employment density; indicators that reflect the total factor productivity should be brought into the allocation and evaluation of urban industrial land; the gap between the eastern and the central and western regions in the business environment, infrastructure and other areas should be narrowed.

land use; total factor productivity; two-way fixed effects; industrial land productivity; capital intensity; employment density

F293.2

A

1001-8158（2016）12-0071-12

10.11994/zgtdkx.20161217.013049

2016-08-14；

2016-10-31

教育部人文社科规划基金项目“产城融合关键因素和影响机制研究”（15YJA790074）；中国博士后科学基金资助项目“基于中外工业园经验数据的产城融合实现机制实证研究”（2015M572487）。

许明强（1975-），男，四川安岳人，博士，副教授。主要研究方向为城镇化与工业化。E-mail: thinker127@qq.com