土地利用变化驱动力多尺度因素的定量影响分析

袁 磊，杨 昆

（1.云南师范大学信息学院，云南 昆明 650500；2.西部资源环境地理信息技术教育部工程研究中心，云南 昆明 650500）

土地利用变化驱动力多尺度因素的定量影响分析

袁 磊1，2，杨 昆1，2

（1.云南师范大学信息学院，云南 昆明 650500；2.西部资源环境地理信息技术教育部工程研究中心，云南 昆明 650500）

研究目的：揭示多尺度土地利用变化研究中尺度因素对驱动力的定量影响。研究方法：构建Logistic回归模型和二分类反应变量两水平Logistic回归模型，分别基于面向尺度对比的多尺度回归分析和基于系统观点的多水平模型分析两个角度，探讨多尺度土地利用变化核心驱动力及其定量影响关系，并对两类模型的分析结果进行对比分析。研究结果：面向尺度对比的多尺度回归分析法能够从更为微观的角度揭示各个尺度层级上地类变化的核心驱动因子，而基于系统观点的多水平模型分析方法则能够更好地顾及尺度因素的定量影响。研究结论：多水平模型分析方法揭示的各个地类的核心驱动因子集与多尺度回归分析法推导的对应地类的核心驱动因子集之间呈现子集关系，两者在多尺度土地利用变化驱动力的研究方法上能够形成互补。

土地利用；多尺度；驱动力；多水平模型；Logistic回归模型

土地利用变化驱动力是导致土地利用方式和目的发生变化的各种社会经济因素和生物物理因素的总称[1]。土地系统的驱动力多尺度问题已成为土地科学领域创新性探索的重要研究方向之一[2]，研究主要集中在土地利用变化动力的多尺度模拟[3]、空间自相关性[4]、尺度依赖性规律[5-6]及空间尺度效应[7-10]等方面。 由于尺度问题本身的复杂性，加之各类方法或重于数量关系的分析，或偏于空间关系的表达，使得目前已有研究通常只能提供多尺度土地利用系统的部分信息。本文立足于多尺度研究视角，以建设用地变化自然因素驱动力为研究对象，首先从多尺度回归分析的角度，分析不同尺度建设用地变化的驱动机理，寻求建设用地变化多尺度核心驱动因子；其次，从系统整体的角度，将多水平模型理论与方法引入土地利用变化驱动力多尺度研究中，将尺度作为一个独立的定量因素加入模型，构建土地利用变化空间多尺度驱动力二分类反应变量两水平Logistic回归模型，探讨多尺度建设用地变化的核心驱动力；最后，将上述两种不同方法得到的核心驱动因子集进行对比分析，揭示多尺度土地利用变化研究中尺度因素对驱动力的定量影响，以期弄清多尺度层级间引起土地利用变化的作用机制，为引导土地资源在不同尺度层级间的时空优化配置提供参考。

1 研究区概况及数据来源

本文选择中国西南典型高原山区—云南省、昆明市、宜良县组成3级实证研究区。该研究区地处中国西南边陲，云贵高原西南部，位于东经97°31′39″—106°11′47″、北纬21°8′32″—29°15′8″之间，西部为横断山脉高山峡谷区，东部属云贵高原区，南部为中、低山宽谷盆地区，全区以高原山地为主。研究期内，一批支柱产业与特色产业得到培育，社会经济发展迅速，建设用地格局变化显著，具有一定的代表性。实证研究中采用云南省、昆明市、宜良县1999—2008年的土地利用及自然地理数据，主要包括：土地利用现状数据、土地利用变更数据、交通分布矢量数据、水系分布矢量数据，由等高线生成的DEM及派生的地形图、坡度图、坡向图等。

2 研究方法

2.1 驱动因子选取

自然因素驱动力主要决定土地利用/覆盖变化的空间格局，是影响区域土地利用变化的基础背景因素。由于研究区地处中国西部高原山区，地形高差大、切割剧烈，地学因子存在着显著的空间分异。这些分异较大的地学因子便成为了研究区区别与其他区域，并影响其土地利用/覆盖空间格局变化的基础因素，也是驱动因子选取时重点考虑的对象。因此，本文首先根据研究区地学因子时空分布的特点，并考虑因子数据的可获取性、因子本身的代表性及与相应尺度上建设用地变化的相关性进行综合选取；在此基础上，进一步采用特尔菲法给出各因子相对重要性的定量表示，最终经过多轮打分筛选，确定了两大类9项自然因素驱动因子，形成本文的驱动因子指标体系，开展土地利用变化驱动力多尺度定量关系对比研究（表1）。

2.2 数据处理

2.2.1 因变量因子数据处理 因变量因子即地类因子。基于研究期各尺度土地利用变化矢量图层，利用ArcGIS平台空间数据处理功能，分别建立居民点及独立工矿用地、交通水利设施用地对应的属性字段，通过空间属性查询（Select by Attribute）及字段计算（Field Calculator），按地类的空间分布情况对各属性字段分别赋值。最终形成一个具有二分性属性的土地利用变化图层。二分性的定性变量只有“1”或“0”两个值，即“是”与“否”，从而分别对每一地类是否发生变化进行空间标识。

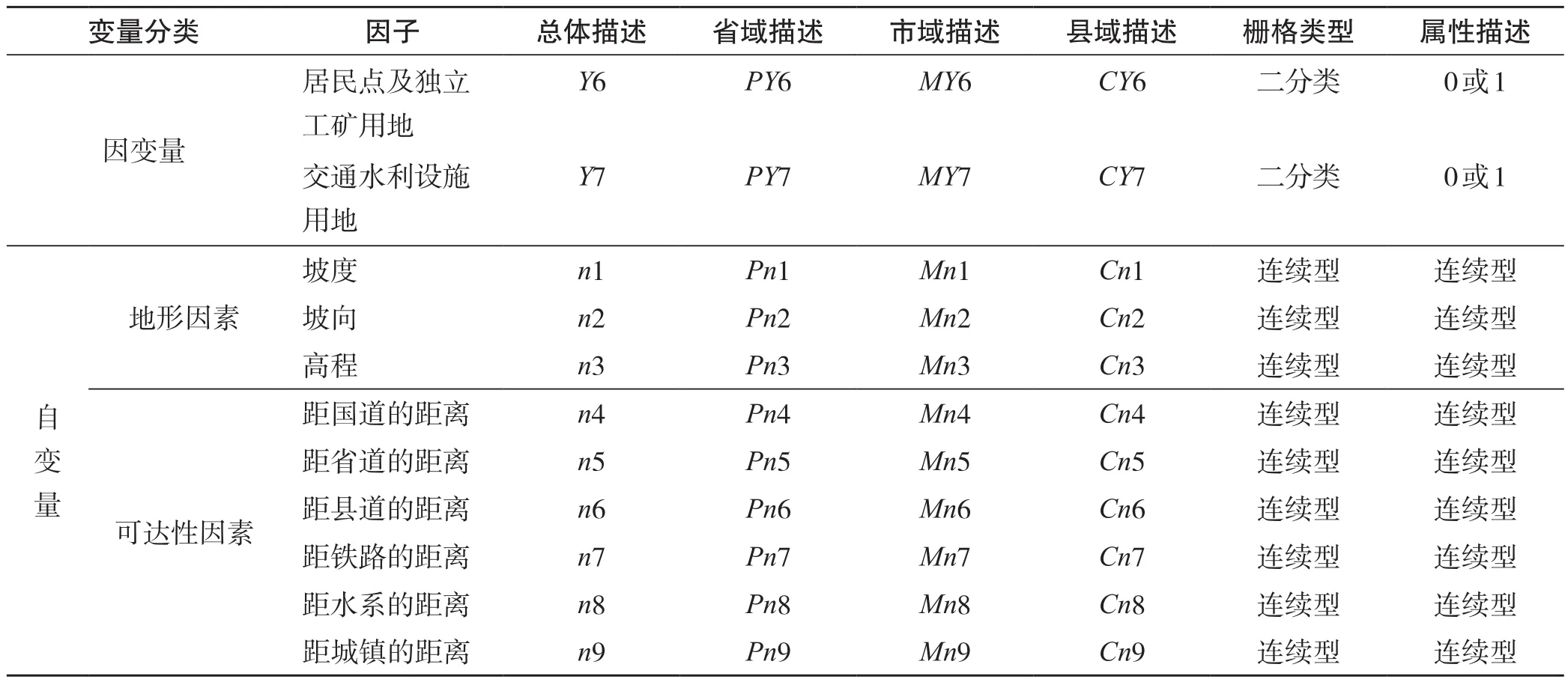
表1 多尺度研究区建设用地变化驱动因子指标体系及其描述Tab.1 Index system and description of driving factors for construction land change in multi-scale study area

2.2.2 自变量因子数据处理 自变量因子即自然因素驱动力因子。对于自变量因子的数据获取，例如，高程因子基于研究区等高线，在ArcGIS平台中生成数字高程模型（DEM）得到；坡度、坡向因子是基于生成的DEM，采用地形因子提取 “slope”和“aspect” 功能进一步提取得到；距国道、省道、县道、铁路、水系的距离等驱动因子，利用各自对应的线状要素，根据研究需要分别设置相应的缓冲半径，进行多级缓冲区分析得到；距城镇的距离等点状要素驱动因子通过对城镇等点层要素进行同样的多级缓冲区分析，并由分别生成的相应驱动因子图得到。

2.3 驱动力多尺度回归分析模型

本文采用Logistic逐步回归分析法对建设用地变化多尺度驱动力进行定量分析。Logistic回归模型不需要假设变量之间存在多元正态分布，采用最大似然估计法进行参数估计，以事件发生概率的形式提供结果。借助该模型能对二值响应的因变量和分类变量（连续型或混合型）进行回归建模，进而探讨影响概率及主要的影响因子。

根据Logistic回归建模要求，本文设X1，X2，……是与Y相关的一组向量，设P是某事件发生的概率，将比数P/（1-P）取对数得到ln［P/（1 - P）］，即对P作Logistic变换，记为Logit（P），回归模型如下：

式（1）中， Pi是给定系列自变量xi的值时事件的发生概率，a为截距，β为Logistic回归的偏回归系数，表示变量xi对记为Logit（P）的影响大小。

发生事件的概率是一个由自变量xi构成的非线性函数，表达式如下：

本文采用SPSS 20逐步回归分析的Logistic函数完成多尺度自然因素驱动力的分析。所得到的Logistic回归分析结果包括回归系数、回归系数估计的Waldx2统计量、回归系数估计的标准差、回归系数估计的显著性水平。其中，Waldx2统计量表示每个（解释变量）在模型中的相对权重，用来评价每个解释变量对事件预测的贡献力。

对于模型拟合优度的检验，本文采用Homsmer Lemeshow（HL）指标。当前，用于拟合优度检验的指标有HL指标、偏差D、皮尔逊等，但当模型中存在连续型自变量时，偏差D及皮尔逊检验方法将不再适用，而在使用包含连续型自变量的Logistic回归分析模型，HL是广为接受的模型拟合优度的检验指标[11]。当HL指标统计不显著时，表示模型拟合较好；相反，如果HL指标统计显著，则说明模型拟合不好。HL指标计算公式如下：式（3）中，K表示分组数，ni表示第i组中的案例数，yi表示第i组事件的观测数据量表示第i组预测事件概率，nii表示事件预测数。

2.4 驱动力多尺度多水平模型

2.4.1 模型研究现状与特征分析 多水平模型最早由Lindley和Smith于1972年提出，直到1998年，英国伦敦大学教育研究所Goldstein博士出版专著《Multilevel Statistical Models》，多水平模型理论与方法才趋于完善[12]。多水平模型考虑了数据间的层次性，可以将传统模型中的随机误差项分解到与数据层次结构相对应的水平上，使得个体的随机误差更纯，并可将各水平残差拟合成某些变量的函数，从而为分析个体变化趋势及其影响因素提供可能。该模型正是针对这种具有层次结构特征的数据而发展起来的一种专门用于处理非独立性数据的多元统计分析方法。目前，该模型在医学[13]、气象学[14]、社会学[15]等领域已有成功的应用案例，而在土地科学领域应用较少。国外，hoshino通过区分市级和省级数据，采用多水平模型对日本土地利用结构和变化进行了分析[16]；Polsky和Easterling运用类似方法分析了美国大湖平原的土地利用结构和等级特征[17]；Verburgb在对菲律宾土地利用研究中讨论了多水平建模对土地用途研究和数据收集的影响[18]；国内，蔡运龙教授指出可以利用多水平统计学分析土地变化格局、过程及其驱动力和效应中的“连通性”问题[19]。

就本文而言，因为研究区界定于有机互联的云南省、昆明市及下辖的宜良县组成的多尺度研究区，在行政尺度上具备自然的隶属关系，数据上不仅包括不同空间尺度、不同时序尺度的土地利用数据，而且，每一空间尺度下、不同时序尺度的土地利用变化本身又受到不同时空尺度的自然因素的驱动。按照层次理论的观点，这种多尺度性表征的就是一种层次结构。因此，不同尺度、不同时序的土地利用变化及其对应的驱动因素数据序列就是一个具有层次结构的多级数据序列，适宜采用多水平模型理论与方法开展研究。

2.4.2 模型构建 鉴于多水平模型处理多层数据或多级数据方面的优势，本文将多水平模型引入土地利用驱动力多尺度问题的研究方面，针对前述建立的各尺度具有二分性属性数据，此处，将居民点及独立工矿用地、交通水利设施用地两大地类的地类标识变量设为第1水平单位i，省、市、县三级行政尺度的尺度标识变量设为第2水平单位j，构建多尺度地类变化及其自然因素驱动因子之间的二分类反应变量两水平Logistic回归模型：

式（4）中，pij表示地类发生变化的比数（率），β1为固定效应参数，μ0j为第2水平单位残差（随机效应），即第2水平单位logit均值β0j与总均值β0之差，σ2μ0是随机参数，反映了高水平单位间的比数的差别，其值越大，说明数据在高水平单位内的聚集性越强，nij为比数（率）的分母，πij（1-πij）/nij表示反应变量的方差估计值。

3 结果分析

3.1 多尺度回归结果分析

按照前述驱动力多尺度回归分析思路与方法，省、市、县不同尺度建设用地变化与其自然因素驱动因子数据开展Logistic逐步回归分析，结果分别如表2—表4所示。

表2 省域尺度自然因素驱动因子对地类变化影响参数Tab.2 Impact parameters of natural driving factors on land use change in provincial scale

表3 市域尺度自然因素驱动因子对地类变化的影响参数Tab.3 Impact parameters of natural driving factors on land use change in municipal scale

表4 县域尺度自然因素驱动因子对地类变化的影响参数Tab.4 Impact parameters of natural driving factors on land use change in county scale

基于上述各尺度层级的建设用地变化与自然因素驱动因子的Logistic逐步回归分析可知：省域尺度上，影响居民点及独立工矿用地变化的核心驱动因子依次是距县道的距离（1.042）、距铁路的距离（0.961）和坡度（0.879）；距县道的距离每增加1 km，发生率将提高4.19%；距铁路的距离每增加1 km，发生率则降低3.92%；坡度每增加1度，发生下降12.10%。交通水利设施用地变化则受坡度（1.422）、距铁路的距离（0.936）、距国道的距离（0.872）、距县道的距离（0.850）、距省道的距离（0.813）及水系（0.478）驱动因素的影响显著。

市域尺度上，居民点及独立工矿用地变化受多种因素的共同影响。依据EXP（B）值的大小，其核心驱动因子依次是距国道的距离（1.032）、距省道的距离（1.023）、高程（1.002）、坡向（0.990）、距城镇的距离（0.988）、坡度（0.913）和距铁路的距离（0.818）。交通水利设施用地变化主要受距城镇的距离（1.032）、距省道的距离（0.950）、距国道的距离（0.941）、距铁路的距离（0.899）的影响较为显著。

县域尺度上，居民点及独立工矿用地主要受距县道的距离（1.354）、距省道的距离（1.163）、距国道的距离（1.084）和坡度（0.782）影响较大。交通水利设施用地变化主要受高程（0.996）、距铁路的距离（0.837）、距省道的距离（0.793）、距国道的距离（0.787）和距水系的距离（0.385）的影响较为显著。

3.2 多水平模型结果分析

基于前述构建的多尺度地类变化及其自然因素驱动因子之间的二分类反应变量两水平Logistic回归模型，首先，以居民点及独立工矿用地标识为水平1单位，以尺度标识作为水平2单位，拟合不含任何驱动因子的二分类反应变量两水平Logistic回归空模型（null model）；其次，考察空模型拟合结果，只有当居民点及独立工矿用地对应的随机截距方差（Intercept）在0.01或0.05水平上显著时，才表明该地类变化在不同尺度间存在差异，才有必要进一步引入协变量（驱动因素）进行多水平分析。对于交通水利设施用地的多尺度拟合同上。最终结果如表5、表6所示。

表5 自然因素驱动因子两水平Logistic回归空模型分析结果Tab.5 Results of two level Logistic regression null model for natural driving factors

由表5可知，就居民点及独立工矿用地而言，其水平2随机系数方差估计值为5.225（P = 0.018），在0.05水平上具有统计学意义，表明居民点及独立工矿用地变化在尺度层级间确实存在一定的差异。因此，需要引入解释变量（核心驱动因子）来进一步分析引起差异的原因。这里，依次将选取的自然因素驱动因子引入模型，重新进行模型拟合，结果发现坡度（n1）、距国道的距离（n4）具有统计学意义，固定效应估计值分别为1.798（P = 0.020）、3.517（P = 0.041），表明尺度层级上坡度、距国道的距离对居民点及独立工矿用地变化的影响较大，见表6所示。

同样，交通水利用设施用地空模型拟合结果发现，水平2随机系数方差估计值为0.019（P = 0.031），具有统计学意义，说明交通水利设施用地变化在尺度层级间也存在差异。因此，也需要引入解释变量做进一步分析。将三级尺度上自然因素驱动因子也逐一引入模型重新拟合，结果如表6所示，距国道的距离（n4）、距省道的距离（n5）、距铁路的距离（n7）具有统计学意义，固定效应估计值分别为1.119（P = 0.026）、0.846（P = 0.001）、2.648（P = 0.001），表明在多尺度层级上距国道的距离、距省道的距离、距铁路的距离对交通水利设施用地变化的影响较为显著，是引起该地类变化的核心驱动因子。

表6 自然因素驱动因子两水平Logistic回归模型参数估计结果Tab.6 Results of parameters estimation of two level Logistic regression model for natural driving factors

3.3 综合对比分析

综合上述多尺度回归分析结果和多水平模型分析结果发现：坡度（n1）对各尺度层级上居民点及独立工矿用地变化具有普遍的驱动意义，距国道的距离（n4）、距省道的距离（n5）对市级和县级尺度上的居民点及独立工矿用地变化具有普遍的驱动意义；而距国道的距离（n4）、距省道的距离（n5）、距铁路的距离（n7）对各尺度层级上交通水利用设施用地也具有普遍驱动意义，即对各个尺度上的交通水利设施用地的变化都表现出了一定的驱动作用，是每一尺度上该地类变化的核心驱动因子。同时，进一步对比分析发现：当将尺度作为一个独立的定量因素加入二分类反应变量两水平Logistic回归模型时，个别在单一尺度中对地类变化具有驱动意义的因子，在尺度定量的多水平模型分析中不再表现出对该地类的驱动作用。例如：就交通水利设施用地而言，在单一尺度的回归分析中，三级尺度总体上影响该地类变化的核心驱动因子集为{n1，n4，n5，n6，n7，n8，n9}，而多水平模型分析交通水利设施用地的核心驱动因子集是{n4，n5，n7}。总体上，多水平模型分析的各个地类的核心驱动因子集与单一尺度回归分析的相应地类的驱动因子集之间呈现子集关系（表7）。

表7 多尺度土地利用变化核心驱动因子列表Tab.7 A list of core driving factors for multi scale land use change

4 结论与讨论

（1）方法上，基于Logistic多元回归分析将驱动因子分解定位到不同的空间尺度，能够从更为微观的角度揭示各个尺度层级上地类变化受驱动因子影响的定量关系。但这种经典数理分析方法实质是将尺度作为一个定性因素，在得到各尺度层级上各地类变化与驱动因子定量影响关系之后，通过尺度之间的直接对比来揭示多尺度土地利用变化驱动力及尺度依赖规律。因此，它没有顾及因尺度因素带来的数据层次结构的存在，忽略了尺度因素在多尺度驱动力分析中的定量影响。而将多尺度土地利用变化及其驱动因素看成一个整体系统，把尺度因素作为独立的控制变量加入模型，从系统整体的角度构建二分类反应变量两水平Logistic回归模型，考虑了尺度因素的定量影响，弥补了驱动力多尺度直接对比分析的不足，从而在方法上与其形成互补研究。

（2）结果上，通过将两种不同方法的研究结果进行对比分析发现，基于Logistic多元回归分析能够更加具体细微地寻求不同尺度上各个地类的核心驱动因子及其定量影响关系；而二分类反应变量两水平Logistic回归模型则是从系统整体角度揭示多尺度土地利用变化及其驱动力系统中引起各个地类发生变化的公共核心驱动因子及其定量影响程度。总体上，多水平模型分析得到的各个地类的核心驱动因子集与单一尺度回归分析得到的相应地类的驱动因子集之间呈现子集关系。

由于土地利用变化本身是一个受特定区域经济、社会、自然和政策倾向等综合因素影响的复杂过程，而本文从多尺度视角对其进行审视，无疑更加剧了这一问题的复杂程度，而且本文仅考虑自然因素的驱动作用，一定程度上影响了分析结果的客观性；此外，将多水平模型引入土地利用变化多尺度驱动力问题的研究之中也是一次新的尝试，研究数据也仅是连续10年期数据，这也使得该模型的优势尚没有充分体现。因此，下一步工作应从宏观、中观、微观更多尺度层级、更多时点上收集数据，进一步丰富多尺度样本数据，可进一步深入探讨在尺度因素定量影响下驱动因子对不同尺度土地利用变化的驱动效应及跨尺度交互作用的性质和程度。

（References）:

［1］ 杨梅，张广录，侯永平. 区域土地利用变化驱动力研究进展与展望［J］ . 地理与地理信息科学，2011，27（1）： 95 - 100.

［2］ 赵俊三，袁磊，张萌. 土地利用变化空间多尺度驱动力耦合模型构建［J］ . 中国土地科学，2015，29（6）：57 - 66.

［3］ Verburg P. H., Veldkamp A. Fresco L. O. Multi-scale modeling of land-use change dynamics in Ecuador［J］ . Agricultural Systems，1999，61（2）：77 - 93.

［4］ Overmars K. P., Koning G. H. J. de, Veldkamp A. Spatial autocorrelation in multi-scale land use models［J］ . Ecological Modelling，2003，164（2-3）：257 - 270.

［5］ Viglizzo E. F., Pordomingo A. J., Castro M. G., et al. Scale-dependent controls on ecological functions in agroecosystems of Argentina［J］ . Agriculture, Ecosystems & Environment，2004，101（1）：39 - 51.

［6］ 邱炳文. 福建省耕地多尺度空间分布特征分析［J］ . 农业工程学报，2008，24（11）：63 - 68.

［7］ Batisani N., Yarnal B. Urban expansion in Centre County, Pennsylvania: Spatial dynamics and landscape transformations［J］ . Applied Geography，2009，29（2）：235 - 249.

［8］ Pan Y., Roth A., Yu Z., et al. The impact of variation in scale on the behavior of a cellular automata used for land use change modeling［J］ . Computers, Environment and Urban Systems，2010，34（5）：400 - 408.

［9］ 王天巍，李朝霞，史志华，等. 都市圈边缘区多尺度土地利用驱动力研究［J］ . 华中农业大学学报，2008，27（4）：471 - 477.

［10］ 蒙吉军，朱利凯，毛熙彦. 近30年来毛乌素沙地土地利用变化驱动力的多尺度研究——以内蒙古乌审旗为例［J］ . 应用基础与工程科学学报，2012，20（Z1）：54 - 66.

［11］ Morgan S, Philip, Jay D. Teachman. Logistic regression: Description, examples, and comparisons［J］ . Journal of Marriage and the Family，1988，50：925 - 936.

［12］ Goldstein H. Multilevel Statistical Models［M］ . New York: Oxford University Press Inc，1999.

［13］ 马修强. 多水平模型和关联规则联合研究胃食管反流病影响因素［D］ . 上海：第二军医大学，2009.

［14］ 郑文波. 基于多水平统计模型的气象数据研究［D］ . 武汉：华中科技大学，2010.

［15］ 韩军辉. 中国农村地区代际收入流动的多水平统计模型分析［J］ . 统计与信息论坛，2009，24（8）：17 - 20，33.

［16］ Hoshino S. Multilevel modeling on farmland distribution in Japan［J］ . Land Use Policy，2001，18：75 - 90.

［17］ Polsky C, Easterling IIIW E. Ricardian climate sensitivities: accounting for adaptation across scales［J］ . Agriculture, Ecosystems and Environment，2001，85：133 - 144.

［18］ Peter H. Verburgb. Multilevel modeling of land use from field to village level in the Philippines［J］ . Agricultural Systems，2006，89（2 - 3）：435 - 456.

［19］ 蔡运龙. 贵州喀斯特高原土地系统变化空间尺度综合的一个研究方案［J］ . 地球科学进展，2009，24（12）：1301 - 1308.

（本文责编：王庆日）

An Analysis of Quantitative Impacts of Multi-scale Factors on Driving Forces in Land Use Change

YUAN Lei1，2, YANG Kun1，2
（1. School of Information Science and Technology, Yunnan Normal University, Kunming 650500, China; 2. Engineering Research Center of Ministry of Education on Geography Information Technology of Western Resource Environment, Kunming 650500, China）

The purpose of this study is to reveal quantitative impacts of multi-scale factors on driving forces in multiscale land use change. Firstly, Logistic Regression Model and Two Level Logistic Regression Model of two category response variable are constructed. Secondly, the core driving forces of multi-scale land use change and relationship among them and their quantitative effects are discussed and compared from the two perspectives i.e., one is comparison of multi-scale, the other is systematic viewpoint. The results of the study show that the method of Logistic Regression Model can be used to reveal quantitative relationship among driving factors and land use change in different scale levels, and the method of Two Level Logistic Regression Model of two category response variable has taken quantitative effects of scale factors into consideration. It is concluded that the sub-assembly of core driving factors revealed by the multi-levelmodel is included in the sub-assembly explored by multi-scale model, and the two methods can also form complementary research on core driving forces of multi-scale land use change.

land use; multi-scale; driving forces; multilevel model; Logistic regression model

F301.24

A

1001-8158（2016）12-0063-08

10.11994/zgtdkx.20161219.132637

2016-06-21；

2016-09-18

云南师范大学博士科研启动项目（01000205020503063）；国家科技支撑计划项目（2013BAJ07B00）。

袁磊（1977-），男，河南潢川人，博士，硕士生导师。主要研究方向为GIS理论与应用，自然资源配置与规划。E-mail: v_ict@163.com

杨昆（1963-），男，云南昆明人，博士生导师，教授。主要研究方向为时空过程模拟，GIS理论。E-mail: kmdcynu@163.com