水电厂突发事件应急能力的二元语义度量模型

郑霞忠，邵 波，陈 玲，胡宇峰，陈 述

(1.三峡大学水利与环境学院,湖北 宜昌 443002；2.三峡地区地质灾害与生态环境湖北省协同创新中心,湖北 宜昌 443002)

近些年，水电厂单机容量和装机规模越来越大，自动化程度越来越高[1]，然而受诸多不安全因素影响，水电厂电力生产突发事件时有发生，且危害程度大。同时，水电厂运行管理人员呈现精简化、年轻化趋势，工作经验和突发事故处理经验不足[2]，加之水电厂地理位置特殊，大部分厂址位于高山峡谷之中，交通不便，突发事件处理困难[3]；一旦发生事故，若没有及时有效地应急救援，轻则影响水电厂生产设备正常运转，重则致使人员伤亡或电网大范围停电，更可能造成电网瓦解等灾难性后果。因此，开展水电厂突发事件应急能力度量研究对提高水电厂运行人员突发事件处理能力、保障水电厂安全高效运行具有重要意义。

目前，众多学者开展关于如何应对水电厂突发事件的研究，提出了相应的水电厂突发事件应对措施和建议[4,5]，但大多针对具体的突发事件或是宏观上的统筹，缺乏系统地分析水电厂突发事件应急能力，同时也较少考虑影响水电厂突发事件应急能力因素之间的内在联系。鉴于此，本文从安全系统学理论出发，建立科学全面的水电厂突发事件应急能力评价指标体系，构建水电厂突发事件应急能力的二元语义度量模型，旨在科学系统地刻画水电厂突发事件应急能力，以期为提高水电厂突发事件应急能力提供理论依据。

1 指标体系

水电厂突发事件应急能力度量是一个涉及众多环节和诸多因素的复杂系统工作，为了客观真实地刻画水电厂突发事件应急能力，根据国家有关法律法规、水电厂突发事件应急管理程序及其应急能力特性，结合水电厂运行管理专家建议，从多层次和多角度加以考虑和设计，综合考虑各因素间的科学性、独立性、可操作性，建立了包括预防与应急准备、应急监测与预警、应急处置与救援和应急恢复与重建等4个一级指标及17个二级指标的水电厂突发事件应急能力指标体系。指标体系由目标层、准则层和子准则层(指标层)三部分组成，其递阶层次结构见图1。

图1 水电厂突发事件应急能力评价指标体系Fig.1 Evaluation index system of hydropower emergency response capacity

2 应急能力的二元语义度量模型

2.1 二元语义及其集结算子

二元语义是一种基于符号转移概念、采用二元组(sk,αk)表示专家语言评价信息的方法[6]，其中sk为预先定义好的语言评价集S中的语言短语，αk称为符号转移值，表示评价结果与sk的偏差，且满足αk∈[-0.5,0.5)。

语言评价集S是一个预先定义好的由奇数个语言短语构成的有序集合，即S={sk|k=0,1,…,g}，g+1为语言评价集中元素的个数，其中语言短语sk可以通过转换函数θ得到相应的二元语义形式：

θ:S→S×[-0.5,0.5)

θ(sk)=(sk,0),sk∈S

(1)

设β∈[0,g]为语言评价短语集结运算的数值结果，则可由函数Δ得到与之相对应的二元语义形式：

(2)

式中：round为取整函数。

同时，存在一个逆函数Δ-1使二元语义(sk,αk)转化为相应的数值β∈[0,g]：

Δ-1:S×[-0.5,0.5)→[0,g]

Δ-1(sk,αk)=k+αk=β

(3)

若ST={(s1,α1),(s2,α2),…,(sT,αT)}为一组二元语义，W=(w1,w2,…,wT)是与之对应的权重向量，则二元语义的加权算术平均算子

(4)

2.2 指标赋权

指标权重的确定客观与否直接关系到度量结果的优劣。由于度量信息的不完备和专家经验判断的模糊性，水电厂突发事件应急能力度量具有很大的模糊性；在评价指标重要性的两两比较中，若采用传统AHP方法往往会出现不太确定或不太合适的主观判断，若采用区间数来描述评价指标相对重要性，能够充分考虑应急能力度量的模糊性，大大减少人为主观判断的影响[7]。因此，本文采用区间层次分析法(IAHP)确定评价指标权重，以期尽可能得到客观合理的指标权重。具体步骤如下：

(1)形成区间判断矩阵。参照指标体系层次结构，采用表1中互反性1～9标度对层次结构中逐层指标进行区间标量化判断，形成图1中目标层与准则层、准则层与子准则层之间的区间判断矩阵。

(2)矩阵一致性检验。在专家经验判断时, 可能会有自相矛盾的现象，因此需对区间判断矩阵进行一致性检验；若不满足一致性要求，运用一致性修正算法进行校正或让专家重新判断，直至判断结果一致[8]。

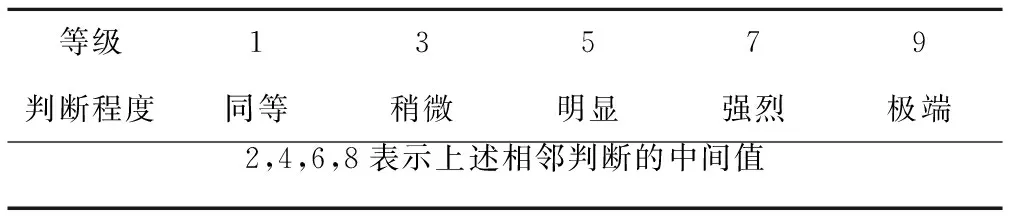
表1 互反性1～9标度Tab.1 Reciprocal 1～9 scalar system

(3)确定指标权重。判断矩阵元素均为区间数，采用区间特征根法进行权重求解。以区间数为元素的向量或矩阵称为区间数向量或区间数矩阵，它们的运算通常按照向量或数字矩阵的运算定义。设B=(bth)l×l(t=1,2,…,l;h=1,2,…,l)为区间判断矩阵，记B=[B-,B+]，有B-=(b-th)l×l，B+=(b+th)l×l，bth=[b-th,b+th]；同样，对区间向量v=(v1,v2,…,vl)，记vt=[v-t,v+t]，有v-=(v-1,v-2,…,v-l)T，v+=(v+1,v+2,…,v+l)T。按照以上定义，先计算B-和B+的最大特征值所对应的具有正分量的归一化特征向量v-、v+，之后根据式(5)、(6)计算各层次指标权重向量，确定指标权重。

(6)

2.3 应急能力度量模型构建

根据图1记水电厂突发事件应急能力度量的评价指标集为A={aj|j=1,2,…,n;n=17}，则与之对应的指标权重集为WA={wj|j=1,2,…,n;n=17}；假设有m位专家对各评价指标进行语言评价，记专家集为E={ei|i=1,2,…,m}，专家权重集为WE={wi|i=1,2,…,m}；记语言评价集S={sk|k=0,1,…,6}={极差，很差，差，一般，好，很好，极好}，且rij∈S表示专家ei对指标Aj的评价结果，并将其转化为二元语义形式(rij,0)，则可以得到专家关于评价指标的二元语义评价矩阵：

(7)

根据式(8)对专家给出的评价值进行集结，得到指标Aj的加权平均评价值：

(8)

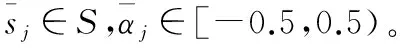
集结指标Aj的加权平均评价值和指标权重wj，按照式(9)计算层次结构各层综合评价值：

(9)

最后将目标层即应急能力度量综合评价值与最近评价语言等级相比，得出应急能力度量最终结果。

3 算 例

3.1 工程资料

某水电厂是一座以发电为主，兼顾航运、灌溉、供水等综合利用的大型水利工程，总装机容量104万kW，年均发电量27.54 亿kWh，在电力系统中主要承担调峰、调频、事故和负荷备用，同时可以提高流域干流的水能调节能力，增加下游梯级电站的发电效益。该水电厂位于深山峡谷，远离城市，交通不便，受人、机、环、管等诸多因素的影响，厂区安全隐患多、涉及面广而复杂，突发事件发生后往往危害严重，其中任何一个环节发生故障，都会带来一系列突发事件连锁反应。为降低突发事件危害影响、保障水电厂正常安全运行，以水电厂基层、中层和高层管理者作为专家团对该水电厂突发事件应急能力进行评价。

3.2 指标权重确定

采用IAHP方法确定各评价指标权重，限于篇幅，仅以目标层与准则层为例进行权重求解。专家按照表1对准则层指标重要性进行判断，经过一致性检验后，得到目标层与准则层形成的区间判断矩阵见表2。

表2 区间判断矩阵Tab.2 Interval judgment matrix

由表2可知：

然后，运用matlab计算B-和B+的最大特征值及其所对应的具有正分量的归一化特征向量v-和v+，即v-=(0.361,0.131,0.415,0.093)，v+=(0.331,0.141,0.438,0.090)；再根据式(5)得出ε=0.859，η=1.119；最后根据式(6)，得出权重向量m(Bt)=(0.340,0.135,0.423,0.102)。同理可得其他子准则层各指标关于准则层的权重，见表3。

表3 指标权重值Tab.3 Index weight values

3.3 应急能力度量

为方便信息的统计和分析，将专家团分为基层管理专家组e1、中层管理专家组e2和高层管理专家组e3三组，即m=3，设定专家权重集为{0.4,0.3,0.3}。根据客观实际，各专家组采用语言评价集{极差，很差，差，一般，好，很好，极好}对该水电厂突发事件应急能力指标进行评价。限于篇幅，仅以准则层预防与应急准备Y1及其指标为例，专家组对其语言评价结果见表4。

表4 预防与应急准备Y1的语言评价结果Tab.4 Language evaluation results of prevention andemergency preparedness(Y1)

根据式(1)将语言评价信息转换成二元语义形式，得到各专家组的评价矩阵R36：

首先根据式(8)对专家组的评价值进行集结，得到预防与应急准备Y1各指标的加权平均评价值分别为(s5,0.3)、(s5,-0.3)、(s4,-0.3)、(s5,0)、(s4,0.3)和(s4,-0.3)；再根据式(9)，计算得出准则层预防与应急准备Y1的综合评价值为Δ(4.338)=(s4,0.338)，同理可得Y2、Y3和Y4的综合评价值分别为(s3,0.083)、(s5,-0.360)和(s5,0.223)；最后结合准则层各指标权重及其综合评价值，计算目标层即该水电厂突发事件应急能力综合评价值：

4.460+0.102×5.223)=Δ(4.387)=(s4,0.387)

从数据分析可以得出，该水电厂突发事件应急能力整体水平为好。经进一步分析，预防与应急准备能力为好、应急监测与预警能力一般、应急处置与救援和应急恢复与重建能力很好。因此，该水电厂管理人员应加大应急监测与预警方面的资源投入，提高应急监测与预警能力，同时也应持续保持预防与应急准备、应急处置与救援和应急恢复与重建等方面的资源投入，保障水电厂突发事件应急能力更上一层楼。

4 结 论

本文根据国家法律法规，结合相关资料和实践经验，建立了水电厂突发事件应急能力评价指标体系，并将区间层次分析法运用于指标赋权中，充分考虑了专家经验判断的模糊性，使指标权重确定更加科学合理。同时，为解决水电厂突发事件应急能力度量中存在的模糊性问题，本文构建了水电厂突发事件应急能力的二元语义度量模型，该模型能够系统刻画水电厂突发事件应急能力，具有很好的适用性和可操作性，为水电厂运行管理人员及时发现应急能力薄弱环节提供了一种科学有效的方法。

□

[1] 江学文.水轮发电机组振动保护工程应用研究[J]. 中国农村水利水电, 2012,(6):128-131.

[2] 张冬生,虎 勇,刘广斌,等. 探究提高水电站事故应急处置能力的方法与途径[J]. 水电能源科学, 2013,31(3):69-73.

[3] 郑霞忠,邵 波,陈 玲,等.基于Euclid理论的水电工程施工安全熵评价[J].中国安全科学学报, 2014,24(6):38-43.

[4] 何晓红. 应急体系建设在水电厂安全生产管理中的运用[J].电力安全技术, 2010,12(2):1-4.

[5] 郑 琳. 高坝大库水电站地震应急预案及亟待解决的问题[J].水力发电, 2014,40(5):73-76.

[6] 姜艳萍, 樊治平. 二元语义信息集结算子的性质分析[J]. 控制与决策, 2003,18(6):754-757.

[7] 王 振, 刘 茂. 应用区间层次分析法(IAHP)研究高层建筑火灾安全因素[J].安全与环境学报, 2006,6(1):12-15.

[8] 李继乾,苏 醒,魏翠萍.区间数判断矩阵的排序及一致性改进算法[J].数学的实践与认识, 2008,38(22):147-153.