冻融条件下土壤水分入渗参数BP预报模型研究

武雯昱，樊贵盛

(太原理工大学水利科学与工程学院，太原 030024)

0 引 言

冻融土壤的水分入渗是指具有一定温度的雨水、融雪水、灌溉水垂直向下进入冻融土壤的过程[1]。冻融过程中土壤三相比例发生变化，土壤冻结水分体积膨胀导致土壤孔隙减小，连通性降低必然影响土壤水分的入渗特性。目前，冻融土壤入渗特性研究已有一定的成就，雷志栋[2]、Kelleners和Norton[3]等人在统一分析冻结区与非冻结区时，引入了土水势的概念；Thunholm[4]等人对冻结黏土的土壤水分入渗特性进行了研究分析；Zuzel和Pikul[5]用降雨模拟装置测定了深秋冻结前，冬季冻结期，春季消融期的入渗率。然而在利用冻融期土壤水分入渗参数确定冬春灌溉技术参数等方面还没有大量的研究。针对我国54%的国土面积位于季节性冻土地区[6]，本文试图通过易获得的基本理化参数预测土壤水分入渗参数，从而获得相应的灌水技术参数，为提高季节性冻土区冬季储水灌溉的灌水质量和效果提供强有力的技术支撑。

确定土壤水分的入渗参数的模型通常有Kostiakov二参数及三参数入渗模型、philip入渗模型等，而Kostiakov三参数入渗模型相对于其他两种模型可以更好地反映冻融土壤的入渗过程[7]，且基本理化参数与入渗参数之间的关系通常是非线性的，而BP神经网络有很好的非线性映射能力，可以逼近任意非线性函数，故采用BP神经网络模型预测Kostiakov三参数入渗模型中的入渗参数。本文试图基于冬季冻土期的大量田间冻融土壤入渗试验样本，通过常规理化参数确定BP神经网络的拓扑结构，建立基于BP神经网络模型的Kostiakov三参数入渗模型参数的预测模型，实现了基于土壤基本理化参数地表土壤容重、含水率及冻结土壤特有参数冻土层厚度、灌溉水温、土壤温度等常规理化参数对入渗模型参数的预报。

1 试验条件与方法

1.1 试区土壤条件

试验场地位于山西省汾河灌区，以高粱茬地作为试验田块，土壤母质是汾河冲积物，土壤类型为草甸土。耕作层深度为0～20 cm，其下的犁底层较为明显，犁底层干密度为1.383 g/cm3,犁底层之下是黏粒含量较高的砂质壤土，之下是厚度为46 cm左右的壌质砂土。表层土(0～20 cm)有机质含量为1.15%，其物理性黏粒含量占50.98%，属于壤土质地。其样本代表性试验组土壤基本理化参数见表1。

表1 样本代表性试验组土壤理化参数

1.2 试验仪器、设备

试验的主要仪器是双套环单点入渗仪，内环直径26 cm,外环直径60 cm，该设备可以实现内环自动供水和积水入渗水头自动控制，精度高。但由于气温降低到0 ℃以下后，无法埋设入渗环，而且外环直径过大，加工成本高，因此在地表封冻前加工100余套内环入渗装置一次性预埋于试验地块，外环采用80 cm×80 cm的矩形土埂代替。其他设备包括含水率、容重、地温、冻土深度测试仪器及量水设备。

1.3 试验方法

实验方案基于非冻融土壤水分入渗特性主要影响因素及冻融土壤特有影响因素而设计，包括土壤结构、土壤含水率、地温、灌溉水温、冻土深度的影响试验等。

冻融土壤水分入渗试验采用积水入渗的方法。试验在预埋于地块的入渗仪内进行，内外环积水深度控制在2～3 cm,下环深度采用20 cm(基本接近犁底层)。入渗过程中用量筒分时段测量相应时段的内环入渗量，并记录数据，当入渗率达到相对稳定时结束试验。试验用水全部为井清水。

在进行试验时，同时测量入渗土壤剖面的含水量、容重、灌溉水温，冻土深度。土壤温度采用热敏电阻测定时，应在地表封冻前将热敏电阻按不同深度预埋于土壤中，于次年的3月测取热敏电阻数值，换算成相应的温度值。

1.4 试验样本数据的建立

根据Kostiakov土壤水分入渗累积入渗量三参数模型：

I=ktα+f0t

(1)[8]

式中:I是土壤水分入渗时相应时间的累积入渗量，cm；t是土壤水分入渗时间，min；k是入渗系数，cm/min；f0是稳定入渗率，cm/min；α是入渗指数。

根据试验所记录的累积入渗量和相对应的时间，利用matlab7.0做非线性拟合，得到相对应入渗系数k、稳定入渗率f0及入渗指数α的值，即土壤入渗参数。随机列出3组冻融土壤水分入渗Kostiakov三参数模型中的参数值，如表2所示。

表2 Kostiakov三参数模型中的参数值

建立表1和表2所示入渗模型参数和土壤理化参数的一一对应关系，建立样本数据序列，本着代表性好，非奇异样点原则，最终选取100组土壤水分入渗参数资料作为建模样本，其中随机选取10组为应用实例之用，90组作为训练样本。

2 BP神经网络模型的建立

2.1 输入、输出参数的确定

选取Kostiakov三参数入渗模型中的稳定入渗率f0、入渗系数k、入渗指数α三个入渗参数作为建立的BP神经网络预报模型的输出变量。

选择对三个输出参数影响较大的土壤常规理化参数及冻融条件下特有的影响因素作为输入变量。经过对单因素与冻融土壤入渗能力[9]分析，认为冻融条件下土壤质地、地表土壤容重、0～20 cm的土壤含水率、冻土层厚度、灌溉水温度及土层5 cm处的温度对土壤水分入渗影响较大。由于本试验在同一质地条件下进行，因此本实验中质地作为常量。输入变量选择地表土壤容重、0～20 cm的土层土壤含水率、冻土层厚度、灌溉水温度及土层5 cm处的温度5个影响因素。

2.2 BP神经网络的结构与方法

在建立模型时，选取trainlm函数作为神经网络的算法，为了加快样本的收敛性要求输入输出样本数据在0～1之间，故需要对样本进行预处理。Matlab7.0提供了归一化函数premnmx以及还原函数postmamx[10]。

BP神经网络由输入层、若干个隐含层、输出层构成。一般选取具有一个隐含层的BP神经网络就足够了。输入层有5个输入参数，即5个神经元；输出层有3个输出参数，即3个神经元；隐含层节点数采用节点渐增法，先用较少数目的隐含层节点构成神经网络训练，然后根据训练精度适当增加隐含层节点，直到达到训练精度为止[11],经多次运算，隐含层节点数为35时，达到训练精度。即网络的拓扑结构为5∶35∶3。

通过分析归一化后的数据，选择S型正切函数tansig函数与线性函数purelin函数分别作为隐含层和输出层的激活函数。采用学习率为0.01，最大学习迭代次数为1 500，训练精度为0.000 1进行训练。BP模型采用误差反向传播的迭代方法，经过循环训练达到要求精度后停止。

2.3 入渗参数的预报模型

2.3.1模型结构

根据样本数据采用Matlab7.0建立的BP模型结构如式(2)所示：

net=newff(min max (traininput), [35,3],

{'tansig', 'purelin'}, 'trainlm')

(2)

式中：newff是Matlab中建立前馈神经网络的函数；traininput是指模型的输入样本；min max(traininput)指样本的范围；[35,3]中35指隐含层的神经元节点个数，3指输出层的神经元节点个数；tansig、purelin分别是隐含层和输出层的激活函数；trainlm是BP模型中的一种算法，即神经网络的反向传播训练函数。

BP神经网络的训练结果如(3)式所示：

[α,k,f0]=purelin{lw2×[tansig(iw1×p+b1)]+b2}

(3)

p=[γ,θ,π,ω,ε]

式中：iw1和lw2分别是指模型输入层到隐含层的权值和隐含层到输出层的权值；b1和b2分别是指模型输入层到隐含层和隐含层到输出层的阈值；γ指地表土壤容重；θ指0～20 cm的土壤重量含水率；π指冻土层厚度；ω指灌水温度；ε指地中5 cm土壤温度。

iw1、b1的向量值如表3所示；lw2、b2的向量值如表4所示。

2.3.2训练结果

基于matlab7.0建立的BP神经网络预报模型对100组试验数据中90组进行训练后得到入渗指数α、入渗系数k、稳定入渗率f0预测值，并与实测值计算比较后得到其绝对误差和相对误差。其结果如表5-表7所示。

从表6可以看出入渗指数α训练的相对的误差平均值为2.03%，最大值为16.1%，最小值为0%；绝对误差的平均值为0.002 4，最大值为0.019 2，最小值为0。训练精度较高。

表3 BP预报模型iw1、b1的矩阵数值表

从表7可以看出入渗系数k训练的相对的误差平均值为1.34%，最大值为6.1%，最小值为0.03%；绝对误差的平均值为0.016 8 cm/min，最大值为0.091 8 cm/min，最小值为0.000 5 cm/min。训练精度较高。

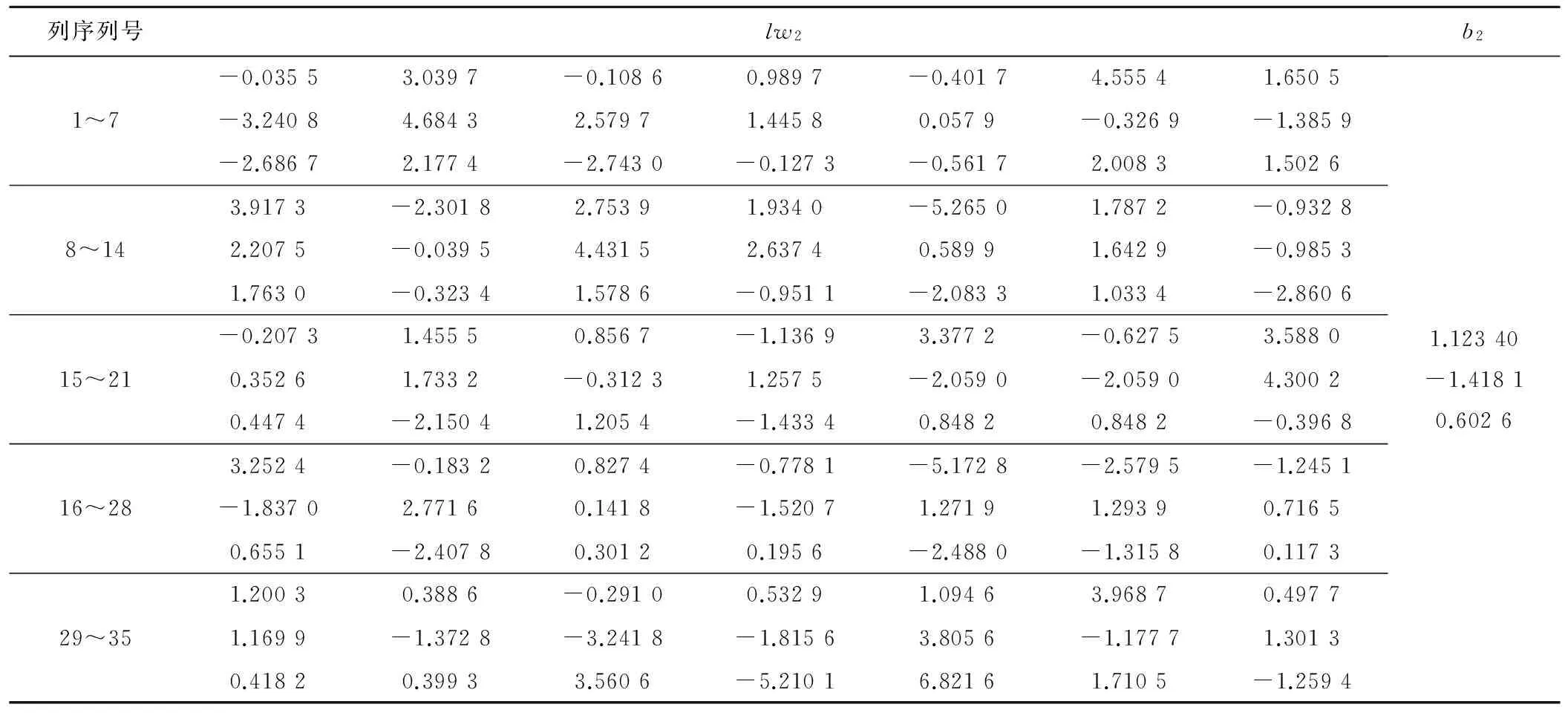
表4 BP预报模型lw2、b2矩阵数值表

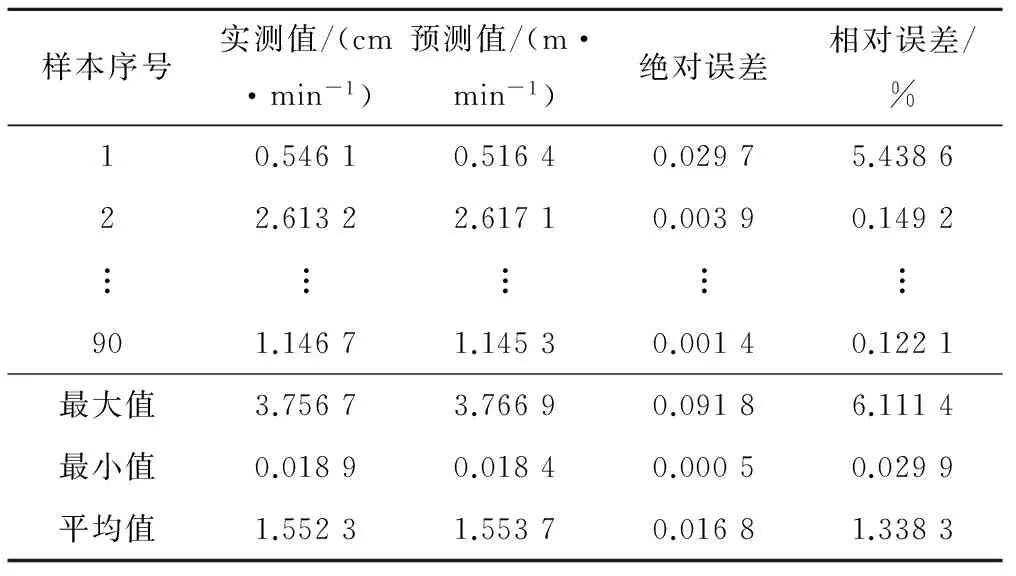
表6 入渗系数k训练结果分析表

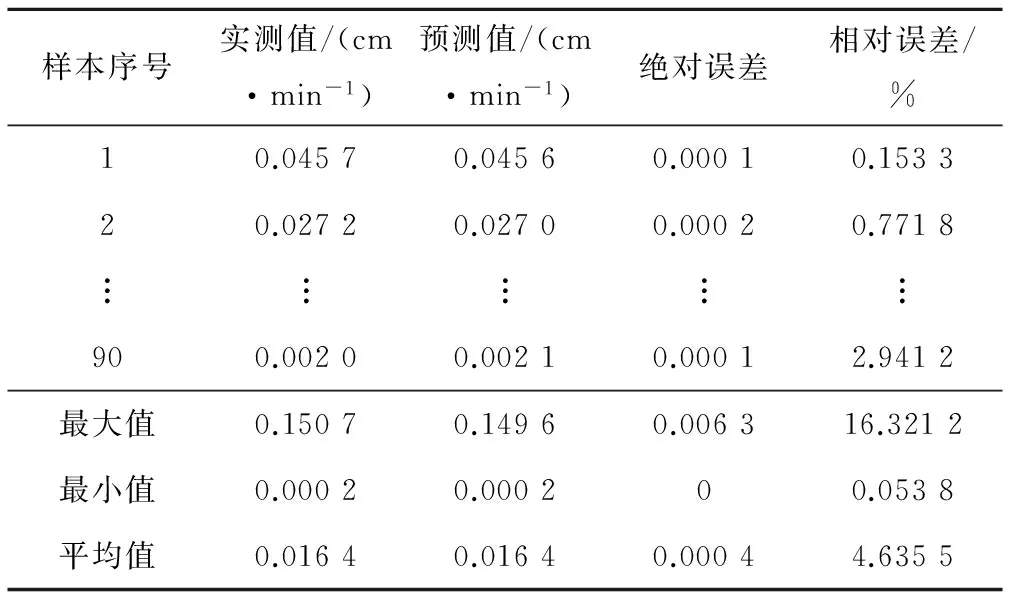
表7 稳定入渗率f0训练结果分析表

从表8可以看出稳定入渗率f0训练的相对误差平均值为4.6%，最大值为16.3%，最小值为0.05%；绝对误差的平均值为0.000 4 cm/min，最大值为0.006 3 cm/min，最小值为0。训练精度较高。

可见，基于Kostiakov三参数模型建立的BP神经网络预报模型的精度较高，有较高的可靠度。

2.3.3模型应用

用训练好的网络对校核样本的10个数据进行检验。入渗指数α、入渗系数k、稳定入渗率f0的检验结果如表8-表10所示。

表8 入渗指数α校核结果分析校核表

从表9可以看出入渗指数α校核的相对的误差平均值为1.03%，最大值为2.76%，最小值为0.19%；绝对误差的平均值为0.000 9，最大值为0.001 8，最小值为0.000 2。校核精度高于训练精度。

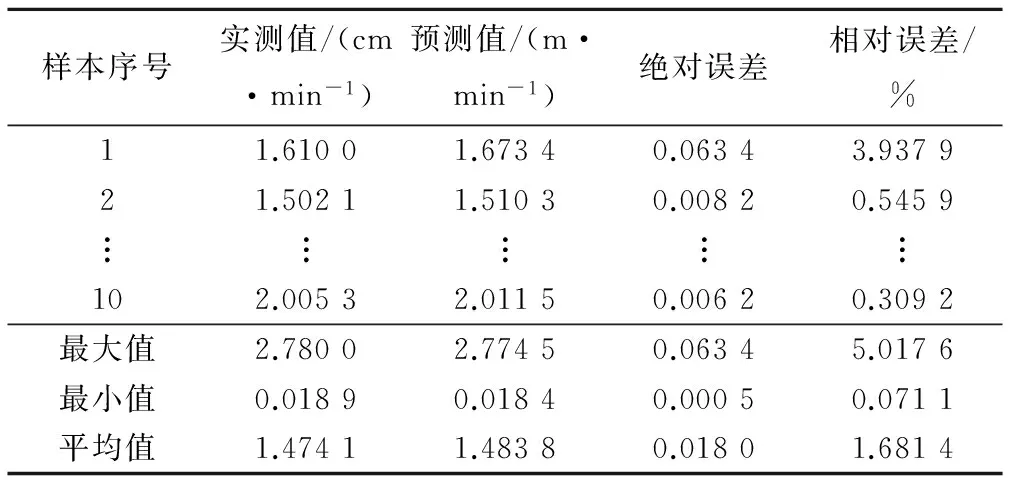
表9 入渗系数k训练结果分析表

从表10可以看出入渗系数k校核的相对的误差平均值为1.68%，最大值为5.02%，最小值为0.07%；绝对误差的平均值为0.018 cm/min，最大值为0.06 cm/min，最小值为5×10-4cm/min。校核精度与训练精度基本一致。

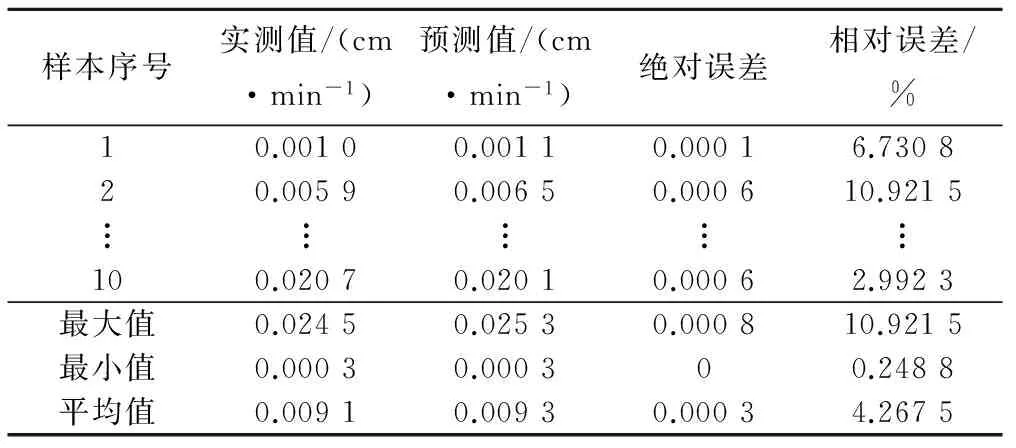
表10 稳定入渗率f0校核结果分析表

从表10可以看出稳定入渗率f0校核相对误差平均值为4.27%，最大值为10.92%，最小值为0.25%；绝对误差的平均值为3×10-4cm/min，最大值为8×10-4cm/min，最小值为0。校核精度略高于训练精度。

根据对训练结果与应用结果的分析可知，基于Kostiakov三参数模型建立的该BP神经网络可以进行冻融条件下土壤水分入渗参数的预测，且该预测结果是可靠的。

3 结 语

本文所运用BP神经网络模型预报模型可以很好地反映在冻融条件下，Kostiakov三参数模型中的土壤水分入渗参数与其基本理化参数及特有的影响因素之间的非线性关系。其训练结果及应用结果都具有高的精度。α、k及f0训练结果的相对误差平均值分别为2.03%、1.34%和4.6%；相应的应用结果误差的平均值分别为1.03%、1.68%和4.27%。这表明在冻融条件下，用基本理化参数及特有影响因素预测土壤水分入渗参数是可行的，所建模型可以为季节性冻土区冬季储水灌溉技术参数的确定提供提供有力的土壤入渗参数依据。

基于该BP预报模型，作为土壤水分入渗Kostiakov累积入渗量三参数模型中的土壤水分入渗参数α、k及f0预报输入参数的常规土壤理化参数有地表土壤容重、含水率、冻层厚度、灌溉水温及地中5 cm土壤温度。根据模型预测结果可知，所选择的输入变量能够得到较为满意的结果。

本文尝试建立基于BP神经网络的Kostiakov三参数模型参数预测模型，获得了较满意的结果，但预报模型所需要的样本数量以及训练次数都在探索中，而且BP神经网络模型主要依靠实际经验，所以还需要更加好的优化方法来设计网络模型结构，以此提高预测精度。

□

[1] 樊贵盛，郑秀清.水分在季节性非饱和冻融土壤中的运动[M].北京:地质出版社,2002.

[2] 雷志栋，尚松浩，杨诗秀，等.土壤冻结过程中潜水蒸发规律的模拟研究[J].水利学报，1999,(6):8-12.

[3] Kelleners, T J,Norton, J B.Determining water retention in seasonally frozen soils using hydra impedance sensors[J]. Soil Science Society of America Journal,2012,761.

[4] Thunholm B, L Lundin. Infiltration into frozen heavy clay soil[J]. NordicHydrology,1989:153-166.

[5] Pikul J L,Zuzel J F,Wilkins D E.water infiltration into frozen soil:field measurements and simulation[C]∥ Proceedings of the National Symposium,1991,16-17:357-366.

[6] 徐学祖,邓友生.冻土中水分迁移的实脸研究[M].北京:科学出版社,1991.

[7] 陈军锋.不同地表条件下季节性冻融土壤入渗特性的试验研究[D].太原：太原理工大学,2006.

[8] 雷志栋,杨诗秀,谢森传.土壤水动力学[M]. 北京：清华大学出版社，1988.

[9] 郑秀清,樊贵盛. 土壤含水率对季节性冻土入渗特性影响的试验研究[J]. 农业工程学报,2000,(6):52-55.

[10] 尹京川,马孝义,孙永胜,等.基于BP神经网络与GIS可视化的作物需水量预测[J].中国农村水利水电,2012,(2):13-15,18.

[11] 伍春香,刘 琳,王葆元.三层BP网隐层节点数确定方法的研究[J].武汉测绘科技大学学报,1999,(2):85-87.