Modeling of Isobutane/Butene Alkylation Using Solid Acid Catalysts in a Fixed Bed Reactor
(Research Institute of Petroleum Processing, SINOPEC, Beijing 100083)
Modeling of Isobutane/Butene Alkylation Using Solid Acid Catalysts in a Fixed Bed Reactor
Liu Zheng; Tang Xiaojin; Hu Lifeng; Hou Shuandi
(Research Institute of Petroleum Processing, SINOPEC, Beijing 100083)
A dynamic mass transfer model of isobutane/butene alkylation over solid acid catalysts in a fi xed bed reactor was established. In the model, a modi fi ed equation for the relationship between point activity and effective diffusion coef fi cient was proposed. It is found that the simulation results fi t the experimental data well and the breakthrough time of the bed layer is predicted accurately. By modeling the alkylation process, the time-space distribution of butene and point activity pro fi les of catalysts can be obtained. Furthermore, the reasons for the deactivation of solid acid catalysts were investigated. It indicates that the main reason for the deactivation of catalysts is the site coverage near the inlet of the reactor, while it is ascribed to the steric effect in the region far away from the inlet.
mass transfer model; isobutane/butene alkylation; fi xed bed reactor; deactivation; internal diffusion
1 Introduction
As a refining process, alkylation of isobutane andn-butene can provide an ideal blendstock for production of high octane fuel. The existing processes are mostly catalyzed using liquid-phase catalysts, such as sulfuric acid and hydro fl uoric acid. However, due to the inherent characteristic of liquid-phase catalysts, there are some disadvantages and shortcomings involved[1]. Thus, plenty of research efforts have been made in searching for different heterogeneous catalysts as the alternative to liquid-phase catalysts[2-3]. In particular, solid acid catalysts which show high product selectivity have been studied as potential industrial catalysts[4-6]. The major problem for the large-scale application of solid acid catalysts is the rapid catalyst deactivation[7]. Consequently, it is a matter of great urgency to investigate the alkylation process and the deactivation behavior of solid acid catalysts.
In literature, the format of the governing equations for the alkylation process and the deactivation behavior in different reactor systems have been attracting a lot of attention[8-11]. The model developed by Simpson shows that many factors, such as the isobutane ton-butene feed ratio, the olefin space velocity (OSV) and the operating temperature, could affect the alkylation process. Sahebdelfar found out that the internal diffusion limitation would promote the deactivation rate. In the research made by Hamzehlouyan, a CSTR model has been developed by implementing more appropriate assumptions and pore mouth plugging is considered as a major factor leading to the deactivation of solid acid catalysts. However, the alkylation process and the deactivation behavior of solid acid catalysts in a fi xed bed reactor have not been adequately explored. The fixed bed reactor is preferred in the practical application of alkylation process, as it could fulfill the industrial requirements, such as highly competitive economics, simple operation and the ability to retro fi t existing units[12].
In view of the above background, the present work mainly developed a dynamic mass transfer model to simulate the alkylation process and the deactivation behavior of solid acid catalysts in a fi xed bed reactor. By virtue of the model, the time-space distribution of butene and point activity pro fi les of catalysts are obtained. Upon analyzing the information gained from the modeling work, a further understanding of the reason for the deactivation of solid acid catalysts is obtained.
2 Modeling
Isobutane/butene alkylation reaction is currentlyconsidered as the mechanism of carbenium ion reaction[2]. While alkylation reaction (Eqs. 1-2) is not always the preferred reaction pathway during alkylation process, there are many side reactions which can reduce the quality of alkylates and lead to deactivation of catalysts. Side reactions will result in the accumulation of heavier carbocations which could inhibit the diffusion of species in the catalyst pellets. For making a mathematical model closer to the real application, the site coverage and steric effect which can influence the activity of solid acid catalysts should be considered.
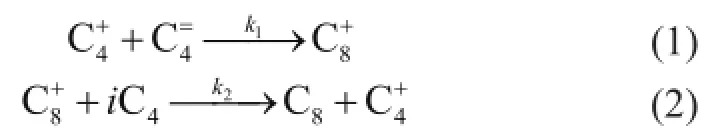
For simpli fi ed computing, Simpson established equations suitable for the butene consumption rate (Eq. (3)) and the deactivation rate of active sites (Eq. (4))[9].

By utilizing the above kinetic formulations, a mathematical model of the alkylation reaction and the deactivation process can be constructed. The schematic diagrams of the fi xed bed reactor and species diffusion in a catalyst pellet are shown as Figures 1 and 2.
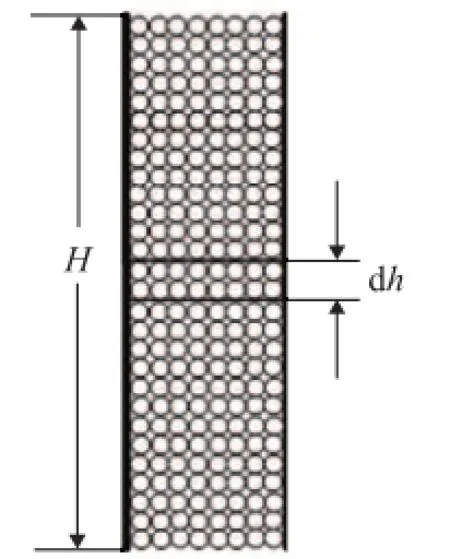
Figure 1 The schematic diagram of the fi xed bed reactor
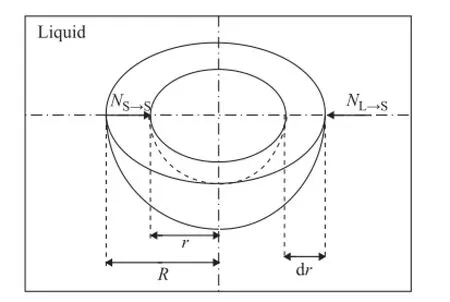
Figure 2 The schematic diagram of species diffusion in a catalyst pellet
For modeling isobutane/butene alkylation in a fixed bed reactor, four assumptions should be identified: (1) The bulk fl ow in the bed is a plug fl ow; (2) The catalyst pellets in the bed are distributed uniformly; (3) The external diffusion is ignored; and (4) The alkylation reactions occur in catalysts. According to the assumptions mentioned above, the reactor bed is divided intoNcells of equal volume for the purpose of numerical computing and each cell is well mixed. The material balance equation of the bulk fl ow in the fi xed-bed reactor can be written as:

whereCB,CA,iare the intra-pellet and bulk butene concentration, respectively. Moreover,Uis the velocity of the bulk flow,εlandεsrespectively represent the void fraction of bed and pellets in the reactor,Deffis the effective intra-pellet diffusion coef fi cient of butene.
The radius of the catalyst pellet is divided intoMequal intervals, and the mass balance of butane in a spherical catalyst pellet in each cell of the reactor can be written as follows:

whereεpis the pellet porosity, andCB,mrepresents butene concentration in themth shell of the pellet.
The local effective diffusion coef fi cient is assumed as a function of local activity of the catalyst pellet and can be written as[10]:
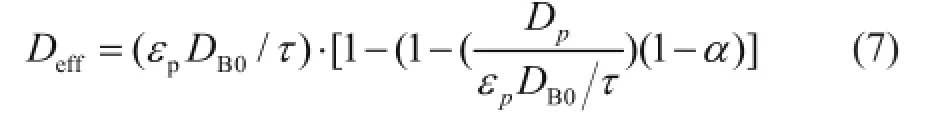
whereτis the tortuosity of the pellet,αis the point activity,DB0is the effective diffusion coef fi cient of butene in clean pores andDpis the effective diffusion coef fi cient in the completely poisoned area.
Eq. (7) can be modi fi ed to Eq. (8):
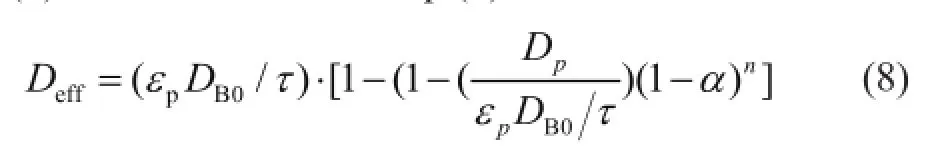
wherenis an index representing the effect of the point activity on the effective diffusion coefficient. Eq. (8) reveals the steric effect, while Eq. (4) describes the site coverage.
In order to simulate the process of mass transfer in the reactor, the boundary and initial conditions are expressed as follows:
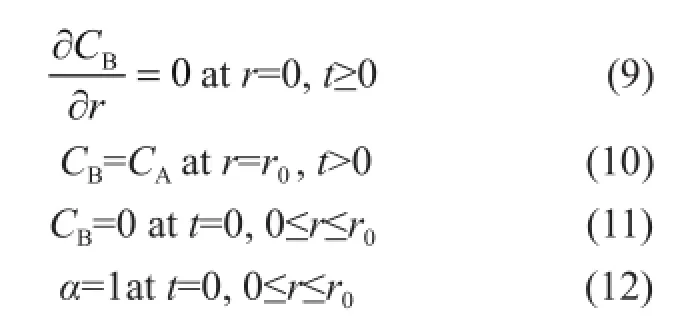
For solving the olefin material balance model,k1,K,k3,nandDpare set as adjustable parameters. The values of the above parameters can be computed by fitting the calculated results of the model to experimental values using the least square function (Eq. (13))
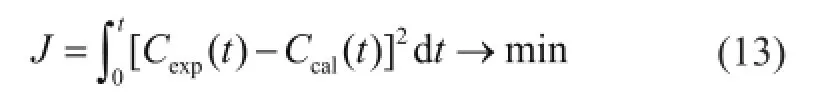
whereCexpandCcalare the experimental and the calculated concentration values, respectively.
3 Results and Discussion
Zuazo[13]researched the alkylation process of isobutane and butene on the FAU zeolite in a fi xed-bed reactor at a pressure of 20 bar and a temperature of 75 ℃, with OSV equating to 0.2 h-1. The other operating parameters in his work are depicted in Table 1.

Table 1 Values of parameters for modeling[13]
In literature, the value ofnin Eq. (8) was considered as a fi xed value of 1 and the form of the equation is expressed as Eq. (7)[10-11]. Becausenrepresents the influence of point activity on the effective diffusion coefficient, different values ofncould lead to different calculated results as shown in Figure 3. In case of a lower value ofn(n=0.25), butene would penetrate the catalyst bed layer in a shorter time, while it would penetrate the bed layer in a longer time when the value is higher. In other words, in the former case, the point activity has greater influence on the effective diffusion coefficient than that of the latter case. In real application, the operating period of a fi xed bed reactor is determined by the breakthrough time and then catalysts are necessary to be regenerated. Taking unsuitable values ofnwould underestimate or overestimate the effect of point activity on the effective diffusion coef fi cient, which would lead to miscalculation of breakthrough time. Therefore, an accurate evaluation ofnis essential to predict the breakthrough time.

Figure 3 Experimental[13]and calculated buteneconversion for different values ofn
Figure 4 shows the experimental data of Zuazo and the predicted data obtained from the present model and Hamzehoulouyan’s model[11]. When the conversion of butene is 100%, the present model is accurate enough, while there is a slight error in the region when the bed layer is penetrated. It indicates that the present model could simulate the alkylation process in a fixed-bed reactor quite well and predict the breakthrough time of the bed layer accurately. As the operating period of the reactor is determined by the breakthrough time in industrial application, the present model is more practical.
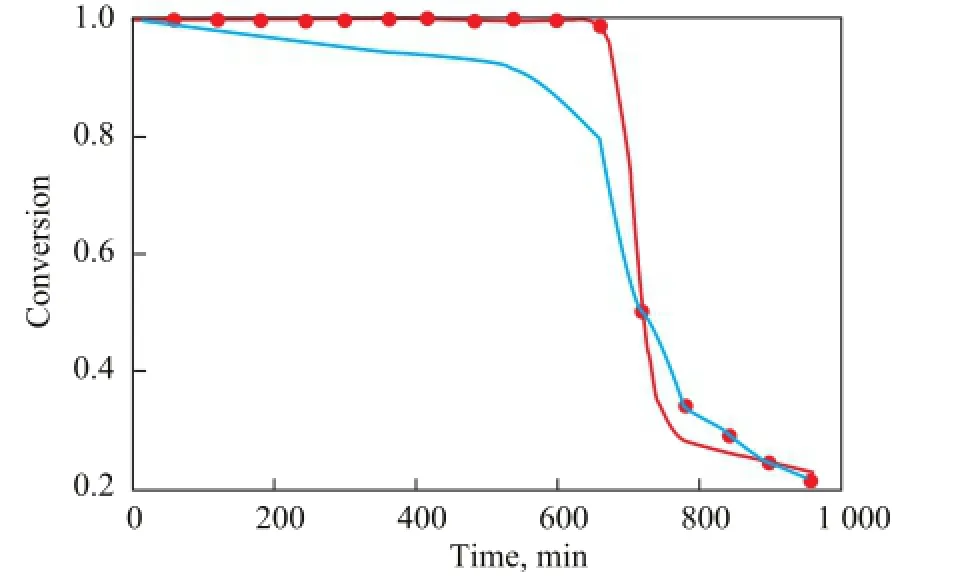
Figure 4 Experimental[13]and calculated butene conversion rates of different models
Figure 5 shows the point activity pro fi les of catalysts inthe reactor. Intra-pellet point activity values dropped fast to zero at the place near the inlet of the reactor, while the point activity values in the inner layer of catalysts would remain at a certain value in the upper place of the reactor. It can be found that the farther the catalysts from the inlet of the reactor are, the more obvious the effect of steric hindrance on diffusion of butene is.

Figure 5 Point activity versus time at various heights away from the inlet of the reactor.
Three formats to describe the mean activity of the catalyst pellets are applied: the fi rst is the resting activity of a single catalyst, the second is the resting activity of the whole catalysts, and the last is the effective resting activity of the whole catalysts which can take part in the reaction. The three activity values can be calculated respectively as follows:
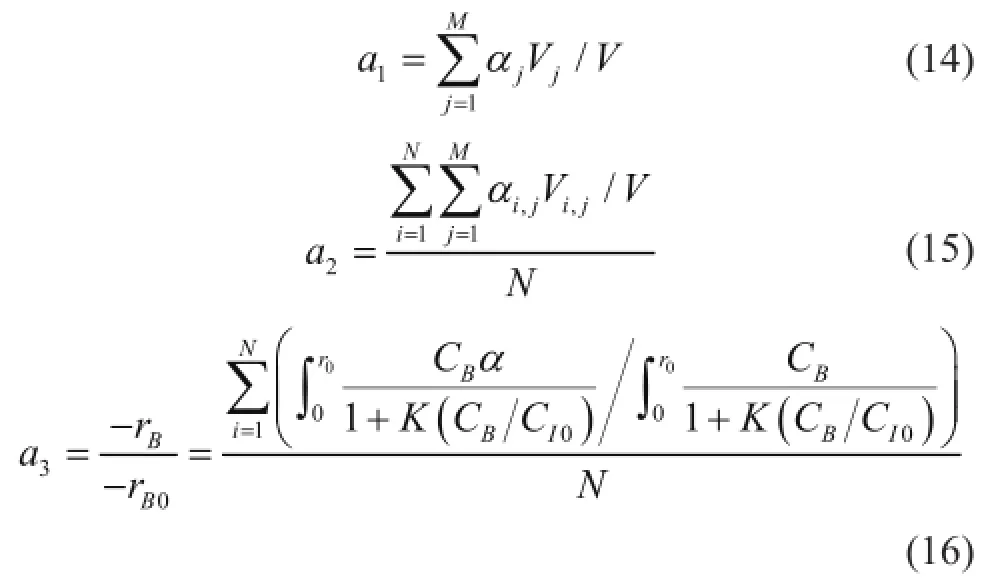
whereNandMrepresent theNth andMth cell of the reactor and the catalyst pellet, respectively. Furthermore,Vjis thejth volume of single pellet,Vis the volume of a single catalyst, and (-rB0) is the rate of the alkylation reaction in the fresh catalyst.
Figure 6 shows the time-space distribution ofa1. Upon combining with Figure 5, it was found that the alkylation reaction occurred at a certain height. When butene reaches a certain height of the reactor, butene would rather diffuse into the pellets than flowing to the higher place of the reactor due to the effect of diffusion. Furthermore, catalysts in the upper part of the reactor still have good activity until the experiment fi nishes.
Figure 6 The time-space distribution ofa1
Comparison on the variation ofa2with that ofa3is shown in Figure 7. As illustrated in the Figure 7, the former was higher than the latter after 400 minutes. This indicates that steric effect plays an important role in deactivation of catalysts.

Figure 7 Different kinds of pellet activity versus time
Near the inlet of the reactor (see Figure 8), trends of local point activity and butene concentration in a catalyst pellet tend to be similar, while there is an apparent difference at the higher place of the reactor (see Figures 9, 10, and 11). Butene concentration gradient between in and out of catalyst pellets is large near the inlet because of step change of butene concentration leading to a great diffusion driving force. In this way, local concentrationof intra-pellet butene would quickly become the same as that of bulk butene (see Figure 8(b)). Therefore the steric hindrance could be neglected and the site coverage becomes the main reason for the deactivation of catalysts near the inlet. Catalysts are poisoned completely (see Figure 8(a)).
At the higher place of the reactor (see Figures 9(b), 10(b), 11(b)), the bulk butene concentration increases from zero gradually instead of a step change. When butene reaches a certain height of the reactor, it would diffuse into the pellets and the alkylation reactions start. In the beginning, the alkylation process depends on the diffusion of butene the rate of which is much larger than the rate of the reaction. At this stage, the intra-pellet butene concentration increases quickly. As the reactions proceed, the solid acid catalysts lose activity and the heavier carbocations would block the pores of pellets gradually. With the resultant steric hindrance, the diffusion driving force decreases and it is difficult for species to diffuse into the inner layers of catalysts. During this period, the reaction rate is much larger than the diffusion rate causing rapid consumption of intra-pellet butene in inner layers of catalysts. With the deactivation of point activity in outer layers of catalysts, the reaction rate decreases gradually and the species restart to diffuse into inner layers which would induce the accumulation of intra-pellet butene. At the end of the alkylation process, the local concentration of intra-pellet butene tends to be stable at different values being lower than the bulk butene concentration, and the inner layers of catalysts located at the higher place of the reactor still have good activity (see Figures 9(a), 10(a), and 11(a)). Therefore the steric effect is the main reason for deactivation of catalysts in the region that is far away from the inlet. Furthermore, the farther the catalysts from the inlet of the reactor are, the more obvious the steric effect is.
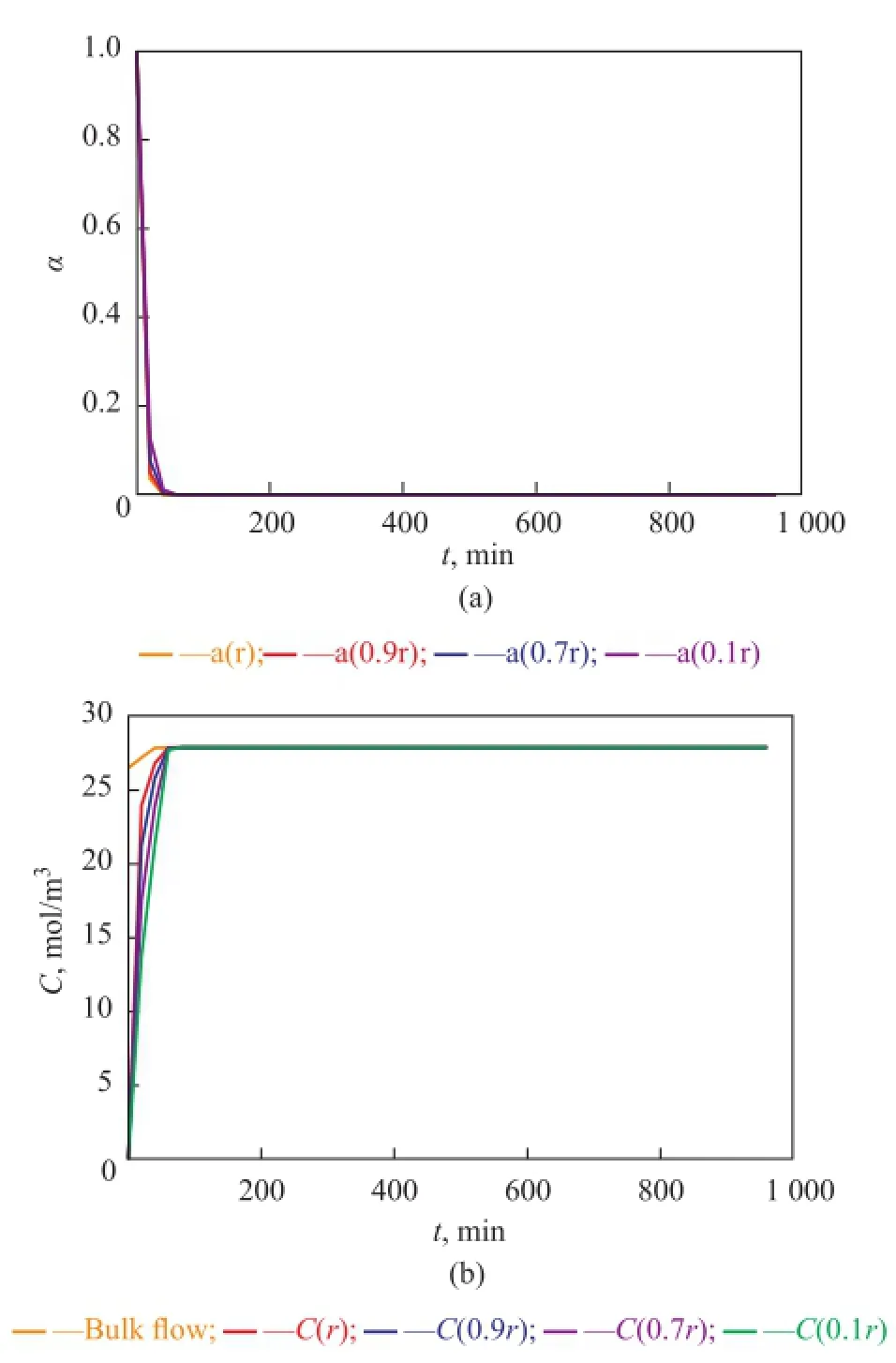
Figure 8 Point activity and concentrations of bulk and intra-pellet butene versus time at a height of 0.1 cm away from the inlet of the reactor

Figure 9 Point activity and concentrations of bulk and intra-pellet butene versus time at a height of 3 cm away from the inlet of the reactor
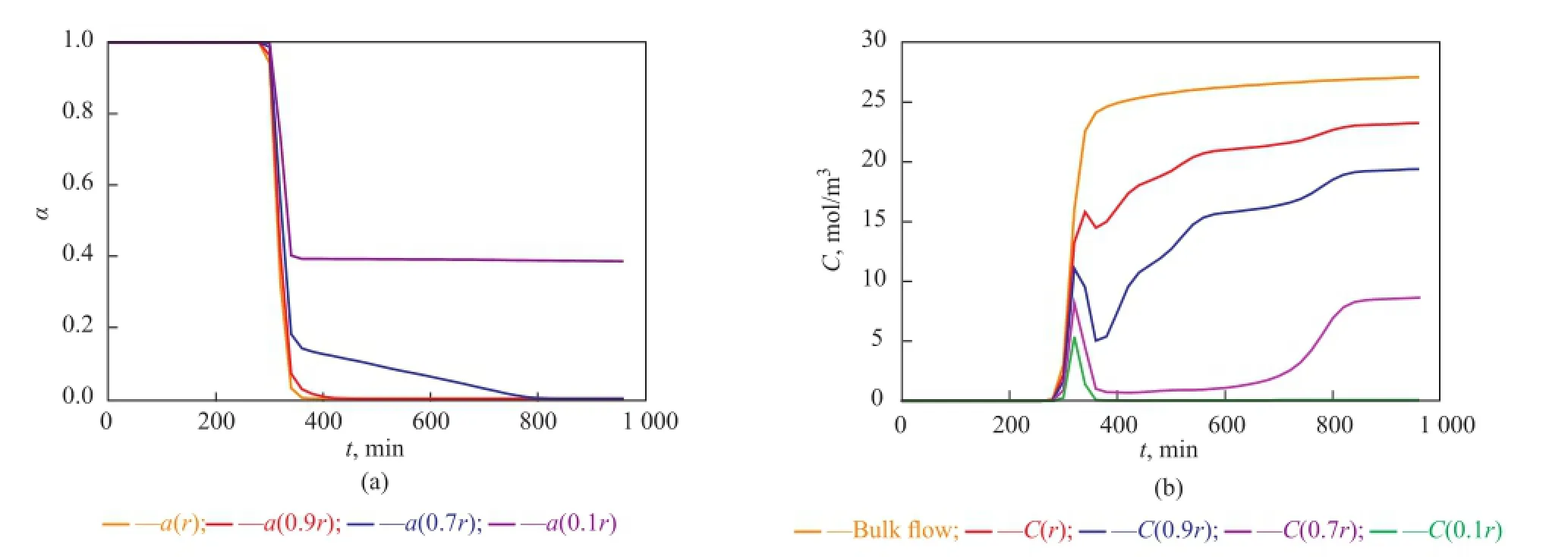
Figure 10 Point activity and concentrations of bulk and intra-pellet butene versus time at a height of 4 cm away from the inlet of the reactor
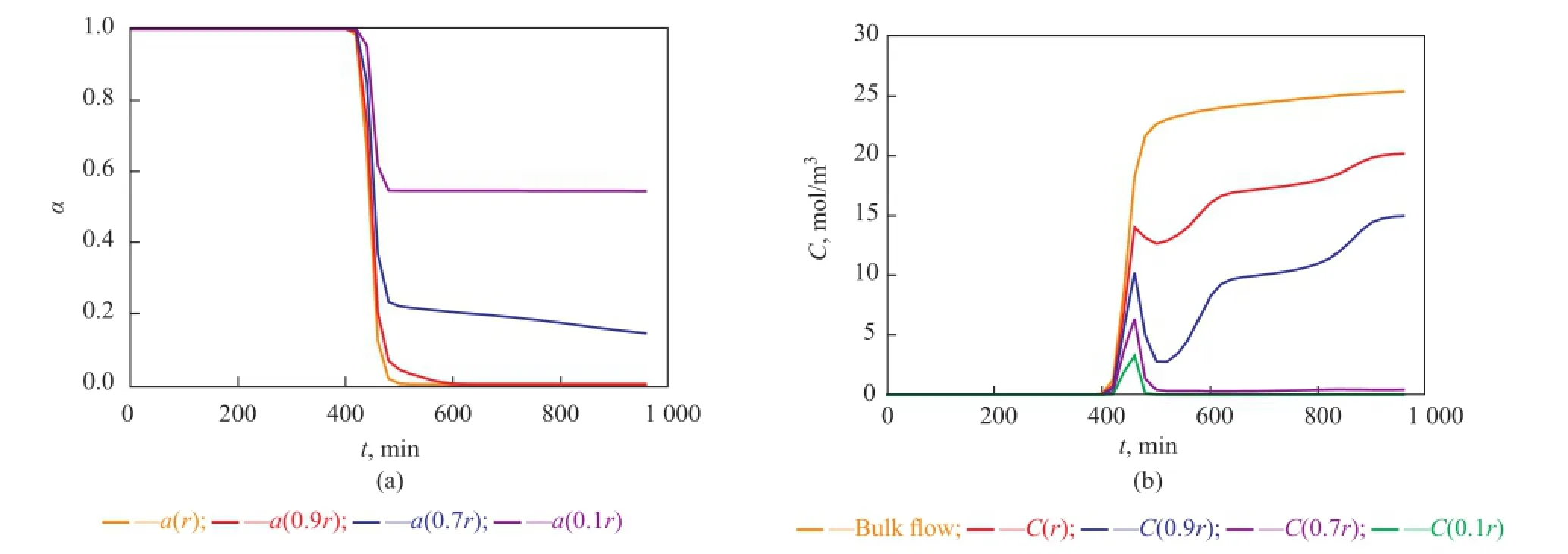
Figure 11 Point activity and concentrations of bulk and intra-pellet butene versus time at a height of 5 cm away from the inlet of the reactor
4 Conclusions
A dynamic mass transfer model was developed for the isobutane/butene solid acid alkylation process in a fi xed bed reactor. A modified equation for the relationship between effective diffusion coef fi cient and point activity was proposed. Upon utilizing the modi fi ed equation, the simulation results could fit experimental values better and the breakthrough time could be predicted accurately. Also, the model could provide the time-space distribution of butene concentration and point activity pro fi les.
The alkylation reaction occurred at a certain height in a fixed-bed reactor. Catalysts in the upper place of the reactor still had good activity after the breakthrough time of the fi xed bed.
Based on the trends of local point activity and butene concentrations, reasons for the deactivation of solid acid catalysts were well understood. It indicates that the main reason for the deactivation of catalysts is the site coverage near the inlet of the reactor, while it is caused by the steric effect in the region that is far away from the inlet.
[1] Rao P, Vatcha S R. Solid-acid alkylation process development is at crucial stage[J]. Oil and Gas Journal, 1996, 94(37): 56-61
[2] Corma A, Martinez A. Chemistry, catalysts, and processes for isoparaf fi n–ole fi n alkylation: Actual situation and future trends[J]. Catalysis Reviews—Science and Engineering, 1993, 35(4): 483-570
[3] Sarsani V R, Wang Y, Subramaniam B. Toward stable solid acid catalysts for 1-butene+isobutane alkylation: Investigations of heteropolyacids in dense CO2media[J].Industrial & Engineering Chemistry Research, 2005, 44(16): 6491-6495
[4] Clark M C, Subramaniam B. Extended alkylate production activity during fixed-bed supercritical 1-butene/isobutane alkylation on solid acid catalysts using carbon dioxide as a diluent[J]. Industrial & Engineering Chemistry Research, 1998, 37(4): 1243-1250
[5] Feller A, Lercher J A. Chemistry and technology of isobutane/alkene alkylation catalyzed by liquid and solid acids[J]. Advances in Catalysis, 2004, 48: 229-295
[6] Taylor R J, Sherwood D E. Effects of process parameters on isobutane/2-butene alkylation using a solid acid catalyst[J]. Applied Catalysis A: General, 1997, 155(2): 195-215
[7] Weitkamp J, Traa Y. Isobutane/butene alkylation on solid catalysts. Where do we stand?[J]. Catalysis Today, 1999, 49(1): 193-199
[8] De Jong K P, Mesters C, Peferoen D G R, Van Brugge P T M. Paraf fi n alkylation using zeolite catalysts in a slurry reactor: Chemical engineering principles to extend catalyst lifetime[J]. Chemical Engineering Science, 1996, 51(10): 2053-2060
[9] Simpson M, Wei J, Sundaresan S. Kinetic analysis of isobutane/butene alkylation over ultrastable HY zeolite[J]. Industrial & Engineering Chemistry Research, 1996, 35(11): 3861-3873
[10] Sahebdelfar S, Kazemeini M, Khorasheh F, Badakhshan A. Deactivation behavior of the catalyst in solid acid catalyzed alkylation: effect of pore mouth plugging[J]. Chemical Engineering Science, 2002, 57(17): 3611-3620
[11] Hamzehlouyan T, Kazemeini M, Khorasheh F. Modeling of catalyst deactivation in zeolite-catalyzed alkylation of isobutane with 2-butene[J]. Chemical Engineering Science, 2010, 65(2): 645-650
[12] Jensen A B, Hommeltoft S I. Recent developments in fixed-bed alkylation FBATM[C]//NPRA Annual Meeting, AM-03-24, San Antonio, TX, 2003
[13] Zuazo I. Deactivation routes in zeolite catalyzed isobutane/2-butene alkylation and regeneration procedures[D]. Universität München, 2004
Received date: 2016-03-11; Accepted date: 2016-05-20.
Dr. Tang Xiaojin, Telephone: +86-10-82369270; E-mail: tangxj.ripp@sinopec.com.
- 中国炼油与石油化工的其它文章
- Synthesis and Evaluation of Environmentally Friendly Calcium Isostearate Detergent with Excellent Oil Solubility
- Electrospinning Preparation and Mechanical Properties of Polymethyl Methacrylate (PMMA)/Halloysite Nanotubes (HNTs) Composite Nano fi bers
- Study on the Adaptability of Etheri fi cation Feedstock to Reactor Type
- Analysis and Modeling of Wangqing Oil Shale Drying Characteristics in a Novel Fluidized Bed Dryer with Asynchronous Rotating Air Distributor
- Experimental and Molecular Simulations for Evaluating the Effect of Lubricity Improvers on the Property of Jet Fuel
- Preparation and Tribological Properties of Lanthanumdoped Muscovite Composite Particles as Lubricant Additives in Lithium Grease

