“画”里有“话”

夏光杰

苏教版教材修订后首次出现的“用画线段图整理条件和问题，分析数量关系的策略”这一教学内容，为准确了解学情，笔者编写了一道类似例题的和差问题，在任教的两个班分别做了课前调查，统计结果如下：

两个班级均为笔者任教班级，班级整体水平相当。通过调查、对比表（一）和表（二）中的统计数据，四（2）班学生解答正确率明显高于四（1）班，仅题目呈现方式的不同，正确率相差就如此之大，不难看出图示直观对厘清数量关系及支撑数学思考的有效性。

表（一）和表（二）反映出学生除了使用教材呈现的解题方法外，也出现了教材中没有提及的方法，如20÷2=10（元），4÷2=2（元），10-2=8（元），10+2=12（元）。如果学生出现了这样的解法，课堂教学中就有必要让学生进行对比，思考解法上的异同点。

表（一）中的统计数据表明，在没有学习和差问题的情况下，四（1）班有33.3%的学生能够正确解答。课堂教学既要面向全体学生，也要关注个体差异，那么在课堂教学中，如何能让这部分学生也能体验到画图策略解决问题的价值？同时从表（一）中也能发现当学生遇到陌生问题情境，或者自己难以清晰理解题意的情况下，少部分学生有自主尝试画图分析问题的需求和已有经验，但仅占全班人数的15.2%，这种能力需要教师的精心呵护和用心培养。

针对课前调查和统计分析，教师确定了本节课的教学目标：初步学会用画线段图的方法整理条件和问题，能读懂线段图，能借助线段图帮助分析数量关系，确定解题思路，并能正确解答相关的实际问题；在解决问题的过程中，发展几何直观，感受画图描述和分析对解决稍复杂问题的价值，进一步积累解决问题的经验。为更好地还原教学实践过程，现撷取部分教学片段以便分析总结。

【片段1】导入环节，激发需求

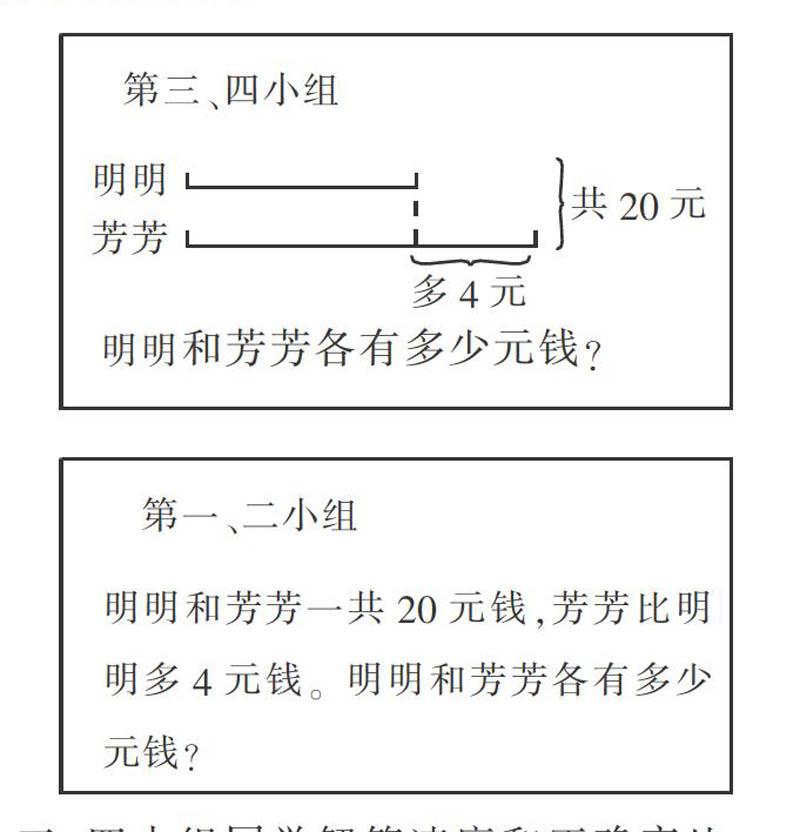
课前小组PK赛：

[明明][芳芳] [共20元][多4元][明明和芳芳各有多少元钱？][第三、四小组] [明明和芳芳一共20元钱，芳芳比明明多4元钱。明明和芳芳各有多少元钱？][第一、二小组]

师：三、四小组同学解答速度和正确率比一、二小组好，三、四小组获胜！

（第一、二组学生）众：不公平，他们组有图。

师：有图怎么啦？

生：图更简单，更直观，能搞清楚数量关系……

师：今天这节课要解决的实际问题，同学们希望老师用什么方式呈现？

生（众）：线段图。

多媒体出示，文字描述的方式呈现例题：小宁和小春一共有72枚邮票，小春比小宁多12枚，两人各有多少枚邮票？

师：很遗憾，老师没有给你们准备，该怎么办？

生：自己画。

师：自己动手，好想法。如果有困难可以同桌交流，相互帮助。

【片段2】对比方法，交流体会

观察画好的线段图，交流可以先算什么。如课前调查情况一样，几乎都想到将多的12枚邮票减掉，用剩下的60枚除以2得到小宁30枚，再求出小春有42枚。此时，教师引导学生再次观察线段图并启发。

师：为什么先减掉12枚？

生1：这样就好平均分了。

生2：这样两人就同样多了，除以2就能算出小宁的邮票枚数。

师：同学们想得很棒，想到使他们变得同样多后再平均分。除了可以用减掉12枚的方法能使两人同样多以外，还有其他能使两人同样多的办法吗？

生3：我觉得还可以将小宁增加12枚，他们也能变得一样多。（生点头赞同）

生4：如果小春将多出来的12枚，平均分成两份，给一份给小宁，他们也同样多。（生鼓掌赞同）

接着，学生选择自己喜欢的方法解答。师选择三种有代表性的解法让学生板书到黑板上。

[多12张] [共有72张] [60张][72-12=60（张）

60÷2=30（张）

30+12=42（张）

答：小宁30张，小春42张。] [小宁][小春][小宁][小春] [多12张] [共有72张] [60张][72+12=84（张）

84÷2=42（张）

42-12=30（张）

答：小宁30张，小春42张。]

对比交流：方法一和方法二，想法上有什么相同？做法上有什么不同？

生5：方法一是减掉12张，方法二是加上12张。

生6：都是要变成同样多后再平均分。

生7：方法一先算出小宁的，方法二先算出小春的。

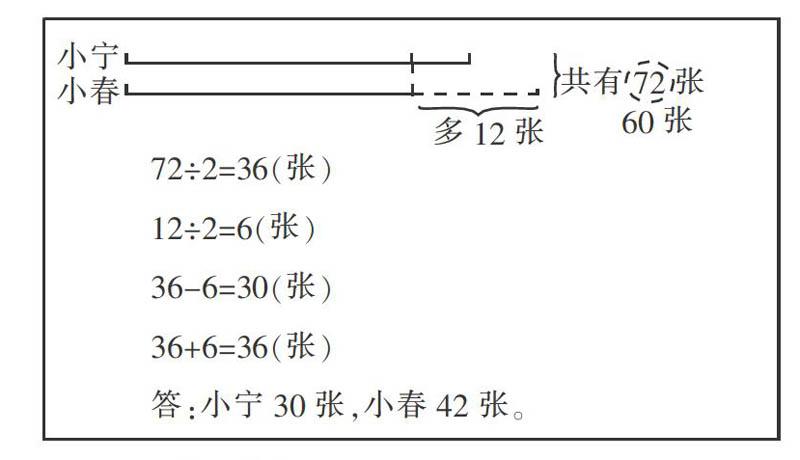
师：同学们说得真不错，抓住了问题的本质，线段图上也体现得很直观。第三种方法与前两种想法又有什么相同和不同的地方呢？

[多12张] [共有72张] [60张][72÷2=36（张）

12÷2=6（张）

36-6=30（张）

36+6=36（张）

答：小宁30张，小春42张。][小宁][小春]

……（思考片刻后）

生8：这里也是把他们变成同样多。

生9：但是这里总数72张没变，刚才两种方法中邮票总数都变了。

师：咦！这里为什么总数没变呢？

生：小春分6枚给小宁，邮票总数没变，但是刚才的假设都是拿掉12枚，或者借来12枚，所以总数变了。

师（向一、二小组同学）：课前PK题和例题类似，为什么现在都能做出来了？

生1：看图很简单。

生2：看图让我明白了为什么要减12枚……

师（向三、四小组同学）：你们还有什么体会？

生：我原来会一种方法，现在听懂了三种方法。

师：你们这些体会和感受是谁带给你的呢？

……

师：同学们以后在分析、解决问题的时候，又多了一个很好的帮手，画图策略我们以前用过，今天也在用，以后还要用下去。同学们以后会经常想起用画图的方法帮助自己解决问题吗？

教学前通过调查分析找准了学生的认知起点，用PK赛为诱导，诱发出学生图示直观的内在需求。四年级学生的抽象思维能力还在逐步形成和成长之中，在学习和思考问题时更多地借助形象思维，借助实物操作或者具体的图形、图像，他们解决问题的经历和经验还不够丰富，这给理解题中较复杂的数量关系带来很大困难。教学中先调起学生想看线段图而又没有直接呈现的悱愤状态，激发出学生想自己动手画线段图来表示题中数量关系的想法，意在调动学生积极动手操作。在动手操作的过程中，必然伴随着学生自主地动眼观察、动脑思考。借助画线段图的过程，能将抽象的语言文字化为具体、形象、直观的图形表达，从而较好地分析和解决复杂的实际问题。数学课程标准将“利用图形描述和分析问题”界定为几何直观。通过与学生交流后发现，学生能够感受到借助几何直观可以把复杂的数学问题变得简明、形象，有助于探索解决问题的思路。

直观可以付诸感官的直接感知，但直接感知到的未必就有“直观”的含义，这取决于主体的认知水平和既有的经验积累。在教学实践中，我们通过片段2的描述可以看到，都是借助线段图，不同的学生想到的方法有所不同，层次也有所不同。笔者认为，教学中渗透几何直观，能够帮助学生养成主动地想到用形象、直观的图形帮助思考、探索数学问题，从而逐渐直观地理解数学。

几何直观的教学价值还在于可以化知识为能力。线段图不但有利于学生从视觉形象的角度来表征数学问题，直观、清楚地抓住思考问题的关键，有效避免学生感知疏忽和意识模糊，更能进一步帮助学生一下子抓住问题的本质进行思考和解答，提高学生的理解能力，促进学生的思维发展，是行之有效的解决问题的策略。正如数学课程标准中所说：“几何直观可以帮助学生直观地理解数学，在整个数学学习过程中都发挥着重要作用。”这是学生第一次学习用画线段图帮助分析题意，其实在此之前的学习中已经用过画图策略认识倍数、研究周长、面积等；现在学习用画线段图分析数量关系，画图解决面积变化问题等；之后还会不断用到画线段图解决行程问题，用画图策略解决倒推问题，结合画图和替换策略解决问题，画图直观分析分数的实际问题及长方体、正方体、圆柱、圆锥等立体图形的表面积和体积问题，等等。可以说使学生养成用图形语言的直观方法来分析问题、解决问题的习惯，有助于提升学生解决问题的能力，同时还有助于培养学生的符号意识和模型思想。

作为数学教师，我们应该有这样的认识，引导并培养学生用图形来理解和阐释数学对象的含义，使几何直观贯穿整个数学学习过程。这是一个长期的、循序渐进的过程，不断使学生积累起丰富的几何直观经验，有助于提升学生的数学素养。♪