一种多系统组合导航快速选星方法

马宏阳，程鹏飞，李 冉，黄华东

（1．中国测绘科学研究院，北京100830；2．中国测绘产品质量检验测试中心，北京100830；3．山东科技大学，山东青岛266510）



一种多系统组合导航快速选星方法

马宏阳1，程鹏飞2，李 冉3，黄华东3

（1．中国测绘科学研究院，北京100830；2．中国测绘产品质量检验测试中心，北京100830；3．山东科技大学，山东青岛266510）

摘 要：采用多卫星导航系统组合导航，定位精度和系统可靠性会大幅提升，但导航定位运算量也会成倍增长。为解决多系统组合导航定位精度与实时性之间的矛盾，提出一种新的选星方法。新方法不追求最小GDOP值，而是以满足导航定位精度的GDOP值为前提，结合模糊理论中隶属函数的思想，按卫星在星座中均匀分布为原则进行选星。推导伪距测量的误差模型，分析了GDOP与测量误差之间的关系。北斗、GPS和GLONASS三系统组合导航选星实验结果表明，在不超过3次求解GDOP值的情况下，新方法能以不小于98%的概率得到GDOP≤4。

关键词：卫星导航系统；选星；隶属函数；几何精度因子

目前，美国的GPS和俄罗斯的GLONASS是公认的全球卫星导航系统［1］。中国的北斗卫星导航系统（BeiDou／Compass Navigation Satellite System）的组网卫星达到14颗，已经具备向亚太地区用户提供服务的能力［2－3］。欧盟的伽利略（GALILEO）卫星导航系统也在积极筹建。不久的将来，由这些卫星导航系统组成的全球导航卫星系统（Global Navigation Satellite System，GNSS）的卫星总数将达到100多颗，多卫星导航系统的组合导航已成为重要的发展趋势［4］。采用多星座卫星导航系统，可大幅增加可见星，定位精度和系统可用性及可靠性也会大幅提高，但导航定位的运算量也会随之成倍增长。对于高动态用户而言，为了确保数据处理的实时性，对接收机处理器的性能提出更高要求，这会使其成本上升。而实际上，不可能也不需要采用所有可见星来进行导航定位，只需选出满足定位精度要求的少数卫星进行导航定位即可。因此，在多星座卫星导航定位系统中，选星变得迫切而重要。

在卫星导航定位解算中，影响定位精度的关键因素之一是几何精度因子（Geometric Dilution of Precision，GDOP）。传统的选星方法虽然能够找出在规定卫星数目下具有最小GDOP值的卫星组合，但计算量大，对于多星座卫星导航系统而言，几乎不可能做到实时选星。针对卫星导航选星问题，文献［5］给出一种近似加权GDOP准则下的自适应阵选星方法；文献［6］给出一种利用INS辅助GPS选星算法；文献［7］将神经网络自回归模型应用到GPS选星当中。但是它们或是使用的选星规则模糊不清，导致算法的不确定性增加，或是在可见星较多时计算量仍较大，或是需要选取的卫星数较多，这使得它们在高动态多系统组合选星中存在不足。

本文利用卫星星历提供的卫星位置等信息，在站心坐标系下，以卫星高度角大小区分为前提，以卫星在星空视图中均匀分布为原则，结合模糊理论中的隶属函数，提出了一种新的选择导航卫星的方法，与其他选星方法不同的是，该方法不以追求最优GDOP值为目标，而是将GDOP值作为设计要求设定其限定值。只要选择的星座GDOP值不超出该限定值，就认为选择的星座满足要求，可以使用该星座进行导航定位。同时，为了减少过多冗余信息并在定位精度和导航计算量之间进行均衡处理，该方法还可以设定最大选星次数。

1　GDOP与导航定位的关系

1．1 GDOP与导航定位精度

伪距定位的原理为接收机不断接受卫星发射的定位信息，就可以得到其相对于卫星的测量距离（伪距）。在一个历元中伪距观测模型为［8］

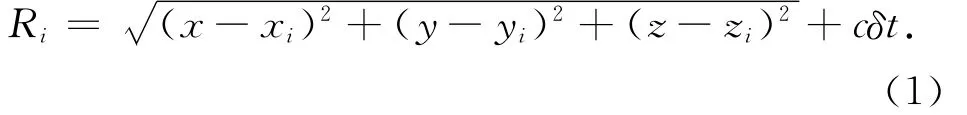
式中：Ri为接收机相对于第i颗卫星的距离量测值；（x，y，z）为接收机的三维位置；（xi，yi，zi）为第i颗卫星在该历元的三维位置；c为光速；δt为信号传播时间。值得注意的是，该观测模型是为方便进行GDOP分析而建立的，其中并没有考虑卫星钟差、接收机钟差、对流层和电离层延迟、多路径等误差。对式（1）进行Taylor展开并忽略高阶项，得到该模型的伪距观测误差可近似表示为

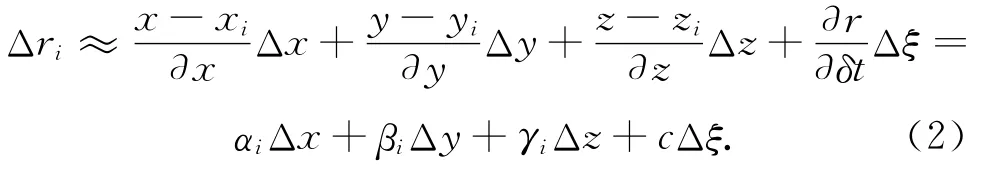
式中：（Δx，Δy，Δz）为接收机三维位置估计值；Δξ为测量噪声；r＝，为该历元接收机与卫星间的真实距离。式（2）用矩阵表示为

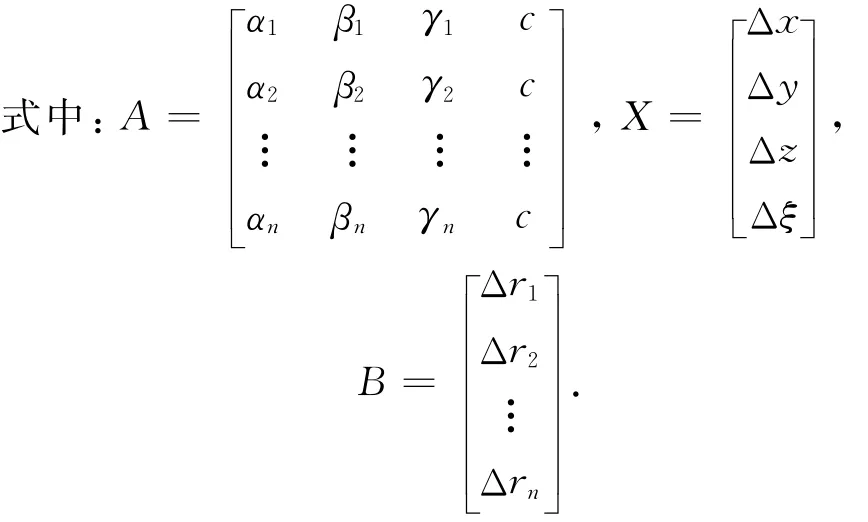
当卫星数目n＞4时，可用最小二乘（ATA）－1ATB求解。根据中心极限定理，假设伪距测量偏差服从高斯分布［9］，因此Δr服从E［Δri］＝0，E［Δri，Δrj］＝0（i≠j），E［Δr2i］＝σ2r。令C＝（ATA）－1，（c1，c2，c3，c4）为矩阵C的4个对角线元素，则Δx可以表示为

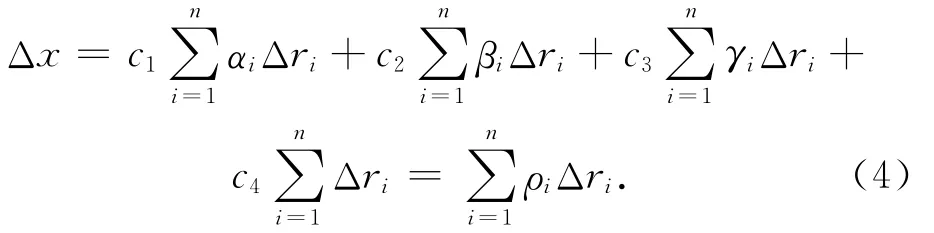
式中，ρi＝c1αi＋c2βi＋c3γi＋c4。

由于Δr服从高斯分布，结合式（4）可得

由上式可以看出，接收机位置x坐标偏差的方差σ2x是伪距测量偏差的方差σ2r和与几何位置相关的量ρi的函数。考虑到σ2r一般为常数，因此σ2x仅为ρi的函数。同理，σ2y和σ2z可以表示为

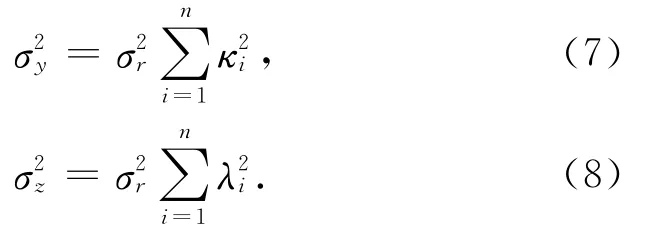
式中，κi和λi的含义类似式（4）中的ρi。

综上，GDOP可以表示为

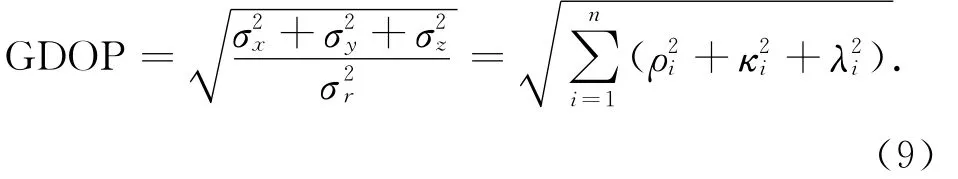
1．2 GDOP与星座几何分布

由上节分析可知，GNSS的定位精度可用公式表示为

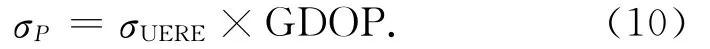
式中：σP为位置精度；σUERE为用户等效距离误差；GDOP为几何精度因子。等效距离误差是根据卫星至接收机路径上各种因素预测的伪距观测值的变化值，GDOP反映卫星的空间几何分布，定义为用户等效距离误差到最终定位误差的放大系数。

设卫星的高度角为α，方位角为θ，卫星数为n，定义系数矩阵

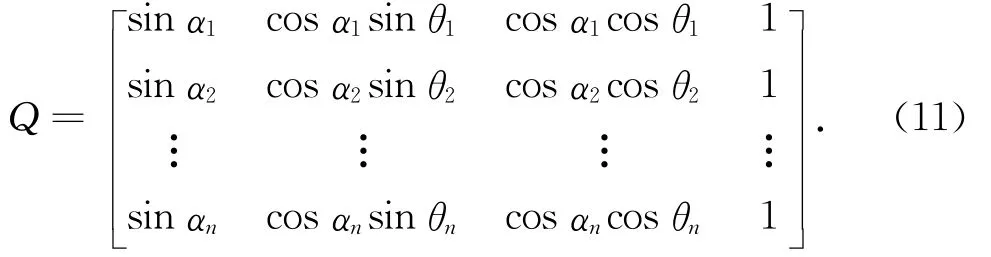
则几何精度因子GDOP可以表示为

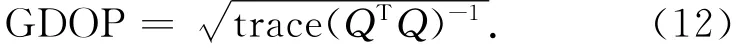
其中，trace为矩阵求迹。由式（11）和式（12）可以看出，GDOP的值仅与卫星的高度角和方位角有关。

目前，GPS、GLONASS和北斗导航卫星系统可观测卫星总数达到70颗（32＋24＋14）。本文采用一台多模接收机在北京地区进行24h连续观测，可见卫星如图1所示。

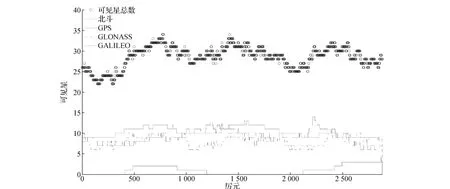
图1　北京地区可见星

由图1可以看出，北京地区24h观测弧段内四系统（北斗、GPS、GLONASS、GALILEO）可见卫星达到22～34颗，可观测的北斗卫星要多于GPS和GLONASS卫星，这是由于北斗导航卫星系统的5 颗GEO卫星（Geostationary Earth Orbit，地球静止轨道卫星）和5颗IGSO卫星（Inclined Geosynchronous Satellite Orbit，倾斜轨道卫星）均位于亚太地区。由于GALILEO只有4颗在轨卫星，因此某些历元观测不到GALILEO卫星。

星历给出的是地固坐标系下的卫星坐标，需要将其转换至站心坐标系中才能进行选星运算。站心坐标系与地固坐标系的关系如图2所示，站心坐标系的原点为测站，测站在椭球体的法线方向为Z轴，测站大地子午线北端与地平面的交线为X轴，测站大地平行圈东端与地平面的交线为Y轴。地固坐标系到站心坐标系的坐标转换方程为

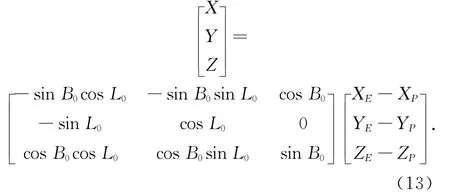
式中，（XPYPZP）和（B0L0）分别为测站地固坐标系中的三维坐标和经纬度。

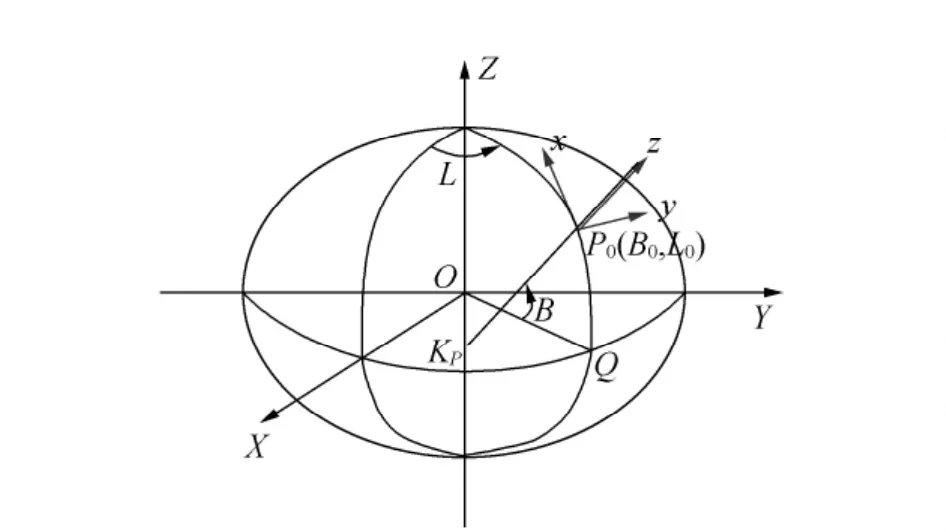
图2　地固坐标系与站心坐标系的关系

2　基于隶属函数的选星法

随着卫星到测站的单位矢量端点所围成的体积V的增大，总体趋势上GDOP值是减小的［10］。因此，对于单系统导航定位最低要求4颗卫星而言，由于正四面体的体积最大，可知1颗卫星在测站头顶，另外3颗卫星在测站与地面相切的平面上的投影互隔120°时具有最小GDOP值。对于由n个星座组成的组合系统而言，为了满足定位求解的需要，至少要选取（n＋3）颗可见星，这是由于不同卫星系统之间存在着系统时差，所以在解算方程中要多引入一个系统间的钟差量。

在卫星导航系统定位解算过程中，总是希望选择GDOP最优的卫星星座。但以最优GDOP为原则进行选星时，因其计算量太大，不能满足实时性的要求。特别是在多星座组合导航情形下，可见卫星数n很大，如果以最优GDOP为原则从中选择m颗卫星，则需要进行Cmn次GDOP求解，其计算量是巨大的，从而占用很长时间，对实时用户而言，这是无法承受的。本文提出的方法，仅需计算几次GDOP值，计算效率大大提高。具体步骤如下：

步骤1：参数设置。根据导航定位的需要及组合星座的个数，设置所需选取的导航定位卫星数目和GDOP的限制要求；为了剔除较低仰角的卫星，还需要设定卫星最低高度角αL；最后根据选星的总数合理确定顶座星和底座星的个数。

步骤2：数据准备。根据卫星星历获取可见星位置，并将其转换到站心坐标系中，获取可见星的高度角α和方位角θ，剔除高度角小于αL的卫星。将可见星高度角由大到小排列，并均匀分成3段，形成高、中、低层卫星。

步骤3：顶座星的选取。以选取2颗星为例，首先在高层卫星中选择高度角最大的卫星作为第1颗星。在选择顶座第2颗星时，需要综合考虑高度角和卫星分布情况，应该在高层中选择高度角尽可能大并与第1颗星分布均匀的卫星。因此，依据模糊数学理论，选择抛物型分布隶属函数，后续的实验结果也表明，抛物型分布隶属函数可以满足选星精度及实时性的要求，抛物型隶属函数分为

降半抛物型分布

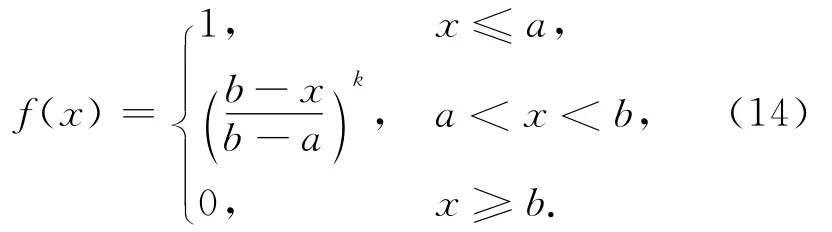
升半抛物线分布

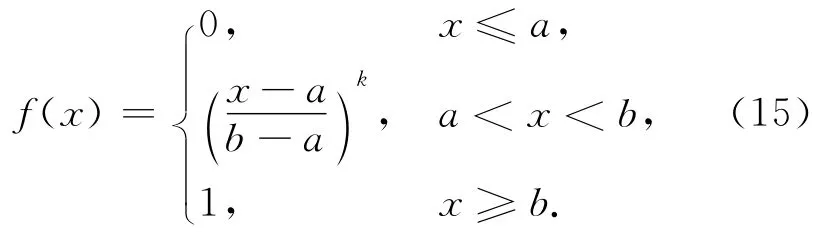
中间抛物型分布

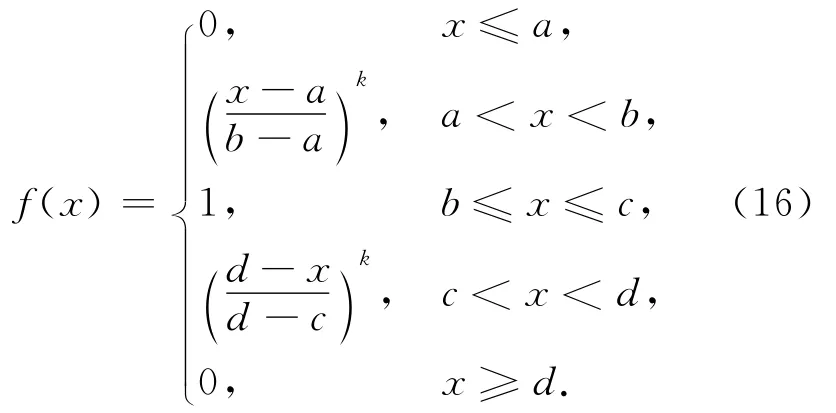
选择高度角隶属函数中最大高度角A的隶属度为1，选择方位角隶属函数中与第1颗星的方位角夹角在（180°－r，180°＋r）的隶属度为1。隶属函数图形如图3所示。

图3　顶座星选取隶属函数

构造函数

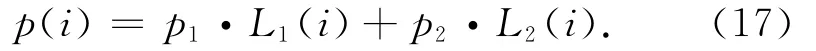
式中：（p1，p2）为高度角与方位角的权重，且p1＋p2＝1；L1（i）和L2（i）分别为第i颗卫星高度角和方位角的隶属度。选取p（i）值最大的卫星作为顶座第2颗卫星。

步骤4：底座星的选取。以选取4颗星为例，底座星应该具有最小的高度角，因此，在中、低层卫星中选择具有最小高度角的卫星作为底座第1颗星。由于底座卫星需要选取4颗，因此，以底座第1颗星的方位角为起点，依次旋转90°、180°和270°并选择高度角隶属函数中最小高度角B的隶属度为1。类似图3，底座星选取的隶属函数如图4所示。

隶属函数构建完成后，根据式（7）选取p（i）值最大的卫星作为下一颗底座卫星。

步骤5：求解GDOP。若GDOP值满足设计要求，则所选卫星为导航定位卫星，完成选星。若GDOP不能满足要求，则在底座卫星中增选一颗与邻近两颗已选卫星方位角相差最大的卫星。

步骤6：再次求解GDOP。若GDOP值满足设计要求，则所选卫星为导航定位卫星，完成选星。若GDOP不能满足要求，则重复步骤4、5。选星流程如图5所示。

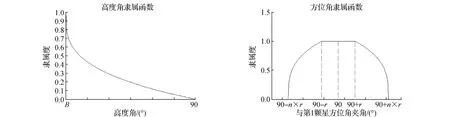
图4　底座星选取隶属函数

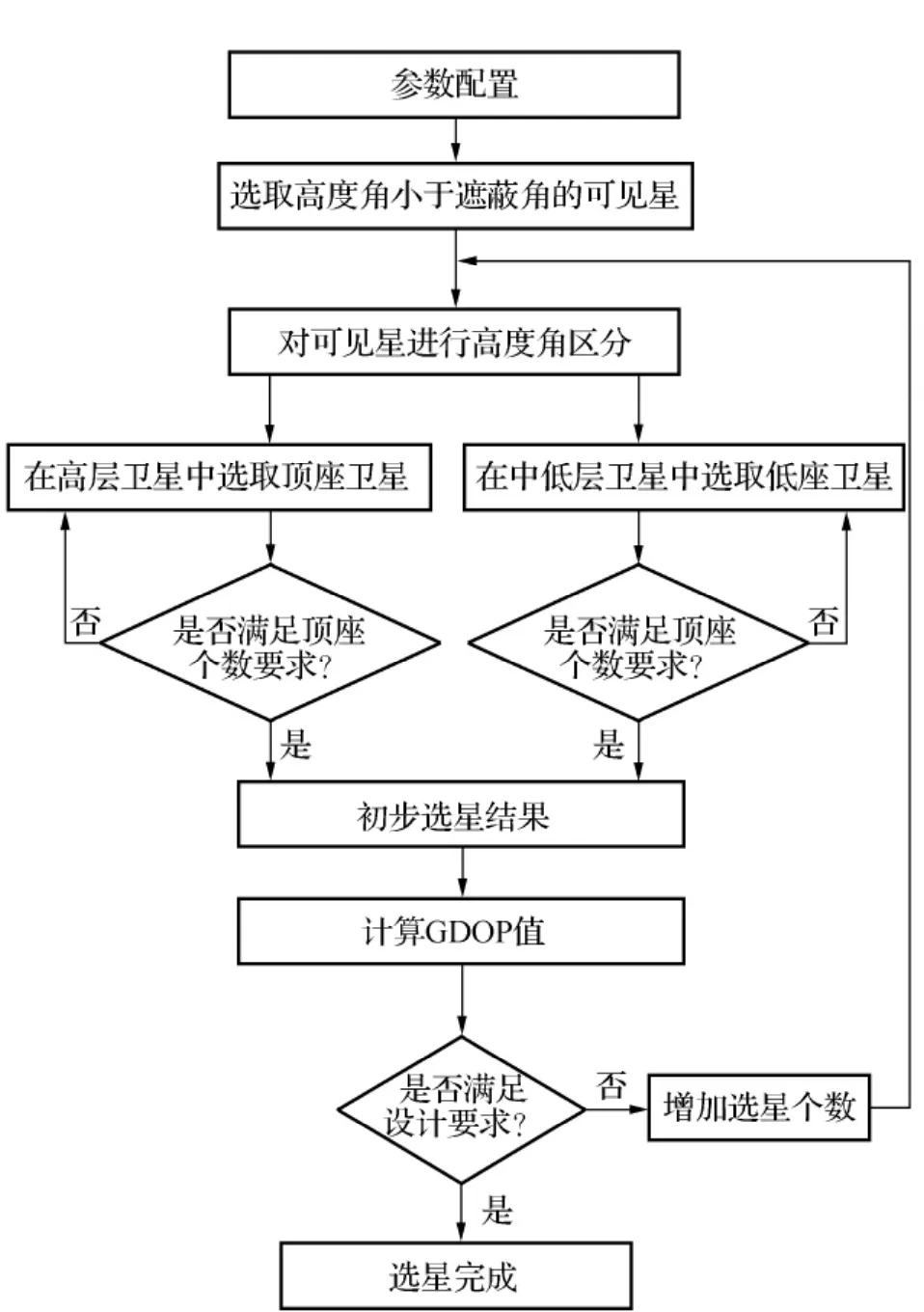
图5　选星流程

3　实验与分析

本次实验采用一台多模接收机在北京地区进行24h连续观测，可见卫星如图1所示，在图中可以看出，北斗、GPS和GLONASS每个历元均可观测到较多卫星，因此在这3个系统中进行选星，最少需要选择6颗卫星，包括2颗顶座星和4颗底座星；设置最低高度角为10°；通常GDOP值应小于6，由于可选卫星较多，本文将最大GDOP值设定为4。选星间隔为5min。按照上述选星方法，选星结果如图6～9所示。

图6　选星前后卫星空视图

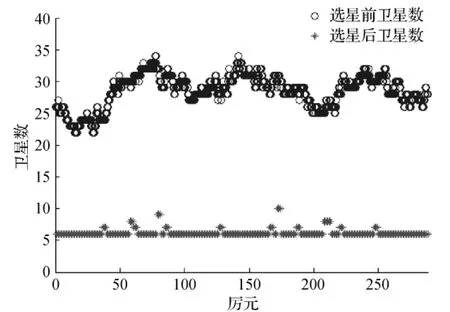
图7　选星前后卫星数对比

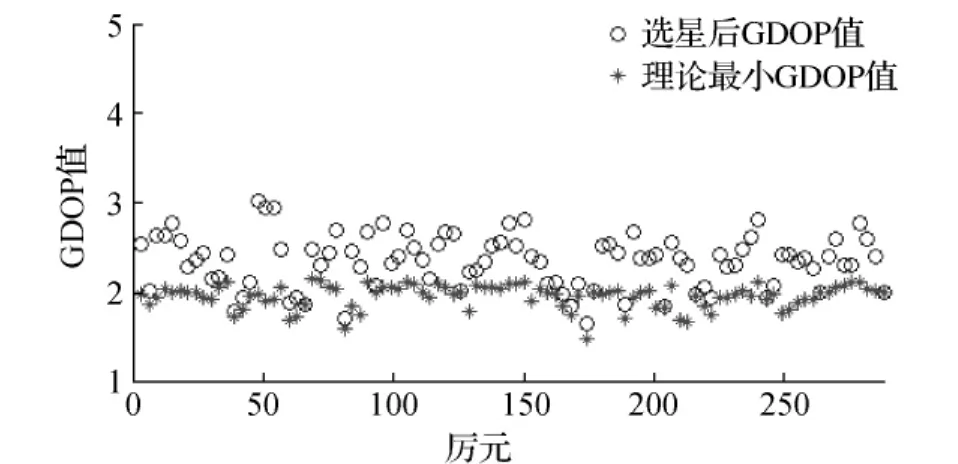
图8　选星后的GDOP值与理论最小GDOP值比较

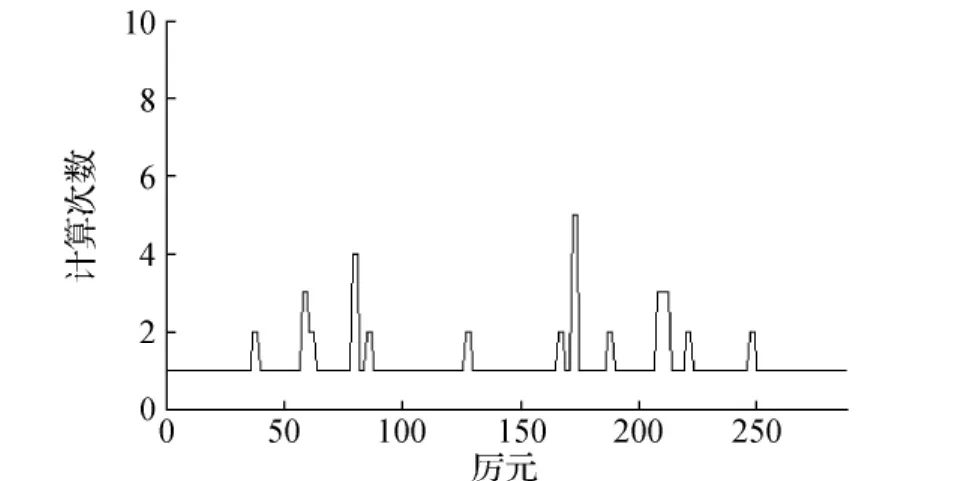
图9　GDOP值计算次数

图6为北京地区2014年第113天UTC时 07：00时刻选星前后卫星空视图。图中，C、G、R分别代表北斗卫星、GPS卫星和GLONASS卫星，选星前，可见星数目较多（34颗），选星后，可见星分布较好，其GDOP值为2．593，满足设计要求。图7为选星前后卫星数对比图，由图中可以看出，选星后用于导航定位的卫星远少于选星前可见卫星数，这将大大降低接收机处理器的负担，有利于快速实时定位。图8为选星后的GDOP值，由图中可以看出选星后大部分时刻GDOP值位于2～3之间，满足设计要求。图9为GDOP值计算次数，24h统计结果显示86．81%时刻仅需求解一次GDOP就可以满足GDOP值小于4的设计要求，98．26%的时刻求解GDOP的次数不超过3次。这表明本文所提出的选星算法可以达到快速选星的目的。

本次实验中，24h观测弧段理论最小GDOP的平均值为1．95，利用本文提出的方法选择6颗星的GDOP平均值为2．34。由式（6）～（9）和式（10）可知，选星会造成约1．2σP的精度损失，这在高精度定位中精度损失是不能接受的，但本文提出的选星方法面向高动态快速定位，损失精度在所难免，而且损失的精度远小于3倍中误差，因此该方法可用作快速导航定位的选星。

4　结 论

1）本文提出的选星算法是以GDOP的限制要求为前提进行选星，最终选择的GDOP值虽然不是最优，但能满足导航定位的需要，并且该算法目标明确，24h统计结果表明，该方法能在不超过3次求解GDOP的情况下，以不小于98%的概率获得GDOP≤4的要求。

2）从计算量来看，最优GDOP法远远大于本文提出的选星算法。若按照传统的最小GDOP法按需要在n颗卫星中选取m颗卫星，需进行Cmn次GDOP值计算，对于多系统组合来说，其卫星总数较多，因而运算量巨大，这对实时用户来说是不能接受的。而本文提出的方法仅检核计算时计算GDOP值，其运算量不足传统最小GDOP法的1%，这为该方法在高动态条件下实时选星提供了保证。

3）本文仅在三系统进行组合导航最少6颗星的情况下进行选星，若是进行接收机完好性和故障检查，需要最少7颗卫星，而排除故障，则需要最少8颗卫星。对于传统最小GDOP法来说，每增加一颗卫星，就会增加其逆矩阵的维数，计算量都会成倍增加。而本文提出的算法仅在一次选星结束后求一次逆矩阵，即使选取较多卫星时也不会明显增加计算量，并且所获得的GDOP值可以满足导航定位的需要，是一种可实时求解的选星算法，也适用于选择较多颗卫星的情况。

4）本文以获得满足设计要求的GDOP而非最优GDOP为前提，以优先考虑卫星方位角分布，同时兼顾卫星高度角为原则，提出了一种新的选星方法，详细讨论了其具体实施步骤，给出了方法流程，探讨了实际应用中相关参数的配置。实验结果表明，该方法能以较少的计算量，快速选择满足GDOP设计要求的卫星，虽然导航定位的精度有所损失，但是仍然在可以接受的范围内，因此本文提出的方法能有效用于多星座卫星导航系统的实时选星求解。

参考文献：

［1］ 王琰，宋力杰，黄令勇．GPS卫星精密定轨中的摄动力分析［J］．测绘工程，2013，22（5）：17－24．

［2］ 杨元喜．北斗卫星导航系统的进展、贡献与挑战［J］．测绘学报，2010，39（1）：1－6．

［3］ 王乐，贾小林，范丽红，等．北斗卫星18参数广播星历拟合中关于调和项的影响分析［J］．测绘工程，2014，23 （1）：40－44．

［4］ 罗小敏，蔡昌盛，潘林，等．利用单频GPS／Galileo组合观测值的导航性能分析［J］．测绘工程，2014，23（9）：22－25．

［5］ 李敏，刘小汇，王瑛，等．新的GPS自适应阵的选星方法［J］．通信学报，2007，28（6）：127－132．

［6］ 任磊，王雪梅．高动态GPS／INS组合导航中一种新的选星算法［J］．计算机测量与控制，2011，19（12）：3096－3101．

［7］ MOSAVI M R．An Efficient Method for Optimum Selection of GPS Satellite Set Using Recurrent Neural Network［A］．IEEE／ASME International Conference on Advanced Intelligent Mechatronics［C］．2009：245－249．

［8］ MISRA P，ENGE P．Global Positioning System Signals Measurement ＆Performance（Second Edition）［M］．Ganga Jamuna Press：2006．

［9］ 程鹏飞．全球卫星导航系统GPS，GLONASS，Galileo及其他系统［M］．北京：测绘出版社，2009．

［10］ESMOND M．Paul A．A Fast Satellite Algorithm for combined GPS and GLONASS receivers［J］．Journal of the Institute of Navigation．2000，47（3）：383－389．

［责任编辑：刘文霞］

A fast satellite selection algorithm for multi－satellite navigation system

MA Hongyang1，CHENG Pengfei2，LI Ran3，HUANG Huadong3

（1．Chinese Academy of Surveying and Mapping，Beijing 100830，China；2．National Surveying and Mapping Product Quality Inspection and Test Center，Beijing 100830，China；3．Shandong University of Science and Technology，Qingdao 266510，China）

Abstract：To resolve the conflict between positioning accuracy and real－time capability when using multisatellite navigation system，a new algorithm for choosing visible satellites is presented．The operation of satellite selection of the proposed method is operated on the premise that the positioning requirement Geometric Dilution of Precision must be met，rather than calculating the minimal GDOP．By utilizing the membership function in the theory of fuzzy，the method is based on the principle of uniform distribution of satellites．The error model of pseudo range measurement is derivated and the relationship between GDOP and measurement error is analyzed．The experimental results which combine Compass，GPS and GLONASS show it can achieve GDOP≤4in no more than 98%within 3GDOP calculations．

Key words：satellite navigation system；satellite selection；membership function；Geometric Dilution of Precision（GDOP）

作者简介：马宏阳（1991－），男，硕士研究生．

基金项目：北斗分析中心资助项目（GFZX0301040308—06）

收稿日期：2014－10－13

中图分类号：P228．4

文献标识码：A

文章编号：1006－7949（2015）10－0059－06