GNSS偏心观测在卫星天线定位定向中的应用

卢 书

（96319部队，广东普宁515347）



GNSS偏心观测在卫星天线定位定向中的应用

卢 书

（96319部队，广东普宁515347）

摘 要：由于现地观测条件限制，GNSS天线无法架设在需要观测的目标点上，无法实现精确对中观测目标所对应的地面点中心，此时就需要进行GNSS偏心观测。文中从解决卫星天线定位定向的工程出发，研究GNSS偏心观测三角形法和经纬仪交会法计算归心元素。依据模拟实测计算结果以及实际卫星天线定位定向的结果，分析了两种方法的优缺点。

关键词：GNSS偏心观测；归心元素计算；三角形法；经纬仪交会；卫星天线定位定向

随着测量技术的快速发展，GNSS（特别是GPS）已广泛应用于大地测量、工程测量、航空摄影测量、工程变形监测等多种学科［1］。

GNSS与经典大地测量相比，其高精度、自动化、高效率等优点突出。但由于某些站址点无法满足GNSS天线的架设要求，往往采用GNSS偏心观测的方法来解决此类问题。虽然使用经典大地测量方法也可解决此类站址坐标的测量，但由于经典大地测量方法自动化程度不高、测量效率较低而不予以采用。GNSS偏心观测的结果必须精确地归算至目标点标石中心，其归算的精度一般不可超过天线安置的对中误差［2］。天线安置误差为TBC软件默认值，不超过0．02m。

1　GNSS偏心观测

1．1 GNSS偏心观测的基本原理

GNSS（GPS）偏心观测与经典大地测量中的偏心观测概念基本一致，但是关于归心元素的测定与归心改正数的计算方法有所不同。如图1所示，GNSS偏心观测时的归心元素是在偏心观测站进行测定的。

Pk点为偏心观测站，P0点为待测站点，则P0

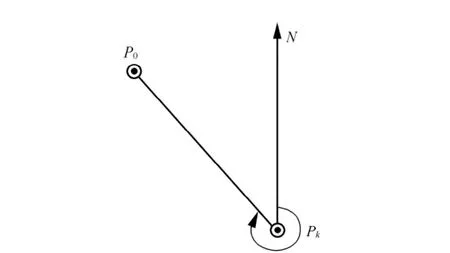
图1　GNSS偏心观测

点在以Pk点为原点的站心坐标系的关系式为

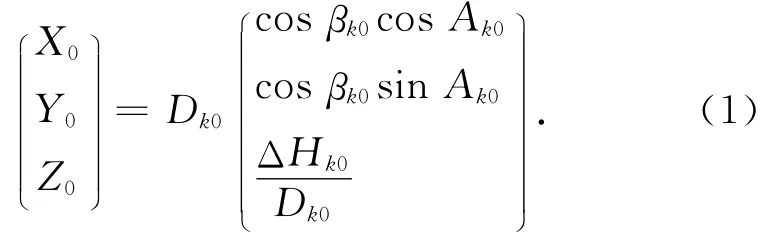
其中：βk0＝arcsin（）；ΔHk0为Pk点与P0点之间的高差；Ak0为Pk点与P0点之间的法截面大地方位角；Ak0为Pk点与P0点之间的斜距。需要指出的是，在偏心观测站Pk点的站心极坐标中，Pk点的极坐标（Dk0，Ak0，ΔHk0）即为偏心观测的归心元素，其中斜距和高差可分别由激光测距仪和精密水准联测（或三角高程）确定。分析式（1），归心元素的测定就是要确定待测站与偏心观测站之间的位置关系。

1．2 归心元素的测定与计算

1．2．1 三角形法

三角形法是GNSS测定归心元素应用比较广泛的简便方法。如图2所示，设P0为GNSS观测点标石中心，P1为GNSS偏心观测点，P2为辅助点（用于辅助测定P1至P0的大地方位角）。

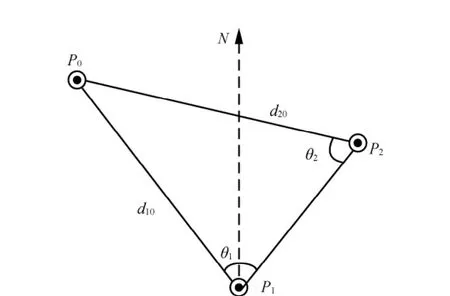
图2　三角形法

在P1点与P2点架设安置GPS接收机，通过相对测量可以获得P1，P2点在WGS－84的空间直角坐标分别为（X1，Y1，Z1），（X2，Y2，Z2），P1至P2的基线向量还可以得到。同时用全站仪可以测出P0P1，P0P2的斜距d10，d20以及高差h1，h2。以P1点为坐标原点，可以求得P2点在以P1点为原点的站心坐标系的站心地平坐标［3］。具体步骤如下：

1）计算P2点在P1点站心坐标系中的坐标。

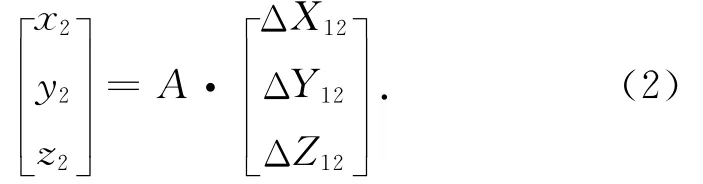
式中，

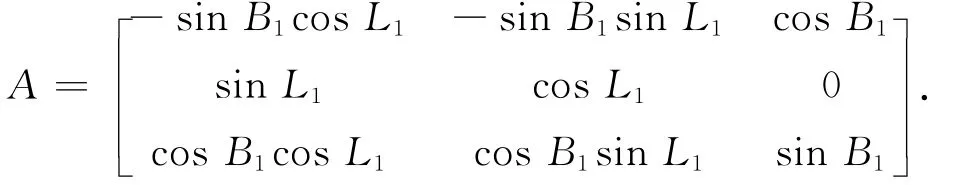
其中：B1，L1为P1点在WGS－84坐标系下的大地纬度、大地经度，P2点至P1点的大地方位角为α12。

2）计算P1P0，P1P2边的法截面大地方位角

当x2＞0，y2＞0时，α12＝α；y2＜0时，α12＝α＋360°；当x2＜0时，α12＝α＋180°；所以α10＝α12＋θ1。

3）计算P0点在P1点站心坐标系的坐标

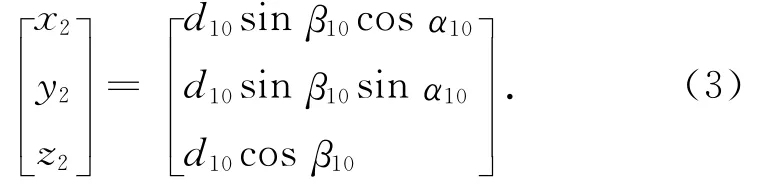
也可以改写为

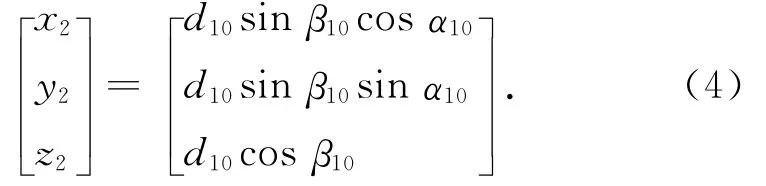
4）计算P0点与P1点之间的坐标差

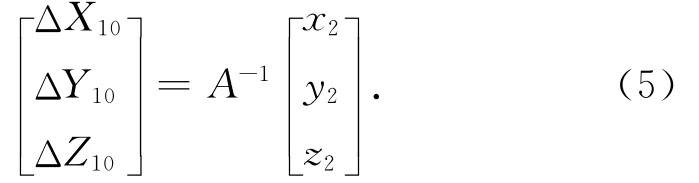
5）根据坐标差即可计算出待测点P0在WGS－84坐标系下的坐标

在三角形△P1P0P2中满足正弦定理

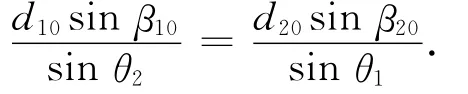
为检验归心元素计算是否正确，可由归心元素（ΔX10，ΔY10，ΔZ10）计算出两点的距离与高精度激光测距仪的测距数据进行对比。

也可通过以P2为站心坐标原点归心计算得到的P0坐标（X02，Y02，Z02）与以P1为站心坐标原点归心计算得到的P0坐标（X01，Y01，Z01）的坐标分量之差的平方和。

1．2．2 经纬仪交会法

经纬仪交会法是指通过使用两台定位定向的全站仪，通过空间前方角度交会的方法得到待测点的坐标［5］。在P1，P2两点分别架设两台高精度的全站仪TM5100A，以P1，P2两点连线（可通过高精度测距或者高精度GNSS控制网结果获得）作为距离基准，并通过P1，P2两已知点对系统进行定向，建立以P1点为系统原点的经纬仪测量系统［6］。利用交会测量的方式得到控制网中公共点的坐标（用以求解经纬仪测量系统坐标系与WGS－84坐标系的转换参数）以及f1、f2的三维坐标，采用公共点转换的方法将f1、f2坐标转换至WGS－84坐标系下。

如图3所示，共有N－1个辅助点Pi（i＝2，3，…，N）。在辅助点Pi与P1点架设经纬仪测量系统，交会测量得到以P1为测站原点的N－1组P0点的坐标（X0i，Y0i，Z0i）。

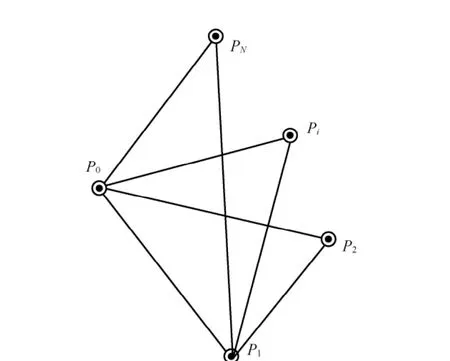
图3　经纬仪交会法

取N－1组坐标分量的中数分别为

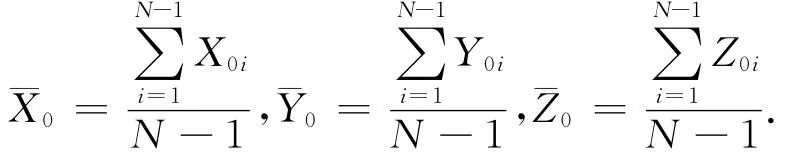
则

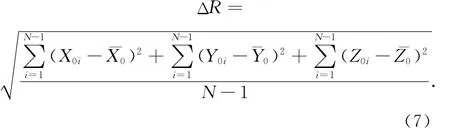
对比三角形法的归心计算精度要求，经纬仪交会法得到的归心计算的结果也必须满足ΔR＜4mm（重复精度要求）。

2　卫星天线定位定向

如图4所示，模拟某一遥感卫星天线定向工程，O点为遥感卫星天线的相位中心，f1、f2为遥感卫星天线的两个定向点。要实现遥感卫星天线定位定向，需要测量得到O点的大地坐标，f1、f2的大地坐标，O点至f1与O点至f2的大地方位角以及两边的夹角。由于现地条件限制，以及卫星天线定向要求，定向点f1、f2无法直接架设GPS接收机，需要进行GPS偏心观测。根据测量任务布设如图4所示的控制网。实际模拟实验中f1与f2均架设了GPS天线，用以确定三角形法与经纬仪交会法偏心观测的精度。

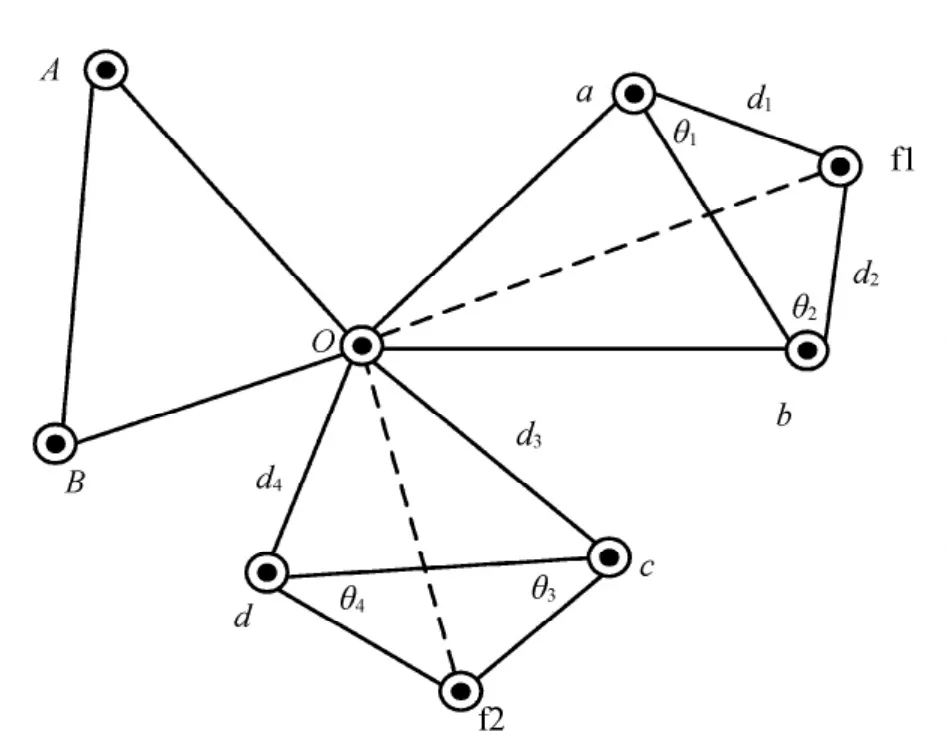
图4　卫星天线定向控制网

具体测量方案是，按照GNSSⅢ级测量的技术要求在O点、A点、B点架设GPS，解算出O点的大地坐标；按照Ⅳ级测量的技术要求在O点、a点、b点、c点、d点架设GPS，解算出以上5点的大地坐标，见表1。

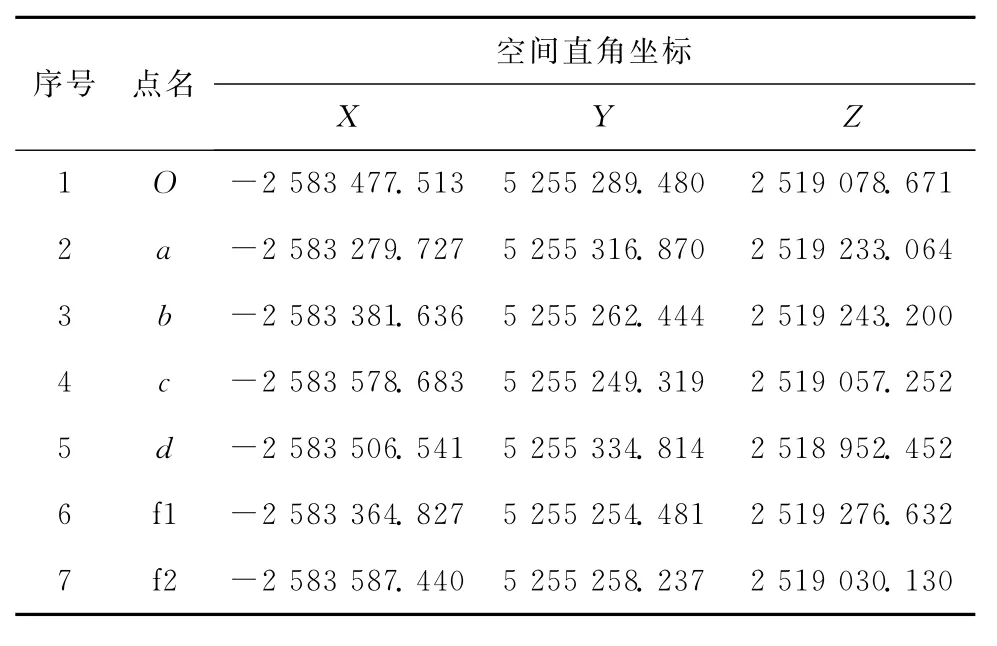
表1　控制网点空间直角坐标　m

按照三角形法做归心计算时，分别以a点为偏心观测站，以b点为辅助点计算f1点的归心元素得到f1点的归心元素，从而得到f1点的空间直角坐标；以c点为偏心观测站，以d点为辅助点计算f2点的归心元素，从而得到f2点的空间直角坐标，具体结果见表2。

表2　三角形法偏心计算结果　m

按照经纬仪交会法的方案，在a、b点架设全站仪交会测量f1的三维坐标，在c、d点架设全站仪交会测量f2的三维坐标，然后公共点转换至WGS－84坐标系下，具体结果见表3。两种方法对比见表4。

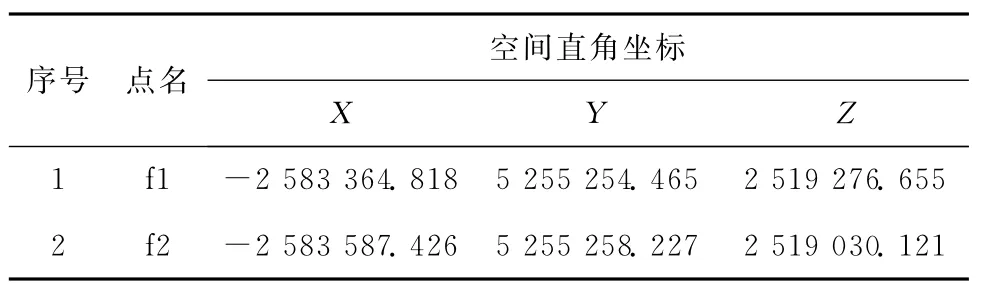
表3　经纬仪交会法偏心计算结果　m

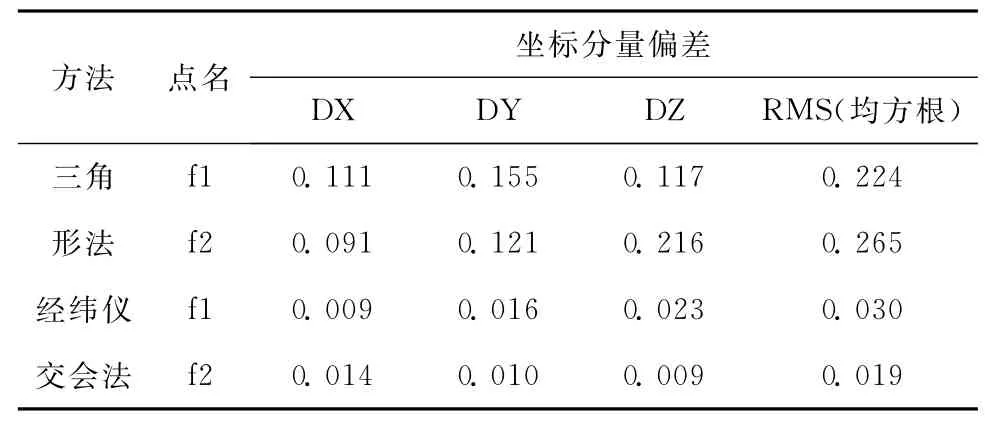
表4　两种方法与控制网点的差值对比　m

以表1模拟的控制网数据视为“真值”，将表2、表3的偏心计算结果与表1的“真值”进行对比，可知三角形法计算偏心元素得到的点位坐标分量相差在分米级，而经纬仪交会法计算偏心元素得到的点位坐标分量相差在厘米级（满足归算精度不低于天线安置误差的要求），交会测量的结果更接近“真值”，显然经纬仪交会法偏心观测的精度要明显优于三角形法。

从两组实测数据用于卫星天线定位定向的结果来看，方位角精度越高遥感卫星天线跟踪时搜索的卫星越多、信号越好，因此经纬仪交会法无论是精度还是测量效果来看都优于三角形法。

3　结 论

随着GNSS系统在测绘领域的广泛应用，GNSS测量的高效率、高精度优势得到了充分发挥，GNSS系统展现了其广泛应用于工程测量的前景。GNSS偏心观测使得GNSS在工程测量中的应用进一步拓宽。通过本文的应用实例研究，验证了GNSS偏心观测三角形法和经纬仪交会法均可应用于卫星天线定位定向工程，可以得到下述几方面的结论：

1）GNSS偏心观测的实际应用时，可根据实际应用工程所需的测量精度和测量效率选择可行的GNSS偏心观测方法。

2）从偏心计算的公式可以看出，归心元素的测定精度与偏心观测站坐标精度以及偏心距有关。

3）在偏心观测站的坐标精度相同的情况下，经纬仪交会法偏心观测的精度比三角形法偏心观测精度要高一个数量级。

4）在进行上述模拟实验数据计算时发现，无论三角形法或经纬仪交会法都应顾及偏心三角形的形状，以达到提高归心计算精度的目的。下步将对三角形法的夹角和交会法的交会角的大小对偏心观测精度的影响以及两种方法本身的重复精度进行研究。

参考文献：

［1］ 曾云，张予杰，高西峰．GPS偏心观测及其精度分析［J］．全球定位系统，2002（6）：3－7．

［2］ 万军，王丽华，程绪红．直线型GPS偏心观测法［J］．港口科技，2007（9）：26－28．

［3］ 周林根，张发栋．GPS归心元素精度初探［J］．港工勘察，1999（40）：8－10．

［4］ 国家测绘局测绘标准化研究所，国家测绘局第一大地测量队，国家基础地理信息中心．GB／T 18314－2009全球定位系统（GPS）测量规范［S］．北京：中国标准出版社，2009．

［5］ 李广云，李宗春．工业测量系统原理与应用［M］．北京：测绘出版社，2010．

［6］ 卢书，李宗春．高铁轨道板快速检测方法研究［J］．测绘工程，2012，21（6）：56－59．

［责任编辑：刘文霞］

Application of GNSS eccentric observation to satellite antenna positioning and orientation

LU Shu

（Troops 96139，Puning 515347，China）

Abstract：Due to the restriction of field observation conditions，GNSS antenna cannot be set up on the target point which needs to be observed，and it is impossible to implement the precise center of ground points in the corresponding observation targets．At this moment，GNSS eccentric observation is necessary．This paper，starting from the solution of antenna positioning and orientation，studies the GNSS triangle method and the theodolite intersection method to calculate the elements of center．And also，this paper analyses the advantages and disadvantages of this two methods according to the simulated calculation results and the actual results of satellite antenna positioning and orientation．

Key words：GNSS eccentric observation；elements of centering calculation；triangle method；theodolite intersection method；satellite antenna positioningand orientation

作者简介：卢 书（1984－），男，硕士研究生．

收稿日期：2014－12－03

中图分类号：P228

文献标识码：A

文章编号：1006－7949（2016）01－0065－04