回归－Elman网络在矿坝变形预测中的应用

王祖顺，韩吉德，王春青

（青海省第二测绘院，青海西宁810001）



回归－Elman网络在矿坝变形预测中的应用

王祖顺，韩吉德，王春青

（青海省第二测绘院，青海西宁810001）

摘 要：金矿开展矿坝的变形监测工作，引入多层递阶回归分析模型，有较高的预测精度，但方法较繁琐，计算较复杂。由于变形数据可分离成趋势项与随机项，趋势项可用多元线性回归良好地拟合；随机项的预测，文中采用Elman网络建模计算，最后利用矿坝的实测高程位移数据进行验证，并与多层递阶回归进行比较。结果表明：回归－Elman网络模型比多层递阶回归的预测精度更高，效果更好，且方法简洁实用性强。

关键词：Elman神经网络；回归分析；变形预测；多层递阶回归；组合模型

回归分析模型、时间序列分析模型、人工神经网络模型等，是对变形数据进行预测预报的多种方法，是测绘人员长期地研究相关课题而相继提出的［1］。然而每种模型都有一定的局限性，需满足一定的适用条件。变形体变形机理多样且复杂，结合多学科知识来逼近模拟变形规律是未来研究趋势之一。

形变序列往往既具有确定的趋势项，又具有不确定的随机项。趋势项可以由回归分析较好地拟合，但是随机项，需要进一步处理［2］。文献［3］采取的是多层递阶回归，方法繁琐，且其回归分析的参数并不固定，随时间而改变，计算复杂。而神经网络能够自学习自适应与信息综合，不仅能够运算数值数据，对抽象的问题或未知的系统也能处理［1］。

张文博［4］等将BP神经网络应用于建筑物沉降预测。BP神经网络具有3层的网络结构［5］。它是非线性、自适应处理系统，可以通过自学来逼近输入输出之间的非线性映射关系。预测速度快，容错能力和抗干扰能力强。但是网络信息只能向前单方向流动。学者Elman等提出Elman神经网络模型。其内部的神经元不仅有前馈连接还有反馈连接，是具有记忆的功能动态神经网络。能够更生动更直接地反映系统的动态特性［6］。故本文提出用Elman神经网络来预测随机项。

因此，本文结合回归分析和Elman网络，尝试用回归分析来拟合形变序列里的趋势项并用Elman神经网络来预测随机项，并通过具体算例来加以实现。

1　多元线性回归分析

对于大坝监测点高程变化的线性系统，设系统有n个影响因子μ1、μ2……μn。沉降拟合值为，则多元线性回归分析的数学模型为

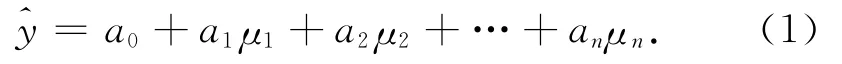
其中a0，a1……an为回归系数。

进行多元回归拟合之后，将实测值与回归拟合值作差，则得到一组残差序列。该残差序列即是随机项。有很多因素影响监测点残差序列的变化，且这些因素同样也是不可准确预知未来值的［10］。但是观测点的时间序列数据内暗含了这些因素造成的影响。故可采用神经网络模型来预测这些监测点的时间序列数据。对随机项用Elman网络建模后，预测出未来的残差值。然后将预测的残差值与回归分析的预测值相加，即得到最终的组合模型的预测值。

2　Elman网络模型介绍

Elman神经网络［7］与前馈神经网络的区别在于增加了反馈通路，是一种动态的非线性模型。陈幸琼等［8］认为，引入反馈通路使得网络能够更有效地综合处理时间序列信息，可将某些神经元的输出经过延时之后反馈到其它神经元或自身，具有适应时变特性的能力。邱峻等［9］认为，Elman神经网络在惯性输入输出数据的处理方面具有无法比拟的优势，从而广泛应用于时间序列预测等方面。不同于与BP神经网络经典的三层结构，Elman神经网络由输入层、隐藏层、关联层、输出层共4层组成，见图1。

其中输入层、隐藏层和输出层的作用与前馈神经网络相似。而关联层的作用在于让当前和以前的输入层数据皆对输出层有影响。此特性有利于时间序列的预测。

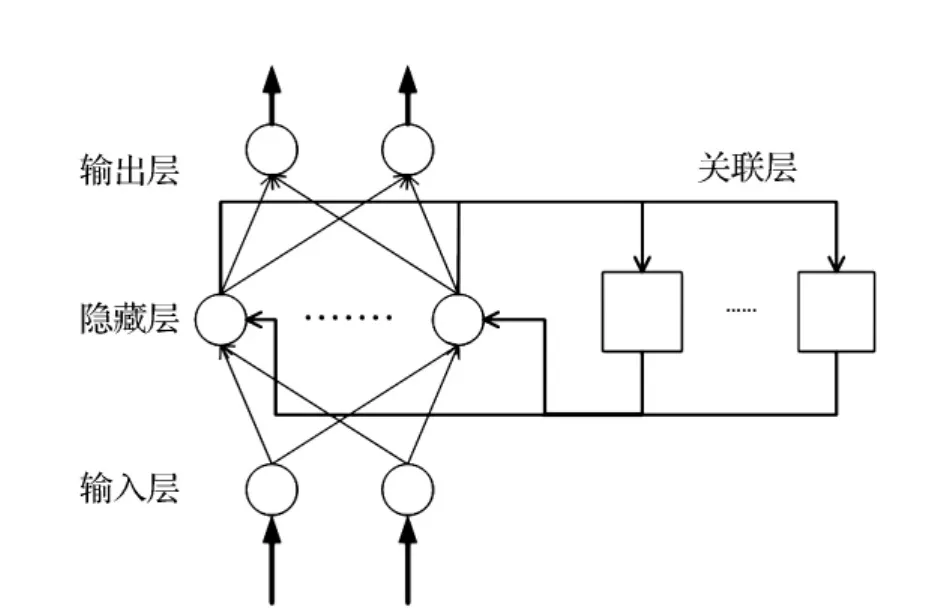
图1　Elman神经网络结构

简述Elman网络的算法［9］如下。Elman网络的非线性状态空间表达式为

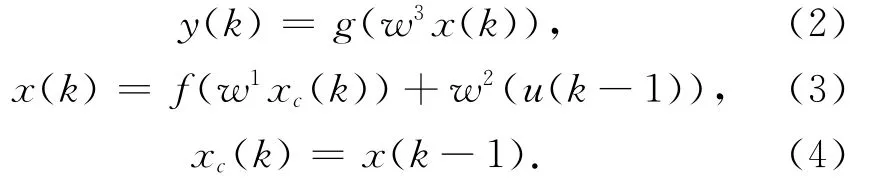
其中，y为输出结点向量，x为n维中间层结点单元向量，u为r维输入向量，xc为n维反馈状态向量，w3为中间层到输出层连接权值，w2为输入层到中间层连接权值，w1为承接层到中间层的连接权值，g函数为输出神经元的传递函数，是中间层输出的线性组合。f函数为中间层神经元的传递函数，常采用Sigmoid函数。

3　工程应用

本实验数据采用文献［3］中提供的算例。某金矿开展了矿坝的移动与变形监测工作。从1995年5月开始平均每月监测一次下沉值。根据历史经验，坝内所蓄物质的施压μ1（k）及温度μ2（k）是影响矿坝变形的主要因素。用y（k）表示矿坝的移动值，其中k为离散的流动时间（月）。原始数据及影响因子数据如表1。

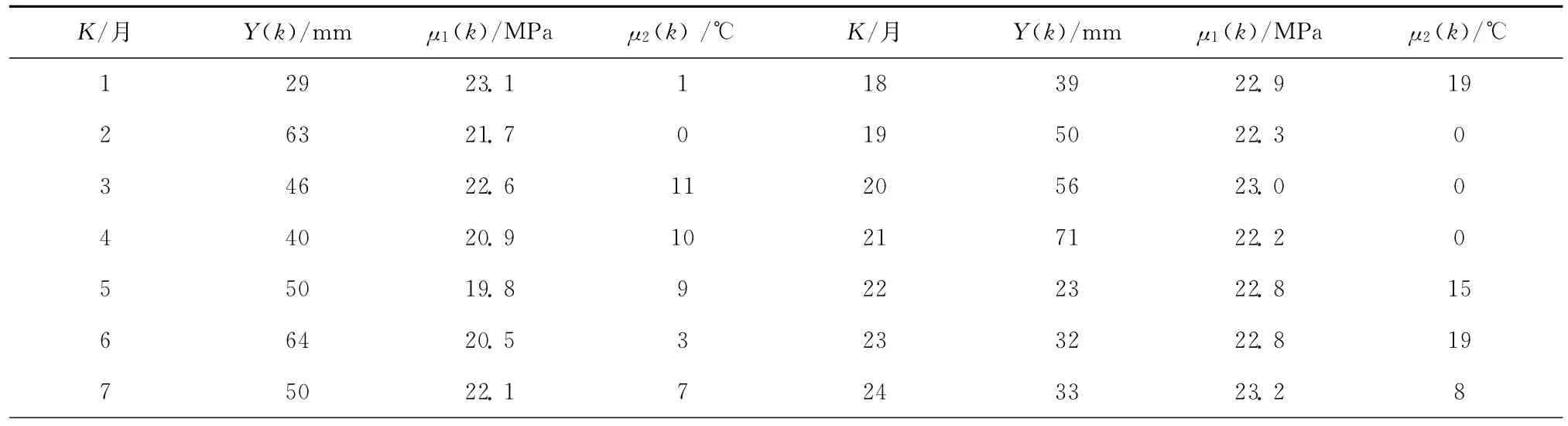
表1　矿坝下沉值与影响因素

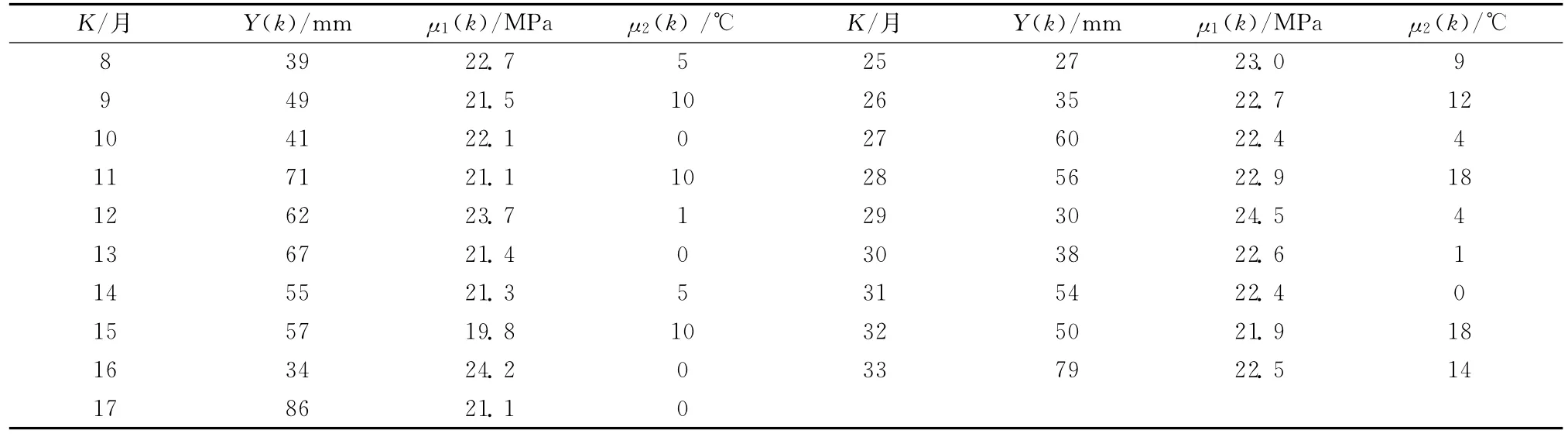
续表1

现由监测到的33次尾坝下沉值，取其前29次下沉值进行建模，并预测出未来4期的数据。图2是前29期的监测值变化曲线。

图2　前29期监测数据

3．1 多元线性回归分析

根据实测数据，进行多元线性回归分析，建立回归方程为：

画出多元回归分析的拟合值，如图3所示。

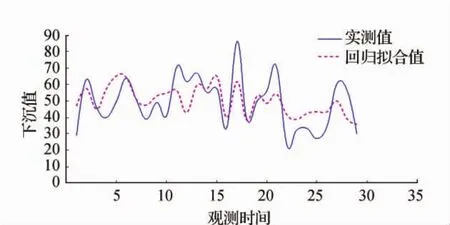
图3　回归模型拟合值

将原始观测值与回归分析的拟合值作差，得到残差序列。如图4所示。

3．2 Elman网络预测残差序列

牛家洋等［10］认为，用人工神经网络模型来预测残差序列的方法，就是将残差序列分为许多组一定长度的样本作为网络的输入，每组样本都将对应1个或多个未来的预测数据，未来的预测值即作为网络的输出。训练网络，利用训练集中的样本对各个神经元的连接进行权重调整，使预测值尽可能逼近期待值，符合精度要求。训练完成后，网络即可用于残差序列的预测。具体步骤如下。

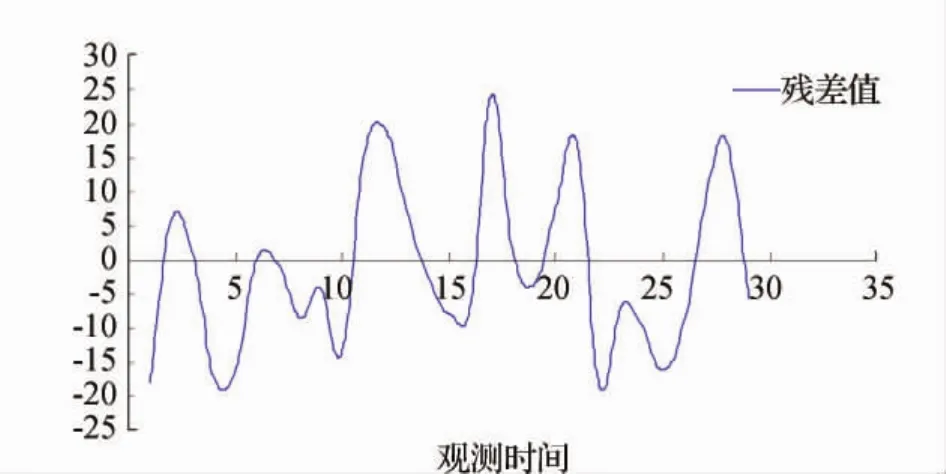
图4　残差值

3．2．1 归一化

数据归一化是把最小的序列值映射为0，最大的序列值映射为1。其余数据依次按照其值的大小按公式映射到［0，1］这个区间。归一化公式如下：

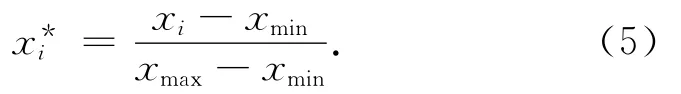
进行归一化避免了因为某些变化范围广的数据在数值上相差过大而造成大数据淹没小数据的问题，将样本数据统一映射到一个符合激活函数要求的区间之内。

3．2．2 确定时间序列的长度

在预测模型中网络输入层的节点数即为时间序列每组样本的长度p。通常将时序数据的变动周期作为步长值。时序数据的变动周期值根据自相关系数来确定。设一个含有n个数据的时间序列｛xi｝，其滞后k步的自相关系数为r（k）：

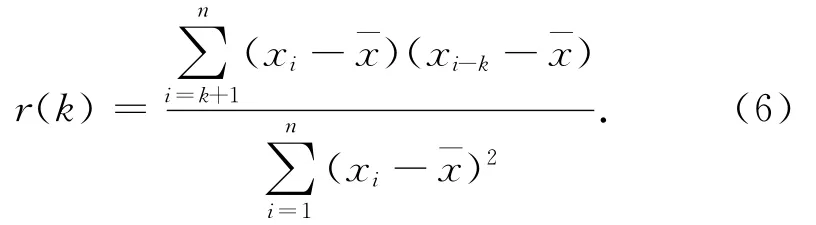
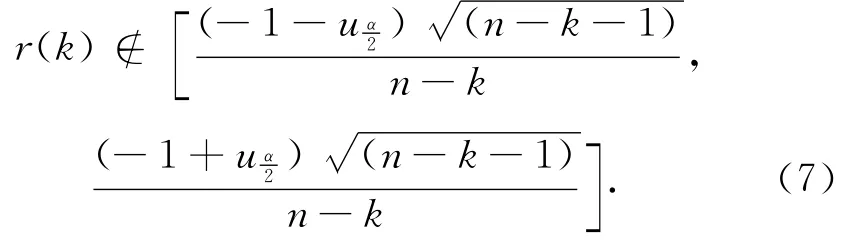
当自相关系数为式（7）时［11］，推断时序延迟k步相关性显著，否则不显著。通常选取最大相关性对应的k作为每组样本的长度p。

3．2．3 网络建模

在Matlab中使用newelm的命令来建立Elamn神经网络。通过反复调试，设置隐含层节点数为10，隐藏层传递函数为tansig函数，输出层激活函数为purelin函数，训练函数选为trainlm函数，并对网络进行训练。

经过上述数据集的训练最终得到Elman网络的预测模型。利用模型得到后4个时间段的预测结果。并将预测结果与多层阶梯回归法做比较。如表2所示。

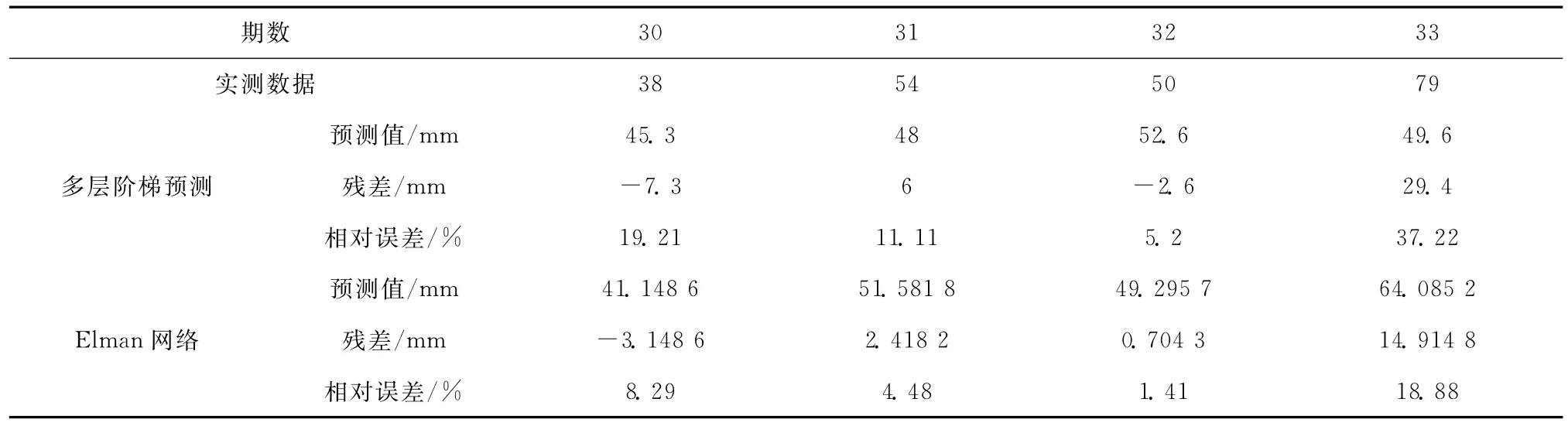
表2　预测结果比较

由上述对比分析结果可以看出，总体上Elman网络在有限次预测内有更好的效果，预测精度普遍提高。

分别计算小波神经网络和Elman神经网络模型预测结果的中误差。

多层阶梯预测结果的中误差为

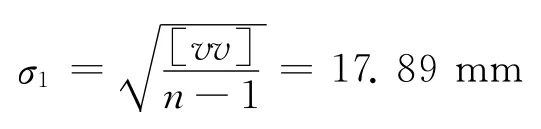
Elman网络预测结果的中误差为

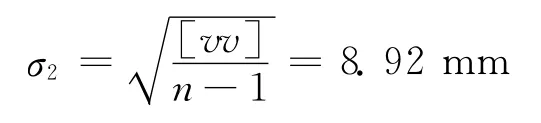
由于σ2＜σ1，故同样证明了Elman网络模型用于变形预测的有效性，可见该模型具有良好的短期预报效果。

4　结 语

回归分析可以很好描述历史数据的趋势项。而Elman网络属于典型的动态神经网络。采用的是动态的建模方法，能够更生动直接地反映出残差的动态特性，使得变形建模能因观测时序数据的更新而更新，并作出相应时序值的预报。所以组合模型预测精度更高、收敛速率更快、效果更好。因此回归分析与Elman网络组合模型适用于变形监测数据的预测，实用价值较好。

参考文献：

［1］ 潘国荣，谷川．变形监测数据的小波神经网络预测方法［J］．大地测量与地球动力学，2007，27（4）：47－50．

［2］ 吴益平，滕伟福，李亚伟．灰色–神经网络模型在滑坡变形预测中的应用［J］．岩石力学与工程学报，2007，26 （3）：632－637．

［3］ 栾元重，吕法奎，班训海．动态变形观测与预报［M］．北京：中国农业科学技术出版社，2007．217－224．

［4］ 张文博，郭云开．基于BP神经网络的建筑物沉降预测模型研究［J］．测绘工程，2013．22（2）：52－56．

［5］ ANDERSON J A．Introduction to Neural Networks ［M］．Cambridge，MA：MIT Press，1995．

［6］ 朱群雄，孙锋．RNN神经网络的应用研究［J］．北京化工大学学报．1998，25（1）：86－90．

［7］ Elman J．Finding structure in time［J］．Cognitive science，1990，14（2）：179－211．

［8］ 陈幸琼，邓长虹，潘章达，等．基于RBF循环神经网络的电力系统负荷建模［J］．电网技术，2007，31（17）：56－59．

［9］ 邱峻，张瑞林．基于遗传算法的循环神经网络在销售预测中的应用［J］．浙江理工大学报，2007．5（3）：266－270．

［10］牛家洋，王洪国，邵增珍．BP人工神经网络算法在鸟情时间序列预测的应用［J］．信息技术与信息化，2013 （3）：93－97．

［11］许国根，贾瑛．模式识别与智能计算的MATLAB实现［M］．北京：北京航空航天大学出版社，2012．

［12］张拯，张献州．时间序列协整关系及其在变形分析中的应用研究［J］．测绘工程，2015，24（9）：53－59．

［13］郇小龙，甄宗坤．基于自回归分布滞后模型的地面沉降预测［J］．测绘工程，2015，24（9）：59－61．

［14］任远军，李龙，石宁，等．改进的GM（1，1）模型在大坝变形预测中的应用［J］．测绘工程，2015，24（6）：61－64．

［责任编辑：王文福］

Application of regression－Elman network model to the dam deformation forcasting

WANG Zushun，HAN Jide，WANG Chunqing

（Second Surveying and Mapping Institute of Qinghai Province，Xi’ning 810001，China）

Abstract：A deformation monitoring for a gold mine is conducted in Shangdong using multi－layered hierarchical regression analysis．A good prediction accuracy is obtained，but the method is complicated in calculation．The deformation monitoring data can be seperated into trend values and random values．Regression method can predict trend values well．To predict the random value，this paper has introduced Elman neural network．The actual monitoring data for elevation displacement variation of mine dam is used for model verification．The prediction result is compared with multi－level recursive regression．It is concluded that better accuracy of prediction can be obtained through the regression－Elman network model and this method is concise and practical．

Key words：Elman neural network；regression；deformation prediction；multi－level recursive regression； combined model

作者简介：王祖顺（1978－），男，工程师．

收稿日期：2014－06－03；修回日期：2015－09－30

中图分类号：TU196＋．1

文献标识码：A

文章编号：1006－7949（2016）01－0039－04