范例多用转化 解题彰显才华——以“复习分数应用题”教学为例谈转化思想的重要性

浙江杭州市萧山区临浦镇第二小学（311251）任灿成



范例多用转化解题彰显才华——以“复习分数应用题”教学为例谈转化思想的重要性

浙江杭州市萧山区临浦镇第二小学（311251）任灿成

［摘要］解答稍有难度的分数、百分数应用题，很多学生都感到棘手。为改变常规的解题教学方法，可尝试把转化思想放在解题教学的首位，当学生解题迷茫时，启发他们通过转化叙述方式、转化数量关系、转化设值方法、转化图表呈示等策略，把转化已知条件和问题或转化另一种思维方法作为解题的首选，这样可使解决问题的方法更加明确，解题思路更为简捷。

［关键词］转化思想范例分数应用题百分数应用题

科学哲学家库思认为：“学生正是通过范例、习题等活动来掌握一门科学知识及其方法。没有范例，科学知识就不能清楚地表达出来，也无法为人们所掌握；没有范例，人们就无法按照该门科学的要求去解决任何问题，数学也不例外。”由此可见，数学课堂中，教师在选择范例进行解题教学时，应当注重剖析转化的多样化途径，分析典型的转化思路，提高学生解决问题的能力。

解答分数、百分数应用题，不能不说是小学阶段应用题教学的一个难点，特别是在总复习阶段，稍有难度的问题，大部分学生在解答时均感到棘手。为改变常规的解题教学方法，我尝试把转化思想放在解题教学的首位，在学生解题迷茫时，启发他们不妨把转化已知条件和问题或转化另一种思维方法作为解题的首选，这样可使解决问题的方法更加明确，解题思路更为简捷。

一、转化叙述方式，明白“1”的转换

在一些分数应用题中，其单位“1”的量不是统一的，很难找到“量”与之对应的“率”（或比较量）。如果能巧妙地转化题目条件中关键的叙述方式，往往可以比较容易地找出解题的路径。

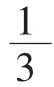
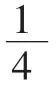
二、转化数量关系，明确“量”的变换

在范例解题教学过程中，我发现大部分学生顺着已知条件能很快找出问题之间的数量关系，但有部分学生理不出头绪，找不到解决问题的“切口”。所以，教师可以引导学生转化已知条件与所求问题的数量关系来求解。

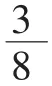
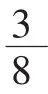
三、转化设值方法，明晰虚实的替换

有些分数应用题比较复杂，而且具体数量比较少，这时我们可以实就虚，假设一些具体数量，为解题搭桥铺路，能够达到化繁为简的效果。

例学校买来故事书的本书是文艺书的75%，已知故事书每本10元，而文艺书的总价是故事书的80%，文艺书每本多少元？

分析：题目中只有“故事书每本10元”这样一个具体数量，很多学生在解题时都认为条件不足，使思维陷入困境。其实，教师不妨引导学生假设文艺书买了80本，则可以求出故事书买了80×75%＝60（本），那么故事书的总价为10×60＝600（元），于是可知文艺书的总价为600×80%＝480（元），即文艺书每本为480÷80＝6（元）。

四、转化图表呈示，明了数形的代换

在实践中，有的题目的条件、问题或数量关系可以转化为图示或表格，这样解决问题更为直截了当。

1．图示法

例容器中有某种酒精含量的酒精溶液，加入一杯水后酒精含量降为25%，再加入一杯纯酒精后酒精含量升为40%。那么，原来容器中酒精溶液的酒精含量是多少？

分析：如下图（△表示纯酒精，○表示水）所示，把加完水和酒精后的酒精溶液分为5份，因为酒精含量是40%，所以其中有2份纯酒精、3份水（如图①）；加入纯酒精前酒精含量为25%，即纯酒精与水之比是1∶3，因此应该是1个△和3个○（如图②）；推知加入的一杯纯酒精相当于1个△，则一杯水是1个○，原来容器中有1个△和2个○（如图③），即酒精含量为1÷（2＋1）≈33．3%。

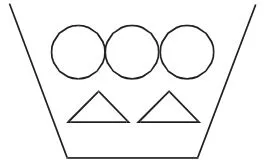
图①

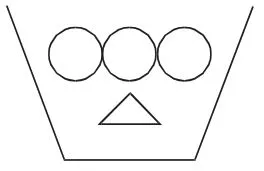
图②

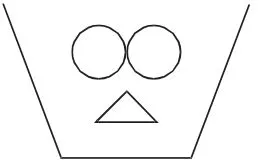
图③

2．画表法

例一只杯子装满了牛奶，明明第一次倒了整杯的一半，然后加满了水，第二次又倒了整杯的一半，然后又加满了水……以此类推，求第四次倒后杯中还剩牛奶几分之几，还剩水几分之几？倒n次后杯中还剩牛奶几分之几，还剩水几分之几？

分析：将每一次倒后杯中剩下的牛奶和杯中的水列入下表，从表中可以得出规律。

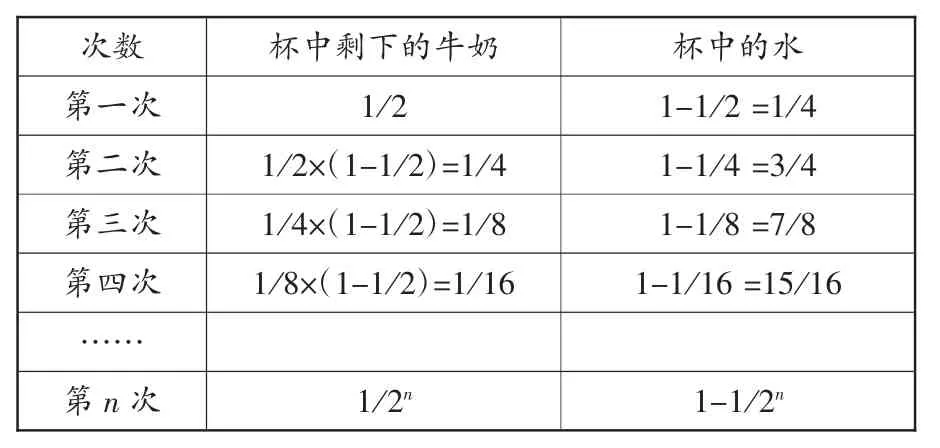
次数　杯中剩下的牛奶　杯中的水第一次　1／2　1－1／2＝1／4第二次　1／2×（1－1／2）＝1／4　1－1／4＝3／4第三次　1／4×（1－1／2）＝1／8　1－1／8＝7／8第四次　1／8×（1－1／2）＝1／16　 1－1／16＝15／16……第n次　1／2n　1－1／2n

教学感悟：

以上四种转化的范例训练，不仅与学生的知识技能有关，更对学生渗透了转化思想，使学生掌握或获得解题所需的方法。解题能力的训练能指导学生正确理解问题的背景，学会分析相关信息并能进行提炼、加工，找出它们之间可以转化的数量关系，如把日常语言转化为数学语言、把数量关系转化为图式关系、把隐蔽关系转化为明朗关系、把繁杂关系转化为简单关系、把未知关系转化为已知关系……

谁也无法教会学生解答所有题目的方法，但通过范例的多样化学习，引导学生从有限的题目中领悟那种解无数道题目的转化机智，使学生的思维真正得到发展，从而提高解题教学的质量，这才是我们解题教学需要追求的目标。

（责编蓝天）

［中图分类号］G623.5

［文献标识码］A

［文章编号］1007-9068（2016）01-034