容量约束的自组织增量联想记忆模型*

孙　桃，谢振平，王士同，刘　渊江南大学数字媒体学院，江苏无锡214122

* The National Natural Science Foundation of China under Grant No. 61272210 (国家自然科学基金); the Natural Science Foundation of Jiangsu Province under Grant Nos. BK20130161, BK2011003 (江苏省自然科学基金).

Received 2015-03,Accepted 2015-05.

CNKI网络优先出版：2015-05-29, http://www.cnki.net/kcms/detail/11.5602.TP.20150529.1611.003.html

ISSN 1673-9418 CODEN JKYTA8

Journal of Frontiers of Computer Science and Technology

1673-9418/2016/10(01)-0130-12



容量约束的自组织增量联想记忆模型*

孙桃，谢振平+，王士同，刘渊
江南大学数字媒体学院，江苏无锡214122

* The National Natural Science Foundation of China under Grant No. 61272210 (国家自然科学基金); the Natural Science Foundation of Jiangsu Province under Grant Nos. BK20130161, BK2011003 (江苏省自然科学基金).

Received 2015-03,Accepted 2015-05.

CNKI网络优先出版：2015-05-29, http://www.cnki.net/kcms/detail/11.5602.TP.20150529.1611.003.html

ISSN 1673-9418 CODEN JKYTA8

Journal of Frontiers of Computer Science and Technology

1673-9418/2016/10(01)-0130-12

E-mail: fcst@vip.163.com

http://www.ceaj.org

Tel: +86-10-89056056

摘要：自组织联想记忆神经网络因其并行、容错及自我学习等优点而得到广泛应用，但现有主流模型在增量学习较大规模样本时，网络节点数可能无限增长，从而给实际应用带来不可承受的内存及计算开销。针对该book=131,ebook=135问题，提出了一种容量约束的自组织增量联想记忆模型。以网络节点数为先决控制参数，结合设计新的节点间自竞争学习策略，新模型可满足大规模样本的增量式学习需求，并能以较低的计算容量取得较高的联想记忆性能。理论分析表明了新模型的正确性与有效性，实验分析同时显示了新模型可有效控制计算容量，提升增量样本学习效率，并获得较高的联想记忆性能，从而能更好地满足现实应用需求。

关键词：联想记忆；容量约束；增量学习；自组织；神经网络

1　引言

联想记忆[1]是人脑计算的一个核心功能，为使机器获得类人智能，研究者设计了各种可进行机器计算的联想记忆神经网络来对此进行模拟。联想记忆神经网络将对象模式显式或隐式地存储至网络节点，并通过示例样本的学习训练，实现对输入模式联想记忆出相应的输出模式。联想记忆主要分为自联想记忆和异联想记忆两种方式。前者输出受损或受污染输入模式的原始模式，后者输出输入模式的（因果）相关模式[2]。人工联想记忆神经网络因其具有较好的抗噪性、分布式信息存储能力、稳定性，并在一定程度上模拟了人类大脑对信息的记忆、识别和联想等功能，已大量应用于人脸识别[3]、模式识别[4]、图像和声音识别、机器人[5]等领域。

自20世纪80年代开始，联想记忆神经网络逐渐成为机器学习的重要研究领域之一。以经典的Hopfield网络[6]为标志，联想记忆模型经历了从全连接网络到稀疏连接网络，从单层单向到多层多向，从自联想到异联想[7]，从一对一联想到一对多甚至多对多联想，从二值型到非二值型，从简单网络到复杂网络[8]的发展。目前已提出的一些联想记忆模型有：基于动态突触的神经网络联想记忆模型[9]，其在存储容量上拥有比Hopfield联想记忆网络更优秀的性能；基于模糊学的神经网络联想记忆模型[10]，其利用模糊运算能够很好地抵抗噪声，具有较好的容错能力；基于自组织的神经网络联想记忆模型[11]，其调节神经元连接动力学形成网络拓扑结构，使迭代收敛速度较快。

虽然现有联想记忆神经网络性能较早期的模型已有较大提高，但许多受容量效率限制而实用性并不强。此外，大部分联想记忆神经网络的学习方法主要聚焦于常规的样本训练方式，对于增量地学习样本数据问题，则涉及较少，难以在大数据环境下演化地提升模型的计算性能。针对容量效率和增量学习[12]问题，现有一些方法如有界支持向量机[13]和在线球向量机[14]（online ball vector machine，OBVM）提出了一些解决方法，但此类方法主要针对二分类问题，不适用于复杂联想记忆输出要求。

针对上述问题，本文提出了一种容量约束的自组织增量联想记忆模型（self-organizing incremental associative memory model under capacity constraint，CCGAM）。新模型以控制网络节点数为手段，通过引入一种新的节点自竞争学习策略，实现模型在大规模增量可学习样本环境下的性能演化提升[15]，在获得较好模型性能的同时保持较低且可控的内存及计算要求。这为联想记忆神经网络相关应用及理论研究提供了一种非常有意义的新方法。

2　相关模型

作为早期Hopfield联想记忆神经网络模型的推广，Kosko等人[16]提出了一种双向联想记忆模型（bidirectional associative memory，BAM）。BAM是一种两层非线性反馈神经网络，可以用较小的相关矩阵实现有效的异联想。但BAM存在的补码问题和连续性假设限制了其存储容量和纠错能力，且其仅能处理二值型模式数据，实用性仍不强。

Wang等人[17]提出了一种新的模糊形态学联想记忆模型（fuzzy morphological associative memories，FMAM）。FMAM结合了形态学联想记忆[18]（morphological associative memories，MAM）和模糊联想记忆[19]（fuzzy associative memories，FAM），用模糊算子(∨，⋅)和(∧，⋅)代替FAM中的(∨，∧)算子，并具有较好的可解释性，其中提供了一种模糊规则集可完全联想回忆的新编码方法。FMAM的模糊算子能够有效地抑制样本噪声的干扰，在学习样本差异较大，受污染严重的情况下仍可拥有较好的联想记忆性能。虽然如此，但FMAM不具备增量学习能力，不适合学习条件复杂，学习样本规模大的情况，也不具有异联想功能。

为实现联想记忆神经网络的增量学习[20]，Furao等人提出了一种自组织增量神经网络[21]（self-organizing incremental neural network，SOINN）。SOINN采用无监督增量学习方法，实现对复杂分布数据的增量在线学习，并能够近似得到输入数据的分布，以自组织聚类方法估计出数据的类群数。进一步，Furao等人[22]在SOINN基础上提出了一种广义联想记忆模型（general associative memory，GAM）。GAM是一种三层网络结构的通用联想记忆神经网络模型，其采用有监督学习方法，具有较好的广义性和联想记忆性能，同时支持自联想和异联想记忆输出。GAM模型结构如图1所示，包括输入层、记忆层和联想层。输入层接受输入模式数据以及它们间的关系；记忆层与输入层为全连接，将输入模式数据经变换后存储至对应的记忆子网中；联想层中的每个神经节点与对应的记忆子网相关联，并与联想层其他节点间用有向边表示联想计算通路。

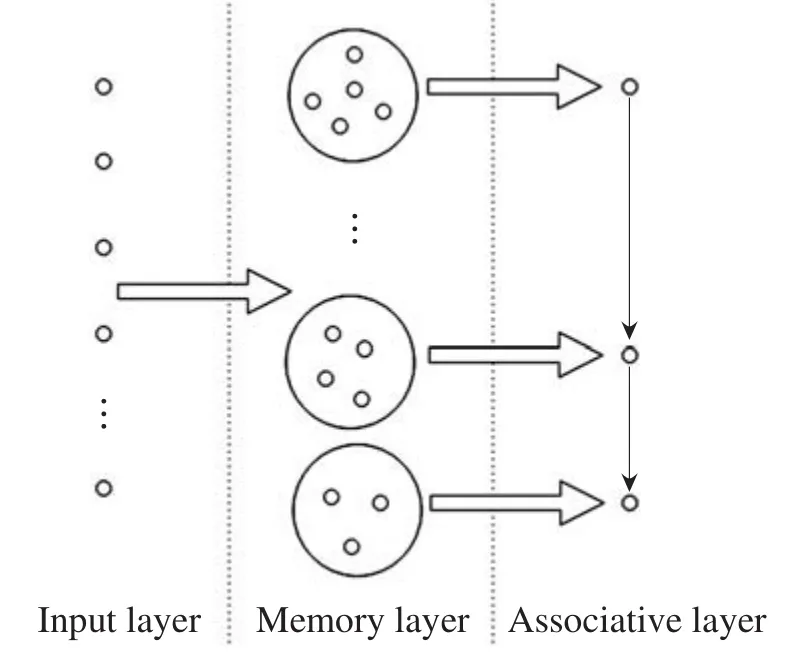
Fig.1 Three-layer network structure of GAM图1　GAM三层网络结构

GAM记忆层对样本进行学习时，首先在记忆层中找到对应该样本标签的子网络，然后在子网络中找到距离要学习样本最近的节点（冠军节点）和次近节点（亚军节点）；随后计算输入样本与冠军节点的距离s，并判断s与冠军节点相似性阈值Th之间的大小关系，若s大于Th，则将该学习样本作为新节点插入，否则更新冠军节点和亚军节点的权值向量，更新规则如下：

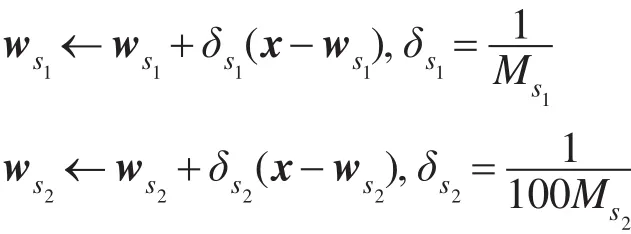
其中，w代表节点权值向量；s1为冠军节点；s2为亚军节点；x为训练样本；M为节点被选为冠军节点的次数。冠军节点的相似性阈值更新如下：

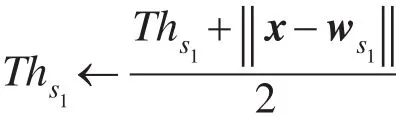
如果冠军节点和亚军节点之间没有连接边，添加一条边连接冠军和亚军节点，并将边年龄(age)设为0，然后将所有与冠军节点相连的边年龄加1。如果边的年龄大于预先定义的agemax，删除该边。最后，删除孤立节点。

GAM算法实现了多向自由联想记忆，可以处理实值型数据，能在不破坏全部神经元原有连接结构的情况下进行增量学习，并可对含噪输入模式联想回忆出真实模式。但GAM对初值过于敏感，且在大规模样本学习或者增量学习时，网络节点数量不可调节，存在无限增长的可能，相应的训练及联想回忆计算时间复杂度也会无限增大，这将导致其具有的增量学习能力难以发挥很好的实际作用，不能灵活地应对复杂的现实需求，广义适用性受到严重限制。

考虑到影响联想记忆神经网络模型计算和学习效率的控制参数为网络神经元节点数，以此为出发点，文中借鉴文献[13]的有界控制策略，结合新设计的节点间自竞争学习策略，提出了一种容量约束的自组织增量联想记忆模型CCGAM。

3　CCGAM

CCGAM网络模型结构仍采用GAM相同的形式（见图1），在学习方法上，首先考虑网络神经元数目具有上界约束，以限制网络的计算和存储规模，然后基于新提出的节点间自竞争学习策略，实现模型参数的学习。节点间自竞争学习策略不仅保证了学习结果的准确性，同时可有效避免GAM的初值敏感问题。下面分别从CCGAM的学习算法、联想算法、理论特性等几个方面展开描述。

3.1CCGAM学习算法

CCGAM学习算法包括记忆层学习算法和联想层学习算法。在记忆层学习算法中，为每个记忆子网络节点规模设置上界阈值Nmax。初始学习时，将同一标签的前Nmax个样本作为新节点添加至相应的记忆层子网络，这可有效避免GAM的初值敏感问题，强化对新知识的学习。在新引入的自竞争学习策略中，当子网络中节点数目达到上限阈值时，以一定概率淘汰对网络结构影响最小的节点，保证网络拓扑结构的稳定性。上述学习算法能够将每个子网络中节点数量控制在节点规模上界内，满足大规模增量样本的在线学习要求，并能有效地提高学习效率，避免不可控的内存及计算开销。CCGAM记忆层学习算法具体如算法1所示。

算法1 CCGAM记忆层学习算法

（1）初始化记忆层：A＝Φ，S＝Φ（A为记忆层节点集合，S为记忆层子网络集合）；

（2）设定每个模式子网络节点规模上界阈值Nmax；

（3）输入x∈RD到记忆层，x属于类cx（cx为x的标签）；

（4）若记忆层没有子网络cx，则添加cx，S＝S∪{cx}，A＝A∪{}，w＝x，＝1，转步骤（3）；

（6）计算子网络cx中节点数量Qcx；

（7）若Qcx＜Nmax，则将x作为新节点插入cx，＝x，＝1，转步骤（3）；

（9）若d1＞d2且r＜1/Ms3，删除s3，x作为新节点插入cx中，＝x，＝1，否则，更新ws1，ws1← ws1＋δs1(x−ws1)，其中δs1＝1/Ms1；

（10）如果训练没有结束，转步骤（3）。

分析算法1中步骤（6）和（7）可知，CCGAM将前Nmax个样本全部作为新节点添加到网络，若其中含有两个噪声点P1、P2（如图2所示），则其在后续样本学习过程时被选中冠军节点的概率将较小，最终将由步骤（8）和（9）的自竞争策略淘汰掉。而GAM对于样本初值过于敏感，在其学习前两个受污染样本后，添加P1、P2两个噪声点到网络中，两点的相似性阈值Th均被更新为P1与P2之间的欧氏距离d。由于后续样本点到P1或P2的距离小于Th，导致GAM始终更新P1、P2节点的权值，对新知识的学习能力较弱。

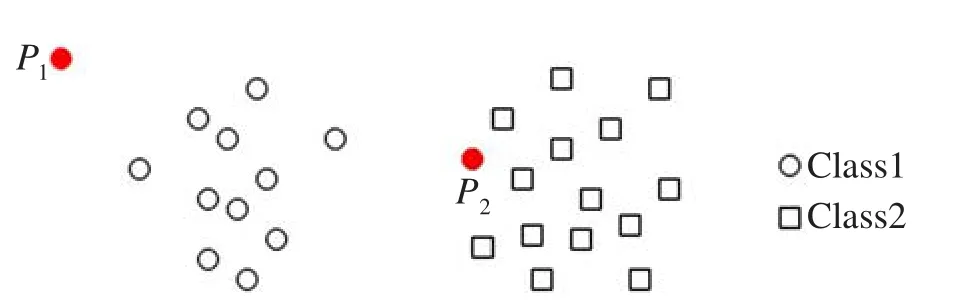
Fig.2 Initializing samples with noises图2　初始含噪声样本数据

CCGAM联想层学习算法仍采用与GAM相同的算法，以学习不同类别输入输出模式间的异联想关系，具体见算法2。其中，输入模式经算法1学习至记忆层后，在联想层建立与记忆层中每个子网络一一对应的节点，然后通过在联想层节点间建立有向箭头表示每个输入模式间的异联想关系，有向箭头权重表示联想优先级。

算法2 CCGAM联想层学习算法

（1）初始化联想层：B＝Φ，D＝Φ（B为联想层节点集合，D为联想层有向边集合）；

（2）输入x、y向量，x∈RD，x标签cx，y∈Rm，y标签cy；

（3）用算法1分别将x、y学习到记忆层；

（4）若联想层中没有代表cx的节点b，则插入新节点b代表cx，B＝B∪{b}，cb＝cx，mb＝0，wb＝x（mb为b引用次数，wb为b权值，cb为b名称）；

（5）否则，更新节点b的m值，mb←mb＋1，找到记忆层cx中M值最大的节点i，，更新b权值；

（6）若联想层中没有代表cy的节点d，则插入新节点d代表cy，B＝B∪{d}，cd＝cy，md＝0，wd＝y；

（7）否则，找到cy中M值最大的节点i，i＝，更新d权值；

（8）设置cd为b的序号mb的响应节点，RCb[mb]＝cd（RCb为b的响应节点）；

（9）若b、d无有向边相连，用有向边将b、d相连，b出发，d结束，添加有向边(b，d)到集合D，D＝D∪{(b，d)}，设置(b，d)权值w(b，d)＝1；

（10）否则，更新(b，d)权值w(b，d)←w(b，d)＋1。

3.2CCGAM联想算法

不完全相同于GAM模型，CCGAM联想算法采用的自联想算法和异联想算法分别如算法3和算法4所示。与GAM的自联想算法不同，算法3在记忆层中使用输入模式x对应模式子网络中节点间最大距离作为自联想输出有效的置信阈值，以取得更高的自联想准确性。

算法3 CCGAM自联想算法

（1）输入向量x；

（3）计算ck中任两节点间的距离最大值smax＝；

（4）若smin大于smax，则自联想失败，否则，输出自联想结果wk和标签ck。

算法4 CCGAM异联想算法

（1）输入线索向量x；

（2）用算法3找出x在记忆层中所属的子网络cx；

（3）在联想层找到代表cx的节点bx；

（4）按响应优先级输出bx所有响应节点。

CCGAM的异联想算法与GAM相同，能够联想出输入线索模式的所有响应模式，并根据响应优先级输出。首先由算法3联想出线索模式在记忆层中的子网络，然后找到该子网络在联想层中对应的节点，最后按照响应优先级依次输出所有的响应节点，实现多对多联想。如图3所示，x1是线索模式类在联想层中的代表节点，其响应节点为x2、x3、x4，算法4将根据响应节点对应的优先级w1、w2和w8的大小顺序依次输出响应节点。

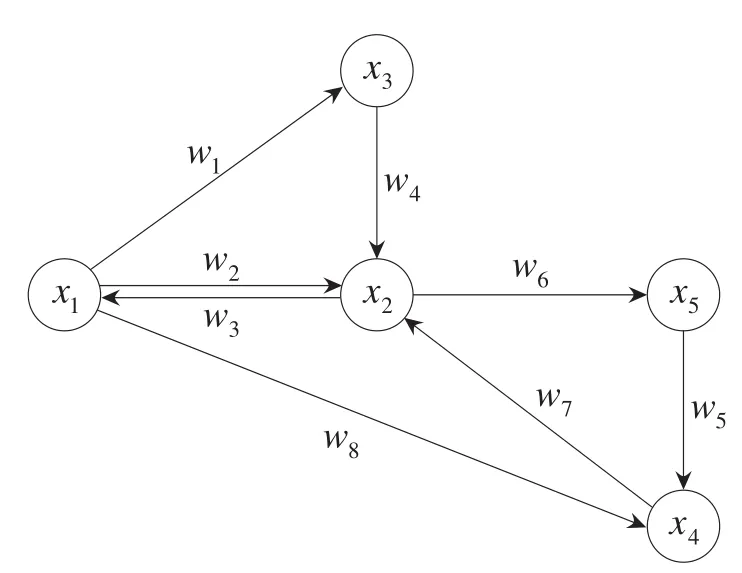
Fig.3 Structure of associative layer of CCGAM图3　CCGAM联想层结构模型

3.3CCGAM理论分析

3.3.1学习稳定性

CCGAM基于对样本的增量迭代学习而得到模型参数，为保证学习的可靠性，通常要求学习算法是渐近稳定的。对于CCGAM，在网络节点数达到上界时，通过自竞争策略更新或者替换某个节点，经分析可知有以下定理成立。

定理1 CCGAM对任一记忆层节点权值的迭代更新过程是收敛稳定的。

证明设有n个输入模式v1，v2，…，vn属于同一标签cv，CCGAM记忆层与cv对应的子网络中的节点数为m个，对cv中每个模式vi(i＝1，2，…，n)进行学习，定义冠军节点为，设某节点x被 p个模式选中为冠军节点，其中p＝(′，，…，)，假设p足够大，随着学习次数增加，则第n次学习模式(∈p)，对节点x的权值wx更新的递归公式为：

节点x被迭代更新n次的最终权值为所有学习模式的平均值，即CCGAM对任意n个输入模式的迭代学习过程是收敛稳定的。学习算法针对模型一致的学习样本时，学习结果是统计一致的。□

3.3.2计算复杂度

假设CCGAM神经元规模上界阈值为Nmax，待训练的模式为x，x的标签为cx，s1、s2分别为cx中与x的欧式距离最近的神经元节点和次近的神经元节点，定义：

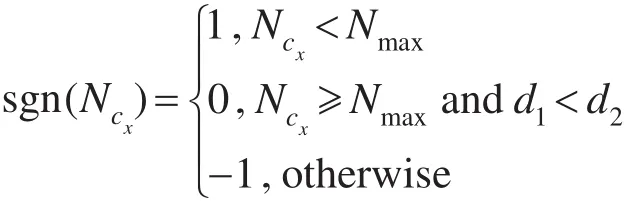
其中，d1＝‖ws1−x‖，d2＝‖ws2−ws1‖；Ncx是网络中对应标签cx的神经元节点数。如果sgn(Ncx)值为1，x直接作为新的神经元添加；如果sgn(Ncx)值为0，对s1的权值进行更新，ws1＝ws1＋∆ws1，其中∆ws1＝(x−ws1)/Ms1；如果sgn(Ncx)值为−1，找到标签为cx的子网络中M值最小的神经元节点并以1 M的概率删除，再将x作为新的神经元添加到cx。由此可知，在CCGAM记忆层，每个子网络中神经元数最多为预先设定的Nmax。

设一个集群的训练模式总数为M（M无限大），当网络中每增加一个神经元，训练一个样本模式所需增加的时间开销为τ。对于CCGAM，训练前Nmax个模式时，网络神经元数是线性增加的，空间复杂度为O(n)，所需训练时间开销关于训练样本数呈二次函数增长；训练超过Nmax个模式时，由于网络中神经元规模已达到上界且不再增加，空间复杂度为O(1)，训练时间关于训练样本数呈线性增加。对于GAM，每个训练样本是否作为新的神经元添加到网络中且有一定的随机性。假设GAM将每个训练模式作为新神经元添加的概率为ρ(ρ＜1)，空间复杂度为O(n)，训练时间关于训练样本数始终呈二次函数增长。CCGAM( T1)和GAM( T2)的训练时间随着训练样本模式数n的变化函数整理如下：

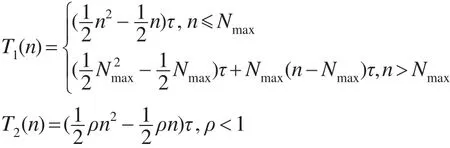
GAM、CCGAM训练时间关于训练模式规模的变化趋势如图4所示（其中a＝Nmax，γ＝ρ）。从图中可知，对于单个学习样本，其序号数等于a时，CCGAM的学习时间复杂度为O(n2)，当序号数大于a时，学习时间复杂度为O(n)；而GAM的学习时间复杂度始终为O(n2)。当学习样本较大时，新学习一个样本所需的计算时间，GAM要远大于CCGAM。

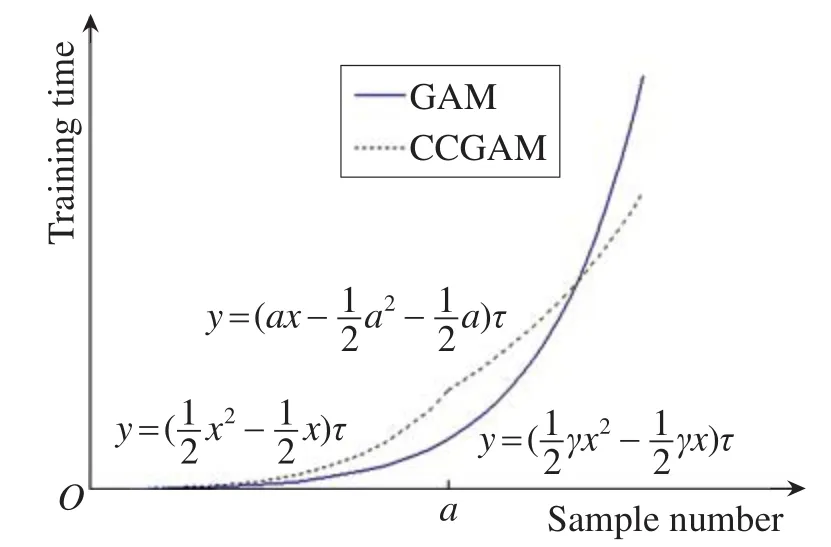
Fig.4 Training time on different sample number for GAM and CCGAM图4　GAM与CCGAM训练时间关于训练模式数的变化关系

4　实验研究

本文分别基于字母识别、性别判别和烟雾检测问题对CCGAM的实际性能进行分析。实验计算配置如下：内存4.00 GB，CPU为Intel@CoreTMi5-3470，主频3.20 GHz，操作系统为64位，程序开发环境为C++平台、OpenCV和Boost程序库。

Fig.5 Binary letters images图5　二进制字母图像

4.1字母识别

本实验主要测试分析CCGAM模型的计算有效性、学习效率和联想记忆性能。字母识别对象如图5所示，有26个大写字母和26个小写字母，每个字母是一个7×7像素构成的二值图像，图像是由黑点（-1）和白点（1）构成，每个字母属于一个类，共52个模式类。

本部分实验中，首先对比分析GAM和CCGAM的学习效率和计算有效性。从每个原始字母图像49个像素点中随机选取10个点添加噪声，将其原像素值更改为其相反值，如图6所示，并分别重复100，150，…，1 000次，共生成19组含噪训练样本作为训练集数据。针对上述19组训练集Di(i＝1，2，…，19)，分别使用GAM和CCGAM进行19次训练，训练完后对两者进行一次增量学习，其中Nmax取值为10。图7分别给出了CCGAM和GAM模型的子网节点数、训练时间及增量学习时间随学习次数的变化关系图。

Fig.6 Noise patterns generated from an original pattern图6　对原始模式随机加噪生成噪声模式

图7（a）是CCGAM和GAM在训练样本逐渐增加的情况下，每个类在记忆层中产生的节点数。由于GAM每个类训练后记忆层产生的节点数并不一样，实验中统计的节点数是52个类的平均节点数。从图中可以得出，CCGAM每个子网络中节点数始终控制在10，而GAM随着训练样本的增加，节点数也逐渐增加，图像中显示GAM的节点数与训练样本大致呈线性增加关系。

图7（b）是在训练样本增加的情况下，CCGAM 和GAM对每个类的训练时间变化趋势曲线。由于CCGAM控制了网络节点数增长，随着训练样本的增加，CCGAM的训练时间关于训练样本数呈线性增长，训练时间复杂度为O(n)。而GAM的网络节点数随着训练样本增加而不断增加，其训练时间关于训练样本数呈二次函数增加，复杂度为O(n2)。同时也证明了3.3节中关于两者时间复杂度的理论分析。

进一步，仍基于字母识别问题测试分析CCGAM的异联想能力。实验中将大写字母图像作为线索模式，对应的小写字母图像作为响应模式，如A→a，B→b，…，Z→z，以这样的模式对形式输入网络进行训练，并通过调整Nmax值比较不同节点数限定下的CCGAM异联想学习性能。采取前述相似加噪方法对每个原始模式加噪生成每个类包含500个不同噪声模式的数据集作为训练集D，同样方法生成另一组只含线索模式的数据集作为测试集T。实验中，固定训练集D，Nmax分别取值10，15，20，…，60，用算法2对CCGAM进行11组训练，每次训练完用算法4对测试集T进行测试，统计异联想性能。由于GAM不能控制调节网络中节点数，本实验仅用训练集D和测试集T对GAM进行一次实验，用式（1）计算GAM的平均节点数，实验结果如表1所示。

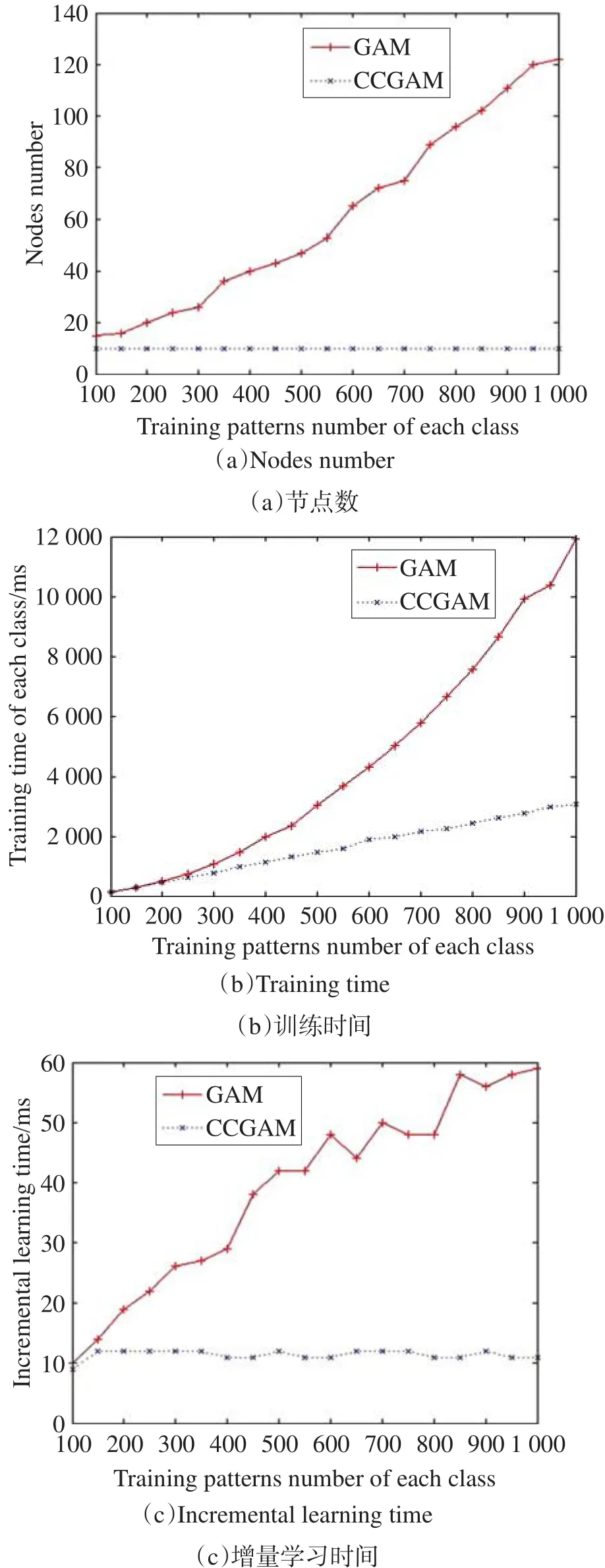
Fig.7 Performance comparison of GAM and CCGAM图7　GAM与CCGAM的性能对比

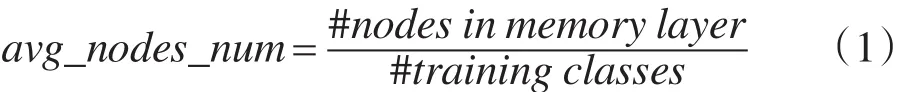
表1中的实验结果表明，对于CCGAM，在网络节点数限定较小时，增加网络节点数，可以提高联想准确率，但当节点数达到某一上界后，准确率趋于稳定。这一实验结果表明，为取得实用有效的性能，记忆子网节点数仅需控制在某个问题相关的上界范围内，并不需要无限增大。对比表1中GAM与CCGAM性能可以发现，两者在相近的子网节点数时，所取得的性能相当，这也表明CCGAM的学习算法是有效且可靠的。

4.2性别判别

为了测试分析CCGAM在复杂实值型数据集中的性能，本实验选用美国CTTP发起的人脸识别技术工程（FERET）所采集的通用人脸库作为数据集，包括414张不同男性脸部图像和309张不同女性脸部图像。所有图像均为80×80像素的标准TIF格式灰度图，图像人物包含不同的表情、姿态、种族和年龄，如图8、图9所示。

Table 1 Recalling performance obtained by GAM and CCGAM表1　GAM与CCGAM联想记忆测试结果对比

Fig.8 Some female facial images图8　部分女性脸部图像

Fig.9 Some male facial images图9　部分男性脸部图像

首先，从数据集中随机选取200张男性图像和200张女性图像作为训练集，剩余323张图像作为测试集，用算法1训练，算法3进行测试，计算Nmax在不同取值下CCGAM的自联想准确率；然后再重新随机抽取训练集和测试集，对应每个Nmax值共进行n＝20次，用式（2）计算每个Nmax值对应n次随机抽取样本的自联想准确率ratei(i＝1，2，…，n)；最后用式（3）统计每个Nmax值对应的CCGAM平均联想准确率avg_rate。CCGAM在Nmax值分别取5，10，15，…，100时的平均联想准确率如图10所示。

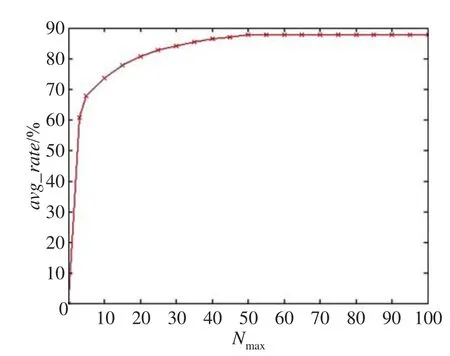
Fig.10 Accuracy changes with different nodes number on CCGAM图10　CCGAM准确率随节点数的变化曲线

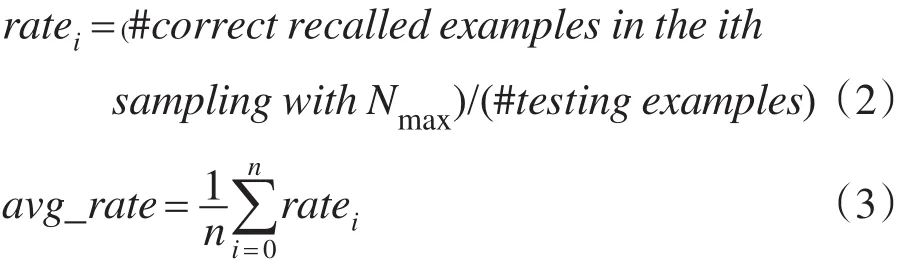
由图10可以看出，Nmax值在0～20范围内时，CCGAM自联想准确率随着Nmax值增加而提高较快；在20～50范围内时，CCGAM自联想准确率提高逐渐减缓；而当Nmax值超过50时，CCGAM自联想准确率趋于稳定。

为了进一步比较CCGAM的性能，表2给出了3种分类算法包括SVM[17]、OBVM[13]和GAM算法的实验结果。实验中，CCGAM节点数固定为50，在保持实验条件不变的情况下，统计另外3种算法的各项性能指标，包括节点数/支撑向量数（Ns/SVs）、训练时间（T）、一次增量学习时间（I）和准确率（Accuracy），其中Accuracy是由式（3）计算20次实验结果的均值。另外统计了准确率方差，用来衡量准确率的稳定性。具体实验结果如表2所示，加粗部分为每类结果的最优值。

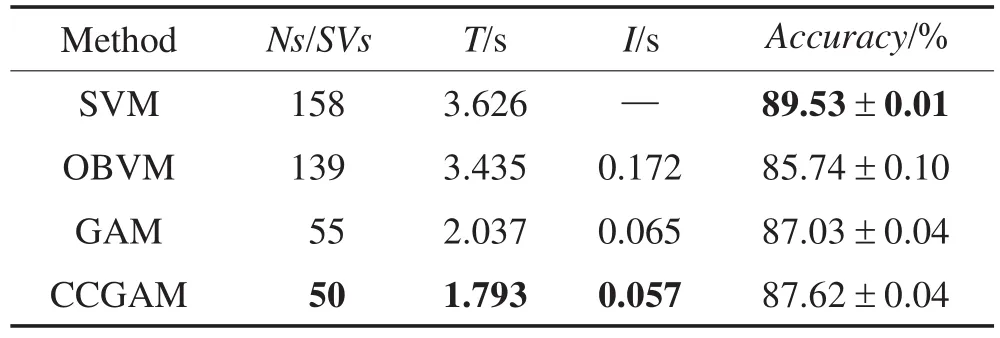
Table 2 Performance of CCGAM and other methods in gender recognition表2　CCGAM和其他方法在性别识别实验中性能比较

由表2可以看出，和其他方法相比，CCGAM的网络节点数、训练时间和增量学习时间均具有优势，其联想准确率稍低于SVM，但高于另外两种方法。

4.3烟雾检测

进一步选取烟雾检测问题[23-24]作为实验对象，评估CCGAM在实际问题上的应用性能。烟雾特征具有很强的非线性特征，为更好地辨识烟雾与非烟雾，分类器通常需要对大量的不同场景特征数据进行学习。文献[23-24]针对视频烟雾检测问题进行研究，提出了新的快速烟雾特征提取方法。此处同样采用文献[24]的视频烟雾图像特征提取方法。其中对任一分析区域块，提取4个基本的烟雾飘动性特征量，再计算WT时间窗内的均值和方差作为附加特征量，形成12维的烟雾特征。实验数据集包含真实烟雾（正例）和非烟雾（反例）的特征数据共357 006个（正例221 191个，反例135 815个）。首先设置不同CCGAM节点规模上界阈值Nmax，分析其对识别性能的影响。实验中，分别取Nmax＝200，400，…，2 000，共10组，每次对数据集随机抽取80%共285 605个特征数据作为训练集Di，20%作为测试集Ti，用式（2）计算联想准确率（Accuracy），并统计对应的训练时间（T）和增量学习时间（I），实验结果如表3所示。从表3中可知，随着Nmax增加，CCGAM的训练时间T和增量学习时间I均会增加，而联想准确率当Nmax在200～ 1 600范围内时会提高，超过1 600后基本保持稳定。

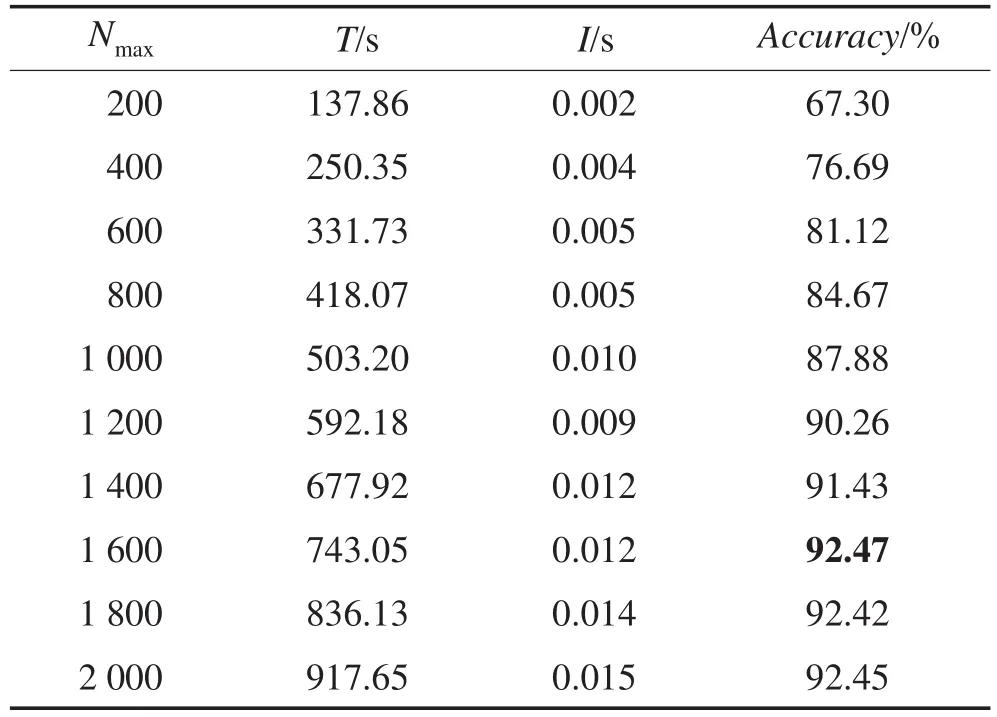
Table 3 Smoke detection performance with different Nmax表3　Nmax对烟雾检测的性能影响

进一步，将CCGAM节点数设为1 600，与SVM、OBVM和GAM的烟雾检测性能进行对比。其中对4种算法的网络节点数/支撑向量数（Ns/SVs）、训练时间（T）、增量学习时间（I）和联想准确率（Accuracy）进行了统计，T和I反映了算法的计算效率，实验结果见表4，对最优结果作加粗显示。分析可知，和其他3种方法相比，CCGAM仅需最少的节点数和最小的训练时间、增量学习时间，获得了与其他3种方法相当的联想性能。

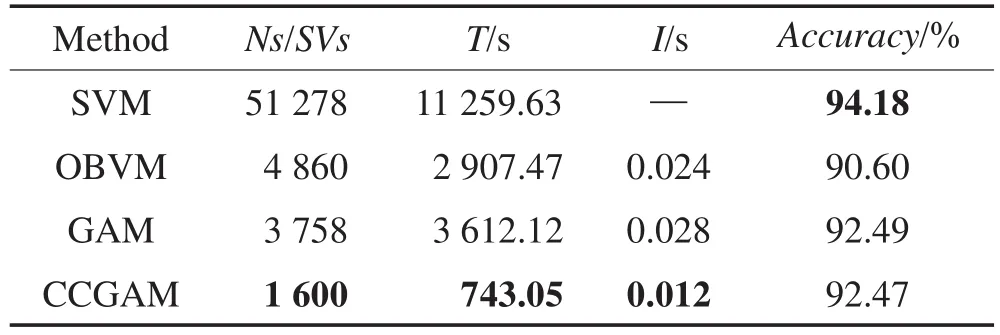
Table 4 Smoke detection performance of CCGAM and other methods表4　CCGAM和其他方法的烟雾检测性能对比

综合表3、表4可知，CCGAM能够较好地适用于大规模增量样本学习，且可以根据应用问题自身特点调整Nmax，使得模型在保持较高性能的前提下仅需较低的计算资源。综合地，相比现有的支持增量学习的通用计算模型，CCGAM具有较明显的计算效率优势，并保持较高的模型性能。

5　结论与展望

为适应大数据学习要求，联想记忆算法不仅要求有较高的联想准确率，而且要求有较高的计算效率。本文提出了一种容量约束的自组织增量联想记忆模型（CCGAM），针对大规模可学习样本，新模型能够在网络神经元数量可控的方式下实现增量学习，极大地提高了样本模式的学习效率。CCGAM可避免GAM存储容量过大和初值敏感问题，并能取得较高的联想性能。实验结果表明，将节点数控制在较小范围后，新模型仍能得到较好的联想准确率，而其在计算效率和内存开销上明显优于GAM和其他传统算法，这为联想记忆在大数据学习背景下的应用提供了一种新的解决方法。

虽然如此，文中所研究的联想记忆模型没有涉及模式特征学习问题，而是直接基于原始模式数据或已提取的特征数据作为输入模式，这在一定程度上限制了新模型的广泛适用性，这也将是下一阶段的重要研究方向。

References:

[1] Michel A N, Farrell J A. Associative memories via artificial neural networks[J]. IEEE Control Systems Magazine, 1990, 10(3): 6-17.

[2] Haykin S. Neural networks[M]. Beijing: Tsinghua University Press, 2001.

[3] Wu Xiaojun, Zhang Yuanyuan, Wang Shitong, et al. Improved fuzzy neural network and its application to face recognition[J]. Micronano Electronic Technology, 2007, 44(7): 465-469.

[4] Ozturk M C, Principe J C.An associative memory readout for ESNs with applications to dynamical pattern recognition[J]. Neural Networks, 2007, 20(3): 377-390.

[5] Itoh K, Miwa H, Takanobu H, et al. Application of neural network to humanoid robots—development of co-associative memory model[J]. Neural Networks, 2005, 18(5): 666-673.

[6] Hopfield J J. Neural networks and physical systems with emergent collective computational abilities[J]. Proceedings of the National Academy of Sciences, 1982, 79(8): 2554-2558.

[7] Azuela J H S. A bidirectional hetero-associative memory for true-color patterns[J]. Neural Processing Letters, 2008, 28(3): 131-153.

[8] Zhou Zhihua, Chen Shifu. Neural network ensemble[J]. Chinese Journal of Computers, 2002, 25(1): 1-8.

[9] Namarvar H H, Liaw J S, Berger TW.Anew dynamic synapse neural network for speech recognition[C]//Proceedings of the 2001 International Joint Conference on Neural Networks, Washington, USA, Jul 15-19, 2001. Piscataway, USA: IEEE, 2001, 4: 2985-2990.

[10] Chung F, Lee T. On fuzzy associative memory with multiplerule storage capacity[J]. IEEE Transactions on Fuzzy Systems, 1996, 4(3): 375-384.

[11] Carpenter G A, Grossberg S. A massively parallel architecture for a self-organizing neural pattern recognition machine[J]. Computer Vision, Graphics, and Image Processing, 1987, 37(1): 54-115.

[12] Yu Cui, Zhang Rui, Huang Yaochun, et al. High-dimensional kNN joins with incremental updates[J]. Geoinformatica, 2010, 14(1): 55-82.

[13] Zhao Peilin, Wang Jialei, Wu Pengcheng, et al. Fast bounded online gradient descent algorithms for scalable kernel-based online learning[J]. arXiv: 1206.4633, 2012.

[14] Yang Haifeng, Liu Yuan, Xie Zhenping, et al. Efficiently training ball vector machine in online way[J]. Journal of Computer Research and Development, 2013, 50(9): 1836-1842.

[15] Mininno E, Neri F, Cupertino F, et al. Compact differential evolution[J]. IEEE Transactions on Evolutionary Computation, 2011, 15(1): 32-54.

[16] Kosko B. Bidirectional associative memories[J]. IEEE Transactions on Systems, Man and Cybernetics, 1988, 18(1): 49-60. [17] Wang Min, Wang Shitong, Wu Xiaojun. Initial results on fuzzy morphological associative memories[J]. Chinese Journal of Electronics, 2003, 31(5): 690-693.

[18] Ritter G X, Sussner P, Diza-de-Leon J L. Morphological associative memories[J]. IEEE Transactions on Neural Networks, 1998, 9(2): 281-293.

[19] Wilamowski B M. Neural networks and fuzzy systems[J]. Mechatronics Handbook, 2002, 33(1): 32-26.

[20] Forster K, Monteleone S, Calatroni A, et al. Incremental kNN classifier exploiting correct-error teacher for activity recognition[C]//Proceedings of the 9th International Conference on Machine Learning and Applications, Washington, USA, Dec 12-14, 2010. Piscataway, USA: IEEE, 2010: 445-450.

[21] Furao S, Hasegawa O. An incremental network for on-line unsupervised classification and topology learning[J]. Neural Networks, 2006, 19(1): 90-106.

[22] Shen Furao, Ouyang Qiubao, Kasai W, et al. A general associative memory based on self-organizing incremental neural network[J]. Neurocomputing, 2013, 104: 57-71.

[23] Wang Tao, Liu Yuan, Xie Zhenping. Flutter analysis based video smoke detection[J]. Journal of Electronics and Information Technology, 2011, 33(5): 1024-1029.

[24] Xie Zhenping, Wang Tao, Liu Yuan, et al. A fast video smoke detection algorithm by analyzing fluttering[J]. Microelectronics and Computer, 2011, 28(10): 209-214.

附中文参考文献：

[3]吴小俊,张媛媛,王士同,等.改进的模糊神经网络及其在人脸识别中的应用[J].微纳电子技术, 2007, 44(7): 465-469.

[8]周志华,陈世福.神经网络集成[J].计算机学报, 2002, 25(1): 1-8.

[14]杨海峰,刘渊,谢振平,等.球向量机的快速在线学习[J].计算机研究与发展, 2013, 50(9): 1836-1842.

[17]王敏,王士同,吴小俊.新模糊形态学联想记忆网络的初步研究[J].电子学报, 2003, 31(5): 690-693.

[23]王涛,刘渊,谢振平.一种基于飘动性分析的视频烟雾检测新方法[J].电子与信息学报, 2011, 33(5): 1024-1029.

[24]谢振平,王涛,刘渊,等.一种飘动性分析的视频烟雾快速检测新算法[J].微电子学与计算机, 2011, 28(10): 209-214.

SUN Tao was born in 1991. He is an M.S. candidate at School of Digital Media, Jiangnan University. His research interests include machine learning and computer vision.

孙桃（1991—），男，安徽全椒人，江南大学数字媒体学院硕士研究生，主要研究领域为机器学习，计算机视觉。

XIE Zhenping was born in 1979. He received the Ph.D. degree in light industry information technology and engineering from Jiangnan University in 2008. Now he is an associate professor at Jiangnan University. His research interests include machine learning and cognitive computing.

谢振平（1979—），男，江苏常州人，2008年于江南大学轻工业信息技术与工程专业获得博士学位，现为江南大学副教授，主要研究领域为机器学习，认知计算。

WANG Shitong was born in 1964. He is a professor at School of Digital Media, Jiangnan University. His research interests include artificial intelligence, pattern recognition and bioinformatics.

王士同（1964—），男，江南大学数字媒体学院教授，主要研究领域为人工智能，模式识别，生物信息。

LIU Yuan was born in 1967. He is a professor at School of Digital Media, Jiangnan University. His research interests include network security and digital media.

刘渊（1967—），男，江南大学数字媒体学院教授，主要研究领域为网络安全，数字媒体。

Self-Organizing Incremental Associative Memory Model under Capacity Constraint*

SUN Tao, XIE Zhenping+, WANG Shitong, LIU Yuan
School of Digital Media, Jiangnan University, Wuxi, Jiangsu 214122, China
+ Corresponding author: E-mail: xiezhenping@hotmail.com

SUN Tao, XIE Zhenping, WANG Shitong, et al. Self-organizing incremental associative memory model under capacity constraint. Journal of Frontiers of Computer Science and Technology, 2016, 10(1)：130-141.

Abstract:Due to the advantages of self-organizing neural network like parallelism, fault freedom and self-learning, it has been widely used all over the place. However, in traditional associative memory neural networks, the number of network nodes will unlimitedly grow when they incrementally learning more and more samples, which inevitably leads to an unaffordable overhead of computation and storage. To solve this problem, this paper proposes a self-organizing incremental associative memory model under capacity constraint. By limiting the number of network nodes and introducing a self-competition strategy between network nodes, new model is capable of incrementally learning large-scale samples and can gain equivalent associative memory performance only requiring lower computing demand. The reasonability of model is proved by theoretical analysis. Moreover, the experimental results demonstrate that new model can effectively control computing consumption, improve the efficiency of incrementally learning new samples, and obtain comparative associative memory performance, which may preferably satisfy the demands of many practical applications.

Key words:associative memory; capacity constraint; incremental learning; self-organizing; neural network

文献标志码：A

中图分类号：TP18

doi:10.3778/j.issn.1673-9418.1505007