“超级全能生”2016高考全国卷26省联考(乙卷)(本试卷适用于使用全国卷Ⅰ地区)
“超级全能生”2016高考全国卷26省联考(乙卷)(本试卷适用于使用全国卷Ⅰ地区)
(时间:120分钟 满分:150分)
[编者按]本次考试由新东方优能中学、《教学考试》杂志社共同发起组织,全国26个省市的数十万考生参加,试题创新度较高,吻合高考命题趋势,本刊特刊发以供广大读者考前模拟检测,希望对大家备考有所帮助。
一、选择题(本题共12小题,每小题5分,共60分)

A.第一象限B.第二象限
C.第三象限D.第四象限
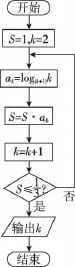
3.执行如图所示的程序框图,则输出的k为( )
A.7B.8
C.9D.10
4.(理)从1,2,3,4,5,6,7,8,9中任取七个不同的数,则这七个数的平均数是5的概率为( )

(文)根据如下样本数据:

?
得到的回归方程为y=bx+a,则( )
A.a>0,b>0B.a>0,b<0
C.a<0,b>0D.a<0,b<0
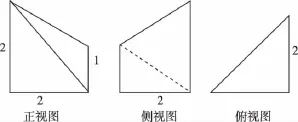
5.如图所示,某几何体的三视图,则该几何体的体积为( )


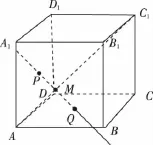
(文)如图,M是正方体ABCD-A1B1C1D1对角线AC1上的动点,过点M作垂直于面ACC1A1的直线与正方体表面分别相交于P,Q两点,设AM=x,PQ=y,则函数y=f(x)的图象大致为( )
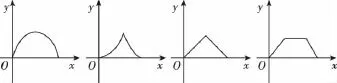
A B C D

11.(理)如图,在棱长为1的正方体ABCD-A1B1C1D1中,P为棱A1B1中点,点Q在侧面DCC1D1内运动,若∠PBQ=∠PBD1,则动点Q的轨迹所在曲线为( )
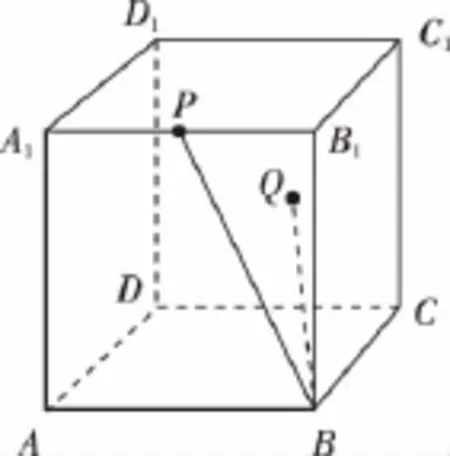
A.圆B.椭圆
C.双曲线D.抛物线
(文)点A是⊙O上的动点,点B是⊙O内的定点(不与点O重合),PQ垂直平分AB于Q,交OA于点P,则点P的轨迹是( )
A.直线B.圆
C.椭圆D.双曲线

二、填空题(本题共4小题,每小题5分,共20分)

(文)某校从五月开始,要求高三学生下午2:30前到校,甲班班主任李老师下午每天到校,假设李老师和小红同学在下午2:00到2:30之间到校,且每人在该段时间到校都是等可能的,则小红同学比李老师至少早5分钟到校的概率为____________.

(文)直线l⊥平面α,垂足是点P,正四面体OABC的棱长为2,点O在平面α上运动,点A在直线l上运动,则点P到直线BC 的距离的最大值为_____________.
三、解答题(本题共6小题,共70分)

18.(12分)(理)某商场五一进行抽奖促销活动,当日在该商场消费的顾客即可参加抽奖活动,抽奖情况如下:

消费金额X(元)[500,1 000)[1 000,1 500)[1 500,+∞)1 2 4______抽奖次数
抽奖箱中有9个大小形状完全相同的小球,其中4个红球、3个白球、2个黑球(每次只能抽取一个,且不放回抽取).第一种抽奖方式:若抽得红球,获奖金10元;若抽得白球,获奖金20元;若抽得黑球,获奖金40元.第二种抽奖方式:抽到白球或黑球才中奖,若抽到白球,获奖金50元;若抽到黑球,获奖金100元.
(Ⅰ)若某顾客在该商场当日消费金额为2 000元,用第一种抽奖方式进行抽奖,求获得奖金70元的概率.
(Ⅱ)若某顾客在该商场当日消费金额为1 200元,请同学们告诉这位顾客哪种抽奖方式对他更有利.
(12分)(文)某校高三文科600名学生参加了12月的模拟考试,学校为了了解高三文科学生的数学、外语情况,利用随机数表法从中抽取100名学生的成绩进行统计分析,将学生编号为:000,001,002,003,…,599.
(Ⅰ)若从第6行第7列的数开始右读,请你依次写出最先抽出的5个人的编号(下面是摘自随机用表的第4行至第7行);
12 56 85 99 26 96 96 68 27 31 05 03 72 93 15 57 12 10 14 21 88 26 49 81 76
55 59 56 35 64 38 54 82 46 22 31 62 43 09 90 06 18 44 32 53 23 83 01 30 30
16 22 77 94 39 49 54 43 54 82 17 37 93 23 78 87 35 20 96 43 84 26 34 91 64
84 42 17 53 31 57 24 55 06 88 77 04 74 47 67 21 76 33 50 25 83 92 12 06 76
(Ⅱ)抽出的100名学生的数学、外语成绩如下表:
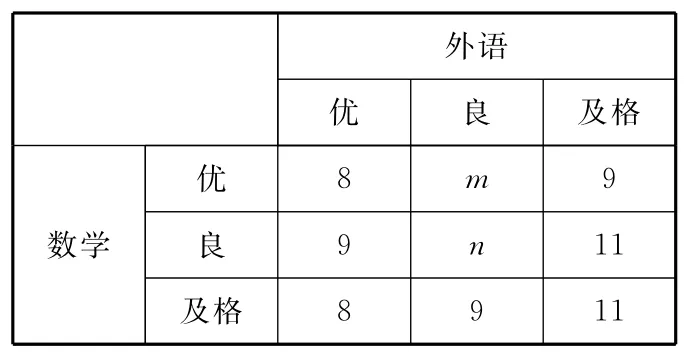
外语优良及格8 9 11__优8 m___ ___9___数学___良9 n 11__及格
若数学的优秀率为35%,求m,n的值;
(Ⅲ)在外语成绩为良的学生中,已知m≥12,n≥10,求数学成绩优比良的人数少的概率.
19.(12分)(理)已知三棱锥P-ABC,平面PBC⊥平面
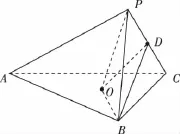
(Ⅰ)在边PA上是否存在一点E,使得AC⊥平面BOE.若存在,确定点E的位置;若不存在,请说明理由;
(Ⅱ)求二面角P—BD—O的余弦值.
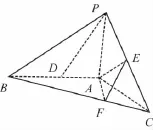
(12分)(文)如图,已知三棱锥P—ABC,PA⊥平面ABC,AB=AC=AP,∠BAC=90°,D,E分别为AB,PC的中点,BF=2FC.
(Ⅰ)求证:PD∥平面AEF;
(Ⅱ)求AC与平面AEF所成角的正弦值.
(Ⅰ)求抛物线C的方程;
(Ⅱ)过点F的直线l交抛物线C于A,B两点,AB的垂直平分线m与C相交于C,D两点,使=0,求直线l的方程.
第二,真菌、衣原体、支原体、滴虫等所致的阴道感染,慎重选药。一般情况下,真菌感染选用咪康唑栓,病情较重且炎症反复复发,联合应用氟康唑。衣原体与支原体感染,需进行药敏试验,根据试验结果,选择抗菌药。滴虫性阴道炎,应口服甲硝唑或替硝唑,同时性伴侣也应该进行治疗。
(Ⅰ)求椭圆C的方程;
(Ⅱ)过F2的直线交椭圆C于A,B两点,圆M为△ABF1的内切圆,求圆M的面积的最大值.
(Ⅰ)当x≥1时,若f(x)≥a x(-1)恒成立,求a的取值范围;
请考生在第22~24三题中任选一题作答,如果多做,则按所做的第一题计分.
22.(10分)已知AB,DE为圆O的直径,CD⊥AB于N,N为OB的中点,EB与CD相交于点M,切线EF与DC的延长线交于点F.
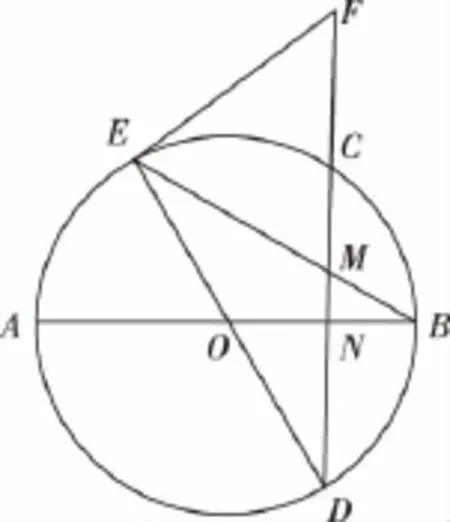
(Ⅰ)求证:EF=FM;
(Ⅱ)若圆O的半径为1,求EF的长.
(Ⅰ)求曲线C与直线l的直角坐标方程;
参考答案
1.(理)C (文)C
2.(理)B (文)D
3.B
4.(理)C (文)B
5.D
6.(理)D (文)A
7.(理)A (文)A
8.A
9.(理)C (文)C
10.(理)C (文)D
11.(理)C (文)C
12.(理)D (文)B
13.[3,+∞)
17.(理)解:(Ⅰ)由2Sn+an=n2+2n+2,①
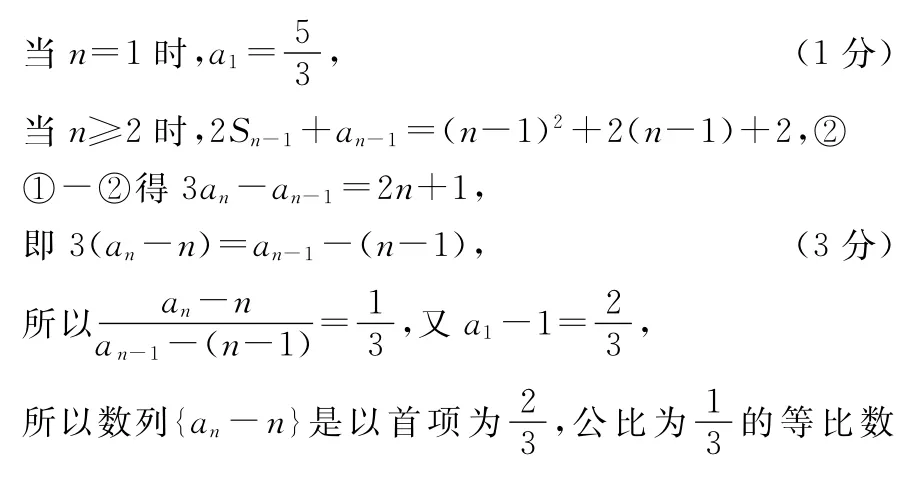

18.(理)解:(Ⅰ)因为X=2 000,所以该顾客有4次抽奖机会,得奖金70元,则有两种情形:抽得3红1黑;抽得1红3白.
(Ⅱ)因为X=1 200,所以该顾客有两次抽奖机会.
用第一种抽奖方式抽奖,获奖金额ξ(元)可能为20、30、40、50、60、80,则

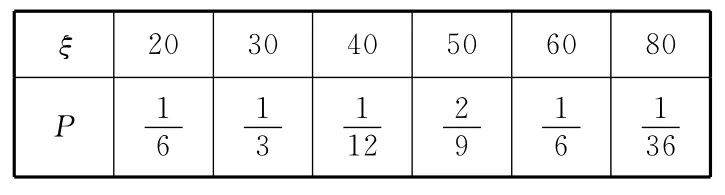
?
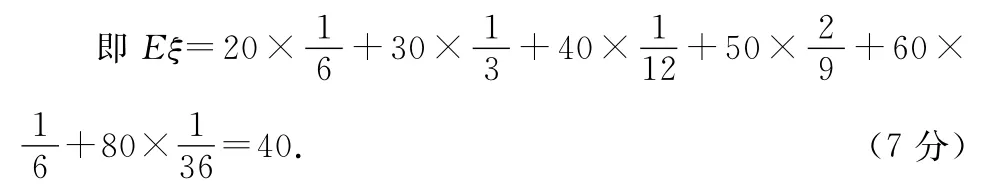
用第二种抽奖方式抽奖,获奖金额η(元)可能为0、50、100、150、200,则

所以该顾客选择第二种抽奖方式会更好.(12分)
(文)解:(Ⅰ)编号依次为:544,354,378,520,384.(2分)
因为8+9+8+18+n+9+9+11+11=100,得n=17.(5分)
(Ⅲ)由题意m+n=35,且m≥12,n≥10,
所以满足条件的(m,n)有
(12,23)、(13,22)、(14,21)、(15,20)、(16,19)、(17,18)、(18,17)、(19,16)、(20,15)、(21,14)、(22,13)、(23,12)、(24,11)、(25,10)共14种,且每组出现都是等可能的.
(8分)
记:“数学成绩优比良的人数少”为事件M,则
事件M包含的基本事件有(12,23)、(13,22)、(14,21)、(15,20)、(16,19)、(17,18)共6种,所以(12分)
19.(理)证明:(Ⅰ)存在点E为AP的三等分点且AE=2EP.(1分)
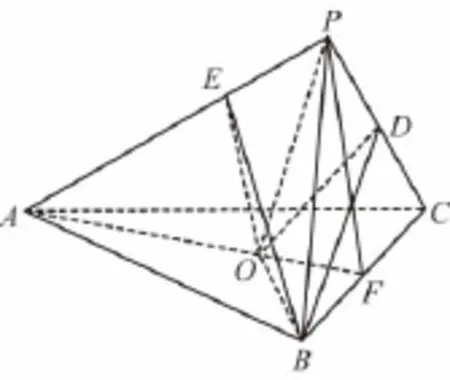
因为△ABC为等边三角形,O为中心,所以BO⊥AC,(2分)
连接AO延长交BC于F,连接PF,F为BC的中点,AO=2OF,又PB=PC,所以PF⊥BC,
又平面PBC⊥平面ABC,所以PF⊥平面ABC,即PF⊥AC,
所以EO∥PF,EO⊥AC,
又EO∩BO=0,所以AC⊥平面BOE,
所以存在点E为AP的三等分点且AE=2EP.(6分)
(Ⅱ)取BC的中点F,连接PF,
因为PB=PC,所以PF⊥BC,
又平面PBC⊥平面ABC,
所以PF⊥平面ABC,
又△ABC为等边三角形,
所以FA、FB、FP两两垂直,
以F为空间直角原点,分别以FA、FB、FC所在直线为x轴、y轴、z轴建立空间直角坐标系F-xyz,如图所示.(7分)
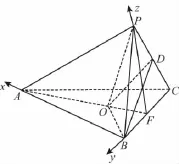

由题可知,平面PBD的法向量为m=(1,0,0),(10分)
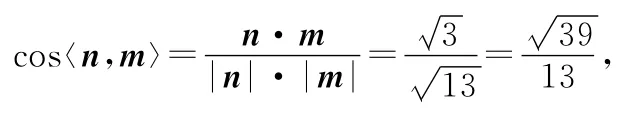
又二面角P-BD-O为钝角,即所求二面角P-BDO的余弦值为(12分)
(文)证明:(Ⅰ)取BF的中点G,连接DG、PG,
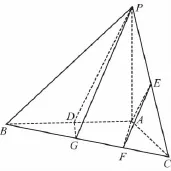
又D为AB的中点,所以DG∥AF,(2分)
又BF=2FC,所以F为GC的中点,
又E为PC的中点,所以EF∥PG,(4分)
又EF∩AF=F,所以平面PDG∥平面AEF,
所以PD∥平面AEF.(6分)
(Ⅱ)取AC的中点H,连接EH,
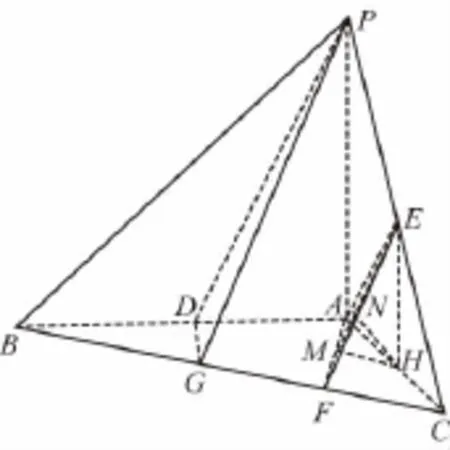
则EH⊥平面ABC,
过H作HM⊥AF于M,连接EM,
所以AF⊥平面EHM,
所以平面AEF⊥平面EHM,
过H作HN⊥EM于N,即HN⊥平面AEF,
连接AN,
则∠HAN为AC与平面AEF所成的角,(8分)




(文)解:(Ⅰ)当x≥1时,若f(x)≥a(x-1)恒成立,即
当a≤1时,g′(x)≥0,即g(x)在[1,+∞)上单增,g(x)≥g(1)=0恒成立;(3分)
当a>1时,令g′(x)=0,得x=a;
当x∈[1,a)时,g′(x)<0;当x∈(a,+∞)时,g′(x)>0;
即g(x)在[1,a)上单调递减,在(a,+∞)上单调递增,又g(1)=0,
综上所述,a的取值范围为(-∞,1].(6分)

22.证明:(Ⅰ)连接AE,
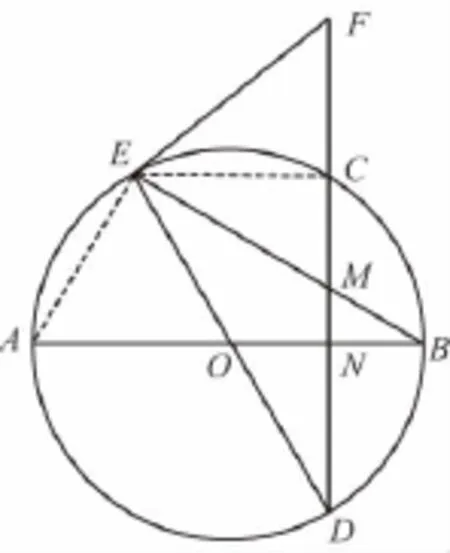
因为AB为直径,所以∠AEB=90°,又CD⊥AB,
所以A、E、M、N四点共圆,所以∠FME=∠EAB,
又EF为圆O的切线,所以∠FEB=∠EAB,
所以∠EMF=∠FEB,所以EF=FM.(5分)
(Ⅱ)连接EC,又DE为圆O的直径,
(Ⅱ)由题意可知,曲线C上的动点P与直线l上的动点Q的距离|PQ|的最小值等价于曲线C上的动点P到直线l的距离的最小值.


